一种OFDM多带联合频谱感知新算法
2015-12-18薄萍萍宫汝江
薄萍萍,宫汝江
(1.用友软件有限责任公司测试部,北京 100016;2.海军701工厂研发部,北京 100016)
频谱感知是认知无线电系统的关键技术之一。为了能给用户提供瞬时可靠的信道利用信息,其需要具备可靠检测到频谱空洞的能力[1-2]。事实上,认知系统的吞吐量和干扰量均受门限向量取值的影响,其随门限向量的变化是同增同减的关系。而一个良好的认知系统,应具有较高的吞吐量和较低的干扰量。因此,有必要根据各信道的不同情况找到合适的门限向量,在二者之间取一个折中[3-4]。目前大部分学者对频谱感知的研究并没有考虑各子信道情况,即使在对多个频带感知时,也只是将单频带上的方法逐个用到各频带上,使各频带门限值相同[5]。而在非合作频谱感知基础上引入的一种OFDM系统多带联合频谱感知是目前较为先进的前沿技术,其采用数量庞大的正交子载波,系统比单频带复杂,且计算量较大。但OFDM子载波的正交性避免了码间干扰和子载波间的干扰,且系统抗阴影和多经衰落的能力得到了增强,同时多带联合频谱感知针对各个频带的不同情况,选取各自最适宜的门限值[6],进而保证在一定干扰量下,认知系统的吞吐量达到最大。目前研究OFDM系统下多带联合频谱感知方法中门限优化问题的成果较少,其中效果较好的是基于遗传算法的多带联合频谱感知[4],但由于遗传算法易陷入局部最优、收敛速度慢等自身存在的缺陷使得优化结果不够理想。
差分进化算法(Differential Evolution,DE)是一种基于群体差异和实数编码的智能优化算法[7]。该算法具有参数少、易于实现、收敛速度快、全局寻优能力强以及良好的鲁棒性等优点,并已在函数优化、多目标问题等领域得到成功应用[8]。本文借鉴基于遗传算法的多带联合频谱感知思想,提出了一种基于差分进化算法的OFDM多带联合频谱感知方法,利用其良好的收敛特性和鲁棒性等优点及OFDM系统各子频带间的正交性,保证了在充分考虑各个正交子频带的不同情况下,寻找到各子信道最适宜的门限向量,较好解决了干扰量一定下认知系统吞吐量最大化的问题,同时改善了文献[3]提出的算法易陷入局部最优的缺点,提高了算法的收敛速度。
1 OFDM系统的多带联合频谱感知模型
OFDM技术具有抗频率选择性衰落和窄带干扰强、频谱利用率高、抵抗多径衰落好,频率选择灵活的优点,在认知无线电等许多领域得到了广泛应用,并成为频谱感知的关键技术[9],为此本文研究了OFDM系统下的多带联合频谱感知。
设系统中有一个授权用户,整个OFDM系统频带被分为N个正交子带,且该模型以能量检测为基础,则在系统N个子信道中,对于第n个子信道的能量检测模型如式(1)和式(2)所示
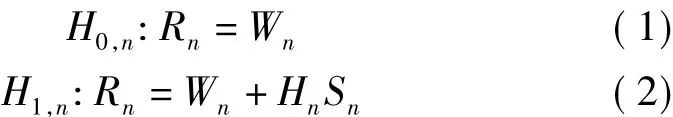
其中,Rn为第n个子信道接收信号;Wn表示均值为零、方差为1的高斯白噪声;Hn表示信道增益;Sn表示第n个子信道上主用户的发射信号;H1,n和H0,n分别表示第n个子信道有授权用户存在和有频谱空洞存在的情况,上述OFDM系统下多带联合频谱感知的模型如图1所示。
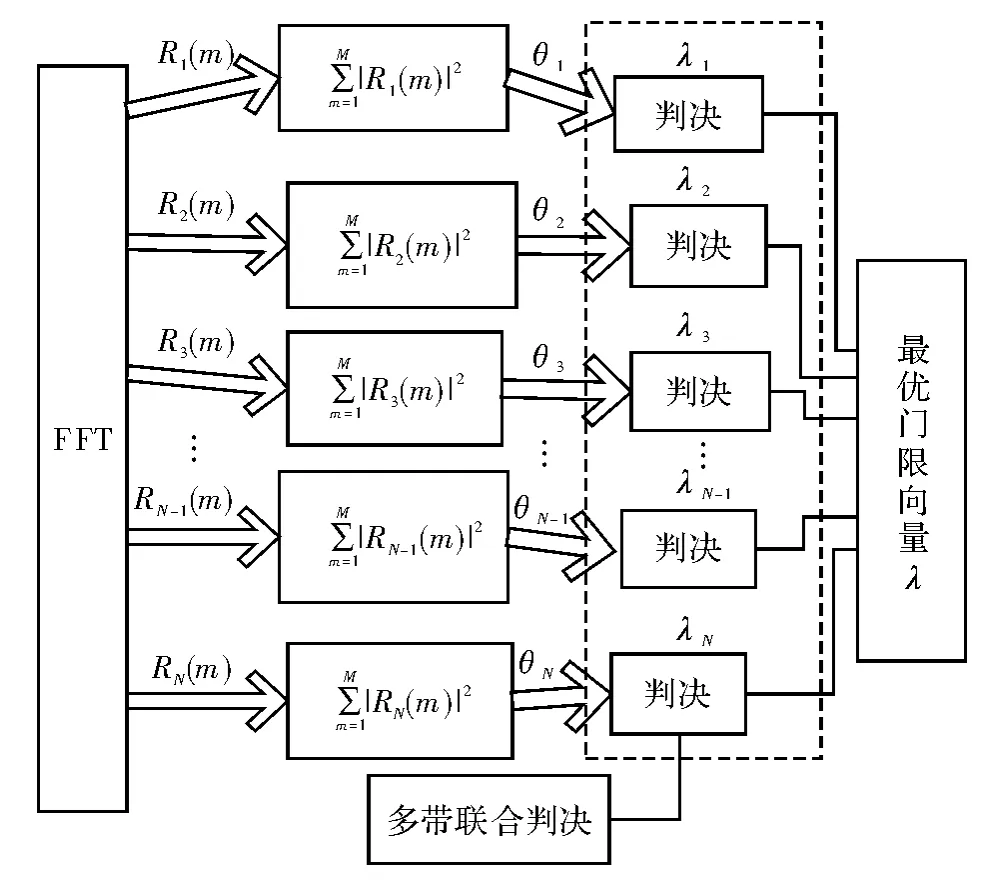
图1 OFDM系统的多带联合频谱感知模型
当对第n个子信道接收信号进行M点抽样时,接收端能量θn如式(3)所示
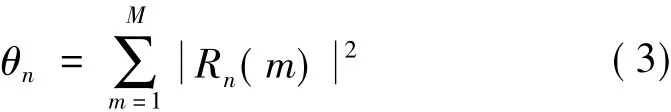
θn服从渐进正态分布,则第n个子信道上的虚警概率、检测概率和丢失概率分别如文献[4]中推导的式(4)~式(6)所示
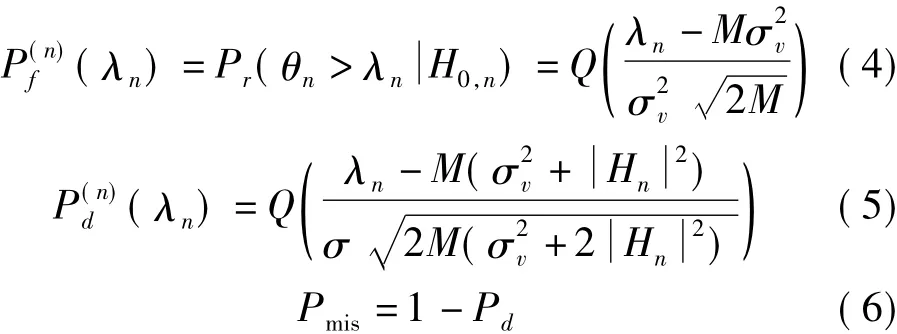
在频谱感知中,虚警概率Pf和检测概率Pd是两个重要的参量,一个良好的通信系统需要有较低的虚警概率和较高的检测概率[2]。由式(4)和式(5)可知,门限向量λn值的选取直接影响到这两个参数。较高的λn可降低Pf,提高认知系统的吞吐量,但其同时也增大了丢失概率Pmis,授权用户受到的干扰量将增大。因此,寻找合适的门限向量λ在授权用户得到充分保护的情况下,提高认知系统的吞吐量是具有研究价值的。
当认知用户机会式使用N个子信道时,认知系统获得的总吞吐量和对主用户的总干扰量分别如式(7)和式(8)所示
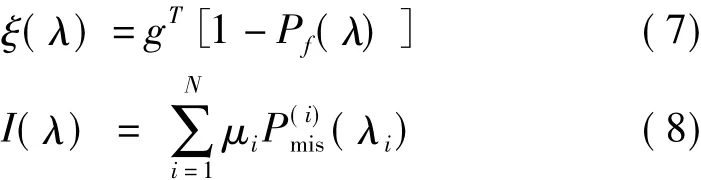
其中,μi表示由于认知用户接入在每个子信道上对主用户造成的干扰量;g(i)表示认知用户接入在第i个子信道上获得的吞吐量。
此时,寻找最优门限向量使认知系统吞吐量最大的问题,在此模型下,经公式推导可描述为
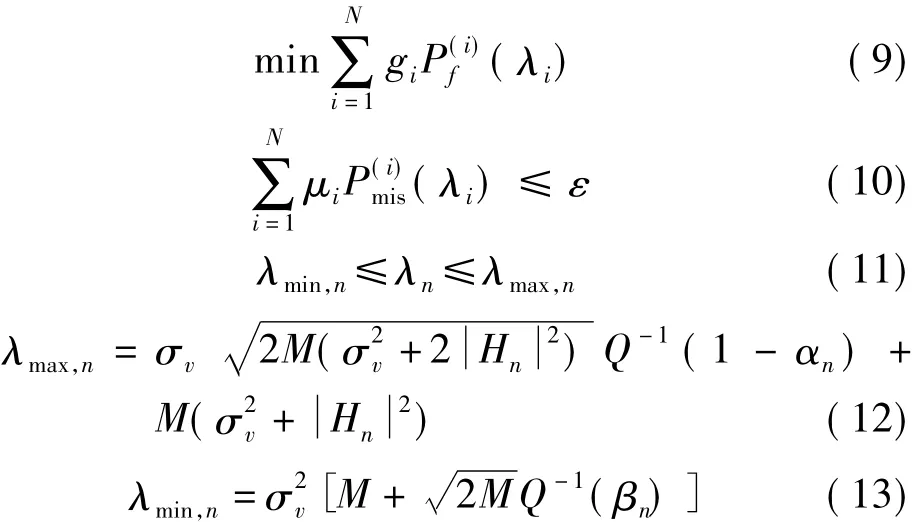
其中,n=0,1,…,N;ε 是认知系统最大总干扰量;α 为次用户对子信道最大干扰量;1-β为N个子信道应达到的最小使用率。
由于本文求解的是一个不仅有门限向量上下边界约束条件,且有一个非线性的约束条件式(10)的非线性规划问题,所以有必要引入惩罚函数,将此非线性约束优化问题变为仅受上下限约束的问题。根据本文优化问题的特点,引入的惩罚函数如式(14)所示
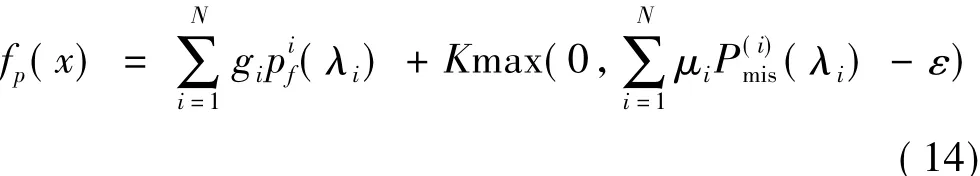
其中,K为惩罚因子,计算中取文献[4]的经验值。综合上述推导,最终将门限向量优化问题转化为如式(15)所示的寻优问题
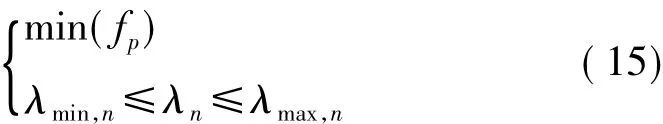
2 差分进化算法基本原理
DE算法是采用浮点矢量编码在连续空间中进行随机搜索的优化算法,相关文献已经证明DE的性能优于遗传算法和其它智能优化算法[5-6]。DE算法的基本操作有3种:变异、交叉和选择。一般先采用均匀分布的随机函数rand(·),在搜索空间可行解内随机生成pop_size个 D 维的初始种群 X=[xl,…,xi,…,xpop_size]。其中,第 i个个体表示为 xi=[xi,1,xi,2,…,xi,D]。对种群中每一个个体的基因进行变异时,先通过 randint(3,1,[1 pop_size])函数在种群中随机选择3个与之不同的个体i2,i3,i4,对其中两个个体的对应基因矢量相减后乘以权值再加到第3个个体的对应基因矢量上,即为变异操作;变异第i1个个体的第j个基因时操作式如(16)所示
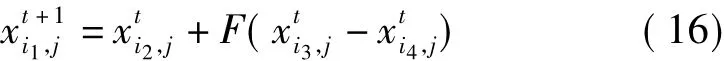
其中,F为实常数缩放因子,控制变量的放大程度,且有 i1≠i2≠i3≠i4。
然后由 randint(3,1,[1 D])随机产生一个基因序号jrand,若jrand=j,或函数rand(·)随机产生的数不大于交叉概率R,则用变异产生的新个体的基因代替父代个体的对应基因,否则父代个体该基因保持不变,此步为交叉;重复变异、交叉步骤始终到整个种群的每个个体都完成交叉,生成新的个体。然后再比较子代个体与父代个体的适应度,用较优的个体替换对应父代个体,从而产生新的种群,即为选择操作。通过变异、交叉、选择3种操作后生成的新种群作为父代种群重复上述操作,直到满足循环结束的条件,输出最优解,退出循环。差分进化算法流程如图2所示。
3 多带联合频谱感知的实现
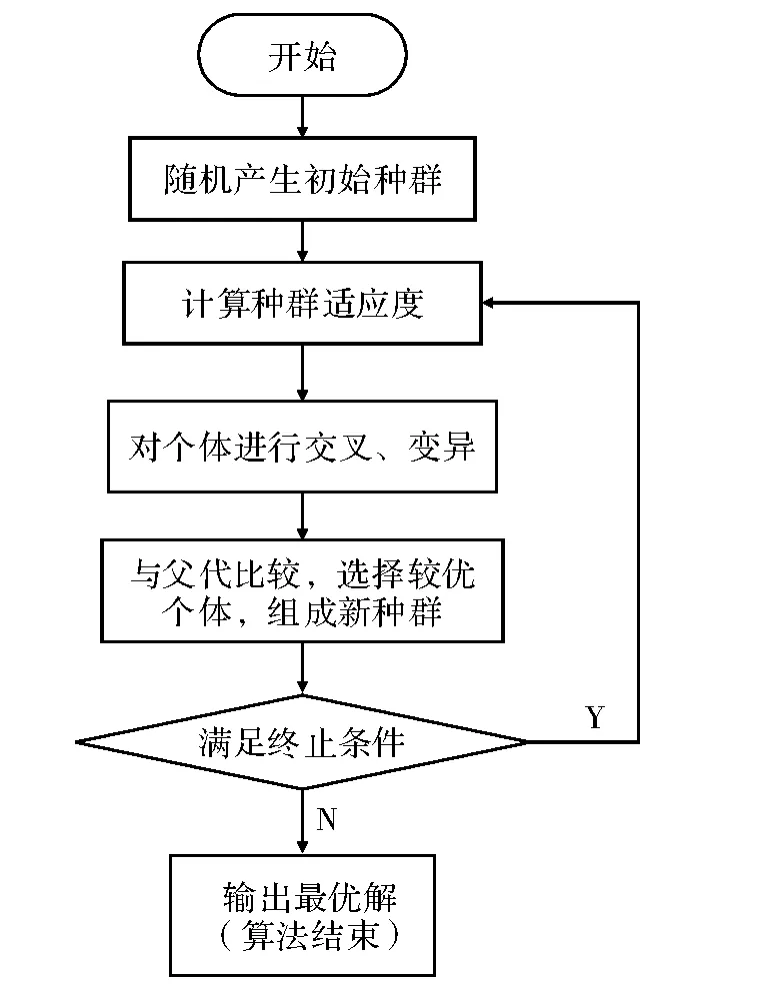
图2 DE算法流程图
OFDM系统下的多带联合频谱感知属于多载波感知,需要用到数量庞大的载波,且每个子载波都有各自的门限向量,吞吐量又是门限向量的函数,因此这是一个多维函数优化问题。为此本文利用DE算法收敛速度快、不易陷入局部最优的特点,实现了OFDM系统多带联合频谱感知中门限向量λ的优化,其具体步骤如下。
(1)种群初始化。确定种群规模pop_size,交叉概率CR,算法迭代次数,子信道数(门限向量数)D,并按照前面推导的式(12)和式(13)依次计算各个门限向量的上下限 λmax,j,λmin,j,门限向量取小数点后 4 位。再由随机函数 rand(·)随机产生初始种群 X,按式(17)依次获得种群中的每个个体
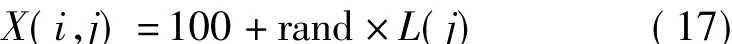
其中,L(j)为种群中每个个体第j个基因的步长,L(j)=λmax,j- λmin,j,j取值为[1,D]。
且按照适应度式(14)求出初始种群的适应度值。
(2)变异。首先确定变异因子
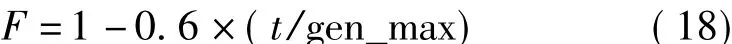
针对种群中第i1个个体的第j个基因按式(19)进行变异
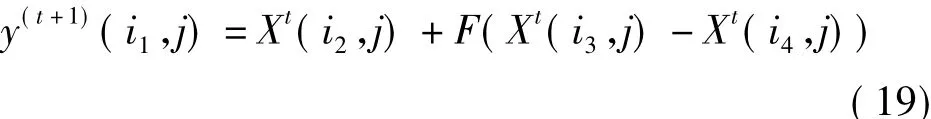
其中,变异因子F是在0.4~1之间,并随迭代次数增大而减小的变量,目的是在算法初期保持种群多样性,在算法后期加快收敛速度,向全局最优解收敛。i2,i3,i4是由 randint(3,1,[1 pop_size])生成的 3 个任意随机数,且 i1≠i2≠i3≠i4。
(3)交叉。首先将初始种群X赋值给X',对变异后第i1个个体的第j个基因进行交叉时,由randint(3,1,[1 D])随机产生一个基因序号d,如果d=j或rand≤CR(CR为交叉概率),则将X'的第i1个个体的第j个基因X'(i1,j)用变异后的基因,即式(19)中的y(t+1)(i1,j)替换。重复步骤(2)~步骤(3)直到整个种群每个个体变异、交叉结束,则产生了一个新种群X'。
(4)选择。将新产生的种群X'代入适应度函数,求出子代种群的适应度,然后与父代种群适应度做比较。如果子代X'的某个个体的适应度小于父代X的对应个体的适应度,则子代X'的该个体替换父代种群X的对应个体,最终产生新种群X,第一次迭代结束。
(5)重复步骤(2)~步骤(5),直到达到最大迭代次数,将最优门限向量带入认知系统总吞吐量式(7),最后输出最优的门限向量和对应的最大总吞吐量,算法结束。
4 实验仿真与结果分析
为验证本文提出算法的有效性和先进性,这里进行了仿真实验,并与目前解决频谱感知中门限向量优化问题效果较好的文献[3]提出的基于遗传算法的频谱感知进行了比较。仿真实验是在硬件配置为Pentium(R)Dual- Core CPU 3.19 GHz、1.96 GB 内存、3.20 GHz主频的计算机上运行。主程序采用Matlab 7.0版本编写。

本实验从限定干扰量下认知系统总吞吐量和运行时间两个角度来验证了基于差分进化算法的频谱感知的收敛精度及收敛速度。基于差分进化算法的OFDM系统多带联合频谱感知所得的优化门限向量具体数据如表1所示,认知系统总吞吐量的对比实验仿真结果如图3所示,实验仿真得到的两种优化算法的收敛速度如图4所示。
图3为在充分考虑各子信道情况下,在一定的干扰限制时,DE算法和遗传算法关于系统总吞吐量的仿真对比。从图3可看出,在系统总干扰量相同的情况下,用本文的DE算法优化门限向量所得到的认知系统总吞吐量远大于用遗传算法所得到的;且当认知系统总吞吐量相同时,DE算法对授权用户产生的总干扰量,也远小于遗传算法产生的干扰量,由此说明本文提出算法所获得的门限向量优化效果较好,具有一定的先进性。
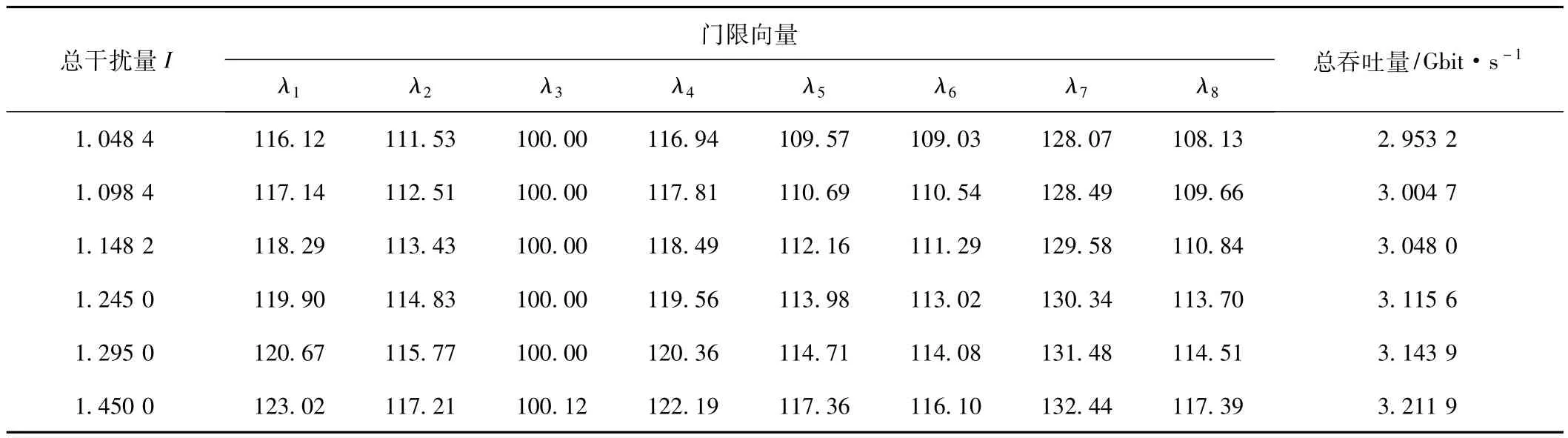
表1 基于差分进化算法在不同总干扰量情况下的最优门限向量值和总吞吐量
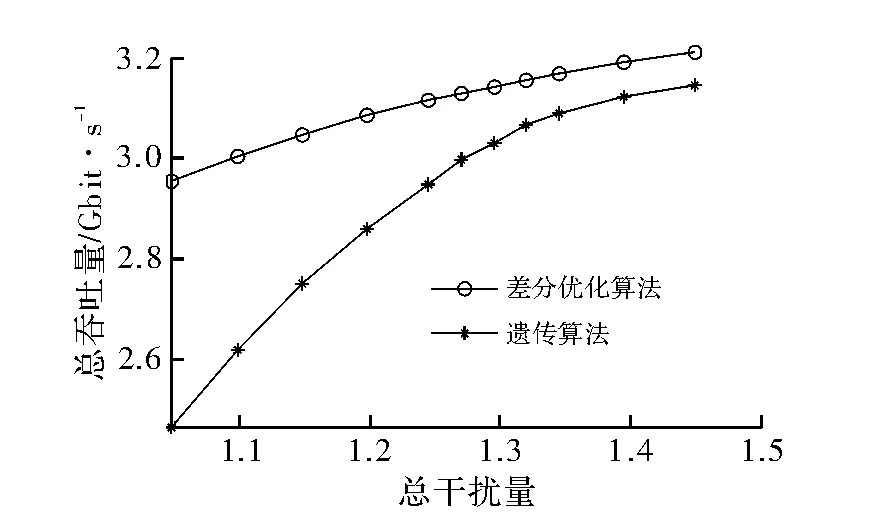
图3 差分进化算法与遗传算法吞吐量仿真结果比较
图4所示,在若干相同的总干扰量下,寻找到最佳门限向量,吞吐量达到最大时,两种优化算法的收敛情况对比,由此图可知,差分进化算法的收敛时间远少于遗传算法的收敛时间。
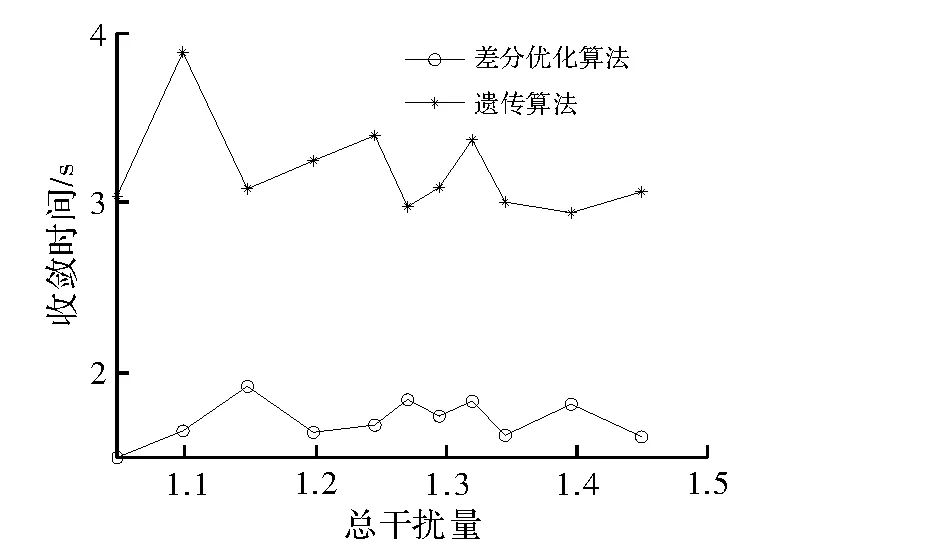
图4 基于差分进化算法和遗传算法的收敛速度比较
总之,通过两方面的仿真实验可看出,本文提出的算法无论是在收敛精度还是收敛速度方面均具有较大优势。
5 结束语
本文将差分进化算法引入OFDM系统下的多带频谱感知中,利用差分进化具有收敛速度快、全局搜索能力强、控制参数少等优点实现了门限向量的最优选取。从实验仿真结果可看出,本文提出的差分进化算法能在充分考虑各个信道的情况下,寻找到最优的门限向量,使授权用户得到较好保护的条件下,认知系统的吞吐量达到最大,同时提高了算法收敛速度,在通信系统中具有一定的应用价值。
[1] 薛峰.认知无线电系统频谱感知技术研究[D].武汉:华中科技大学,2010.
[2] Haykin S.Cognitive radio:brain - empowered wireless communications[J].IEEE Journal on Selected Areas in Communications,2005,23(2):201 -220.
[3] 邓丽粼,张翠芳,周兴建,等.遗传算法在认知无线电频谱感知中的应用[J].通信与网络,2010(3):113-116.
[4] Digham F F,Alouini M S,Simon M K.On the energy detection of unknown signals over fading channels[J].IEEE Transactions on Communications,2007,55(1):21 -24.
[5] Quan Zhi,Cui Shuguang,Vincent Poor H,et al.Collaborative wideband sensing for cognitive radios[J].IEEE Signal Processing Magazine,2008,25(6):60 -73.
[6] 毕晓君,王义新.多模态函数优化的拥挤差分进化算法[J].哈尔滨工程大学学报,2011,32(2):223 -227.
[8] 毕晓君,肖婧.差分进化算法GVF Snake模型 在PET图像分割中的应用[J].中国图象图形学报,2011,16(3):382-388.
[9] 包路平,张元.OFDM技术在认知无线电中应用的研究[J].西安邮电学院学报,2007,12(5):54 -57.
