多小区MIMO系统中干扰对齐算法分析

刘 允

(中国电子科技集团公司第54研究所通信网信息传输与分发技术国家级重点实验室，北京 100071)

多输入多输出(Multiple－Input Multiple－Output，MIMO)以及Massive MIMO技术由于能显著提高频谱利用率和系统吞吐量，被公认为下一代移动通信的关键物理层技术之一［1］。同频组网方式下，小区间的干扰会严重削弱MIMO技术的高频谱效率优势。因此，在多小区MIMO系统中如何有效抑制小区间干扰，提高边缘用户的吞吐量成为了研究热点［2－3］。

干扰对齐技术作为协作多点传输(COMP)中有效的干扰管理方法，为解决上述问题提供了一种新思路。目前，针对干扰对齐技术的研究重点集中在多小区MIMO系统，其算法主要有两种:一种是基于求闭式解的经典干扰对齐算法［4－7］;另一种是分布式的迭代干扰对齐算法［8－11］。本文主要对这两类典型算法进行了分析。

基于工程应用的需求，重点对求闭式解的经典算法、基于最小化干扰泄露、最大化信干噪比以及基于矩阵投影的分布式迭代经典算法，在系统容量及算法收敛性等方面的性能进行了分析比较;同时，考虑到未来Massive MIMO技术的应用使得空间无线信道不再相互独立，进一步分析了各算法在相关信道下的性能;最终，针对各算法的特点，分析总结了其相应的适用情况，对干扰对齐技术在协作通信系统的实际应用具有指导意义。

1 系统模型

本文研究的多小区MIMO系统可建模为K用户干扰信道模型，如图1所示。即每个接收机除了收到自身对应发射机发送的信号外，同时还收到其他发射机发送的干扰信号。

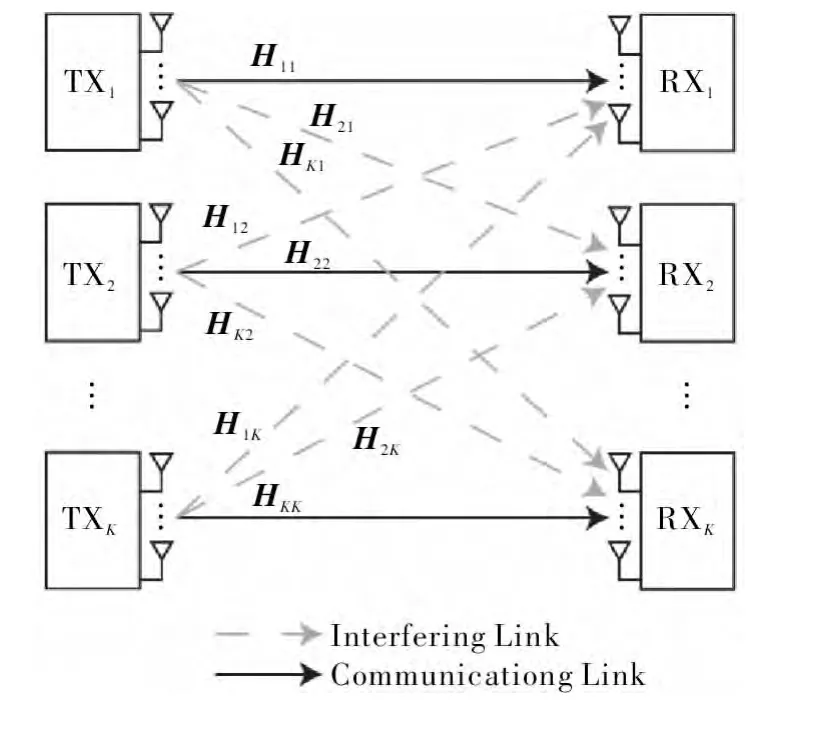
图1 K用户干扰信道模型

则第k个接收端收到的信号可表示为

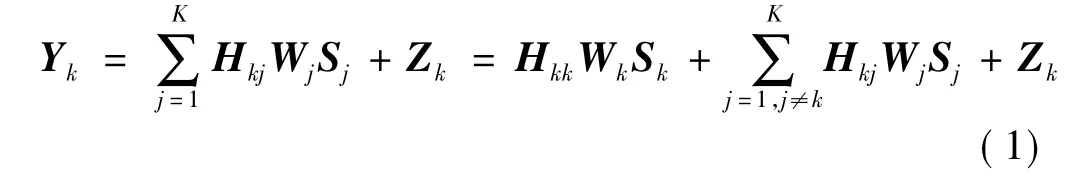
其中，第一项为期望收到的有用信号，第二项为其他发射端产生的干扰信号，最后一项为归一化复高斯信道噪声。Sj，j=1，2，…，K 为第 j个发射端发送的 dk×1维信号矢量;dk为第k个收发机之间独立传输的数据流个数;Wj表示发射端预编码矩阵;Hkj表示从发射机j到接收机k的信道矩阵。

干扰对齐技术可将多个用户的干扰降低为单一用户的干扰，使系统获得最优的自由度。在其实现算法中，关键是预编码矩阵的设计实现。该技术的目标就是通过对所有发射端预编码矩阵{Wj}Kj=1的协同设计，使接收机将干扰信号对齐到同一子空间，并通过干扰抑制矩阵对干扰迫零，获取期望信号。干扰对齐实际上就是将干扰信道转化为多个并行的无干扰高斯信道。

2 多小区MIMO系统干扰对齐技术

2.1 求闭式解的经典干扰对齐算法

干扰对齐技术实现的关键是发射端预编码矩阵的设计，文献［4］中给出了基于求闭式解的经典干扰对齐算法的实现。简单起见，以K=3，M=N且为偶数为例来介绍各类典型干扰对齐算法的实现对每个用户要实现干扰对齐，即将来自另外两个用户的干扰对齐到相同的子空间内，则发射端预编码矩阵必须满足如下条件

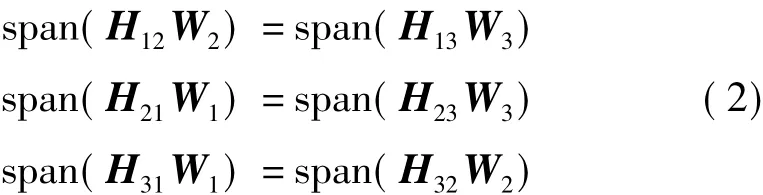
其中，span(A)代表由矩阵A的列向量所张成的空间。上述条件可简化为

从以上算法实现过程可看出，基于求闭式解的经典干扰对齐算法需了解全局理想信道状态信息(Channel State Information，CSI)，适用于有中心控制节点的多小区MIMO系统，例如蜂窝系统中基于基站控制实现的Device To Device业务。

2.2 分布式干扰对齐算法

基于求闭式解的经典干扰对齐算法需了解CSI，如何在只知本地信道状态信息的前提下实现干扰对齐成为一个难点;同时，随着用户数K的增加，干扰对齐实现的约束关系也会随之增加，尤其是当用户数K＞3时，MIMO系统中干扰对齐算法无法获得预编码矩阵的确知解。基于此，学者们提出了分布式迭代实现的干扰对齐算法，比较典型的有依赖于信道互易性(对偶性)实现的迭代算法以及基于矩阵投影距离的迭代算法。

2.2.1 分布式迭代干扰对齐算法

文献［8］利用上下行信道的互易性解决干扰对齐的可行性问题，给出了一种分布式的干扰对齐技术的实现方法。

在接收端，信号经干扰抑制滤波器后仍残留在期望信号空间内的干扰信号功率定义为该接收端总的干扰泄露，则在原网络接收端i，其他发送端对其总的干扰泄露可表示为

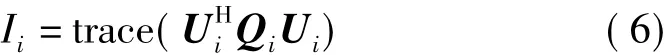
其中，Qi是接收端i的干扰协方差矩阵，即

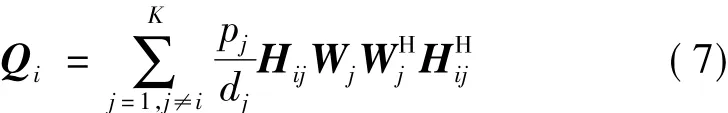
所有接收端干扰泄露之和为

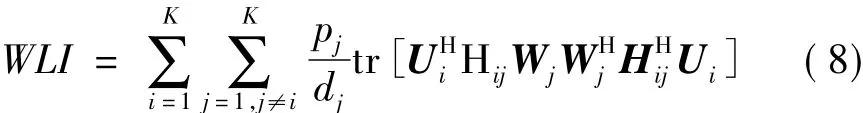
用户i为了获得最小的干扰泄露，接收矩阵设计为

上述两种分布式干扰对齐算法放宽了对CSI的要求，只需了解本地信道状态信息，实现的关键是传输信道必须“互逆”，只适合于TDD系统，例如TD－LTE(Time Division－Long Term Evolution)系统。2.2.2 基于矩阵投影距离的干扰对齐算法

针对基于信道互易性的分布式迭代干扰对齐算法仅适用于TDD系统的局限性，文献［10］提出了一种基于矩阵投影距离的干扰对齐预编码算法，该算法首先假设发射端预编码矩阵已知，优化接收端干扰抑制矩阵，优化目标函数如下

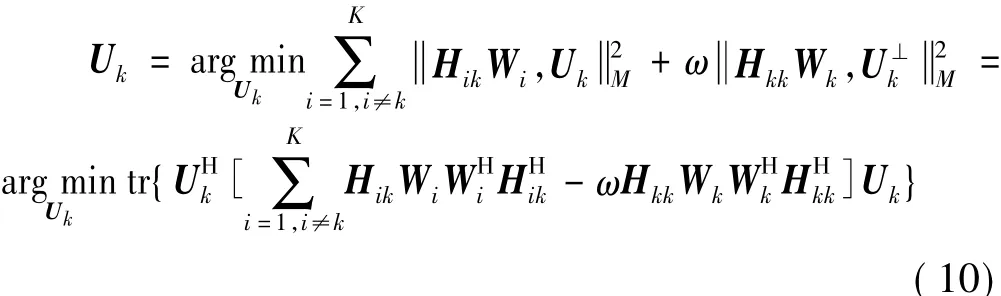
同理，发送端预编码矩阵优化目标函数为

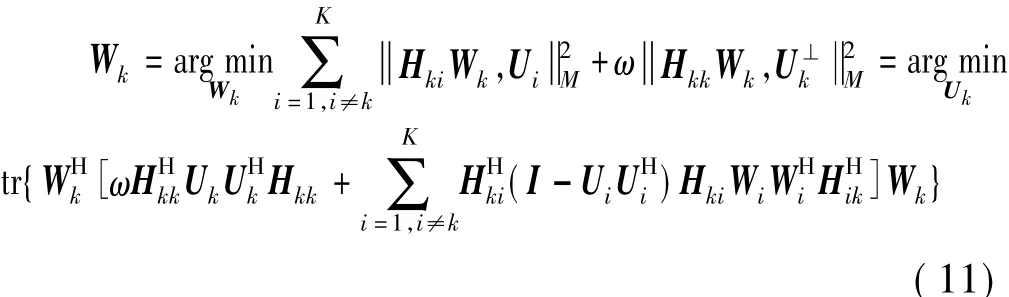
其中，第一项代表第k个发射端用户泄露到其他接收端的能量，即对其他用户端的干扰;第二项代表第k个发射端用户泄漏到第k个接收端正交方向的能量。

基于矩阵投影联合优化干扰和信号的算法，以同时最小化干扰泄露功率以及有用信号到其正交补空间的功率为目标，实现了对发射端预编码矩阵和干扰抑制矩阵的优化设计。该算法不依赖信道互易性条件，使其适用范围从TDD系统扩展到FDD系统。

3 仿真分析

为了分析各算法的性能及适用性，对基于求闭式解的经典干扰对齐算法(CJ－IA)、最小化干扰泄露算法(Min_WLI)，最大化信干噪比算法(Max_SINR)以及基于矩阵投影距离的干扰对齐(Hyb_Sig_Infer)等算法的性能进行了仿真分析。在仿真中，采用K=3个小区;基站和用户均配置2根天线;所有的信道均是独立同分布的瑞利信道，且服从0均值方差为1的复高斯分布;每个基站均满足功率受限条件，且采用功率均分方案。仿真结果如图2和图3所示。

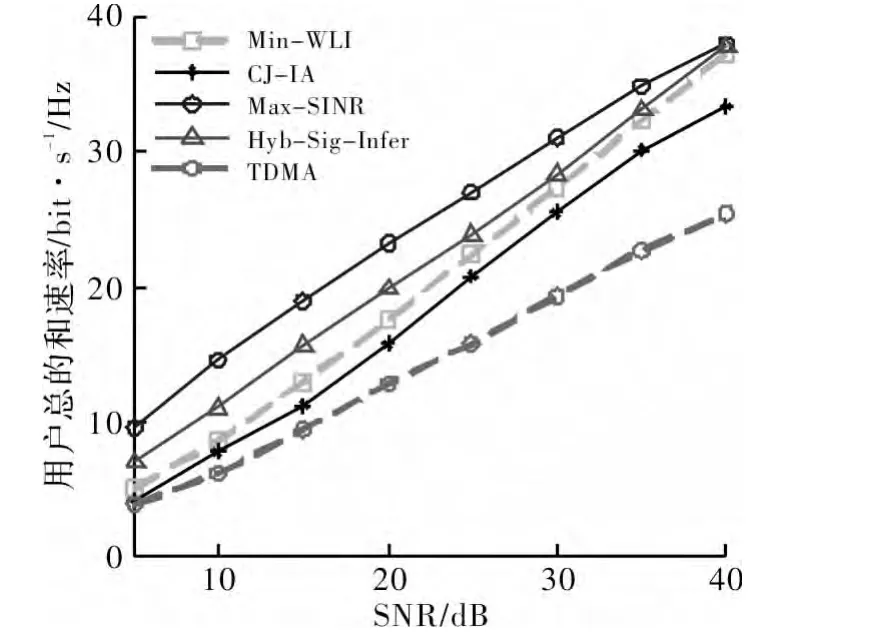
图2 不同干扰对齐算法及TDMA传输吞吐量比较

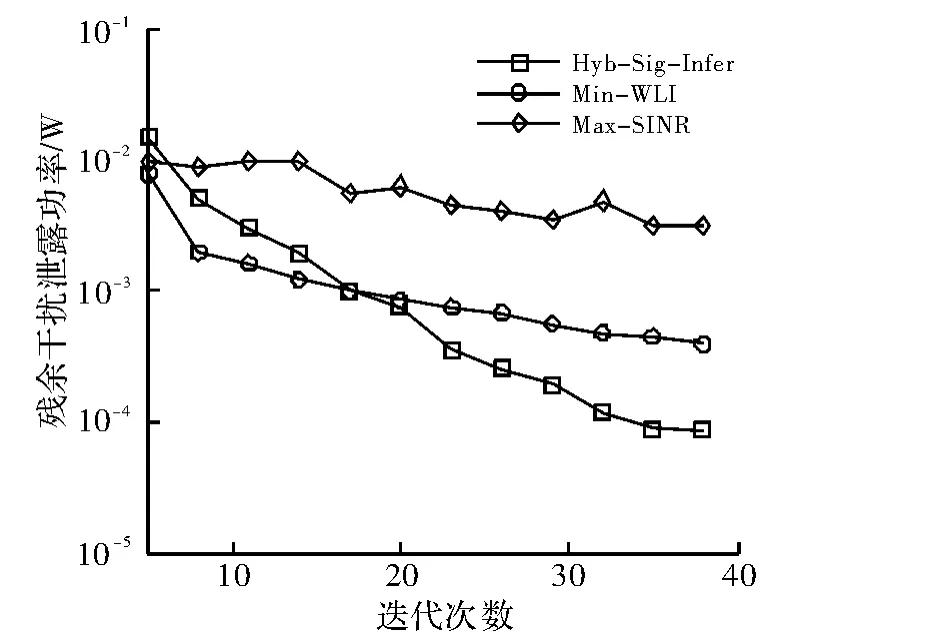
图3 3种迭代算法的收敛性比较

首先，图2给出了各算法的系统容量(和速率)比较曲线，并对MIMO－TDMA系统的容量性能进行了仿真对比。从图中可看出，各类干扰对齐算法的性能明显优于MIMO－TDMA传输系统;CJ－IA算法的性能明显低于其他干扰对齐算法，这是由于其接收端干扰抑制滤波器采用简单的迫零矩阵同时损失了有用信号的功率;在中低信噪比条件下，3种迭代算法中Hyb_Sig_Infer的性能明显优于Min_WL算法，这是由于该迭代算法不仅最小化了泄漏到干扰子空间的信号能量，且同时也最小化了泄漏到信道子空间自身的干扰信号能量。

其次，为了比较Min_WLI、Max_SINR及Hyb_Sig_Infer的3种迭代算法性能，图3给出了3种算法的收敛性比较曲线。纵坐标代表有用信号空间中归一化后的干扰信号强度，理论上干扰对齐实现后，干扰信号强度趋于0。从图中可看出，Hyb_Sig_Infer算法的收敛性最佳，Max_SINR算法则难以收敛，这是由于Max_SINR算法实现过程中SINR非线性导致的。

多天线场景下尤其是未来Massive MIMO场景下，受天线尺寸和密度等限制使得无线空间信道存在一定的相关性。而目前干扰对齐算法在相关信道下性能研究较少，考虑未来工程实现的需求，本文同时对算法在空间相关信道下的性能进行了仿真比较，如图4所示。从图中可看出，相对于其他干扰对齐算法，Hyb_Sig_Infer算法性能最优，对相关信道具有更强的鲁棒性。

图4 相关信道下，算法吞吐量随相关系数变化的比较曲线

对比图2～图4可知，虽然Max_SINR算法在提高系统容量方面具有明显优势，但其不易收敛，实际工程中难以应用;而Hyb_Sig_Infer算法在系统容量方面的性能仅次于Max_SINR算法，且具有较好的收敛性，对相关信道也具有良好的适应性，同时该算法还避免了对“信道互逆性的”及中心控制节点的依赖，同时适用于FDD系统和TDD系统。综上所述，Hyb_Sig_Infer算法整体性能最优，且具有最佳的工程适用性。

4 结束语

干扰对齐技术因其自由度和提高系统性能等方面的优势，必将被广泛应用于未来的MIMO系统中，以改善小区边缘用户的性能，提高信道容量。因此，本文重点研究了多小区MIMO系统中干扰对齐技术的实现，对各类典型算法在系统容量及算法收敛性等方面的性能进行了分析比较;同时，考虑目前干扰对齐算法均是基于空间信道相互独立的条件下实现的，针对未来Massive MIMO技术的应用需求，进一步对各类典型算法在相关信道下的性能进行了仿真分析。结果表明，基于矩阵投影距离的干扰对齐算法综合性能最优，具有良好的工程适用性。最后，针对各类算法的特点及性能，分析总结了其相应的适用情况，为干扰对齐技术未来的工程实现提供参考，亦对其在协作通信系统的实际应用有着指导意义。

［1］ 尤肖虎，潘志文，高西奇，等．5G移动通信发展趋势与若干关键技术［J］．中国科学:信息科学，2014，44(5):551 －563．

［2］ Ruan L，Lau V K N，Win M Z．The feasibility conditions for interference alignment in MIMO networks［J］．IEEE Transactions on Signal Processing，2013，61(8):2066 －2077．

［3］ Huang C，Jafar S A，Shamai S，et al．On degrees of freedom region of MIMO networks without channel state information at transmitters［J］．IEEE Transactions on Information Theory，2012，58(2):849 －857．

［4］ Cadambe V R，Jafar S A．Interference alignment and the degrees of freedom for the K user interference channel［J］．IEEE Transactions on Information Theory，2008，54(8):3425－3441．

［5］ 徐冰，谢显中，马彬，等．MIMO干扰信道下的协作干扰对齐优化算法［J］．信号处理，2012，28(2):220 －225．

［6］ Shin W，Lee N，Lim J B，et al．On the design of interference alignment scheme for two－cell MIMO interfering broadcast channels［J］．IEEE Transactions on Wireless Communications，2011，10(2):437 －442．

［7］ Suh C，Ho M，Tse D．Downlink interference alignment［J］．IEEE Transactions on Communications，2011，59(9):2616 －2626．

［8］ Gomadam K S，Cadambe V R，Jafar S A．Approaching the capacity of wireless networks through distributed interference alignment［C］．IEEE Global Telecommunications Conference(GLOBECOM)，2008:1 －6．

［9］ Peters S W，Heath Jr R W．Interference alignment via alternating minimization［C］．IEEE International Conference on Acoustics，Speech and Signal Processing，2009:2445 －2448．

［10］ Kumar K R，Xue F．An iterative algorithm for joint signal and interference alignment［C］．Austin Texas，USA:2010 IEEE International Symposium on Information Theory Proceedings(ISIT)，2010:2293 －2297．

［11］ Gomadam K S，Cadambe V R，Jafar S A．A distributed numerical approach to interference alignment and applications to wireless interference networks［J］．IEEE Transactions on Information Theory，2011，57(6):3309 －3322．