基于遗传算法的随机脉位多普勒引信波形优化
2015-12-18苏宇逍
苏宇逍
(中国空空导弹研究院总体部,河南洛阳 471009)
随着作战环境的日趋复杂,无线电引信抗干扰设计面临着日益严峻的挑战。引信发射波形的设计和选择较大程度上决定了引信的探测性能、抗干扰性能以及接收机形式[1-2]。增加发射特征参数、减小引信信号截获概率、提高速度、距离分辨率以及增强从干扰中检测出目标回波的能力是波形设计的主要任务。随机脉位调制的脉冲多普勒引信是一种先进且被广泛采用的引信体制,通过使脉冲重复周期随机变化,即脉位变化,使敌方难以侦收和转发,从而提高其抗干扰能力。同时,该体制可有效抑制距离副瓣,当脉位调制范围足够大时,其模糊函数图呈近似图钉形,具有高距离、速度分辨率和低副瓣,可显著提高引信的超低空工作性能。在随机脉位波形设计中,涉及到脉冲重复周期、随机调制范围、随机数分布特征等诸多参数的选择,如何协调选择参数,以得到最优的模糊函数是设计的主要内容。在以往的该体制波形设计中,仅利用某种伪随机数实现了脉冲位置的随机变化,未对不同码型之间的性能差异进行充分的分析,本文对其抗干扰性能和距离副瓣抑制效果进行了分析,并根据需要进行进一步的优化,使得该体制的优势能充分发挥。
遗传算法作为仿生学的成果,是基于进化论和自然选择的数学抽象,广泛应用于科学计算的其他领域。其具有智能式搜索、渐进式优化、并行式计算及全局最优化等特点,适用于目标函数为多特征参数、多极值的最优解搜索[3-4]。本文以波形的模糊函数[5]作为目标函数,利用遗传算法高效地搜索全局的最优解,实现了发射波形的优化设计。
1 随机脉位信号的产生
随机脉位调制的信号,其调制波形数学表达式可由式(1)表示[6]
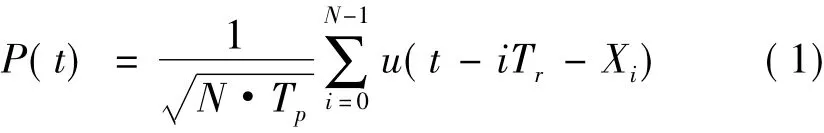
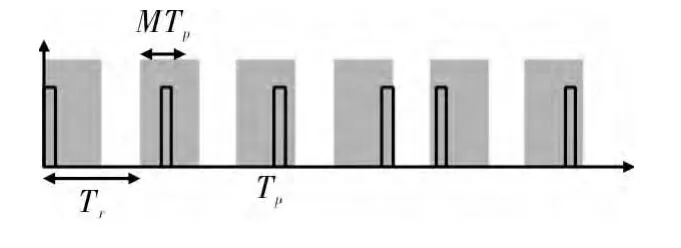
图1 随机脉位脉冲序列波形图
1.1 随机数的产生
用于调制脉冲位置的随机数的产生有多种方法,本文采用线性反馈移位寄存器产生的最长周期序列作为随机数产生的基础。根据调制范围M的大小取最长周期序列即m序列中的若干位,转换成十进制数后,即可产生在[0,M]范围内服从均匀分布的一组随机数Xi作为脉位调制数。图2所示为随机数产生原理框图。
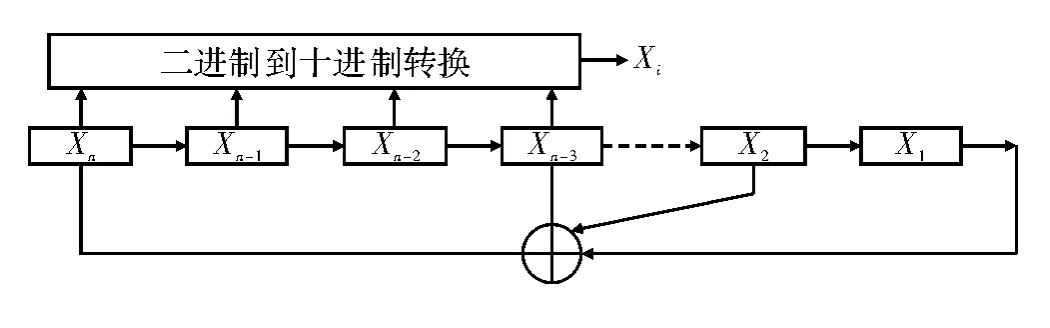
图2 随机数产生原理框图
m序列是一种伪随机序列,其是按照完全确定的规律产生并且具有类似于随机序列所具有的随机特性的二元序列。由级线性反馈移位寄存器产生的m序列最大周期为2n-1。利用m序列产生脉位调制随机数,经调制后的序列或波形具有伪随机特征,随着序列长度的增加,其随机特征更加明显。
m序列参数的选择不仅影响脉冲序列的自相关函数,同时也影响最终发射波形的模糊函数。线性反馈移位寄存器级数n、寄存器初值{xi}及反馈连接即反馈多项式均可作为待优化的参数。
1.2 模糊函数
模糊函数及自相关函数是对雷达信号进行分析研究和波形设计的有效方法。模糊函数将雷达接收机输出信号的复包络描述为雷达目标距离和径向速度的函数,其较直观地说明了发射信号及信号处理系统对距离、速度分辨率、抗干扰能力以及引信的多普勒容限等重要参数。
设发射信号为P(t),回波在发射信号的基础上产生一时间延迟τ和多普勒频移fd,在接收滤波器为匹配滤波器时,其输出信号的复调制即为模糊函数
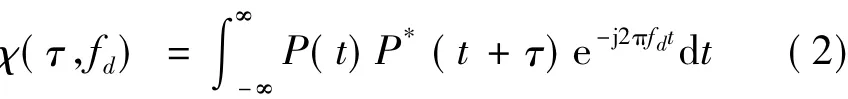
式中,P*(t)是P(t)的复共轭函数。
当fd=0时,上式变为
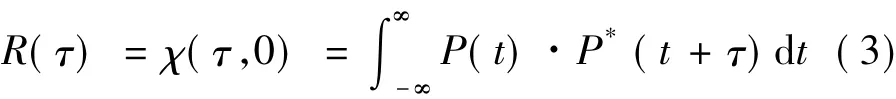
即自相关函数,亦称距离模糊函数,其表明了信号与自身的相互关联程度。由式(3),可推导出式(1)表示的脉冲序列信号的模糊函数为[4]
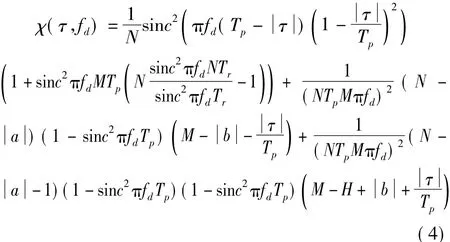
式中,H=Tr/Tp;a,b可表示为 τ=aTr+bTp+ τ',即将τ量化为Tr的整数倍a,再将余量量化为Tp的整数倍b,余量用 τ'表示,0≤ τ'≤Tp,a和b为整数且同号。
2 应用遗传算法进行优化
遗传算法是对自然进化论的类比与数学抽象。其通过编码,利用再生、交叉、变异等基本算子,以迭代、自适应、启发式的随机搜索算法在点群中进行全局寻优。遗传算法包括参数编码、初始群体确定、适应度函数的确定、遗传操作设计、进程控制参数设定5个基本要素。本文以线性反馈移位寄存器初值作为参数编码个体,由不同反馈多项式及初值为基础产生初始种群。
2.1 适应度计算
以脉位调制序列的平均模糊函数即式(4)作为优化的目标函数,以距离及速度自相关函数的主副瓣比、等高剖面图的面积大小作为判断个体优劣的依据,对不同次迭代得到的个体进行适应度计算。适应度为距离自相关函数的主副瓣比和等高剖面图的面积,主副瓣比及等高剖面图的面积越小,则个体越优秀,相应的适应度则越高,个体被复制的可能性也应越大,所以个体被复制的概率及用于交叉的概率Pc就越大。
平均模糊函数在距离轴或速度轴的主副瓣比越大,表明引信的距离或者速度分辨率越高,其表明了引信在低空环境或者干扰存在的情况下作战性能。根据雷达抗干扰性能评估的功率准则,模糊函数的等高剖面图的面积可表明抗各种干扰的能力。以此为依据计算每次迭代得到的个体的适应度,根据适应度大小确定个体被复制、交叉的概率,可以的将群体中强壮个体的全部或部分遗传物质传递给下一代,使健壮个体得到指数增长的再生机会。
复制或者交叉可将父代优良的性能传递到下一代,使子代具有优于父代的性能。但当交叉产生的后代不如父代好时,会发生早熟收敛。变异可有效防止早熟的发生,其具体操作是随机的对群体中个体基因位上一个或多个基因位加以改变。改变的概率称为变异概率Pm。变异能产生新的个体,增加了全局优化的特质。本文采用单点变异方式,对反馈位进行变异。
2.2 进程控制参数的选取
遗传算法的进程控制参数包括:群体规模n、编码长度l、交叉概率Pc和变异概率Pm等。这些参数均从不同程度上影响着算法的进程。
种群规模过小易造成最优个体的丢失、强壮个体的过度支配等作用,从而会导致早熟。而种群规模过大会是适应度计算的运算量变大。个体适应度较大时,交叉概率Pc若设置过高,会造成强壮个体的过度支配而导致算法早熟收敛。变异概率Pc设置过大将是优秀的遗传信息丢失,造成算法过早收敛或无法找到最优解。综合以上考虑因素,参数选取n=5,Pc=0.55,Pm=0.03。
2.3 程序流程图
算法以Gen表示迭代次数,即种群的进化次数。综合考虑计算量及计算时间,以50次为算法终止条件。由初始值经递归反馈得到初始种群,在进化次数到达之前,循环计算个体的模糊函数,得到个体的适应度,再由此确定交叉复制概率Pc及变异概率Pm。在原始种群中依概率对个体进行复制、交叉及变异,得到新的个体并添加到新的种群中。当迭代次数满足要求是输出适应度最大的个体。优化程序流程图如图3所示。

图3 程序流程图
2.4 优化结果对比
图4中左列为参数优化前波形的模糊函数三维图、等高剖面图及距离自相关函数图,右列为优化后的结果。
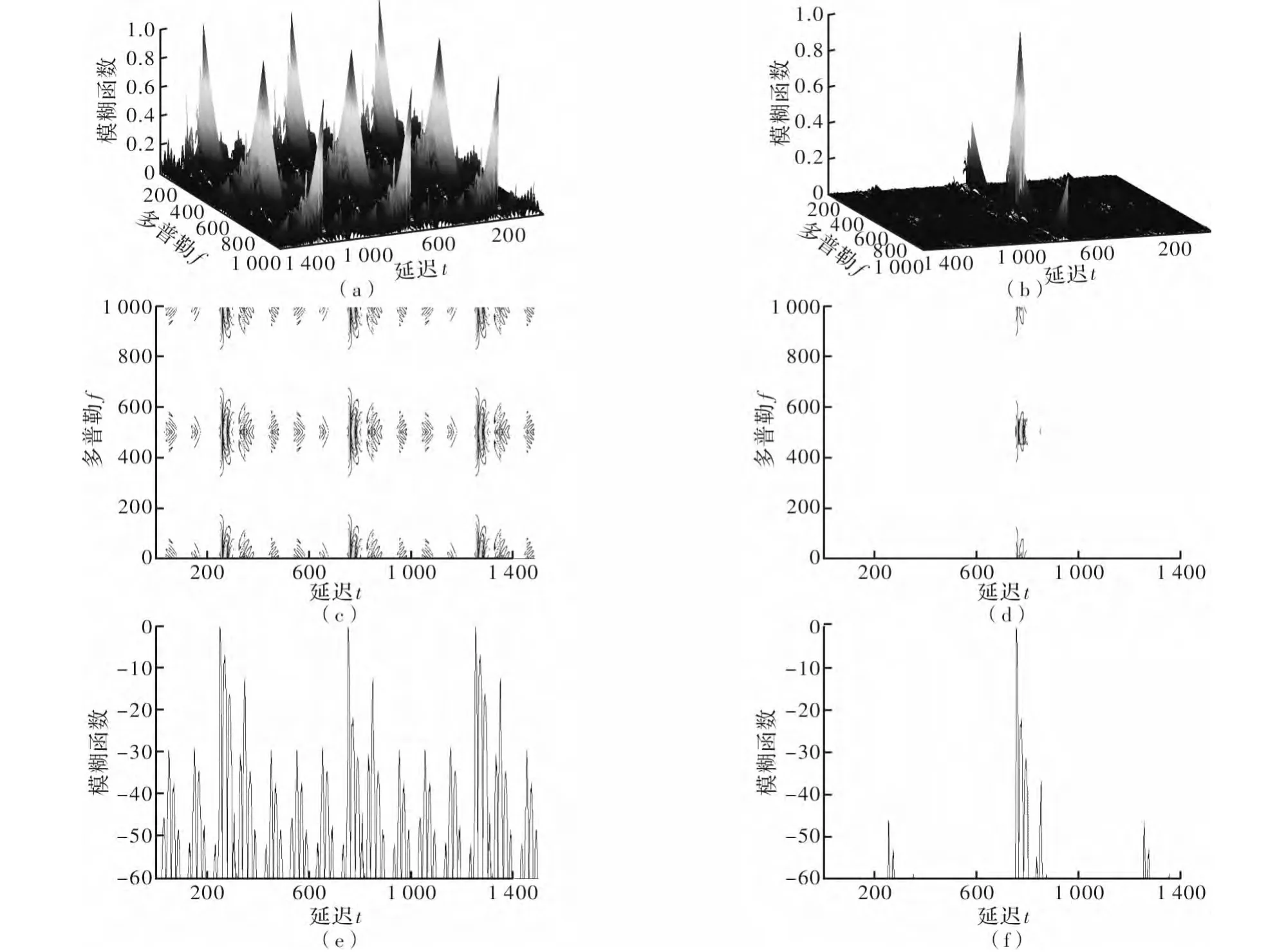
图4 优化结果对比图
3 结束语
采用遗传算法优化的方法,对随机脉位体制引信的波形进行优化设计,优化参数包括寄存器初值及反馈多项式。选择不同初值及反馈多项式可得到不同的波形模糊函数,优化后的引信模糊函数图表明,该制的引信可较好地消除距离及速度模糊,其模糊图跟接近图钉型,有较尖锐的主峰。这种方法为引信波形设计的参数寻优提供了一种高效、实用的工程手段,可使波形设计达到最佳。同时,该方法还能以脉冲宽度、重复频率及调制范围等参数作为优化对象,对波形设计进行系统优化,以达到更好的效果,并可进一步发挥该体制引信的抗干扰优势。
[1] 赵国庆.雷达对抗原理[M]西安:西安电子科技大学出版社,1999.
[2] 杜汉卿.无线电引信抗干扰原理[M].北京:兵器工业出版社,1988.
[3] 张文修,梁怡编.遗传算法的数学基础[M].西安:西安交通大学出版社,1999.
[4] 吴龙,任红民,毕惟红.遗传算法求解非线性方程组研究综述[J].电子科技,2014,27(4):173 -178.
[5] 戴伟倩.MIMO 雷达性能分析[J].电子科技,2009,22(10):56 -59,81.
[6] 丁庆海,陆锦辉,是湘全,等.随机脉位调制脉冲串雷达信号的平均模糊函数[J].电子学报,1997(12):89-91.
