融合多传感信息的仿人机器人姿态解算

2015-12-18毕俊熹娄小平祝连庆

电子科技 2015年1期

谢宁，毕俊熹，娄小平，祝连庆

(1.北京信息科技大学仪器科学与光电工程学院，北京 100192;2.北京信息科技大学光电测试技术北京市重点实验室，北京 100192)

RoboCup Soccer为仿人机器人研究领域提出了一系列标准问题，并逐渐成为人工智能学和机器人学的研究热点。在各种相关问题中，机体的姿态解算是其中的基本技术之一。仿人机器人姿态解算的实质是融合机体内多传感信息经姿态解算单元以欧拉角形式正确输出的机体实时姿态角。

自1997年RoboCup首届比赛以来，该领域已取得了一系列研究成果，各组别机器人均有了相对稳定、成熟的硬件平台和姿态解算算法。文献［1］分析了单种惯性器件测量的原理和精度，文献［2］提出了一种基于加速度计和陀螺仪的倾角检测方法，同时借助视觉中的颜色信息以算法的手段得到近似的机体姿态信息。随着仿人机器人技术的逐渐发展，RoboCup的要求越来越高，目前已取消场地陆标及球门颜色差异，现有的基于倾角计和场地陆标的姿态解算算法已不适用于最新的RoboCup比赛规则。故本文在原有算法的基础上，以自主姿态测量为前提，提出了一种基于惯性测量单元的四元数法姿态解算。

1 传感器数据融合

本文采用惯性测量单元(Inertial Measurement Unit，IMU)GY－80作为姿态传感器，包括三轴加速度计、三轴陀螺仪、三轴磁强计等，工作时水平固定在机体上。

IMU测量精度的真正参考来自于加速度计对地球重力场和磁强计对地球磁场的依赖。而陀螺仪不受重力场和磁场的干扰，其直接测量机体的旋转角速率，短时间内测量结果具有较高的精度。旋转角速率经过对时间的积分可得到相应的三轴转动角度关系，其动态性能较好，但测量值随时间的变化相对较大。加速度计和磁强计易受地球重力场和磁场的干扰，均只能得到二维的角度关系，但其测量值随时间的变化相对较小，结合加速度计和磁强计可得到三维的角度关系。

可看出，若使用IMU模块融合加速度计和陀螺仪的测量结果，能有效提高姿态检测系统的测量精度。而磁强计的测量结果用于计算机体朝向方位值，进而补偿偏向误差。

图1为IMU单轴数据融合的原理图［3］。陀螺仪的测量结果对时间实时积分可得到原始角度，加速度计测量重力方向并计算机体倾斜角度。短时间内陀螺仪的测量结果较为精确，较长时间则用加速度计的测量值修正陀螺仪对时间积分所产生的漂移。最后，将未修正的测量结果与误差信号相加即可得到机体姿态角。

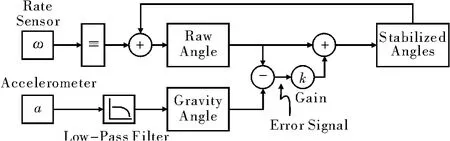
图1 IMU单轴数据融合原理

2 姿态矩阵的计算

机体姿态是描述机体的固连坐标系和参考坐标系之间角位置关系的参数。在刚体定点转动理论中，欧拉角和四元数是最常用表示姿态的两种方式。

2.1 欧拉角微分方程

动坐标系相对参考坐标系的方位可完全由动坐标系依次绕3个不同轴转动的3个转角来确定。若将机体坐标系作为动坐标系，将北东地坐标系作为参考坐标系，则偏航角Ψ、俯仰角θ、横滚角φ就是一组欧拉角，如图2所示。

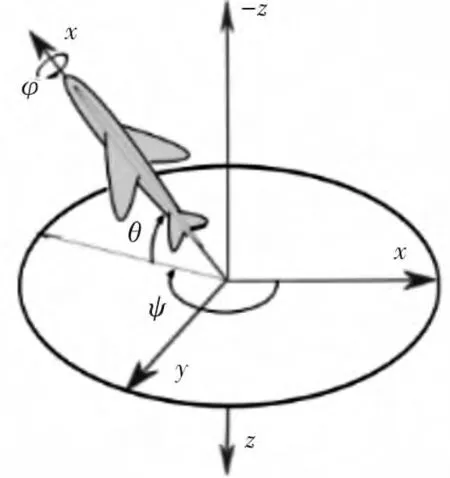
图2 欧拉角组

用ωbEb表示机体坐标系相对参考坐标系的角速度矢量在机体坐标系轴向的分量构成的列矩阵，则由图2可看出，ωbEb和 Ψ、θ、φ 的关系［4］

则有欧拉角微分方程

由欧拉角微分方程可直接得到机体的航向和姿态角，且用欧拉角法得到的姿态矩阵始终是正交矩阵，用此矩阵进行传感器信息的坐标变换时不存在非正交误差。但微分方程中三角函数的运算给实时计算带来了一定困难，当θ=90°时方程式出现“奇点”，故欧拉角微分方程不适用于全姿态工作。

2.2 四元数微分方程

四元数的数学概念是1843年由Hamilton首先提出，目的是利用复数的方法研究空间几何。四元数由1个实数单位1与3个虚数单位i、j、k组成，其形式为

在刚体定点转动理论中，动坐标系相对参考坐标系的方位等效于动坐标系绕某一个固定轴转动一个角度θ。若用u表示固定轴向的单位矢量，则动坐标系的方位可表示为［5］

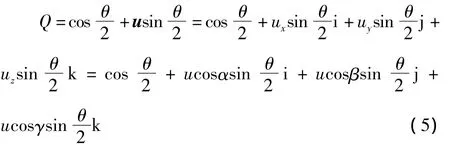
式中，cosα、cosβ、cosγ 表示旋转轴与参考坐标系轴间夹角的方向余弦值。因此，一个四元数既可表示转轴的方向，又可表示转角的大小，其标量部分表示转角一半的余弦值，其矢量部分表示瞬时转轴方向、瞬时转动轴与参考坐标系轴间夹角的方向余弦值。

根据四元数的运算性质，得到四元数微分方程

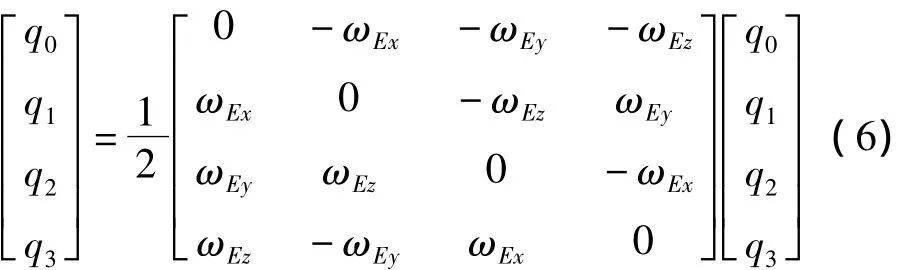
由此可看出，四元数能弥补通常描述角运动的3个欧拉角参数在运动控制系统中的不足。

3 基于四元数的姿态解算

3.1 Gauss－Newton迭代

Gauss－Newton迭代法的基本思想是使用泰勒级数展开式近似代替非线性回归模型，通过多次的迭代、修正回归系数，使回归系数不断逼近非线性回归模型的最佳回归系数，并最终使原模型的残差平方和达到最小。

Gauss－Newton迭代通常用于解决非线性最小二乘问题，目的是使原模型的残差平方和

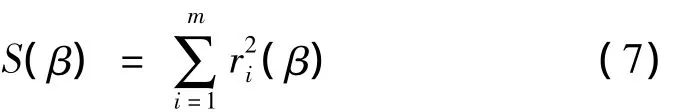
最小。迭代公式为

3.2 卡尔曼滤波器

在仿人机器人步行姿态控制中，需要对陀螺仪和加速度计所测得的数据进行综合和校正，简单的均值滤波难以满足精度和实时性的要求。卡尔曼滤波是一种最优化自回归数据处理算法，其在控制、通讯、导航等现代工程方面均有着广泛应用。文献［6］描述了一个利用GPS和磁强计来补偿姿态误差的卡尔曼滤波器，但未给出详细信息。本文根据文献［7］提出一种用于估算全姿态角的离散卡尔曼滤波数学模型，并对加速度计和陀螺仪数据进行滤波融合，进而得到更准确的角度值。

设系统状态方程为

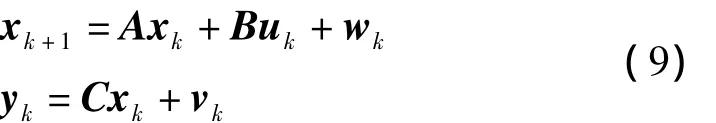
其中，X是状态矢量;A是状态转移矩阵;B是控制矩阵;u是系统输入矢量;w是协方差矩阵为Qk的过程噪声矢量;y是量测矢量;C是系统观测矩阵;v是协方差矩阵为Rk的量测噪声矢量。卡尔曼滤波器算法如下［8］:

(1)时间传播。

状态矢量的时间传播

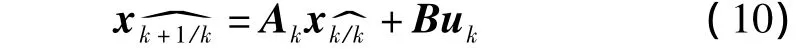
协方差矩阵的时间传播

(2)测量更新。计算卡尔曼增益矩阵

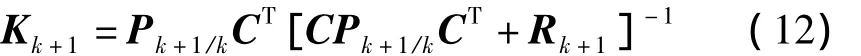
更新状态估计

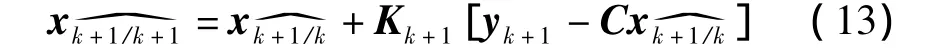
更新协方差矩阵

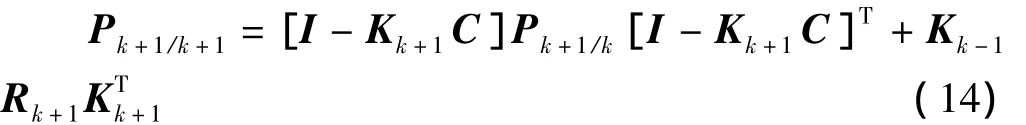
实验中，假设单位时间T内机器人匀速运动，定义状态转移矩阵［9］

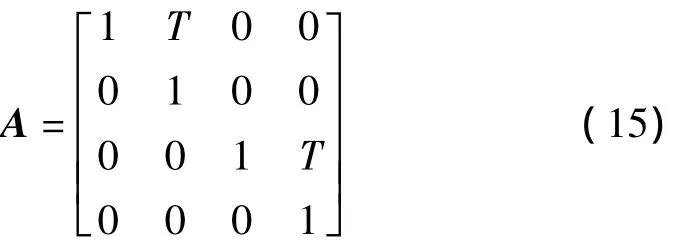
定义控制矩阵B为单位阵，由系统方程和观测状态可知观测矩阵

在动态数据采集的基础上，通过卡尔曼滤波有效地补偿了传感器漂移与测量噪声等因素对加速度计和陀螺仪的干扰，从而减小了姿态测量的误差，提高了运算精度。

3.3 姿态解算

仿人机器人运动控制系统的核心任务是机体实时姿态解算，惯性测量单元实时检测机体旋转角速度和地球重力场、磁场等信息，主控微处理器通过I2C接口以低功耗形式定时读取传感器数据，并经数据融合、卡尔曼滤波、姿态解算等算法实时计算以四元数和欧拉角形式输出的无漂移与无累积误差的三维全姿态角。全姿态解算原理如图3所示。

图3 全姿态解算原理

将加速度计和磁强计的数据进行融合，经过Gauss－Newton迭代得到姿态误差速率;陀螺仪直接通过四元数微分方程得到姿态四元数速率。姿态四元数速率加上姿态误差速率，再取对时间的积分得到姿态四元数。而四元数(w，x，y，z)到欧拉角(φ，θ，Ψ)的转换关系如下

4 实验结果

图4是参加RoboCup Soccer比赛用的仿人机器人，其运动控制系统选用基于ARM Cortex－M3内核的微控制器LPC1768作为姿态解算和步态规划的运算平台，操作频率可达100 MHz。惯性测量单元选用GY－80模块，其包括加速度计 ADXL345、磁强计HMC5883L和陀螺仪L3G4200D。两者之间通过I2C总线通信，完成主机对从机指令的写入及数据的读取。

图4 仿人机器人I－Kid

首先，编写并调试主控微处理器LPC1768和IMU之间的I2C通信。I2C通信有硬件模式和软件模式两种，前者直接调用I2C的控制函数完成数据传输，后者需要使用程序控制SCL、SDA线输出高低电平模拟I2C协议的时序。考虑到仿人机器人机体姿态解算的实时性要求，实验选用硬件I2C模式。

图5所示是LPC1768串口输出的IMU传感器信息。主机通过I2C总线读取从机寄存器数据，经过整合处理分别得到三轴向加速度矢量、三轴向角速度矢量和机体朝向方位值，并可通过串口输出显示。

图5 IMU传感器信息

在RoboCup比赛中，仿人机器人运动控制系统的一个关键任务就是准确获取机体姿态信息。将本文所述姿态解算算法移植到I－Kid机器人运动控制平台，通过主控微处理器采集传感器数据，运行卡尔曼滤波算法，计算机体姿态角。在采用滤波算法前后，机器人快速前进的输出波形如图6所示，机器人跌倒的输出波形如图7所示。

图6 采用滤波器前后机器人前进状态倾斜角度输出对比

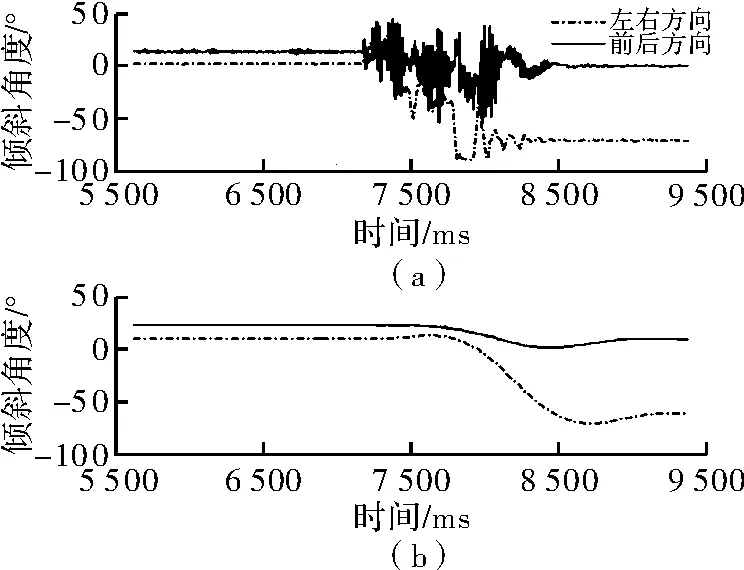
图7 采用滤波器前后机器人跌倒状态倾斜角度输出对比

由此看出，经滤波算法检测到的倾斜角度值可用于机体跌倒姿态的判定，但存在着0.5 s的时间延迟，不利于机体跌倒的立即检测。

图8是I－Kid机器人的姿态解算流程，图9是其机体姿态角的实时显示。实验结果表明，文中所述姿态解算得到的机体姿态角与仿人机器人姿态动态基本吻合。

5 结束语

本文研究了惯性测量单元的传感器性能，提出一种融合多传感信息、基于四元数的姿态解算算法。针对加速度计测量噪声和陀螺仪漂移误差，引入卡尔曼滤波器，提高了运算精度。实验结果与实际比赛情况表明，在考虑热噪声、机械噪声及惯性器件误差等因素的情况下，基于四元数的仿人机器人机体姿态解算可满足RoboCup Soccer的比赛需求，并具有较好的稳定性。