射频特征对MUSIC算法的影响分析

程亚娇，刘晨东，沈志博

(西安电子科技大学电子工程学院，陕西西安 710071)

二维波达方向(Direction of Arrival，DOA)估计是阵列信号处理的一个重要研究领域，其主要目的是通过提取空间中按一定方式排列的传感器阵列所接收信号的有用特征，来估计信号的空域方位参数，在雷达、气象、通信、声呐等相关领域中都有广泛的应用［1－3］。经典的DOA估计算法是基于接收信号相关矩阵特征分解的MUSIC算法［4］。MUSIC算法是一种空间谱估计算法，利用信号子空间和噪声子空间的正交性，构造空间谱函数，通过谱峰搜索来检测信号的DOA，可处理同频不同方向的窄带信号，并可获得高精度的方位信息，适应于现代电子战中复杂的电磁环境，所以成为测向系统中相对成熟、应用较为广泛的方法［5－7］。国内外研究学者对MUSIC算法进行了多方面研究［8－9］，大部分是基于MUSIC算法原理对其进行算法改进，在这些文献中仅研究了算法本身对测向性能的影响，没有建立起射频目标特征与测向性能的关系，而MUSIC测向性能发挥的优劣与辐射源的频率、信号持续时间以及信噪比都有密切的关系，因此，本文对测向过程中辐射源射频目标特征对测向性能的影响进行分析，并对不同射频目标影响下的MUSIC估计算法进行了仿真。

1 MUSIC算法基本原理

MUSIC算法的基本思想是将任意阵列输出数据协方差矩阵进行特征分解，从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间，然后利用这两个子空间的正交性来估计信号的参数。所以MUSIC算法首先计算样本自相关矩阵Rxx，然后对Rxx进行特征值分解，得到主特征值λ1，…，λp和次特征值λp+1，…，λM，其中M为阵元数，主特征值对应的是信号子空间S，次特征值对应的是噪声子空间G，利用式(1)

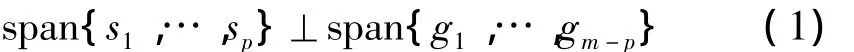
可以得出谱估计表达式

或

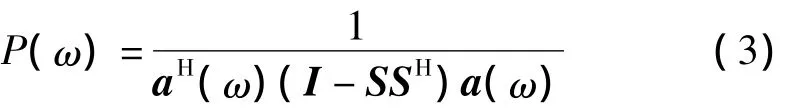
式(2)是基于噪声子空间，式(3)是基于信号子空间，其中a(ω)为阵元对ω方向上的信号源信号的影响，可称为阵列向量，上标H表示复共轭转置。

选取阵列模型为均匀线阵，阵元数M=10，阵元间距 d=λ/2，测角范围为 －90°～90°，快拍数 L=512。空间中有3个信号源，到达方向分别为 －5°，30°和60°，图1显示了单次估计的特征值分布，并对其进行了归一化处理，所以最大值为1。可以看出有3个较大的特征值，代表了当前3个信号源，其余为噪声。由于估计时选用的信号信噪比较高，且3个信号之间相互独立，信号子空间和噪声子空间正交性较好，所以3个主特征值比较明显，而其余的很小，接近于0。图2是MUSIC算法的估计结果，说明该算法能较好地估计出到达方向。

图1 MUSIC算法特征值分布

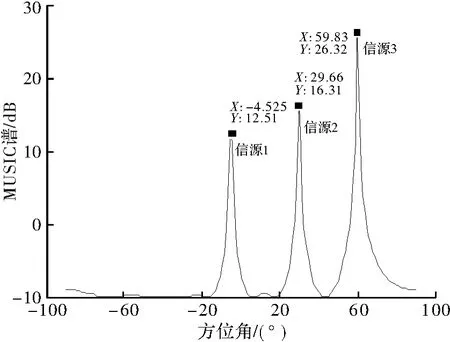
图2 MUSIC算法估计结果

2 射频目标特征对MUSIC算法的分析

2.1 频率对MUSIC算法的影响

射频目标频率变化对DOA估计性能产生影响。频率变化对应着波长λ的改变，若波长变化的范围始终满足d≤λ/2，则只会影响DOA估计误差，若频率变化范围过大，使d＞λ/2，则不仅会影响DOA估计误差，还会在空间谱上出现虚假谱峰的定量关系。

对DOA估计的方向角θ位于区间［－π/2，π/2］，设θ为真实的波达方向角，θ^为估计值，λ'为谱峰搜索时的频率，λ0为频率变化均值对应的波长，则有

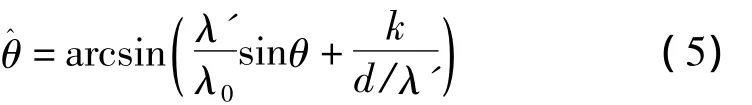
(1)当阵元间距不大于载波的半波长。此时d/k≤1/2，λ'/λ0≤1，为满足条件，k 只能取 0，式(5)可改写为

这种情况下可以估计出唯一的波达方向，没有虚假谱峰。DOA的估计精度与的比值有关，谱峰搜索频率与快拍期间内频率均值偏差越大，则DOA估计精度也就越差。

(2)当阵元间距大于载波的半波长。此时可分为两种情况进行讨论，为简单起见，假设 λ'/λ0≈1，则式(5)简化为

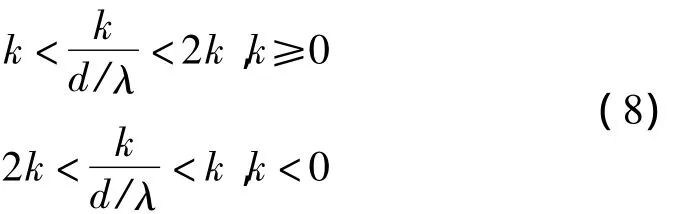
当d/λ≥1时，满足

k可取0值以及±1，这种情况下一定会出现虚假谱峰，且d/λ越大，虚假谱峰越多。对于每一个信源而言，令=n+Δ，n为整数部分，Δ为小数部分。若Δ=0，则只有整数部分，那么将有n个谱峰，其中n－1个虚假谱峰;若Δ≠0，则式(5)改写为

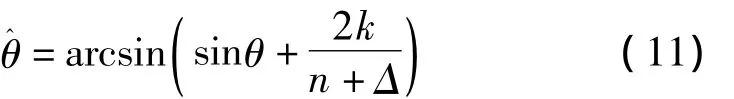
2.2 信号持续时间对MUSIC算法的影响

信号持续时间对应着快拍数L，信号持续时间越长，L越大，一般要求快拍数L大于阵元数M，若每次快拍的持续时间为τL，则要求信号的持续时间τ满足

否则数据协方差矩阵会出现病态，造成矩阵损失秩，进而影响估计性能。

2.3 信噪比对MUSIC算法的影响

对于等距均匀线阵，当快拍数L及阵元数M足够大时，角度估计的克拉美罗界CCRB为

其中，SNRi(i=1，…，M)是指第 i个信号的信噪比。角度分辨力决定了两个相近信源能否分辨，由于MUSIC算法要进行谱峰搜索，信号空间的峰值对应着信号的角度。对于两个角度相近信源θ1和θ2，P(θ1)为 θ1的谱估计函数，P(θ2)为 θ2的谱估计函数，则峰值谱估计函数Ppeak为

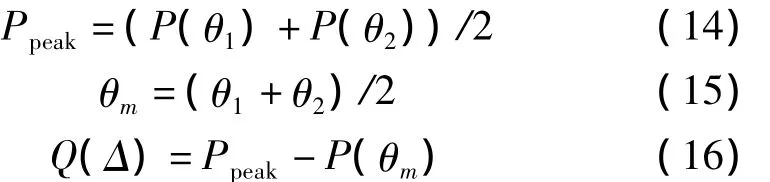
式中，θm为θ1和θ2的平均角度;Q(Δ)为谱分辨能力，当Q(Δ)＞0时，Q(Δ)是可分辨的，且分辨力为 Δ。MUSIC算法的信号谱分辨能力与分辨力Δ近似满足

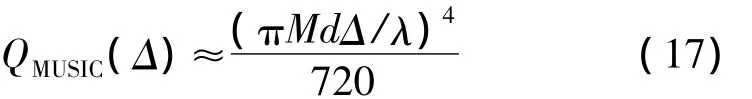
信噪比门限满足

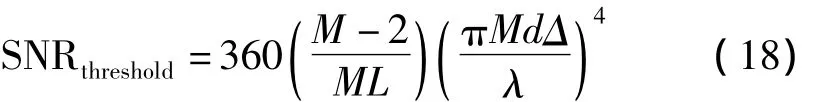
由式(17)可知，用MUSIC算法估计不相干信源所需的最低信噪比是有限制的，结合式(18)可以看出，πMDΔ/λ越小，MUSIC要分辨两个信号所需要的信噪比越高，信号的谱分辨能力越低，这说明MUSIC算法并不适用于信噪比过低的情况。

3 仿真结果分析

仿真条件1 仿真选取了DOA分别为－5°，30°和60°的3个信源，快拍数L=1 024，假设频率在快拍时间内均匀变化，图3和图4给出了频率变化对MUSIC估计性能的影响。

从图3可以看出，在频率恒定情况下仅有3个特征值，频率变大和频率变小时特征值的个数增加，但从图4来看，此时的频率变化只影响了DOA估计误差，并未出现虚假谱峰。这是因为频率导致的波长变化的范围始终满足d≤λ/2，没有出现d＞λ/2。

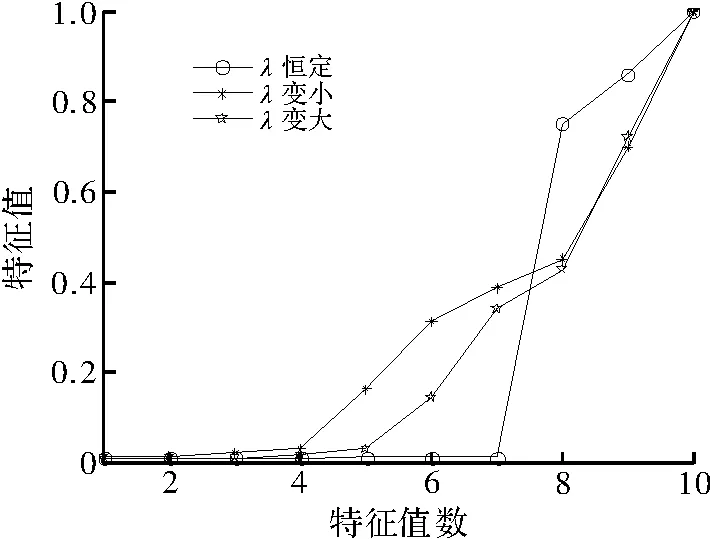
图3 MUSIC算法特征值分布影响

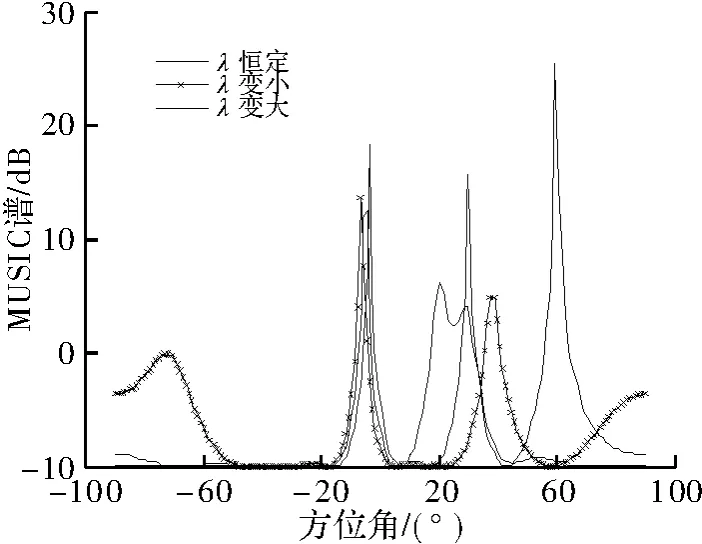
图4 MUSIC算法影响

仿真条件2 现选取阵元数M=8，3个信源到达方向分别为－15°，30°和40°，图5给出了在不同快拍数下的估计结果，图6则说明了快拍数对MUSIC算法测向误差的影响。

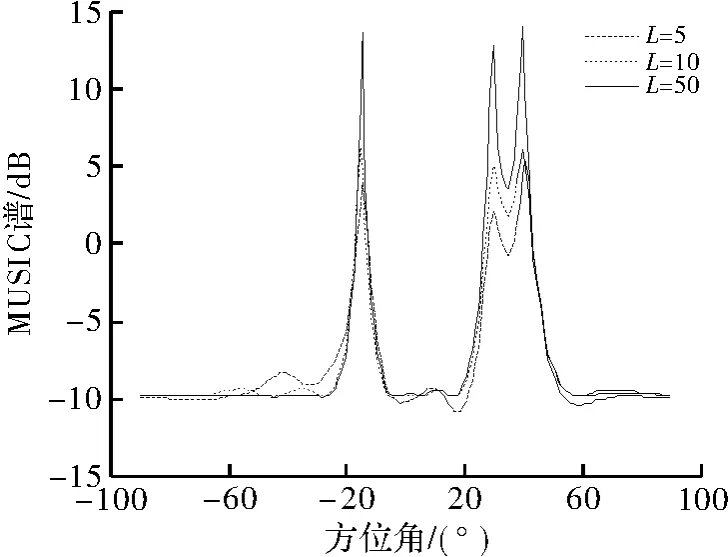
图5 不同快拍数下的测向结果

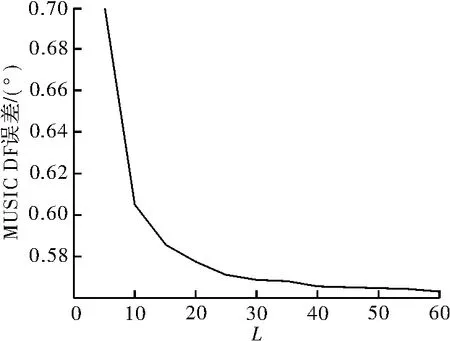
图6 快拍数对测向误差的影响

比较图5中不同快拍数下MUSIC算法估计结果，发现随着快拍数的增加，估计的结果越来越精确，快拍数为5时刚能分辨出相近的角度，但峰值并不集中。增至10时，峰值增加且更加集中;增至50时，就能清晰地分辨出这3个信号源各自的角度值。结合图6的误差曲线，发现随着快拍数增加，MUSIC测向误差逐渐减小，这与理论分析保持一致。

仿真条件3 选取阵元数M=8，3个信源到达方向分别为 －15°，30°，40°，快拍数为 50，图 8 为不同信噪比下的估计结果。

图7 不同SNR下的测向结果

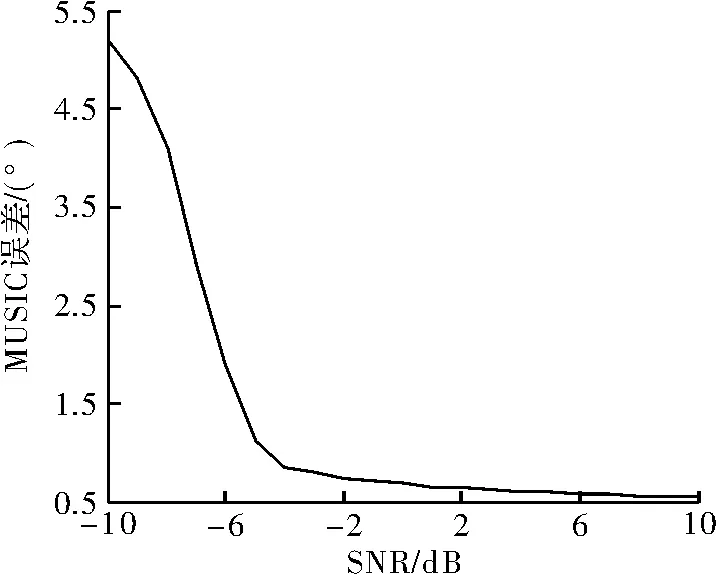
图8 SNR对测向误差的影响

由图7可以看出，随着信噪比的增加，MUSIC算法的估计结果更精确。在信噪比为－5 dB时谱峰较低且不集中，待增至0 dB时精度已有所提高，当信噪比增至5 dB时角度分辨率进一步提高，峰值较高并且集中，能清晰分辨出相近的角度。图7的误差曲线也说明了随着SNR增加，MUSIC测向误差逐渐减小，仿真结果与理论分析吻合。

4 结束语

采用MUSIC法测向时，辐射源射频特征对其测向结果是有影响的。频率影响波长，影响阵元间距与载波半波长的关系，进而影响测向结果的估计精度，甚至会产生虚假谱峰;信号持续时间影响快拍数，在一定范围内，快拍数的增加会提高测向估计精度;用MUSIC算法估计不相干信源所需要的最低信噪比是有限制的，在合理范围内信噪比的增加同样会提高测向性能。通过分析射频特征对MUSIC算法的影响，能在选择算法时更加清楚算法的适用性，从而获得更好的谱分辨率。

［1］司伟健，蓝晓宇，刘学.提高二维DOA估计分辨率的改进MUSIC算法［J］.西安电子科技大学学报:自然科学版，2012，39(2):138 －144.

［2］韩芳明，张守宏，潘复平.阵列误差对MUSIC算法性能的影响与校正［J］.西安电子科技大学学报:自然科学版，2003，30(5):585 －589.

［3］路鸣，保峥.改善MUSIC空间谱估计分辨率的后处理算法［J］.电子学报，1990，18(4):14 －17.

［4］Schmidt R O.Multiple emitter location and signal parameter estimation［J］.IEEE Transactions on AP，1986，34(2):276 －280.

［5］高星辉.修正MUSIC算法对信号DOA的估计［D］.广州:华南师范大学，2002.

［6］王月瑜.基于MUSIC算法的二维DOA估计［D］.哈尔滨:哈尔滨工程大学，2005.

［7］韩卫杰.改进MUSIC算法在DOA估计中的研究［D］.成都:西南交通大学，2006.

［8］唐马可.基于MUSIC算法的空间谱估计技术的研究［D］.重庆:重庆大学，2008.

［9］高星辉，张承云，常鸿森.改进MUSIC算法对信号DOA的估计［J］.系统仿真学报，2005(6):223－225.