黏弹性EDA介质中地震波的衰减特性研究
2015-12-17何现启朱自强彭凌星戴光明
何现启 朱自强 彭凌星 戴光明
1)中国长沙410008湖南省交通规划勘察设计院
2)中国长沙410083中南大学地球科学与信息物理工程学院
引言
在隧道施工和矿山开采过程中,我们可以由地震波的速度及其衰减分析推断地下冷热水的运移和储存情况,从而进行地下水资源的评价和地下工程突水、涌泥等地质灾害预报.地震波振幅的衰减随岩石物理性质的变化较地震波速度随岩石物理性质的变化更为灵敏,故推测振幅衰减可能携带了比速度更多的岩石物理性质方面的信息.此外,振幅衰减还与岩石的应力状态密切相关(Best et al,1994;Shatilo et al,1998;梁锴,2009).
国外研究人员对黏弹性各向异性介质中地震波的传播特征及VTI(transverse isotropy media with vertical symmetry axis)介质中地震波的衰减特征进行了深入研究.Samec和Blangy(1992)及Blangy(1994)对各向异性介质中地震波的黏弹性、衰减、吸收、AVO等现象进行了探讨;Carcione(1995,2001)以及Carcione和Cavallini(1997)研究了黏弹各向异性介质的本构方程(即应力-应变关系),发展并完善了黏弹各向异性介质的基本理论;ˇCerveny和Pšenˇcík(2005a,b)深入研究了黏弹性单斜各向异性介质中SH 波相速度、偏振方向等随非均匀角变化的规律;Zhu和Tsvankin(2006,2007)分析了黏弹VTI介质和正交各向异介质中平面波相衰减和群衰减的特征,并推导了弱各向异性近似表达式;Vavryˇcuk(2007)给出了黏弹性VTI介质中非均匀波的群衰减系数随群角的变化规律;Vavryˇcuk(2008)利用摄动法推导了黏弹性VTI介质中地震波的速度、衰减系数和品质因子的表达式;Behura(2006)研究了VTI介质和正交各向异性介质中相衰减系数和群衰减系数的变化规律,并利用谱比法进行衰减估计;Vavryˇcuk(2009)采用高阶摄动法推导了弱各向异性衰减参数即品质因子的表达式.
国内许多研究人员也对黏弹性各向异性介质中地震波的衰减特性及其应用前景进行了深入探讨.张中杰等(1999)通过考察介质中的应力-应变关系,建立了非弹性EDA介质中具有非弹性效应的地震波动方程组;杨顶辉等(2000)通过固体与液体的相互作用探讨了双相各向异性研究存在的问题与应用前景;郝奇等(2010)利用改进的摄动理论对弱各向异性黏弹性介质中的非均匀平面波的传播特征进行深入探讨,并给出了误差分析,得到一些有益的结论;郭智奇等(2010)研究了各向异性介质的衰减特性;聂建新等(2010)对黏弹性各向异性介质中的波频散与衰减特性进行了研究;韩颜颜(2011)采用数值模拟法对双相黏弹EDA介质中地震波的波场特征进行了详细分析.
上述研究主要是针对极端各向异性和VTI各向异性介质中地震波衰减及衰减估计问题,对 HTI和 EDA 介质的研究则较少.本文拟利用特殊分量法(ˇCerveny,Pšenˇcík,2005a,b;何现启,2010;何现启等,2014),由Christoffel方程推导出黏弹性HTI和EDA介质中均匀、非均匀P波、SV波和SH波的精确相速度,旨在研究SH波相速度随非均匀角变化的规律;然后从Christoffel方程出发推导出HTI和EDA介质中均匀、非均匀地震波的精确相衰减系数和群衰减系数.
1 黏弹性EDA介质中均匀地震波的衰减特性
波数k除了由Christoffel方程直接求解外,还可由慢度和相速度间接得到,具体表达式为(ˇCerveny,Pšenˇcík,2005a,b;Taner,Koehler,1969;Tsvankin,1997)

式中,k为波数,v为相速度,ω为角频率,σ为复数,n和m为相互垂直的实单位向量,D为不均匀参数,是实数标量.下面主要利用相速度v与波数k的关系来求解波数k和衰减系数.
1.1 黏弹性EDA介质中均匀地震波的相速度
黏弹性各向异性介质中地震波的相速度可由Christoffel特征方程求解,且只有行列式为零才有非零解,即
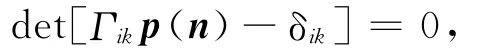
其中,Γikp(n)=aijklpjpl.式中,p为地震波的慢度;δij为克罗内克符号;aijkl=cijkl/ρ为密度归一化的复黏弹性系数,其取值与频率有关;ρ为密度.
将均匀波的慢度向量p=σn代入上式,可导出黏弹性EDA介质中复参数的表达式为(梁锴,2009;何现启,2010)

其中,

式中:cij为介质的弹性系数矩阵元素;θ和φ分别为波传播方向的极角和方位角;φ0是EDA介质对称轴相对HTI介质对称轴的转角,称为对称轴方位角.
由v=1/|ReσP|(ˇCerveny,Pšenˇcík,2005a,b),可得复相速度为对上述结果进行退化验证得到的相速度表达式与HTI介质中的相速度表达式相同.

1.2 黏弹性EDA介质中均匀地震波的衰减系数
由式(1)和(5)可得波数为
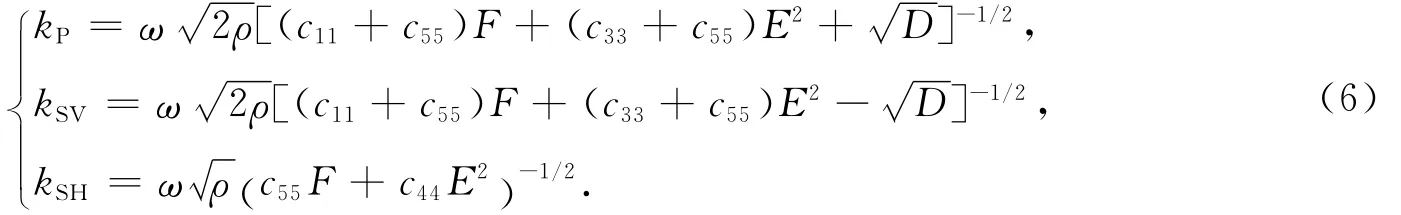
1.2.1 SH波相衰减系数
式(6)中SH波的波数写成复数形式为


由相衰减系数的定义A=kI/kR(Zhu,Tsvankin,2006,2007)可得SH波相衰减系数ASH为

在xoy平面内,将θ=0代入式(4),可得E=sin(φ-φ0),F=cos2(φ-φ0),将其代入式(7),则有

据相衰减系数定义有
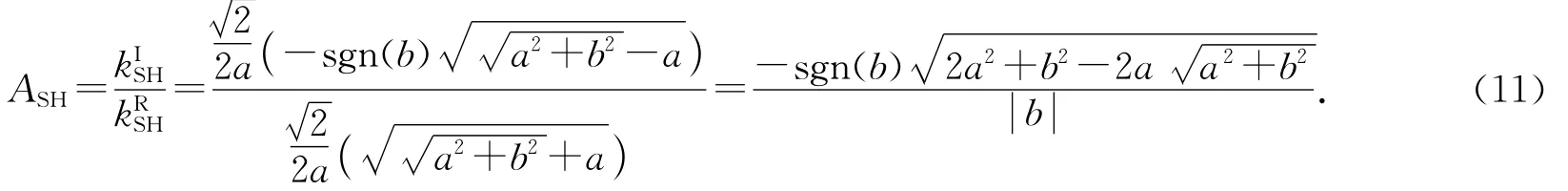
对于均匀波,非均匀系数ξ=0(波数的实分量与虚分量的夹角),均匀SH波群衰减系数(Ag=kIg/kgR)与相衰减系数相等(ˇCerveny,Pšenˇcík,2005a,b;Zhu,Tsvankin,2006,2007).
1.2.2 P波和SV波衰减系数
由式(4),将复弹性系数的实部与虚部分开可得
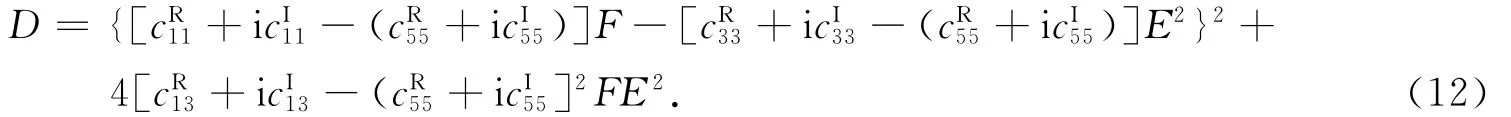
令D=c+i d,即将D的实部与虚部分开,由上式可得其实部c与虚部d分别为
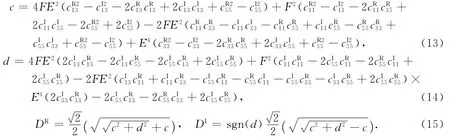
由式(6),并令kP=x+i y,将kP分解成实部与虚部可得

同理可得

其中,
极端各向异性介质是指介质中任一点处沿任意方向的弹性性质均不同,其具有21个独立弹性参数,其群衰减系数Ag=(kI/kR)cosξ(1+tanξtanψcosφ)(ξ为非均匀角,ψ为群角,φ为方位角)(何现启,2010),故可知均匀P波和SV波的群衰减系数与相衰减系数相等.
2 黏弹性EDA介质中非均匀地震波的衰减特性
2.1 SH波的相速度和慢度
将非均匀波的慢度向量p=σn+i Dm(m为实单位向量,垂直于n),代入det[Γikp(n)-δik]=0,可求出黏弹性EDA介质中复参数的表达式为(ˇCerveny,Pšenˇcík,2005a,b;何现启,2010)
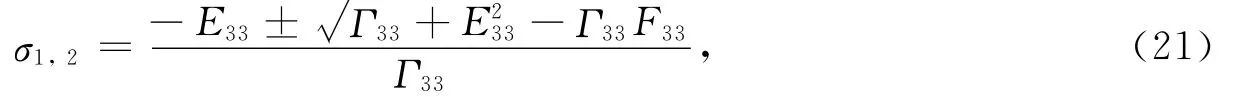
其中,
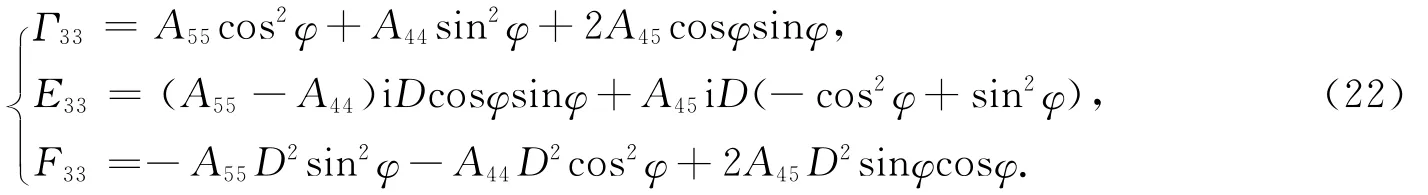
由式(21),可得SH波的相速度为

SH波的慢度为
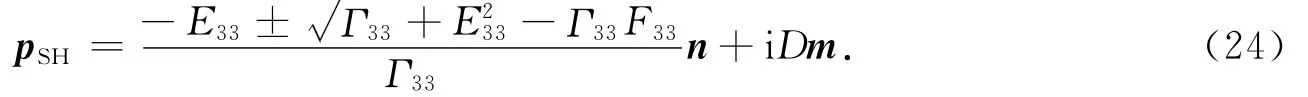
2.2 SH波的相衰减系数
由式(2)和式(23)可得SH波的波数为

令Γ33=a+i b,代入式(22),并将实部与虚部分开可得

令E33=c+i d,代入式(22),并将实部与虚部分开可得

令F33=x+i y,代入式(22),并将实部与虚部分开可得

令

将式(30)代入式(29)可得
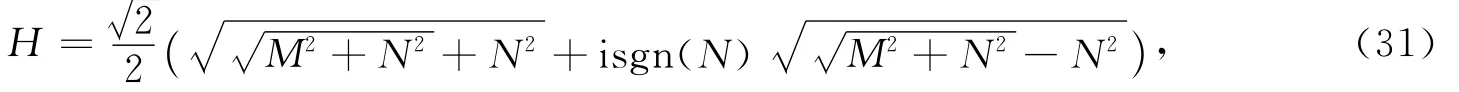
SH波的波数为

SH波的衰减系数为
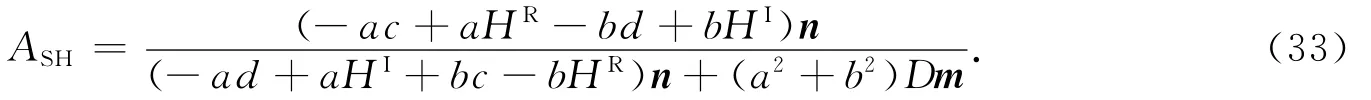
2.3 SH波的群衰减系数
由极端各向异性介质中群衰减系数 Ag=(kI/kR)cosξ(1+tanξtanψcosφ)(ξ为非均匀角,ψ为群角,φ为方位角)(Zhu,Tsvankin,2006,2007)和式(33)可得
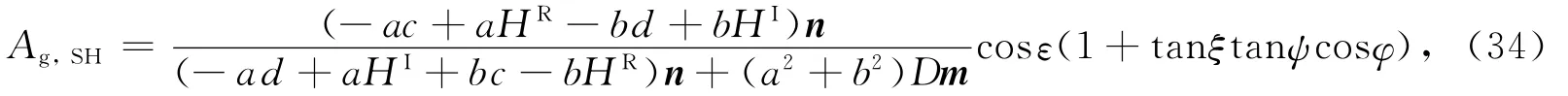
此即为SH波的群衰减系数.
3 数值计算
本节主要通过数值计算研究EDA介质中均匀、非均匀SH波的相衰减和群衰减特性.首先给出HTI介质的弹性系数矩阵,然后根据弹性EDA介质弹性系数矩阵与HTI介质弹性系数的关系,通过旋转对称轴得到EDA介质的弹性系数矩阵,再将其代入相应的计算公式即可得到EDA介质中地震波的衰减系数.
3.1 EDA介质中SH波的相衰减系数
黏弹性 HTI介质的弹性系数矩阵为(ˇCerveny,Pšenˇcík,2005b)

将该弹性系数矩阵通过欧拉变换逆时针旋转60°,则可得到黏弹性EDA介质的弹性系数矩阵,以此矩阵表示的介质模型标记为模型1,即通过旋转HTI对称轴得到的具有水平对称轴的EDA介质.将上述矩阵代入式(11)可计算均匀SH波的相衰减系数,并用Matlab成图,结果显示于图1.可以看出:相速度随方位角的变化近似成椭圆,椭圆的长轴指示裂隙的方位,短轴指示EDA介质对称轴的方位;相衰减系数随方位角的变化呈以裂隙方位角为对称轴的对称花瓣状,沿介质对称轴方向(即垂直裂隙方向)衰减系数较大,平行裂隙方向衰减系数较小.这些均表明,均匀SH波的相速度和相衰减系数均可指示裂隙的走向,且相衰减系数相对于方位角的变化更敏感,更能反映地下介质的精细构造.

图1 EDA介质中均匀SH相速度(a)和相衰减系数(b)与方位角的关系(模型1)极坐标角度表示方位角,虚线圆圈表示相速度(单位为km/s)(a)和相衰减系数(b)的大小Fig.1 Relationship between phase velocity(a)and phase attenuation coefficients(b)and azimuth angle for homogeneous and inhomogeneous SH wave in EDA media(model 1)The polar coordinate represents azimuth angle.Dashed circle indicates the phase velocity(km/s)(a)and the phase attenuation coefficient(b)
为研究相衰减系数随非均匀角的变化情况,下面通过模型2的数值计算来研究分析.模型2(EDA)也是具有水平对称轴的各向异性介质,与模型1不同的是模型2由EDA弹性系数矩阵直接表示,而不是由HTI弹性系数矩阵表示,该模型的主要特性以弹性为主.模型2(EDA)的弹性系数矩阵为

将上式代入式(33)计算得到非均匀SH波相衰减系数,用Matlab成图,结果如图2所示.可以看出,在对称轴方向(垂直裂隙方向),非均匀SH波相衰减系数随非均匀角的增大而增大,且其对称轴与介质对称轴的夹角也相应增加.因此,利用相衰减与相角的相互关系来反演裂隙的走向时首先还要明确地震波的非均匀角大小,对于非均匀角较小的情况可将相衰减的对称轴方向近似为裂隙的走向,这是均匀波与非均匀波的不同之处.上述对应关系可通过退化成 HTI介质来验证,退化结果与 ˇCerveny和Pšenˇcík(2005a,b)及Tsvankin(1997)相同.

图2 EDA介质中非均匀SH波相衰减随非均匀角ξ(a)和相角θ(b)的变化关系(模型2).参数同图1Fig.2 The characteristics of phase attenuation for inhomogeneous SH wave varying with inhomogeneous angleξ(a)and phase angleθ(b)(model 2)where the illustrations are the same as Fig.1
3.2 EDA介质中非均匀波的群衰减系数

图3 非均匀SH波群衰减系数随非均匀角ξ(a)和群角ψ(b)的变化关系Fig.3 Relation of SH inhomogeneous wave varying with the inhomogeneous angleξ(a)and group angleψ(b)
非均匀SH波群衰减系数由式(34)计算而得,用Matlab成图,结果如图3所示.可以看出,群衰减系数相对于非均匀角的变化规律与相衰减系数相似,即在对称轴方向(垂直裂隙方向)非均匀SH波的群衰减系数随非均匀角的增大而增大,且其对称轴与介质对称轴的夹角也相应增加.图3b给出了非均匀角为60°时,非均匀SH波群衰减系数与群角的变化关系.可见,群角只影响群衰减系数的大小,对其对称关系并无任何影响,且随群角的增大群衰减系数也相应增大.
4 讨论与结论
本文基于前人的研究成果,从Christoffel方程出发,推导出非均匀、均匀黏弹性EDA介质中地震波的三维相速度、相衰减系数、群衰减系数的计算公式,并将推导结果进行退化验证,结果表明其与HTI介质中的计算结果较吻合.利用Matlab进行数值计算,研究了相速度、相衰减系数、群衰减系数与裂隙方向的关系.依据数值计算结果,本文结论如下:
1)在均匀介质中SH波的相速度和相衰减系数均可指示裂隙的走向,且相衰减系数对方位角的变化更敏感,更能反映地下介质的精细构造.
2)非均匀介质中SH波相衰减系数随非均匀角的增大而增大,且其对称轴与介质对称轴的夹角也相应增加.在利用相衰减与相角的相互关系来反演裂隙走向时,首先要明确地震波非均匀角的大小.在非均匀角较小的情况下,将相衰减的对称轴方向近似为裂隙的走向.群衰减系数随非均匀角的变化规律与相衰减系数相似,群角只影响群衰减系数的大小,对其对称关系并无任何影响,且随着群角的增大,群衰减系数也相应增加.
3)地震波振幅的衰减随岩石物理性质的变化比地震波速度随岩石物理性质的变化更为灵敏,因此衰减特性比速度特性携带了更多的岩石物理性质信息.
郭智奇,刘财,冯晅,韩颜颜,王晓欢.2010.各向异性衰减与AVO分析[J].吉林大学学报:地球科学版,40(2):432-438.
Guo Z Q,Liu C,Feng X,Han Y Y,Wang X H.2010.Attenuation anisotropy and AVO analysis[J].Journal of Jilin University:Earth Science Edition,40(2):432-438(in Chinese).
韩颜颜.2011.双相粘弹EDA介质地震波场数值模拟与特征分析[D].长春:吉林大学:2-6.
Han Y Y.2011.Seismic Wave Field Modeling and Character Analysis of Two-Phase Viscoelastic EDA Media[D].Changchun:Jilin University:2-6(in Chinese).
郝奇,何樵登,王德利.2010.利用改进的摄动理论研究各向异性弱粘弹性介质中的非均匀平面波[J].吉林大学学报:地球科学版,40(1):195-202.
Hao Q,He Q D,Wang D L.2010.Inhomogeneous plane wave in anisotropic weakly viscoelastic media by improved perturbation theory[J].Journal of Jilin University:Earth Science Edition,40(1):195-202(in Chinese).
何现启.2010.EDA介质中地震波的传播特征及参数反演研究[D].长沙:中南大学:99-133.
He X Q.2010.The Study of Seismic Wave Propagation in EDA Medium and Parameters Inversion[D].Changsha:Central South University:99-133(in Chinese).
何现启,朱自强,鲁光银.2014.EDA介质中地震波的传播特征[J].地震学报,36(3):403-416.
He X Q,Zhu Z Q,Lu G Y.2014.The exact propagation characteristics of seismic wave in EDA media[J].Acta Seismologica Sinica,36(3):403-416(in Chinese).
梁锴.2009.TI介质中地震波的传播特征与正演方法研究[D].青岛:中国石油大学:20-31.
Liang K.2009.The Study on Propagation Feature and Forward Modeling of Seismic Wave in TI Media[D].Qingdao:China University of Petroleum:20-31(in Chinese).
聂建新,杨顶辉,巴晶.2010.含泥质低孔渗各向异性黏弹性介质中的波频散和衰减研究[J].地球物理学报,53(2):385-392.
Nie J X,Yang D H,Ba J.2010.Velocity dispersion and attenuation of waves in low-porosity-permeability anisotropic viscoelastic media with clay[J].Chinese Journal of Geophysics,53(2):385-392(in Chinese).
杨顶辉,张中杰,滕吉文,王光杰.2000.双相各向异性研究、问题与应用前景[J].地球物理学进展,15(2):7-21.
Yang D H,Zhang Z J,Teng J W,Wang G J.2000.The study of two-phase anisotropy,questions and applied prospects[J].Progress in Geophysics,15(2):7-21(in Chinese).
张中杰,滕吉文,贺振华.1999.EDA介质中地震波速度、衰减与品质因子方位异性研究[J].中国科学:E辑,29(6):569-574.
Zhang Z J,Teng J W,He Z H.2000.Azimuthal anisotropy of seismic velocity,attenuation and Qvalue in viscous EDA media[J].Science in China:Series E,43(1):17-22.
Best A I,McCann C,Southcott J.1994.The relationships between the velocities,attenuations and petrophysical properties of reservoir sedimentary rocks[J].Geophys Prosp,42(2):151-178.
Behura J.2006.Estimation and Analysis of Attenuation Anisotropy[D].Colorado:Colorado School of Mines:51-55.Blangy J P.1994.AVO in transversely isotropic media:An overview[J].Geophysics,59(5):775-781.
Carcione J M.1995.Constitutive model and wave equations for linear,viscoelastic,anisotropic media[J].Geophysics,60(2):537-548.
Carcione J M,Cavallini F.1997.Forbidden directions for TM waves in anisotropic conducting media[J].IEEE Trans Antennas Propag,45(1):133-139.
Carcione J M.2001.Wave Fields in Real Media:Wave Propagation in Anisotropic,Anelastic and Porous Media[M].Amsterdam:Pergamon:16-25.
ˇCerveny V,Pšenˇcík I.2005a.Plane waves in viscoelastic anisotropic media:Ⅰ.Theory[J].Geophys J Int,161(1):197-212.
ˇCerveny V,Pšenˇcík I.2005b.Plane waves in viscoelastic anisotropic media:Ⅱ.Numerical examples[J].Geophys J Int,161(1):213-229.
Samec P,Blangy J P.1992.Viscoelastic attenuation,anisotropy,and AVO[J].Geophysics,57(3):441-450.
Shatilo A P,Sondergeld C,Rai C.1998.Ultrasonic attenuation in Glenn Pool rocks,northeastern Oklahoma[J].Geophysics,63(2):465-478.
Taner M T,Koehler F.1969.Velocity spectra-digitalcomputer derivation and applications of velocity functions[J].Geophysics,34(6):859-881.
Tsvankin I.1997.Anisotropic parameters and P-wave velocity for orthorhombic media[J].Geophysics,62(4):1292-1309.
Vavryˇcuk V.2007.Ray velocity and ray attenuation inhomogeneous anisotropic viscoelastic media[J].Geophysics,72(6):D119-D127.
Vavryˇcuk V.2008.Velocity,attenuation,and quality factor in anisotropic viscoelastic media:A perturbation approach[J].Geophysics,73(5):D63-D73.
Vavryˇcuk V.2009.Weak anisotropy-attenuation parameters[J].Geophysics,74(5):WB203-WB213.
Zhu Y P,Tsvankin I.2006.Plane-wave propagation in attenuative transversely isotropic media[J].Geophysics,71(2):T17-T30.
Zhu Y P,Tsvankin I.2007.Plane-wave attenuation anisotropy in orthorhombic media[J].Geophysics,72(1):D9-D19.
