优化数学作业设计 落实课程标准理念

◆福建省福州市第十六中学 陈 葳

优化数学作业设计 落实课程标准理念

◆福建省福州市第十六中学 陈 葳

在数学教学中，课后作业是不可或缺的组成部分，教师在备课时，应在课标的指导下，在理解教材的基础上对作业进行优化设计，使之适应学生的学力。在教育教学中，教师应对作业进行分层，实现目标优化；通过变式，实现内容优化；设置拓展性问题，培养创造性思维；优化作业设计，实现合理的学习评价，由此，提高教学效率，减轻学生的负担。

数学作业；分层；变式；四基；课标；效率

在数学教学中,课后作业是不可或缺的组成部分,在课程改革的过程中,有人提出不留课外作业,这在初中数学教学中是不切实际的。在教学中提倡“自主、探究、合作”的方向,对培养学生的创造力是十分正确的。然而,适当的训练、严谨的思维以及四基的夯实,在一线教学中被证明是必不可少的,就如建筑高楼,创新的思维犹如美观实用的设计,四基犹如房屋的地基、墙体,缺一不可。强调夯实基础,并不等于扼杀“创造力”,相反,在坚实的基础上发展起来的创造力才是切合实际的,才能够取得成功。认知心理学认为,人的专长是由自动化技能、概念性理解和策略性知识组成。

一、在“做”中学数学，培养基本技能

1.记忆通向理解。在教学中,我们发现,如果对一些基本概念、定理不要求记忆,学生的遗忘率是很高的,就更谈不上运用了。因此,在理解的基础上记忆,在操练的过程中加深理解是很有必要的。

2.速度赢得效率。只有把基本的运算和基础的思考化为“直觉”且能够不假思索地反映出来,才能保证学生将注意力集中在“问题解决”的高级思维上,才能有时间进行更高级的数学思维活动。在教学实践中,熟练掌握基本知识、基本技能的学生,往往更能够提出更多解决问题的方法；而对基本知识、基本技能掌握不熟练的学生,则往往无法提出解决问题的方法。

3.严谨形成理性。中国的文化传统讲究“严谨治学”,而初中学生的日常经验十分有限,因此,在数学学习中,教师应注重对学生理性思维能力的培养。

4.重复依靠变式。一定的重复是必要的,只有在变化中进行重复,才能在重复中获取变化。因此,在教学中,教师应抓住思维训练这条主线,通过多种方式的变式练习,恰当地变更问题情境或改变思维角度,培养学生的应变能力,引导学生从不同途径寻求解决问题的方法,从而加深其对知识的理解。

值得注意的是,课程标准和教材是面向全国的学生,对某一所学校的学生而言,不一定具有针对性。因此,教师在备课时,应在课标的指导下,在教材的基础上对作业进行优化设计,使之适应所教学生的学力。

二、对作业进行分层，实现目标优化

《全日制义务教育数学课程标准》中明确指出：“在数学教学过程中,我们应当最大限度地满足每一位学生的数学需要,最大限度地开启每一位学生的智慧潜能……”在每个班级中,学生的学习程度和能力都是有差别的,因此,为了真正体现“面向全体”“因材施教”,对作业进行分层就很有必要。作业“分层设计”是指优化作业结构,使每个学生都能选择适合自己的作业来巩固所学。实践证明,只有针对不同层次的学生掌握知识的深度、广度要求不同,并进行弹性调节,才有利于各层次学生通过作业练习,在自己的“最近发展区”得到充分发展。

在实际教学中,针对我校 (此处指福建省福州市第十六中学,下文同)初中按照教育行政部门规定实行划片招生,学生层次跨度大；学生年龄在12～16岁之间,普遍玩心较重的特点,笔者将作业分成了三个层次,利用游戏晋级模式激发学生热情：“入门级”——夯实基础——帮助学困生；“骑士级”——巩固提高——推动中等生；“将军级”——能力拓展——培养学优生。然后,笔者引导学生自主定位,由此达到激发其潜能和作业热情的目的。实践证明,作业分层后,减轻了学生的作业负担,原来作业完成较慢的学困生作业量减少了,难度降低了,完成作业的情况也大大改善了。最根本的变化是体现了以学生主体性发展为中心的变化,从教师布置作业要学生做,转变为学生可以根据自身情况有一定的自主性选择完成。学生有更积极主动的心态对待作业,符合课程标准“重视学生在学习活动中的主体地位”这一要求。

三、通过变式，实现内容优化

在传统教学中,“题海战术”的机械重复一直以来都为众多数学教育家所诟病,但一个基本知识或基本技能的形成,需要有一定量的重复,这也是熟能生巧的道理。这种重复,不是机械、无层次的重复,而应该经过变式,由浅入深地进行排列。调查发现,标准形式有利于学生对概念的准确把握,在此基础上,教师再利用非标准式,通过变换概念的非本质属性,突出概念的本质属性,提高学生思维的灵活性,然后再利用非概念变式,有效明确概念的外延,划清概念与其周边概念之间的界限,从而加深学生对概念的理解。

例如：在“三角形的高,中线,角平分线”的作业中,就可以这样设计：

1.如图1,画出三角形ABC中BC边上的高AD及AC边上的高。 (一条高是标准图形,一条是非标准图形)

2.如图2,在三角形ABC中,∠C=90°,CD⊥AB于D,则BC边上的高为____,AB边上的高为____,BC为____边上的高。 (非标准式)

图1

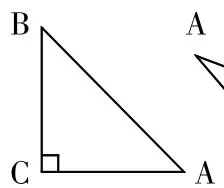
图2

图3

3.如图3,画出三角形ABC三边上的高 (非标准式)。

4.如图所示,画△ABC的一边上的高,下列画法正确的是( )。 (非概念变式)

过程性变式使得数学活动实现有层次的推进,而问题变式则等待学生循序渐进地加以解答。通过概念的形成或问题解决的层次,形成一个有层次的活动经验系统,进一步帮助学生理解知识的不同组成部分和完善知识结构。

例如,“解一元一次方程 (1)——合并同类项与移项”的作业可以设计这样一组练习：

解方程：

(1)x+3x-2x=4(负系数)

(2)6y-1.5y-3.5y=3(小数系数)

(3)13x-15x+x=-3(合并后系数为负)

(4)5y+10y-6y=15-21.5(常数项也需合并)

四、设置拓展性问题，培养创造性思维

对中美学生数学学习状况对比的相关数据进行分析,反映的结果表明：中国的教学在培养学生的常规策略上,效果较好；美国的教学在发展创造性数学思维上,较为有效。对此,教师要继承和发扬传统教学的优秀经验,同时也要注意发展学生的创造性数学思维。在课堂教学中,应要求学生进行“自主、合作、探究”学习,在课外作业中也应适当增加知识探究题、解决应用题、开放题的比例,由此,使学习过程变得更具有挑战性,并且通过解决开放性问题,提高学生对创造性问题的解决能力。

例如,在“勾股定理”的作业中,设置应用题：甲、乙两位探险者到沙漠进行探险,没有了水,需寻找水源。为了不至于走散,他们用两部对话机联系,已知对话机的有效距离为15千米,早晨8∶00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10∶00,甲、乙二人相距多远,还能保持联系吗？

再如,在“分式方程”的作业中,设计开放性习题：请联系实际,编写一道关于分式方程的应用题。

五、优化作业设计，实现合理的学习评价

许多人将“学习评价”视为各类测验和考试,实际上,评价的种类是多样的,对学生而言,常用的评价有课堂评价、作业评价、考试评价等。因为课堂时间的限制,课堂评价无法做到每一个问题对每一个学生都作出评价,而考试评价过分强调“甄别”的功能,考试周期较长,一张试卷的容量有限。这使得“课堂评价”和“考试评价”都无法全面、及时、细致地反馈学生的学习信息,而作业评价能弥补以上不足。

作业评价相对考试评价而言有方便、快捷的优势；相对于课堂评价,问题的覆盖面广,能兼顾每一个学生。通过“分层优化作业”,能帮助学生较准确地了解自己学习的不足,有针对性地补缺,补漏。教师能根据学生的作业较准确地进行判断：哪些知识点掌握不到位；学生的薄弱点是识记、理解还是能力；学生的学习态度是否积极等,以便根据学生的学习情况对教学适时进行调控和改进,以取得更好的教学效果。

综上所述,对作业进行分层、运用变式进行优化,能提高教学效率,减轻学生的负担,既继承了中国数学教学的优秀经验,又兼顾了西方教学中对创新能力的培养。

[1]教育部.全日制义务教育数学课程标准(实验稿)[S].北京：北京师范大学出版社,2002.

[2]房维刚.提高复习效率的关键是习题选讲[J].中小学数学,2006, (12).

[3]潘学英.作业批改小贴士[J].黑龙江教育(小学版),2006,(Z1).

[4]徐连红.新课改理念下的数学课堂教学策略[J].上海教育,2003, (15).

[5]江燕.教学交往在数学课堂教学中的实施策略[D].武汉：华中师范大学,2006.

（编辑：朱泽玲）

G633.6

A

1671-0568(2015)36-0011-02