利用时滞分割的方法研究系统的稳定性

谢 涛，钟守铭

(电子科技大学数学科学学院，四川 成都 611731)

引理2[2]:假设f1，f2，……，fN:Rm→R的Rm的开子集D上都大于0，则在集合D内的倒凸集合fi，如果满足下列的条件:

利用时滞分割的方法研究系统的稳定性

谢 涛，钟守铭

(电子科技大学数学科学学院，四川 成都 611731)

研究了带有时变时滞的神经网络系统，通过构造新的Lyapunov-Krasovslii泛函，利用时滞的分割方法，倒凸不等式，Schur定理和添加自由权矩阵等方法，依据Lyapunov稳定理论，用线性矩阵不等式的形式，建立了系统的平衡点是渐近稳定的新标准，最后通过实验证明了新标准可以更好的降低了已有结果的保守性.

时滞；神经网络系统；Lyapunov-Krasovslii泛函；倒凸不等式

神经网络的学习以及成为现代计算机研究的主题，由于其在目标识别，联想记忆等等问题上发挥的不可逾越的作用.然而在现实中的研究，研究这者为了得到更多的易于分析的结果，对神经网络的时滞性采取了忽略的方式，可神经网络的时滞性是客观存在的，并且时滞会对神经网络的稳定性产生影响，最终会导致网络构建的失败；由此，近年来许多学者致力于研究带有时滞性的神经网络，并取得了许多很好的结果[1-7].

本文在对时滞变量划分时是采取0≤h1≤h(t)≤h2，结合最近文章才给出的倒凸不等式和Jeson不等式的变形等方法给出了系统的稳定性条件，再通过实例说明了本文获得的结果能更好的降低系统的稳定

性的保守性.

1 时变时滞神经网络模型及相关预备知识

本文考虑由下述微分方程组成的时滞神经网络模型:

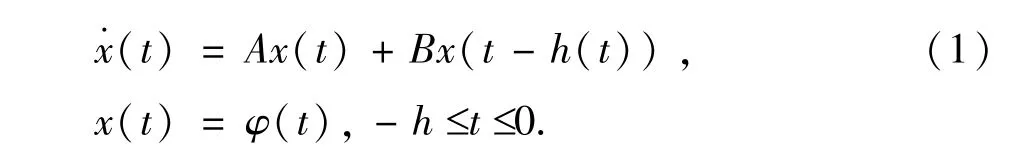
引理2[2]:假设f1，f2，……，fN:Rm→R的Rm的开子集D上都大于0，则在集合D内的倒凸集合fi，如果满足下列的条件:

2 主要结论

定理1:对于给定的常数h1，h2，hd，如果存在适当维数的正定矩阵P＞0，Qi＞0，Rj＞0，Gk＞0，i＝1，2，3，j＝1，2，3，k＝1，2，和具有任意适当维数的矩阵S，F1，F2，K1，K2使下面的线性不等式成立:

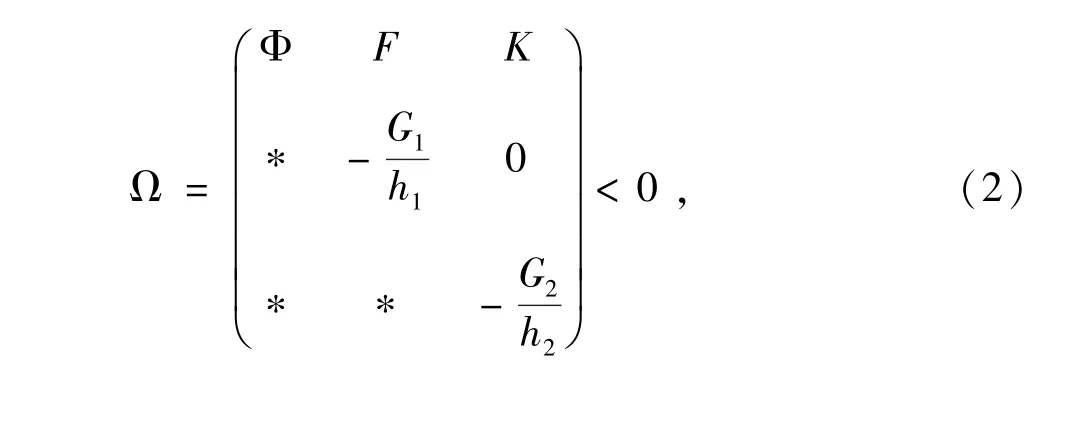
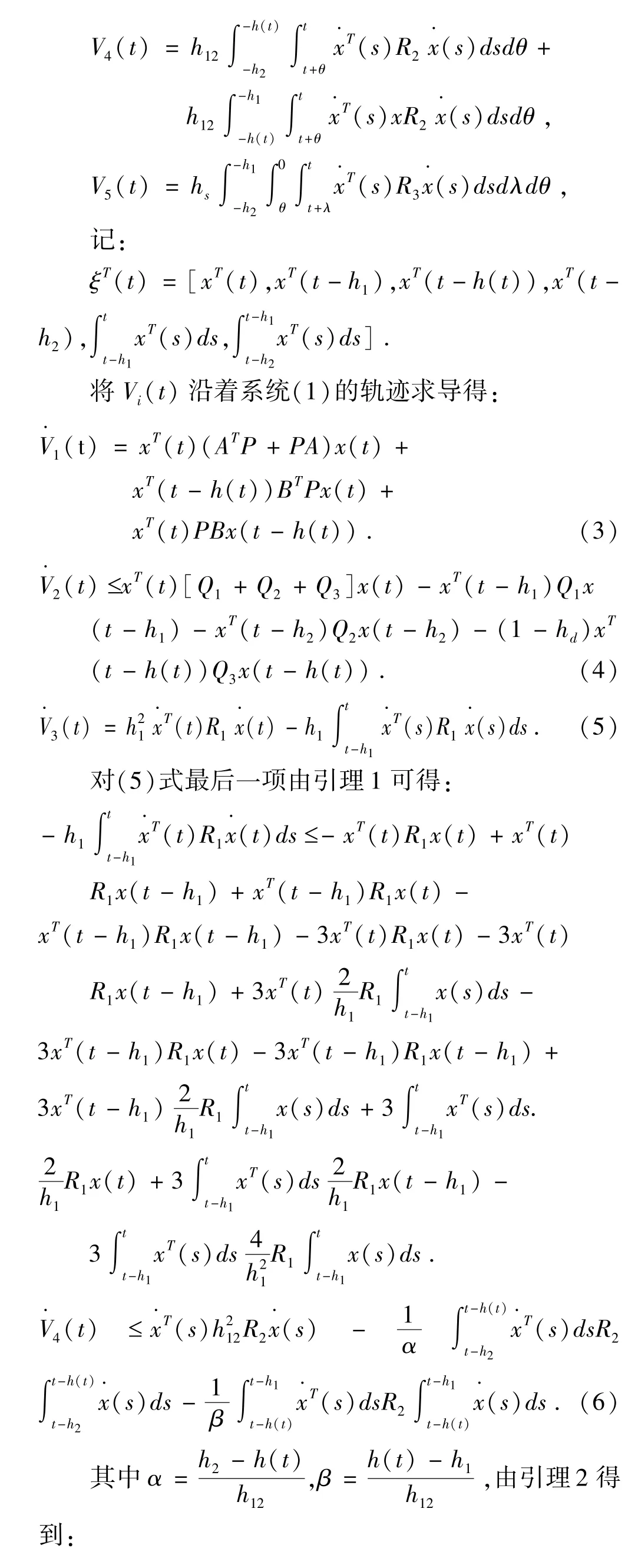
3 数值模拟和分析

例:将系统(1)中的矩阵定义成如下，将A和B代入(3)式，得到两个表:

Table 1是在在不同的hd和h1情况下，h2的最大值得取值情况；从表中可以清楚地看到定理1中所有相同情况下的h2的最大值得取值都比Shao[4]大，特别注意到，在Shao这篇文章中当h1＝5时，已经无法取得相应的h2，而定理1可以取得h2，此时h2＝5.0652；这就说明了定理1可以很好的降低系统的保守性.

表1 在不同的hd和h1情况下，h2的最大值得取值情况Table 1 when hdand h1has different values，the max value of h2can get

[1]SHAO HAN YONG.On stabilization for systems with two additive time -varying input delays arising from networked control systems[J].J Frankl Inst，2012，349(6):2033-2046.

[2]WON IL LEE.Second-order reciprocally convex approach to stability of systems with interval time-varying delays[J].Applied Mathematics and Computation，2014，229:245-253.

[3]O A LADYZHENSKAYA.Boundary Value Problems of Mathematical Physics Moscow:Nauka 1973 English Transl The Boundary Value Problems of Mathematical Physics[M].Springer，New York，1985.

[4[SHAO HAN YONG.New delay-dependent stability criteria for systems with interval delay[J].Automatica，45:744-749.

[5[廖晓昕.稳定性的理论、方法和应用[M].武汉:华中理工大学出版社，1999.

[6]韩伟，王林山.时滞静态神经网络的全局鲁棒稳定性[J].山东大学学报:理学版，2005，40(1):1-16.

[7]刘江.变时滞细胞神经网络稳定性分析[J].数学的实践与认识，2009(15):19-21.

[8]朱培勇，李建.具有时滞的二阶连续型Hopfiled神经网络的周期解[J].西南民族大学学报:自然科学版，2004，30(6):702-706.

[9]瞿杏元，钟守铭.一类带有混合时滞的随机神经网络的全局渐进稳定性分析[J].西南民族大学学报:自然科学版，2012，38(4):550 -553.

[10]董彪，蒋自国.变时滞的双向联想记忆神经网络的全局指数稳定性[J].西南民族大学学报:自然科学版，2011，37(4):521-524.

[11]赵碧蓉，江明辉，沈轶.随机时滞神经网络的全局指数稳定性[J].控制理论与应用，2005(5):799-801.

[12]邱金学.一类时滞系统的稳定性分析及控制器设计[J].纯粹数学与应用数学，2012(03):391-400.

[13]向泽英，钟守铭，罗浩.基于LMI方法的时滞神经网络的全局渐进稳定性分析[J].西南科技大学报，2009，24(1):74-81.

[14]CHEN J，SUN J，LIU GP.New delay dependent stability criteria for neural networks with time-varying interval delays[J].Physics Letters A，2010:191-195.

[15]ZENG HONG BING，HE YONG，Complete delay-decompose approach to asymptotic stability for neural networks with time-varyingdelays[J].IEEE Transactions on Neural Networks，2011:211-217.

[16]CHEN PENG，YU CHU TIAN.Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J].Journal of Computational and Applied Mathematics，2008，214:480-494.

(责任编辑:付强，张阳，李建忠，罗敏；英文编辑:周序林)

Delay decomposition method for stability analysis of systems

XIE Tao，ZHONG Shou-ming
(School of Mathematic Science，University of Electronic Science and Technology of China，Chengdu 611731，P.R.C.)

This paper studies the problem of neural network with time-varying delay systems.It constructs a new Lyapunov functional，and uses delay fine division，lower and upper bounds，Schur theorem and add liberty matrix.Thus，according to Lyapunov stability theory，a new standards is established to guarantee the stability of uncertain delayed neural network.Examples are given to illustrate the conservatism and effectiveness.

time-varying delay；neural network system；Lyapunov-Krasovslii functional；lower and upper bound

O177；TP183

A

2095-4271(2015)04-0485-04

10.11920/xnmdzk.2015.04.017

2015-01-16

谢涛(1990-)，男，汉族，安徽滁州人，硕士研究生，从事神经网络稳定性研究.

钟守铭(1955-)，男，四川成都人，教授，从事动力系统和控制应用研究.

国家自然科学基金资助项目(61273015)