MX(M＝Fe、Ru、Co和Rh，X＝Si和Ge)合金化合物的热力学性质和硬度的第一性原理计算

饶春泉，张 红，程新路

(1.四川大学物理科学与技术学院，四川 成都 610065；2.四川大学原子与分子物理研究所，四川 成都 610065)

MX(M＝Fe、Ru、Co和Rh，X＝Si和Ge)合金化合物的热力学性质和硬度的第一性原理计算

饶春泉1，张 红1，程新路2

(1.四川大学物理科学与技术学院，四川 成都 610065；2.四川大学原子与分子物理研究所，四川 成都 610065)

基于第一性原理，利用赝势平面波法计算得到了MX型合金化合物的结构性质、弹性性质和力学稳定性.计算得到的MSi/Ge的结构参数和形成焓与实验结果以及其他理论计算结果相吻合.结果表明，MSi/Ge具有热力学稳定性且易于合成.计算得到了了MX型合金化合物的弹性常数、体积模量、剪切模量、杨氏模量、弹性各向同性指标以及泊松比.基于弹性常数，得到了CoSi/Ge和RhSi/Ge的德拜温度-压强曲线.基于计算硬度的半经验模型，计算了该系列物质的硬度.其中，RhSi、FeGe和CoGe具有较高的硬度，较高的弹性模量和较低的泊松比，具有成为超硬材料的潜质.

结构稳定性；弹性常数；硬度DFT

二元过渡金属化合物，特别是过渡金属与硅、锗等形成的B20型晶格结构化合物(空间群为P213)，它们奇特的物理性质化学性质一直是研究的热点.例如，窄空半导(FeSi)[1]，反磁性体(CoSi)，顺磁性金属性化合物(FeGe)等.在这些化合物中，硅化物以其特殊的物理性质(低电阻率，高肖特基势垒，耐腐蚀性，高热稳定性和与硅的兼容性等)被普遍用作欧姆接触、肖特基势垒接触、栅电极、局部互联和扩散势垒等材料[2].早在二十世纪三十年代，Phragmen就提出了FeSi的晶格结构.威夫和默勒通过泡沫衍射法得到了FeSi的晶格常数a为4.467(Å)(发表于Strulcturbericht，2，p.241).之后，Pauling等人用实验与理论相结合的方法对FeSi的结构参数进行了修正，确立了其空间群、电子分布等[3].与此同时，与FeSi结构相类似的其他过渡金属硅(锗)化合物也得到了充分的研究[2]，如表1所示.但是，对于MX型化合物的理论研究还相对缺乏，还没有学者对这些结构的物理性质进行综合性的对比研究.

基于第一性原理，本文系统性的研究了MX型金属化合物的结构性质、弹性性质、形成焓和硬度.主要研究目的有以下三点:首先，对MX型金属化合物的结构性质进行补充，在前人研究的基础上完成对MX型金属化合物结构参数的计算；其次，系统地计算8种MX型金属化合物的弹性性质、热力学性质和硬度；同时，对比分析不同化合物的这些性质的异同；最后，我们希望这种系统分析法的提出和实施，能够对后续研究起到指导作用.作为高硬度材料的MX型金属化合物的硬度研究也应当受到重视.

1 计算方法

基于密度泛函理论的平面波赝势方法，对MX型金属化合物的结构几何优化并计算了它们的热力学性质.采用广义梯度近似(GGA)下的PEB泛函来对体系的交换相关泛函进行描述.同时，采用范德比尔特超软赝势来描述过渡金属和硅、锗元素的交互关系.通过多次试算得到该类型化合物平面波截断能最优值为750eV，布里渊区取样采用Monkhorst-Pack方法且k点设置为10×10×10.结构优化收敛条件如下:(1)最小能量变化小于5×10-7eV/atom；(2)单原子最大压强小于0.01eV/Å；(3)同周期原子位移小于5×10-7Å.

为了研究这些同质多型晶体的广义弹性稳定性，本文通过力压关系计算了这些物质的弹性常数.计算得到的弹性常数应当满足广义稳定性标准，立方晶体的力学稳定性标准如下:

同时，在弹性常数的基础上，根据沃特-罗伊斯-希尔近似(Voigt-Reuss-Hill approximation)，体弹性模量B，剪切模量G，杨氏模量E，弹性各向同性指标A和泊松比v表示如下:

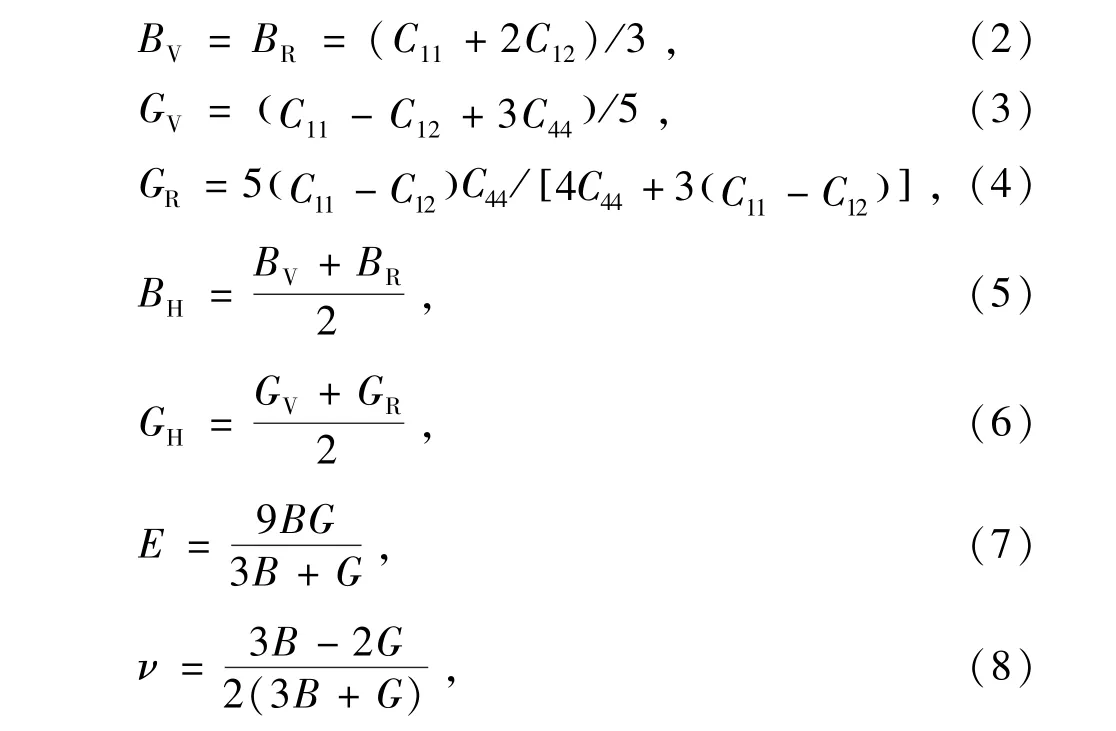
其中，Bv和Gv为Voigt方法下的体弹性模量和剪切模量，BR和GR为Reuss方法下的计算值.另外，形成焓可用以下公式计算(其中M＝Fe，Ru，Co和Rh，X＝Si和Ge):

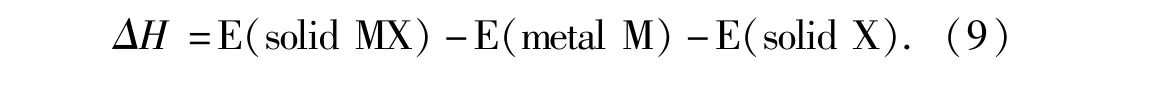
2 结果和讨论

2.1 结构性质

B20型MX立方晶格结构(M＝Fe，Ru，Co和Rh，X＝Si和Ge，空间群为198，P213)，以FeSi为例，可通过Fe和Si沿着＜111＞晶面取代对扭曲氯化钠晶体中的Na和Cl建立模型[12].利用这种模型得到了以上8种物质的晶格结构，计算了各种结构结构性质，并与其他理论和实验数据一并归纳于表1.从表中可知，晶格常数的理论计算值和实验值在误差允许范围内[3].结果表明上述结构模型和理论计算方法是可行的.对比计算值可以发现，晶格常数和密度值随着化合物中金属原子的质量变大而增加，同时MGe的晶格常数和密度值明显大于MSi型化合物.另外，单包体积随压强变化曲线如图1:所有8种结构的体积随着压强的增大都在逐渐减小；在不考虑压强的情况下，Rh/RuX的体积相近，而且随压强的变化趋势也很接近.事实上，这种特殊的性质也表现在Fe/CoX金属化合物中，即相同金属元素的Si和Ge化合物所表现出来的结构性质有惊人的相似.至此，我们认为MX金属化合物的体积与该化合物中金属原子密切相关并随金属原子相对原子质量的增大而增大.

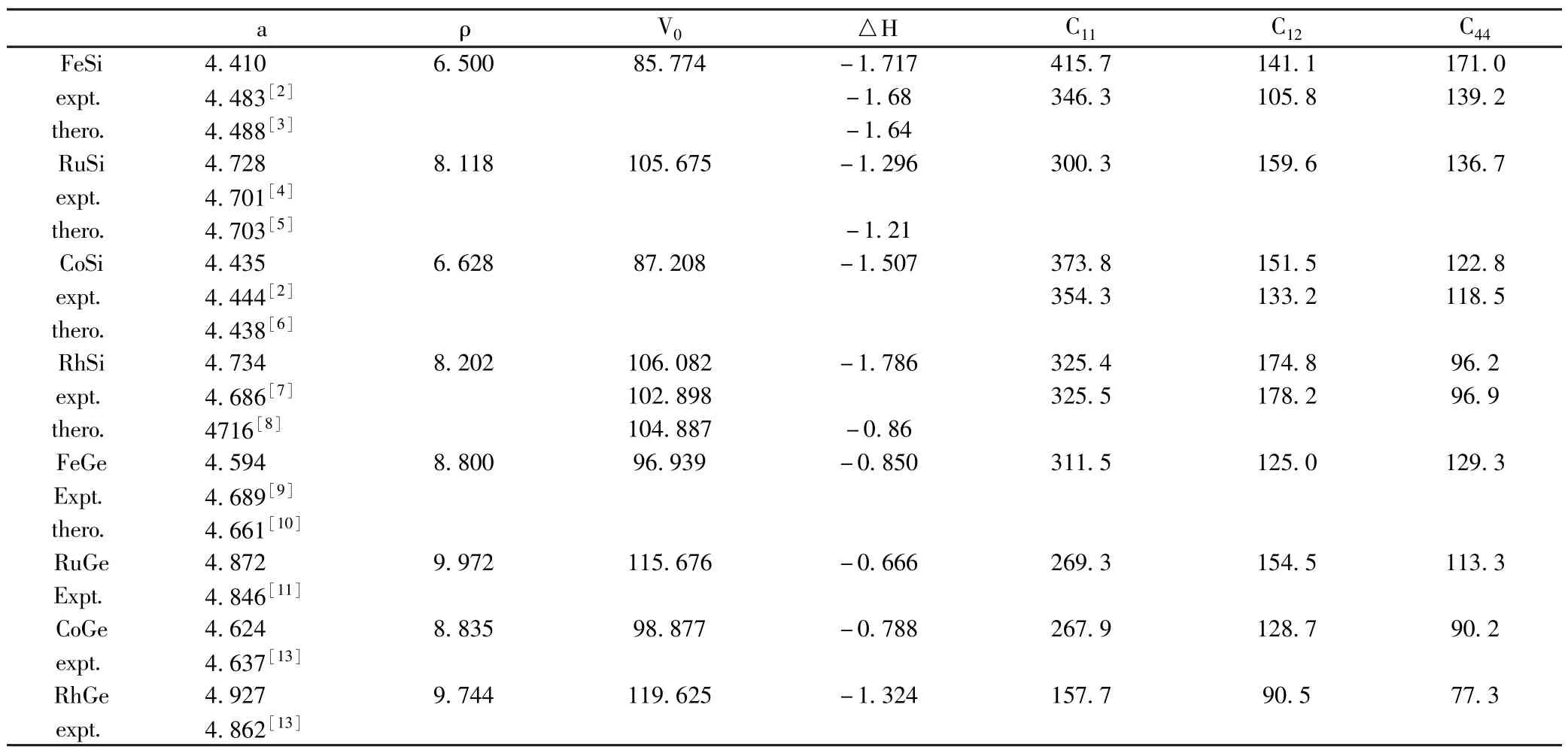
表1 晶格常数a(Å)，原胞体积V0(Å3)，形成焓△H(eV)和弹性常数Cij(GPa)的计算值与文献结果Table 1 The calculated and cited lattice constants a(Å)，primitive cell volume V0(Å3)，formation enthalpy per formula unit△H(eV)and the elastic constants Cij(GPa)for MX intermetallics

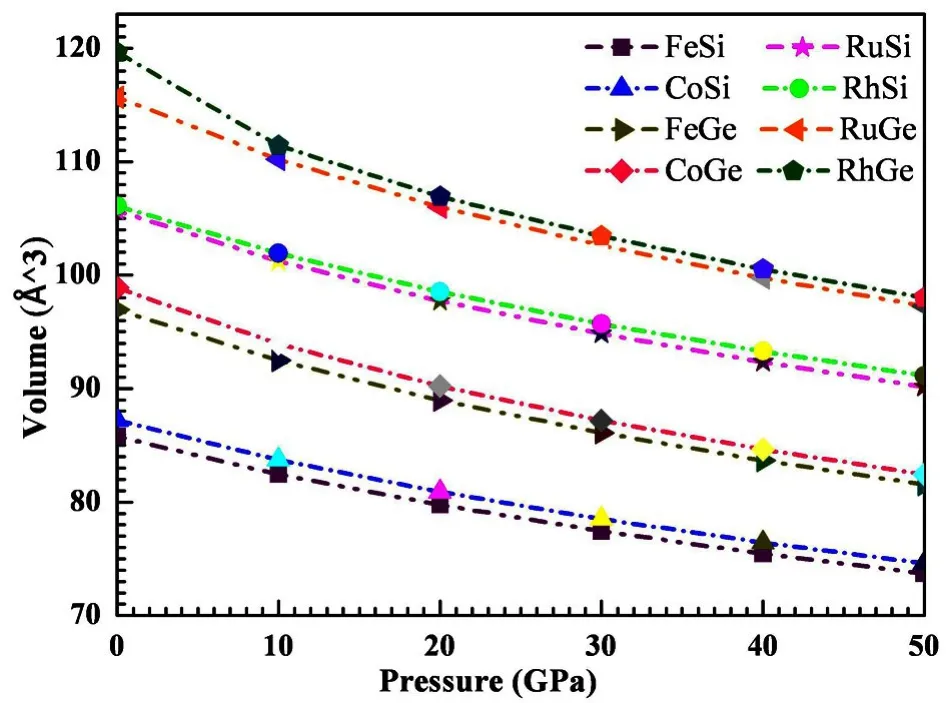
图1 MX型金属化合物原胞体积随压强变化Fig.1 Presure of dependence of the volumes for B20-phase MX intermetallics

2.2 弹性性质和力学稳定性

弹性性质是材料宏观力学性能的一种微观体现.弹性常数的计算结果列于表1.不难验证所有物质的弹性常数都满足力学稳定性判定标准，即表明，这些物质都具有弹性稳定性.对于FeSi、CoSi和RhSi这三种物质，弹性常数的理论计算值与实验值以及其它文献的理论值值的误差在允许范围内，其中以RhSi的相似度最高.但是，对于其他几种NX型金属化合物，本文是首次计算出其弹性常数的.同时我们也希望，我们的研究结果对于后续进一步的探索MX高硬度材料的性质能起到一定作用.

从弹性常数出发，进一步计算出了这些物质的体积模量B、剪切模量G、B/G、杨氏模量E、弹性各向同性指标A和泊松比v，计算结果列于表2.同样，可以发现只有MSi和FeGe的体积模量B有数据可以对比:计算得到的FeSi的体积模量为232.5(GPa)，略小于实验值[5]但是与其他文献理论值误差几乎为零[14]；而FeGe的值187.2(GPa)，则略大于实验值147(GPa)[9]和理论值163(GPa)[10].体积模量和剪切模量的比值B/G用于预测材料的韧性和脆性性质.数值大于临界值1.75的材料较柔韧，小于则较脆.通过表2看到除FeSi和FeGe外的B/G数值均大于1.75，即表明这些物质均较柔韧，而FeSi和FeGe则较脆.相比于其他弹性性质，泊松比v因能描述共价键的定向性而能更直观的展现结构的结合力特征. v＝0.25和0.5分别是中心固力的下限和上限.泊松比同时也能反映晶体对剪切力的稳定性:泊松比越大表明材料的可塑性越好.从下表数据可以看出，除Fe-Si外，其余MX型金属化合物都具有中心固力性.值得一提的是RhSi在MX型金属化合物中具有最高的泊松比v＝0.33，这意味着它有最好的可塑性.材料的弹性各向异性与降低材料微裂痕的可能性存在强相关性，所以弹性各向同性指标A在工程科学中有着重要应用.从表格中可以看出RuSi，RuGe和RhGe具有明显的各向异性，因为它们都有较大的A值，而其余结构则具有相对较好的各向同性特征.

为了研究静水压力对CoSi/Ge和RhSi/Ge系列化合物的影响，本文计算了不同压强下的体弹性模量B，剪切模量G，杨氏模量E和弹性各向同性指标A.结果见图Fig 2(a)-Fig 2(d).可以看到压强对上述性质的影响非常明显，且除弹性各向同性指标A随压强的增大而减小外其余各模量都大体随压强增大而增大，但是体积模量在压强为10-30GPa期间有一个拐点，具体原因我们还没探究出来，希望后续研究者能就这一现象展开深入研究.另外，进一步比较发现，RhGe的剪切模量G和杨氏模量E与CoGe的值很相近.

表2 MX型金属化合物的体积模量B(GPa)，剪切模量G(GPa)，杨氏模量E(GPa)，剪切弹性各向异性系数A，泊松比ν和德拜温度ӨD(K)的计算值和前人结果Table 2 Calculated and cited bulk modulus B(GPa)，shear modulus G(GPa)，Young's modulus E(GPa)，shear elastic anisotropic factor A，Poisson's ratio ν and Debye temperature ӨD(K)of MX intermetallics

2.3 形成焓

为了进一步了解MX型金属化合物的热力学性质，本文计算了它们的形成焓，结果列于表1.形成焓为负值表示该结构具有良好的热稳定性、易合成.从表中可知，在所有计算结果中FeSi和RhSi形成焓最低(分别为-1.717(eV)和-1.786(eV))，这表明它们相比其它MX型化合物具有更好的热稳定性.相对的，RuGe具有最大的形成焓ΔH＝-0.666(eV)，也就意味着它在这些物质中热稳定性最差.

加压可以增强晶体的热稳定性，本文研究了形成焓随压强的变化情况，结果如图4(a).从图中可以明确的看到随着压强的增大形成焓在逐渐减小，表明这些物质的热稳定性随着压强的增大而变好.值得一提的是无论是哪个压强点RhSi都有最低的形成焓，意味着RhSi在上述所有MX型金属化合物中有最好的热稳定性，而RuGe正好有相反的结果.

2.4 德拜温度

作为一个基本参数，德拜温度是一个非常重要的物理量，它和固体的许多物理性例如溶解温度，弹性常数和比热容等密切相关.德拜温度和平均声速vm相关，平均声速可弹性常数数据得到，具体公式如下:

其中，v1和v2是横向速度和纵向速度，可以由纳维方程得到:

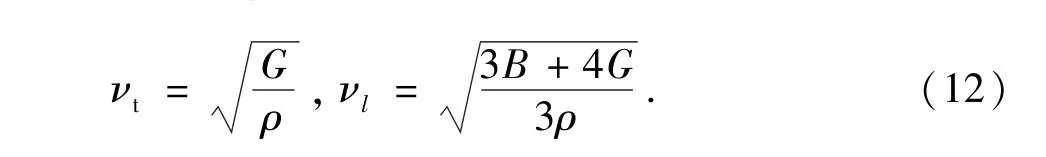
CoSi/Ge和RhSi/Ge在零压和在高压下的德拜温度计算结果列于表2.从表2可知，零压下FeSi和Rh-Si的德拜温度值和前人计算结果非常吻合，但是对于其它MX金属化合物，没有任何理论的或者实验值可以拿来对比.尤其值得一提的是，FeSi的德拜温度比任何其他的计算结果都高.从图3(b)可知，CoSi/Ge和RhSi/Ge系列物质的德拜温度都随压强的增大而

增大.这些物质的德拜温度随压强的变化趋势和剪切模量、杨氏模量随压强的变化趋势基本一致.

图2 MX金属化合物力学参数随压强变化曲线，其中(a)为体积模量，(b)为剪切模量，(c)为杨氏模量以及(d)为剪切弹性各向异性系数Fig.2 Pressure of dependence of the mechanical parameters for MX intermetallics(M＝Co and Rh，X＝Si and Ge)，such as(a)bulk modulus，(b)shear modulus，(c)Young｀s modulus and(d)shear elastic anisotropic factor

图3 MX型金属化合物形成焓和德拜温度温度随压强变化曲线Fig.3 Pressure of dependence of the formation enthalpies and Debye temperature ӨD(K)for MX intermetallics

2.5 态密度

态密度(DOSs)是理解MX结构弹性性质、物理性质和硬度本源的关键因素.CoSi/Ge和RhSi/Ge系列物质在零压和高压下的总态密度(TDOSs)和分波态密(PDOSs)度见图5.在费米面上，如果存在有限的赝势，则该物质表现为金属性.从图5可以看出，Co-Si/Ge和RhSi/Ge系列物质显然都具有金属性.另外，从图5还可以看出这些结构具有一个共同特征，就是存在赝能隙(成键态与反键态的界限)，赝能隙的存在加强了这些化合物的稳定性，且Co/RhSi的雁能隙大于Co/RhGe，即表明Co/RhGe具有更强的共价性.从Co/Rh和Si/Ge的分波态密度图知，在费米能级处电子态密度主要由M-d(Co-d和Rh-d)和X-s.X -p态组成.M-d态与X-s.X-p态表现出了一定的杂化性质，也就是说这些化合物中具有较强的共价键，共价键的强弱对体积弹性模量和剪切模量具有一定贡献.最后，值得一提的是，对于RhSi/Ge体系价带随着压强的增大明显变宽并且转向低能级区域，而导带则转向高能级区域.

图4 MX型金属化合物在零压和高压下PDOSs和TDOSs图Fig.4 Calculated PDOSs and TDOSs for B20-phase MX intermetallics(M＝Co and Rh，N＝Si and Ge)under zero and high pressure

2.6 硬度

理想单晶的硬度正比于键强度和晶体中晶胞的数目，而键强度又正比于键长.通常用重叠布居来直观的表征键强度.因此，通常用密里根重叠布居分析法来计算硬度.根据第一性原理有:

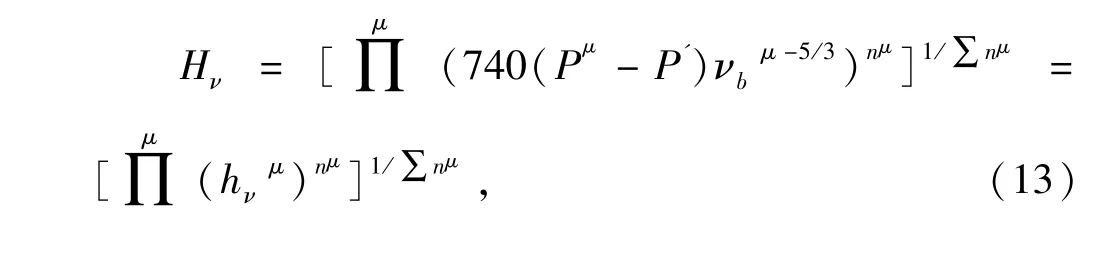
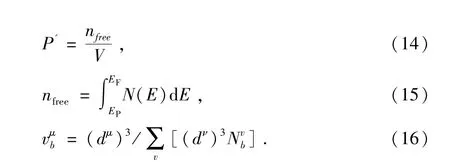
其中，Pμ表示密里根重叠布居数，νμb为体积，nμ为晶体内μ键数量，dμ为键长，Nμb为单位面积的μ键数量，P'为金属布居数，nfree为晶胞内自由电子数目，V为晶胞体积以及EF为费米能.MX金属化合物的键参数和硬度值列于表3，从表3可以看出RhSi、FeGe和CoGe的硬度要明显大于其他几种MX合金化合物.为了研究硬度随压力的变化情况，本文计算了Co-Si/Ge和RhSi/Ge系列物质硬度随压强的变化曲线，见下图5.从图中可以明显的看到，所有物质硬度都随着压强的增大而增大.遗憾的是，对于MSi/Ge系列物质的硬度研究还没有被实验上重视，也希望我们的研究能起到指引性作用.

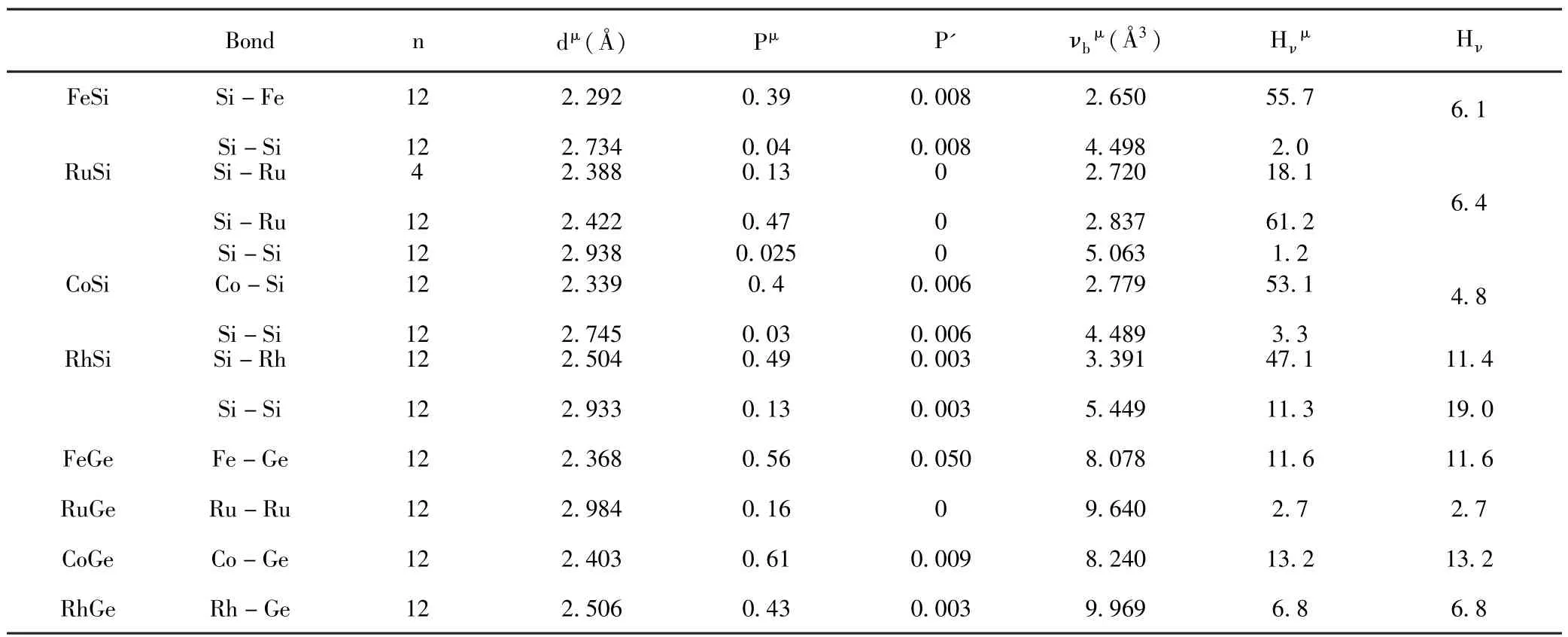
表3 NX型金属化合物的键参数n，键长dμ，密里根布居分布Pμ，键体积νbμ，金属布居P'和维氏硬度Hν(GPa)Table 3 The calculated bond parameter n，bond length dμ，Mulliken overlap population Pμ，bond volume νμ，bthe metallic population P'and Vickers hardness(GPa)for B20-phase MX intermetallics

图5 MX型金属化合物硬度随压强变化曲线Fig.5 Pressure of dependence of the Hardness for MX intermetallics(M＝Co and Rh，X＝Si and Ge)

3 结论

在密度泛函理论的基础上，本文研究了MX型金属化合物的结构性质、弹性性质、力学稳定性和硬度.可以得到以下结论:

1)我们计算得出的晶格参数和形成焓与实验值和文献中理论值非常接近；MX型金属化合物具有良好的热力学稳定性且易合成；随着压强的增大，这些物质的热力学稳定性也随之增大增大.

2)所有MX型过渡金属化合物均具有弹性稳定性.MX型过渡金属化合物的弹性性质受压强的影响都很明显.关于体弹性模量在压强为10GPa-30GPa间的反常现象，希望能得到后续研究者的重视与研究.另外，值得一提的是RhGe的剪切模量G和杨氏模量E与CoGe的值很相近.

3)从弹性常数出发，计算得到了MX型金属化合物的德拜温度，并进一步研究了CoSi/Ge和RhSi/Ge系列物质德拜温度随压强的变化趋势，得到了德拜温度随压强增大而增大的结论.另外，我们还发现这些物质的德拜温度随压强的变化趋势和剪切模量、杨氏模量随压强的变化趋势基本一致.

4)基于第一性原理中有关密里根重叠布居的分析，计算出了MX型金属化合物的硬度，并分析得到了CoSi/Ge和RhSi/Ge系列物质硬度随压强的变化曲线图.通过分析发现所有这些物质硬度都随着压强的增大而增大.

参考文献

[1]KULIKOV N I，FRISTOT D.Influence of disorder on electronic structure and magnetic properties in Fe-rich Fe-Si alloys[J].Computational Materials Science，2000，17:196-201.

[2]PETROVA A E，KRASNORUSSKY V N.Elastic，thermodynamic，and electronic properties of MnSi，FeSi，and CoSi[J].Phys Rev B，2010，82:155124-1-155124-6.

[3]PAULING L，SOLDATE A M.The Nature of the Bonds in the Iron Silicide FeSi and Related Crystals[J].Acta Cryst，1948，1:212-216.

[4]GORANSSON K，ENGSTROM I.Structure refinements for some platinum metal monosilicides[J].Journal of Alloys and Compounds，1995，219:107-110.

[5]IMAI Y，WATANABE A.Energetic evaluation of the semiconducting mono-，sesqui-，and di-silicides of the 8th group elements(Fe，Ru and Os)using first-principle calculations[J].Intermetallics，2008，16:769-773.

[6]SEO K，VARADWAJ K S K.Magnetic Properties of Single-Crystalline CoSi Nanowires[J].Nano Lett，2007，7:1240-1245.

[7]YARMOSHENKO Y M，SHAMIN S N.Valence band spectra of 4d and 5d silicides[J].J Phys:Condens Matter，1997，9:9403-9414.

[8]NIRANJAN M K.First principles study of structural，electronic and elastic properties of cubic and orthorhombic RhSi[J].Intermetallics， 2012，26:150-156.

[9]LEBECH B，BERNHARD J.Magnetic structures of cubic FeGe studied by smallangle neutron scattering[J].J Phys:Condens.Matter，1989，l: 6105-6122.

[10]PULIKKOTIL J J，AULUCK S.Effect of pressure on itinerant magnetism and spin disorder in cubic FeGe[J].J Phys:Condens.Matter，2012，24.096003-1-096003-6.

[11]HOHL H，RAMIREZ A P.Transport properties of RuSi，RuGe，OsSi，and quasi-binary alloys of these compounds[J].Journal of Alloys Compounds，1998，278:39-43.

[12]IMAI Y，MUKAIDA M.Calculation of the density of states of transition metal monosilicides by a first-principle pseudopotential method using plane-wave basis[J].Intermetallics，2001，9:261-268.

[13]LARCHEVV I，POPOVA S V.The polymorphism of transition metal monogermanides at high pressures and temperatures[J].Journal of the Less-Common Met，1982:53-87.

[14]CARACAS R，WENTZCOVITCH R.Equation of state and elasticity of FeSi[J].Gbophyscal Research Letters，2004，31，L20603.

[15]STISHOV S M，PETROVA A E.Self-doping effects in cobalt silicide CoSi:Electrical，magnetic，elastic and thermodynamic properties[J]. Phys Rev B，2012，064433:86.

(责任编辑:张阳，付强，李建忠，罗敏；英文编辑:周序林)

Thermodynamic properties and hardness of MX intermetallics (M＝Fe，Ru，Co and Rh，X＝Si and Ge)from first principles

RAO Chun-quan1，ZHANG Hong1，CHENG Xin-lu2
(1.School of Physical Science and Technology，Sichuan University，Chengdu 610065，P.R.C.；
2.Institute of Atomic and Molecular Physics，Sichuan University，Chengdu 610065，P.R.C.)

Based on the first-principle calculations，the structural properties，elastic properties，mechanical stability，and hardness of MX intermetallics(M＝Fe，Ru，Co and Rh，X＝Si and Ge)are investigated using the pseudopotential plane-waves method.The obtained structural parameters and formation enthalpies for MSi/Ge systems at 0 GPa are well consistent with experimental and other available theoretical data，which indicates that they are thermodynamic stable and can be synthesized easily.Elastic constants，bulk modulus，shear modulus，Young's modulus，shear elastic anisotropic factor，and Poisson's ratio for MX intermetallics are obtained.On the basis of the calculated elastic constants，the pressure-dependent Debye temperature of CoSi/ Ge and RhSi/Ge systems are calculated.Furthermore，the hardness of MX intermetallics is calculated using the semiempirical method.In addition，they are potential hard materials because of the large hardness，elastic moduli and low Poisson｀s ratios.

structural stability；elastic properties；hardness；DFT

O52

A

2095-4271(2015)04-0449-08

10.11920/xnmdzk.2015.04.010

2015-04-06

饶春泉(1980-)，男，汉族，江西人，硕士研究生，研究方向:原子与分子物理；E-mail:xinfangke0219＠126.com

张红(1965-)，女，教授，博士生导师，研究方向:凝聚态，E-mail:xinfangke0219＠126.com

中国国家自然科学基金(NSAF.编号:11176020；编号:11374217)