小波自适应阈值的混沌去噪方法*

张乔斌 位秀雷 刘树勇

(海军工程大学动力工程学院 武汉 430033)



小波自适应阈值的混沌去噪方法*

张乔斌 位秀雷 刘树勇

(海军工程大学动力工程学院 武汉 430033)

为了提高小波分析方法在混沌去噪中的自适应能力,对不同尺度下的小波信号设定调节因子,根据混沌序列关联维的大小确定最优阈值。为了提高寻优效率,采用遗传算法全局自适应搜索最优阈值。利用该方法对Lorenz混沌时间序列进行了去噪分析,结果表明所提方法是非常有效的。

混沌信号; 最优阈值; 小波变换; 去噪

Class Number O322

1 引言

近年来,由确定系统产生的混沌现象在很多学科中得到了广泛应用[1]。但是,由于受到测量工具以及外界环境等影响,实际采集到的混沌信号不可避免地混有噪声,掩盖了混沌信号的真实动力学行为[2]。混沌信号具有功率谱宽带性和似噪声性,其频带与叠加的其他信号的频带往往全部或部分重叠,传统的线性滤波器方法难以实现有效滤波[3]。

小波分析是近些年来发展起来的一种新的时频分析方法,在时频域都有很强的表征信号局部特征的能力[4～5]。用于混沌信号小波去噪的常用方法是阈值法,小波阈值选择会造成去噪信号畸变,选取不当还会造成部分有用信号的丢失,因此,阈值选择是小波去噪效果优劣的关键问题[6]。目前,大多阈值是采用对目标函数估计的方法进行判定[7],不可避免地存在估计误差。考虑到混沌去噪是混沌应用的预处理过程,因此,本文分析了混沌信号噪声水平和关联维的关系,并结合遗传算法,提出了一种全局自适应搜索最优阈值的方法,利用该方法对Lorenz混沌时间序列进行了去噪分析,结果表明所提方法是非常有效的。

2 小波阈值去噪原理

假设实际观测的混沌信号为

x(k)=s(k)+n(k),k=1,…,N

(1)

其中,s(k)表示无噪的混沌信号,n(k)表示高斯白噪声,N表示序列的长度。则小波阈值可按以下三个步骤实现:

1) 对实测信号x(k)进行离散小波变换,得到小波系数wj,k,j,k表示尺度j上的第k个小波系数。

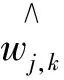
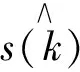
3 信号噪声强度和关联维的关系

噪声通常是由高维动力系统产生,理想的噪声维数维无穷大,混沌系统则产生于低维动力学系统。根据这一性质,可将关联维应用于区分噪声和混沌信号,以实现对噪声的滤除。

文献[8]利用G-P算法计算了4000点的Logistic序列、Lorenz序列、白噪声序列、椒盐噪声序列的关联维数D,结果如表1所示。

表1 不同序列的关联维数

由表1可以看出,混沌序列的关联维相对较小,且表现出分数维,白噪声的值相对较大,由于白噪声序列仍然有可数的项数,得到的序列并不是理想的白噪声,因此关联维仍然存在。而椒盐噪声序列,本身已达到理想状态,因此,不管用多小的In(r),都无法计算出InC(r)随In(r)变化的斜率。以上分析可知,用关联维进行去噪分析具有实际意义。

采样2000点的Lorenz混沌序列s(k)叠加不同强度的噪声,然后计算不同信噪比(SNR)信号的关联维D,结果如表2所示。由表2得知,含噪混沌信号信噪比越大,关联维数越小。在计算关联维数时,需要不断增加嵌入维数以求取饱和的关联维数,这样计算比较复杂,考虑到改变嵌入维数并不能改变序列的相对复杂程度。因此,只求取固定嵌入维数所对应的关联维数来比较就能实现饱和的关联维数在混沌去噪中的应用,从而减少了计算的复杂度。

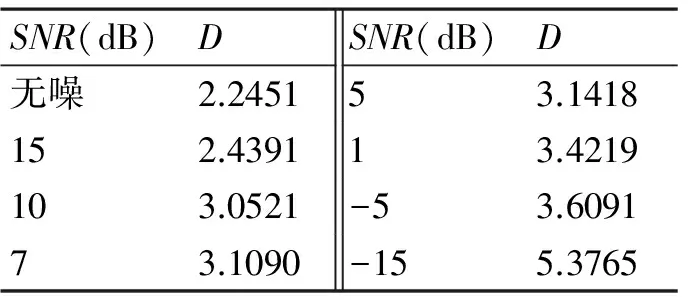
表2 不同噪声强度下Lorenz序列的关联维数

4 小波自适应阈值

在小波去噪中,阈值的选取是一个关键问题,直接影响着去噪效果。阈值选取过高,会过多地将信号当作噪声去掉;阈值选取过低,则保留的噪声信号过多,影响信号的进一步分析。传统的广义阈值去噪方法大都根据噪声能量估计信号信噪比来确定阈值大小,估计过程有一定的误差,其改进的阈值方法也是定量的逼近最优阈值,在小波分解的各个尺度上和最优阈值还有一定的偏差,尚不能实现最优滤波。为了使选取的阈值在各个尺度下都具有最佳的去噪效果,本文利用阈值公式:

(2)

其中,j为小波分解尺度,ti为相应尺度的阈值,N为信号长度,μi为相应尺度调节因子,μi∈(0:0.01:n),鉴于取对数后数值波动较小,因此取步长为0.01,n为正常数,σ为信号在最高尺度上的方差。

调节因子μi的选取根据去噪后序列的关联维数大小进行评定。为了提高最优阈值的搜索效率,本文利用遗传算法进行全局搜索,根据噪声水平和关联维数的关系设定适应度函数为

(3)

由式(3)可以看出,关联维数越小,适应度值越大,说明信号噪声水平越低。

小波去噪过程中,阈值和信噪比(SNR)存在一种单峰规律[9],即阈值从0增加到某一终值时,阈值处理后的结果只有一种是最优滤波。且文献[10]指出,算法终止准则兼顾优质和高效两个方面,若连续迭代最优解的改进程度不明显时,算法终止,否则,进行t=t+1次迭代。

则自适应阈值寻优的步骤如下:

1) 对含噪信号进行j层小波分解,得到小波分解的近似部分an和细节部分d;

2) 保持近似部分不变,对各个细节部分d1,d2,…,dn按式(2)进行阈值量化处理,各尺度的调节因子μi在(0,n)范围浮动,设定浮动步长为0.01;

3) 计算阈值量化后的信号的关联维数D,选取D最小时所对应的阈值t1,t2,…,tn作为最优阈值,其所对应的细节部分为d1,d2,…,dn,对细节部分进行重构,重构后的各个尺度上的信号为d11,d22,…,dnn;

4) 去噪后的信号为:s=d11+d22+…dnn+an。

5 仿真分析

实验信号为Lorenz方程产生的混沌信号,然后叠加白噪声作为有噪声污染的信号进行分析。Lorenz方程:

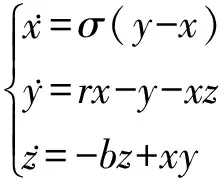
(4)

选取参数的值为σ=10,r=28,b=8/3,用4阶龙格-库塔法进行迭代求值运算,设定积分步长为0.01,删除前6000个暂态点,对其后2000个稳态点进行分析,如图1所示,图1(a)为原始时间序列,图1(b)为信噪比SNR=-8dB时的含噪序列。

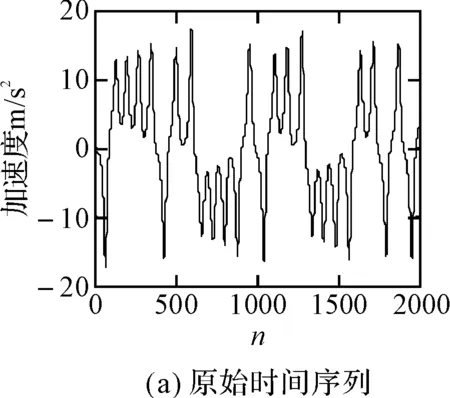
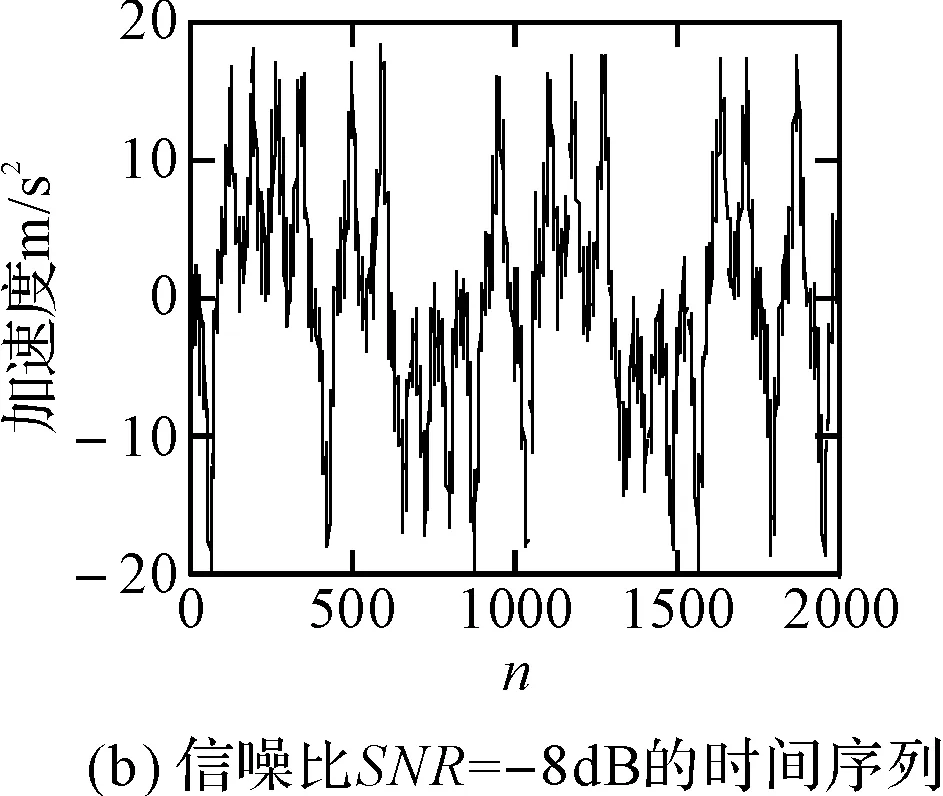
图1 原始时间序列和含噪时间序列

在相空间重构基础上,选择尺度J≤m,m为嵌入维数,τ为重构延迟。m=5,τ=10时,Lorenz系统的混沌特性可以很好地重构于相空间中,因此取J=3,采用正交紧支集(Daubechies)函数的改进小波函数sym8作为小波基函数对混沌序列进行3尺度分解,使用本文方法对每一尺度上的信号进行阈值滤波,其中最小关联维数D=3.06所对应式(5)中的调节因子分别为0.73,1.51,3.37。去噪后的序列图如图2所示,其中‘ⅹ’代表无噪信号,‘-’代表去噪后的信号,可以看出,Lorenz序列和去噪后的序列拟合得很好,证明了本文方法的有效性。

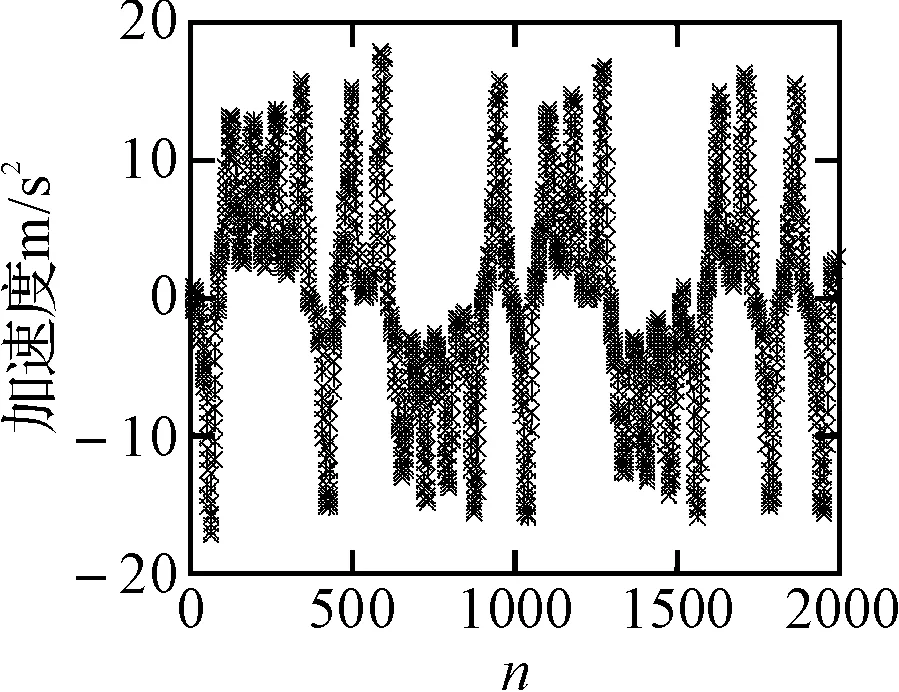
图2 本文方法去噪效果

分别使用广义阈值方法[11]、文献[5]方法和本文提出的最优阈值方法对信噪比为-8dB的混沌信号进行降噪处理,降噪后的信噪比和最小均方误差如表3所示,可以看出经本文方法处理后的混沌信号信噪比最高,最小均方误差最小,表明本文方法能够更加有效地滤除隐藏在混沌信号内的噪声,提高了信噪比,减小了误差,更加适合工程需要。

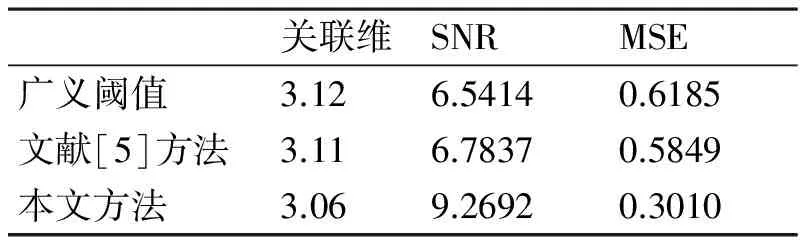
表3 三种方法去噪后结果比较

6 实验分析

文献[12]设计了分段线性混沌振动试验装置,对该系统装置的实测信号利用本文方法进行去噪处理,采用sym8小波基函数对信号进行3层分解,实测信号的关联维数D=3.58,去噪后的关联维数维D=2.78,其中各层阈值调节因子为1.75,2.03,3.85,去噪前后信号的相平面图如图3所示,可以看出,信号中杂波明显被剔除,显示了本文方法的工程适用性。

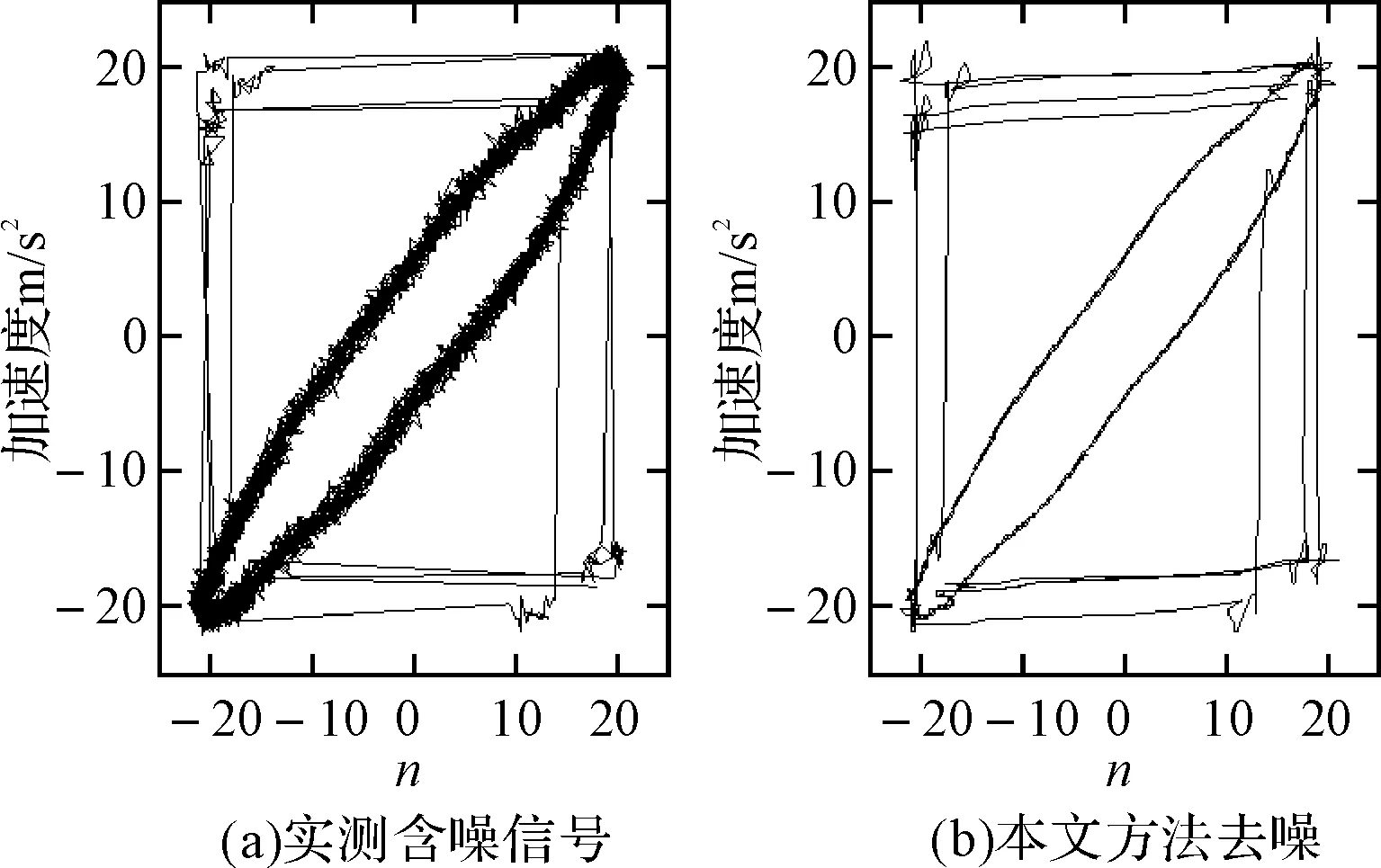
图3 实测信号去噪效果图

图4是实测信号去噪后的最大Lyapunov指数曲线图,信号经本文方法去噪后,减小了干扰对吸引子的影响,恢复了正常的运行轨道,保证了识别的准确性。计算的最大Lyapunov指数LE>0,证实了所测信号是一种混沌振动信号,也验证了实验装置设计的有效性。

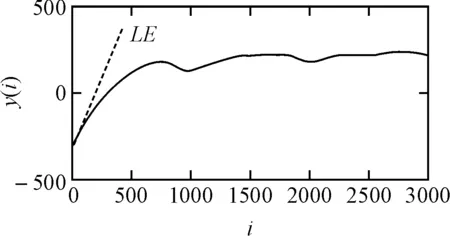
图4 实测信号去噪后的最大Lyapunov曲线图

7 结语

本文简述了小波阈值去噪原理,针对小波去噪中阈值难以有效确定的问题,基于混沌信号关联维数和噪声强度的关系,利用遗传算法对小波信号各个尺度的最优阈值的搜索,克服了以往小波去噪阈值选择的盲目性,实验仿真结果表明该方法能够有效地去除信号中噪声,并保留序列的混沌特性。

[1] Alexander L F, Robin J E. Control of chaos: Methods and applications in engineering[J]. Annual Reviews in Control,2005,29(1):33-56.

[2] Kostelich E J, Schreiber T. Noise Reduction in Chaotic Time Series: A Survey of Common Methods[J]. Physical Review E(S1063-651X),1993,48(3):1752-1763.

[3] Elshorbagy A, Simonovic S P, Panu U S. Noise reduction in chaotic hydrologic time series: facts and doubts[J]. Journal of Hydrology,2002,256(3-4):147-165.

[4] 代海波,单锐,王换鹏,等.基于改进阈值函数的小波去噪算法研究[J].噪声与振动控制,2012,32(6):189-193.

[5] 韩敏,刘玉花,史剑辉,等.基于小波变换阈值决策的混沌信号去噪研究[J].信息与控制,2005,34(5):543-547.

[6] 李树钰.改进的小波阈值去噪方法及其在MATLAB中的仿真[J].噪声与振动控制,2010,2:121-124.

[7] 刘艳霞,刘建军,曹燕燕.一种改进的小波阈值去噪方法[J].河北北方学院学报(自然科学版),2012,28(1):30-33.

[8] 韩贵丞,李锋.一种改进的混沌序列去噪方法[J].信息与电子工程,2011,9(5):586-590.

[9] Li S Y. Improved wavelet threshold denoising method and its simulation suing MATLAB[J]. Noise and Vibration Control,2010,30(2):121-124.

[10] Wang X, Zhao C H, Rong J G. Wavelet thresholding Denoising based on Simplex-Simulated Annealing algorithm[J]. SIGNAL PROCESSING,2008,24(2):242-246.

[11] 吴伟,蔡培升.基于Matlab的小波去噪仿真[J].信息与电子工程,2008,6(3):220-222.

[12] 刘树勇,位秀雷,许师凯,杨庆超.非线性混沌振动响应的试验分析[J].噪声与振动控制,2014,34(2):5-7.

De-noising for Chaotic Signals Based on Adaptive Thresholding Wavelet

ZHANG Qiaobing WEI Xiulei LIU Shuyong

(College of Power Engineering, Naval University of Engineering, Wuhan 430033)

For the purpose of improving adaptive performance of chaotic signals de-noising with wavelet transform, a floating parameter is set to regulate the threshold of wavelet signal on different scales according to the correlation dimension of chaotic time series. The genetic algorithm is helpful to obtain global optimum thresholds and to reduce much time wasted by the adaptive searching computation. De-noising for Chaotic time series generated by Lorenz system is simulated to compare with other methods, and the results showed that the proposed method is effective.

chaotic signal, optimal threshold, wavelet transform, de-noising

2014年9月1日,

2014年10月16日

国家自然科学基金(编号:51179197);海洋工程国家重点实验室(上海交通大学)开放课题(编号:1009)资助。

张乔斌,男,副教授,研究方向:舰船装备综合保障及非线性动力学。

O322

10.3969/j.issn1672-9730.2015.03.015