基于Matlab的水下航行器航向自抗扰控制方法研究*

陈路伟 汤华涛

(1.91388部队93分队 湛江 524000)(2.海军工程大学机械工程系 武汉 430033)



基于Matlab的水下航行器航向自抗扰控制方法研究*

陈路伟1汤华涛2

(1.91388部队93分队 湛江 524000)(2.海军工程大学机械工程系 武汉 430033)

水下航行器航行环境日趋复杂、传统的PID控制日渐无法满足复杂的任务需求,为此论文采用自抗扰控制算法设计水下航行器航向态控制器,以达到替换老旧的PID控制的目的。仿真结果表明,自抗扰控制器操舵平滑,控制速度快,鲁棒性和环境适应能力更好,完全能胜任水下航行器控制的要求。

水下航行器; 航向控制; 自抗扰控制器

Class Number TN95

1 引言

水下航行器的控制模型是非线性的,在水下航行器的运动过程中,模型参数会发生大范围摄动,同时水下航行器的航行环境非常复杂,随着现代海战对水下航行器的操纵性等特性有更高的要求,传统的PID控制方法难以胜任。针对这种情况,国内外很多学者将非线性鲁棒控制、自适应控制、输出反馈变结构控制、模糊控制等现代控制理论与技术应用于水下航行器的控制上,在水下航行器控制方法的研究上取得了一定的进展[1～4]。但也存在一些问题。如鲁棒控制与自适应控制对控制对象的数学模型有较高要求,变结构控制存在高频震颤,模糊控制在工程设计中很直观,但是控制规则的确定和优化比较困难等[5]。这些控制算法由于其本身的复杂性,很多还停留在理论仿真阶段。自抗扰控制技术是一种不依赖被控对象精确数学模型的新型实用非线性数字控制技术,有很好的环境适应能力。它是对经典PID控制器结构方面的缺陷做进一步改进,利用特殊的非线性效应,结合实际的非线性工程算法,是一种自动补偿对象模型的新型控制器[6]。这种估计扰动并给予相应补偿的能力,对于解决水下航行器在运动控制中遇到的各种扰动问题具有一定的适应性。本文拟采用自抗扰控制方法设计水下航行器航向控制的控制方法,以满足其对日趋复杂的水下工作环境的要求。

2 水下航行器的航向控制模型

通过文献[7]可以得到AUV空间运动的完整数学模型。本文研究航向控制问题,AUV模型的水平面运动方程如下:

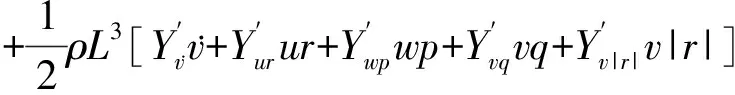
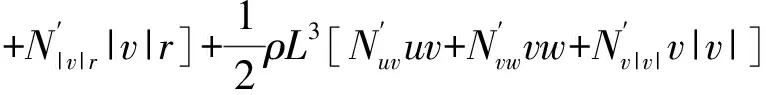
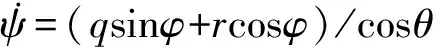
(1)

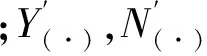
假设UUV的速度稳定于dψ,dv,dr,重心在运动坐标系的原点上,并忽略垂直面运动和横摇运动参数的影响(即认为w,p,q为小量),以及关于v,r的二次非线性项为0,可以得到简化后的AUV水平运动数学模型:

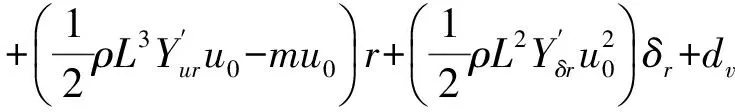
(2)

式中,dψ,dv,dr包括了模型线性近似时产生的误差、不确定性和外界干扰。

因此,可得到UUV航向控制器设计模型:

(3)

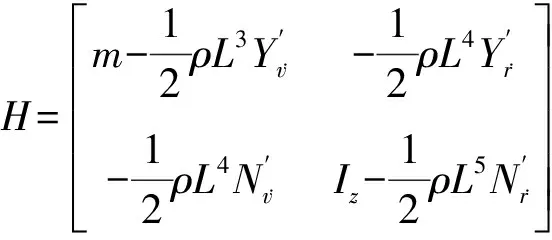
3 自抗扰控制设计

3.1 自抗扰控制器结构及原理

自抗扰控制器由跟踪微分器、扩张状态观测器和非线性状态误差反馈律三部分组成[8]。各个组成部分的作用分别为:跟踪微分器是为系统输入安排过渡过程,得到光滑的输入信号以及输入信号的微分信号;扩张状态观测器是实时跟踪系统状态,不仅能得到系统的状态信息,还能获得对象模型中内扰和外扰的实时作用量。将这个实时作用量补偿到控制器中去,可以使原来的非线性系统变成线性的积分器串联型控制系统。这个动态估计补偿总和扰动的技术是整个自抗扰控制技术中最关键、最核心的技术[9]。非线性状态误差反馈律是把跟踪微分器产生的跟踪信号和微分信号与扩张状态观测器得到的系统的状态估计通过非线性函数进行适当组合,作为被控对象的控制量。

3.2 自抗扰控制器算法设计

将式(3)改写成如下方程形式:

由上式可以看出,v和r是相互耦合的,并且被控量为航向角Ψ,因此在设计自抗扰航向控制器时,忽略有关航速V的方程式,因此有:

令x1=Ψ,x2=r,y=x1,u=δr有:

则可设计扩张状态观测器:

其中β1,β2,β3为自抗扰控制器参数。

则自抗扰控制器为

4 仿真及分析

本文选取某533口径电动力水下航行器在2Kn时的数学模型作为仿真研究对象,模型数据来自文献[10]。就目前而言,PID控制律在控制工程领域占据着绝对主导地位,实际上,水下航行器航向控制器绝大部分还是采用PID。但经典的PID由于对控制系统动态过程的信息利用过少,而且其信息处理的手段过于简单,也存在着缺陷。例如存在调节时间和超调量不可调和的矛盾等。为解决经典PID调节时间和超调量的矛盾,本文采用Matlab中的NCD工具箱对其进行优化。本文选用经过优化的PID控制系统作为自抗扰控制系统的对比仿真研究对象。经过NCD优化过的PID控制器参数为:kp=2.2112,ki=0.04989,kd=0.6438。

利用Simulink建立仿真模型如图1。其中han_td为跟踪微分器离散算法,han_eso为扩张状态观测器离散算法,han_ctrl为非线性状态误差反馈律离散算法,均采用S函数编写。

方向舵角变化范围为-35°～+35°。在仿真时间t=30s时给定一个60°航向角阶跃信号,仿真结果如图2、图3。图3中,实线代表自抗扰控制算法,虚线代表PID算法。由图2可以看出,两种控制方法在正弦输入情况下,均可以较好的完成位置跟踪任务;在阶跃输入情况下,PID控制也可以完成对输入波形的跟踪,但在输入突变的情况下,超调较严重,波动较大,而自抗扰控制基本无超调,波动很小,对干扰的适应性更好。仿真结果表明自抗扰控制可以更好地适应水下航行器的航向控制任务。

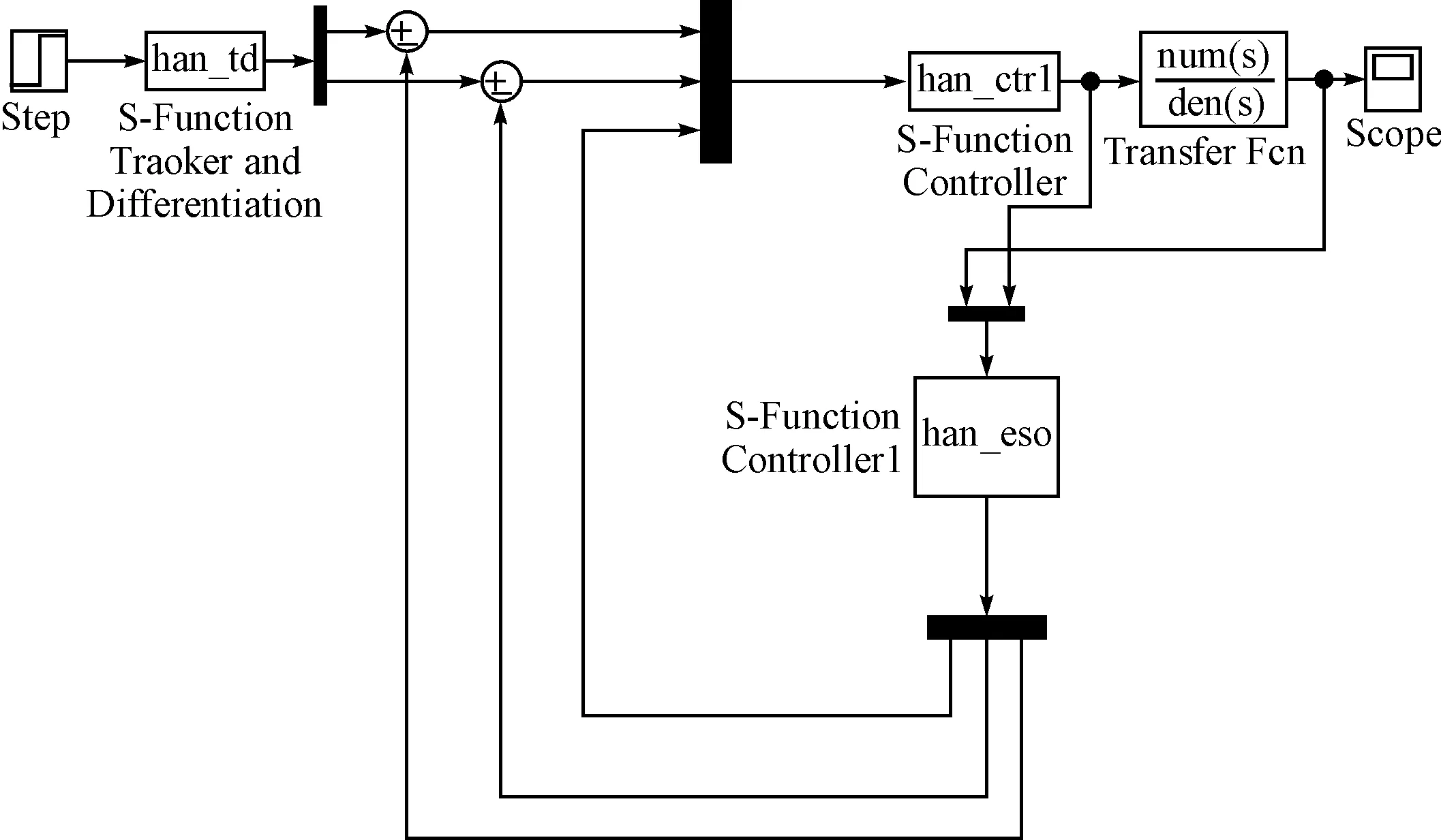
图1 自抗扰控制仿真图

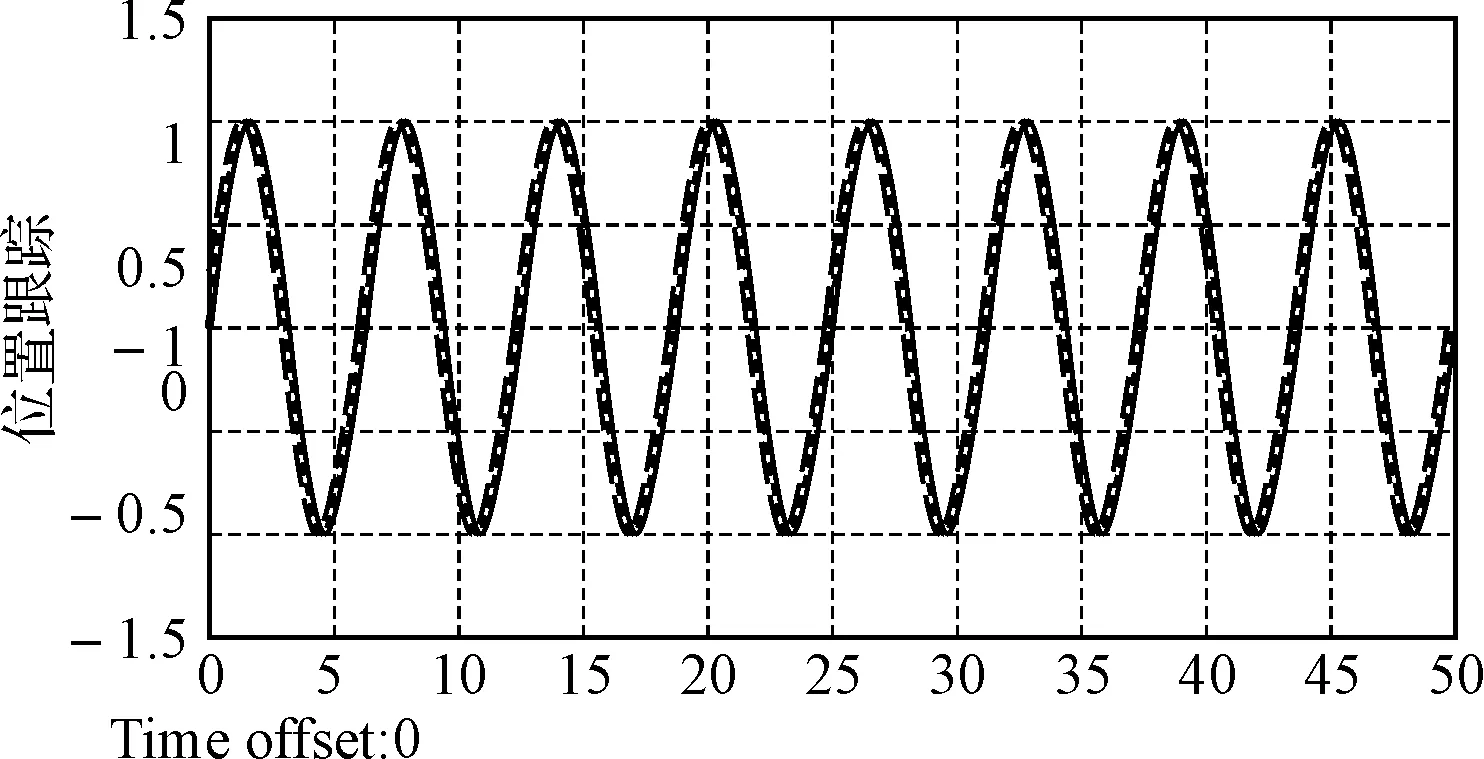
图2 位置跟踪结果

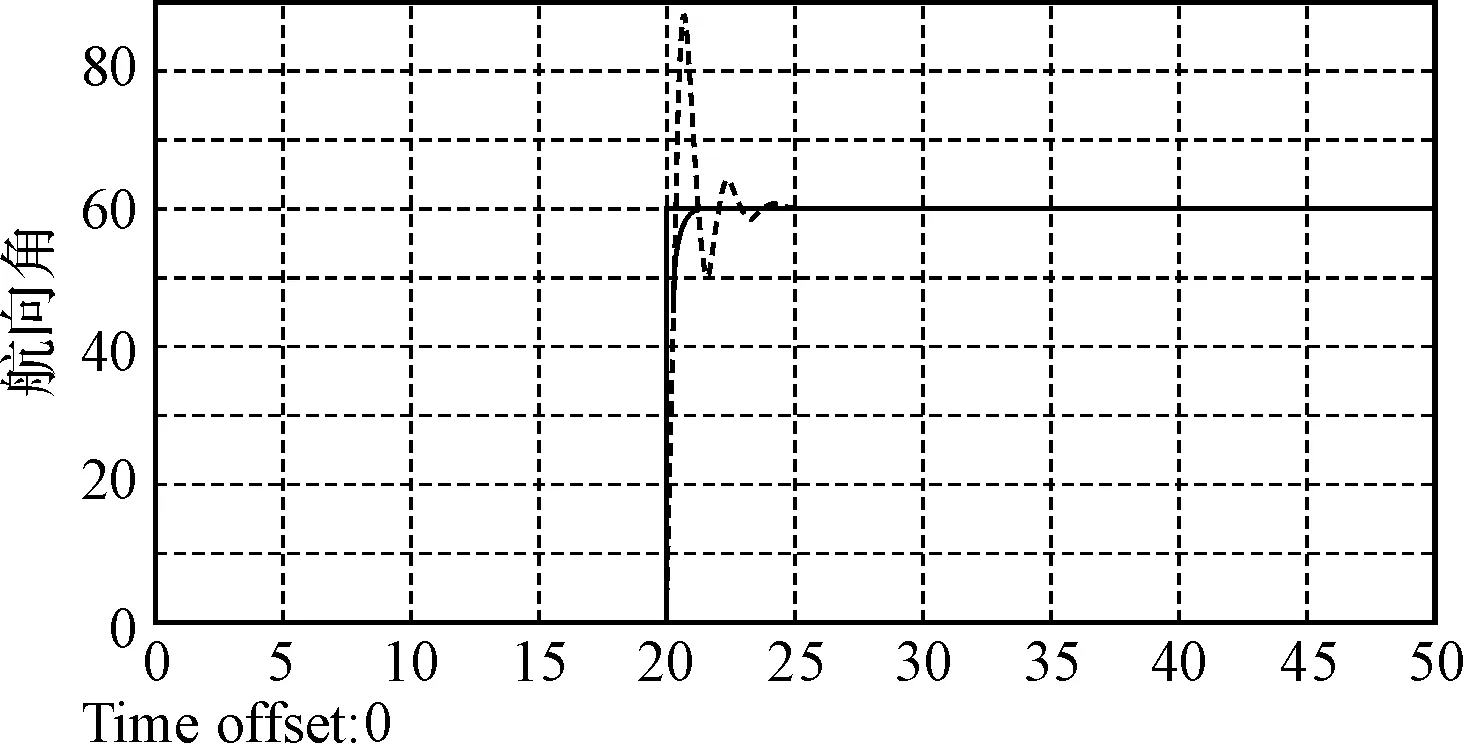
图3 阶跃仿真结果

5 结语

本文推导了水下航行器航向控制的数学模型,并充分考虑了舵机的特性,使被控对象与实际的水下航器动态特性更为接近。在此基础上,采用自抗扰算法设计了水下航行器航向控制器,利用Matlab建立了仿真模型,并同PID控制做了对比性的仿真研究。结果表明,同PID控制相比,自抗扰控制超调小,鲁棒性和环境适应能力更好,完全能够胜任水下航行器航向控制的要求。

[1] 刘正平,徐德民,王晓娟.水下航行体非线性H∞控制研究[J].舰船科学技术,2001,22(7):56-58.

[2] 陈晔,王德石.水下航行体非线性姿态系统的自适应反演控制[J].海军工程大学学报,2008,20(3).

[3] 陈路伟,汤华涛.滑膜控制在水下航行器横滚姿态控制中的应用研究[J].舰船电子工程,2013,33(9):55-57.

[4] Debitetto P A. Fuzzy Logic for DepthControl of Unmanned Undersea Vehicles[J]. IEE. Oceanin Eng,1995.

[5] 陈晔,王德石,董友亮.水下航行体姿态系统的输出反馈变结构控制研究[J].兵工学报,2009,12(8):37-38.

[6] 雷仲谋,吕振铎.非线性自抗扰控制器在航天器姿态控制系统中的应用[J].航天控制,2000(4):34-39.

[7] 李天森.鱼雷操纵性[M].西安:西北工业大学出版社,2005.

[8] 韩京清.自抗扰控制技术[M].北京:国防工业出版社,2008.

[9] 李海生,朱学峰.自抗扰控制器参数整定与优化方法研究[J].控制工程,2004.

[10] 严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005.

AUV Heading ADRC Controller Based on Matlab

CHEN Luwei1TANG Huatao2

(1. Unit 93, No. 91388 Troops of PLA, Zhanjiang 524000)(2. Department of Mechanical Engineering, Naval University of Engineering, Wuhan 430033)

AUV navigation environment is becoming increasingly complex, thus traditional PID control can not meet the growing demand for complex tasks. Therefore ADRC control algorithm is used to design AUV heading controllers to achieve the purpose of replacing the old PID control. Simulation results show that ADRC has steering smooth, controlled speed, better robustness and environmental adaptability, is fully capable of AUV control.

AUV, heading controller, ADRC controller

2014年9月17日,

2014年11月3日

陈路伟,男,硕士,助理工程师,研究方向:水下靶标。

TN95

10.3969/j.issn1672-9730.2015.03.013