双层抽水试验中观测井井筒效应的数值模拟研究

徐 亚，胡立堂，刘玉强，王健媛，董 路，王 琪

(1.北京师范大学水科学研究院/地下水污染控制与修复教育部工程研究中心，北京 100875;2.中国环境科学研究院，北京 100012)

观测井作为地下水环境动态监测的主要手段，以及数值模型反演求取水文地质参数和水质运移参数的主要对象，在水文地质学中具有非常重要的地位。地下水观测井可分两类:一类是测压计式观测孔，这类观测孔井径较小(小于1cm)，可近似视为只有一个点与含水层接触，能很好反映接触点含水层的水质和水头情况;一类是常规观测孔，即有限井径观测孔。

常规观测孔井筒的存在，相当于在含水层中制造出一个具有很大垂向渗透系数的“管道”。在存在三维流的单层含水层系统中，这个“管道”内部会产生垂向的水流，而井筒内部水流的垂向流动又会导致井周水头的重分配乃至对含水层上下部的溶质分布产生扰动。对于井筒穿过二层或以上含水层的观测井，不同含水层之间的水头差在井管内部产生垂向水流将会更加明显，对含水层天然动态的扰动也会更加剧烈。因此，常规观测井的观测数据很难反映实际的地下水水头和水质情况。然而常规观测孔成井工艺相对简单、成本低廉，在很多发展中国家仍大量使用。即使在发达国家，大量历史的水位和水质数据都是通过观测井获得，因而有必要对常规观测井的井筒效应开展“定量”研究，分析观测数据的可靠性及适用范围。

Bennett和Patten［1］等人首先提出了观测井中存在的竖直流问题。Giddings［2］分析了观测井滤管长度对水质采样的影响。Church和Granato［3］通过分析同一场地的测压计式观测井和常规观测井数据，从实践上证实了常规观测井可能导致的观测误差和对周边流场的影响。国内学者陈崇希等人［4～6］提出了双重介质模拟的等效渗透系数法，并基于该方法建立了单层抽水的观测井-含水层耦合模型，定量分析了观测井井筒存在对含水层天然流场分布的影响，并对井筒效应的各影响因素进行了敏感性分析。

实际上，单层抽水是最简单和最基本的井筒-含水层系统。大多数情况下，含水层系统由两层或两层以上的含水层组成，含水层之间由渗透系数相对较小的弱透水层或隔水层分隔，形成多层含水层系统。在实际的开采作业中，抽水井通常穿过多层含水层以增大井孔涌水量，这即是混合抽水。鉴于混合抽水的普遍存在性，有必要对此种情形下观测孔中的水位及其井筒效应进行分析。本文将借鉴陈崇希等人耦合模型模拟的基本思路和分析方法，建立有代表性的混合抽水概念模型，分析混合含水层情景下观测井井筒对地下水天然流场的扰动效果，并对井筒效应的各影响因素进行了敏感性分析。

1 理论介绍

抽水井附近非达西流模拟思路可分为两种［7］:第一种是用一个水流控制方程同时描述达西流和非达西流问题。最典型的方法是陈崇希等人的等效渗透系数法［8～11］，基于管流的能量损失方程，将井管中的水流运动方程改写成达西渗流方程的形式，从而将井孔和含水层统一到一个控制方程下。第二种思路是用不同流态方程描述不同流态区域的水流运动［12～15］，需要解决流态分区以及不同分区边界的耦合问题。

等效渗透系数方法最初由陈崇希提出，最先应用于广西北海市龙潭两层混合抽水试验场［8］求取水文地质参数，随后应用于干旱内陆区地下水系统模拟［9～10］和水平井研究［11］中，并取得了较好的效果。其基本思路是观测井中的管流部分视为渗透系数很大的圆柱形透镜体，并对管流引入形式上服从达西定律的“等效渗透系数”，从而将渗流-管流模型视为含有圆柱形“透镜体”的新的“渗流”系统。对于这个新“渗流”系统，关键问题是如何确定井管的“等效渗透系数”。

流体力学圆柱管中水流的水头损失:

式中:ΔH——水头损失/m;

F——摩擦系数;

l——管长/m;

d——管内直径/m;

u——管内平均流速/(m·d-1);

g——重力加速度/(m·d-2)。

可以分别得到管流为层流和紊流状态时，井管中水流速度的表达式［11］:

井管水流运动为层流时:

井管水流运动为紊流时:

式中:v——流体的运动黏度/(m2·s-1);

μ——流体的动力黏度/(Pa·s);

J——水力坡度;

γ——流体的重度/(N·m-3)。

因为对于井管而言，孔隙度n=1，因此井管内的“渗透流速v”等于实际流速u。将式2和式3与达西定律比较分别得到管流中等效渗透系数的表达式［11］:

观测井-含水层系统的水流运动可耦合为一个方程，即承压水非稳定运动的基本微分方程［12］:

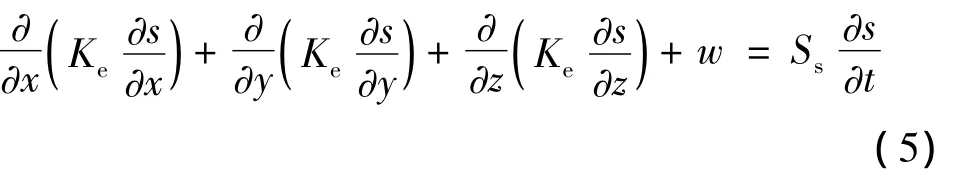
式中:s——(x，y，z)处水头降深/m;

W——源汇项/(s-1);

Ss——比弹性储水系数/(m-1)。

2 案例分析

2.1 模型场景

混合抽水含水层系统由2个及以上的含水层组成，本文仅考虑较简单的双层抽水情景。典型的双层抽水情景可概化如图1所示。整个系统包含1个有限井径的完整观测井、2个承压含水层与1个弱透水层。同时为模拟自然界中普遍存在的三维流，在含水层中心设置一个非完整抽水井，抽水井以定流量Q抽(注)水，从而在含水层中形成垂向分流速的水流。本文的目的就是研究加入观测井前后，观测井内及其附近局部区域内水头和流场的变化。

2.2 控制方程和定解条件

以抽水井与第一层含水层顶板的交点为坐标原点，抽水井与观测井连线方向为x坐标轴方向，竖直方向为z轴方向，水平面上x轴的垂向方向为y轴方向，建立坐标系统如图1(a)所示。此时混合抽水含水层系统中的水头降深可以用式(4)～(5)描述。

图1 概念模型及坐标系统示意图Fig.1 Conceptual model and coordinate system

初始时刻含水层各处降深为0，第一含水层顶板和第二含水层底板均为隔水边界，水平方向上假设模拟时段内水头降深为0，因此混合抽水含水层系统模型的初始条件和边界条件表示为:

式中:S0(x，y，z)——表示模拟区域初始时刻的降深/m;

Sout(t)——表示模拟时段内模型外边界上的降深/m。

2.3 含水层和抽水井参数

含水层系统如图1所示，由两个含水层和1个弱透水层组成，各层均为均质各向同性介质，其渗流参数取值采用参考文献［14］(表1)。抽水井为非完整井，滤管设置在第二含水层顶部，长度为抽水井总长度的1%。

表1 模型基本参数Table 1 Value of basic model parameters

2.4 网格和时段剖分

在抽水初期，含水层水头降深随时间变化很明显，随着抽水继续进行，一段时间后，含水层中的降深变化逐渐放缓。为此，设置初始时间步长为0.001 d，变时间步长因子为1.05，模拟时间步长为127，总模拟时间10.289d。此时含水层中水头变化很小，降深相对变化率小于5‰/d:

式中:ΔSt——表示某一位置处的降深相对变化率/(d-1);

St——某一位置处t时刻的降深/m;

St+1——某一位置处t+1时刻的降深/m。

平面上采用不等距的结点设置，结点距随着与抽水井的径向距离增大而增大，x轴向总计设置49个结点，其中径距小于40m的结点21个。垂向上，设置了46个不等距结点，其中1～21和26～46结点所在层为含水层，21～26结点所在层为渗透系数相对较小的弱透水层(隔水层)。单层结点个数为289个，单层单元个数为584个;整个模型结点数为289×46个，单元数为584×46个。

2.5 模拟结果

利用数值法(平面上基于伽辽金有限单元法，垂向上基于有限差分法)对上述模型进行求解，并基于Fortran平台编制了程序代码。图2为距离抽水井不同位置处，水头降深的分布。从图中可知，在模拟时段末，距离抽水井10 000m处水头降深为零，可推断模型边界处降深也应为0，可认为外边界没有对内部流场产生影响，边界范围的设定是合理的。

图2 模型顶层不同径距处水头降深分布Fig.2 Drawdown distribution in different distance at the top layer

2.5.1 井筒内降深和流量分析

从图3可以看出，观测井井筒中不同深度处降深不同，底层降深小，顶层降深大;顶底层的降深差随着井径增大而减小，如图3(a)中井径为0m的观测井，其含水层顶板和底板的降深差为6.31m，相对应的井径为0.02、0.05、0.1和0.2m 时，降深差分别为6.19、5.23、2.18和0.15m。顶底层的降深差随着径距增大而减小，如图3中井径为0.1m的观测井，位于2.18、4.47、38.53和79.98m位置时，井筒内顶底板间的降深差分别为2.18、1.78、0.42和0.13m。

图3 双层含水层中，观测井井筒内的水头降深Fig.3 Drawdown in the wellbore of observation well in double－aquifer system

在含水层中存在三维水流时，同一水平位置不同高度处存在着水头梯度，含水层底部水头高，越往上水头降深越大，水头越小。若在某一位置处插入一口观测井，相当于增大了此处的渗透系数，在垂向水头梯度的作用下，地下水从高水头水往低水头处流动，在井管内形成明显的垂向水流。根据达西定律垂向水流的流量表示为:

式中:J——相邻井节点间的水力梯度;

Ke——管流等效渗透系数/(m·s-1)，根据式(4)求得;

dw——井筒直径。

由此计算得到的井管内部垂直向上的流量分布如图4所示。

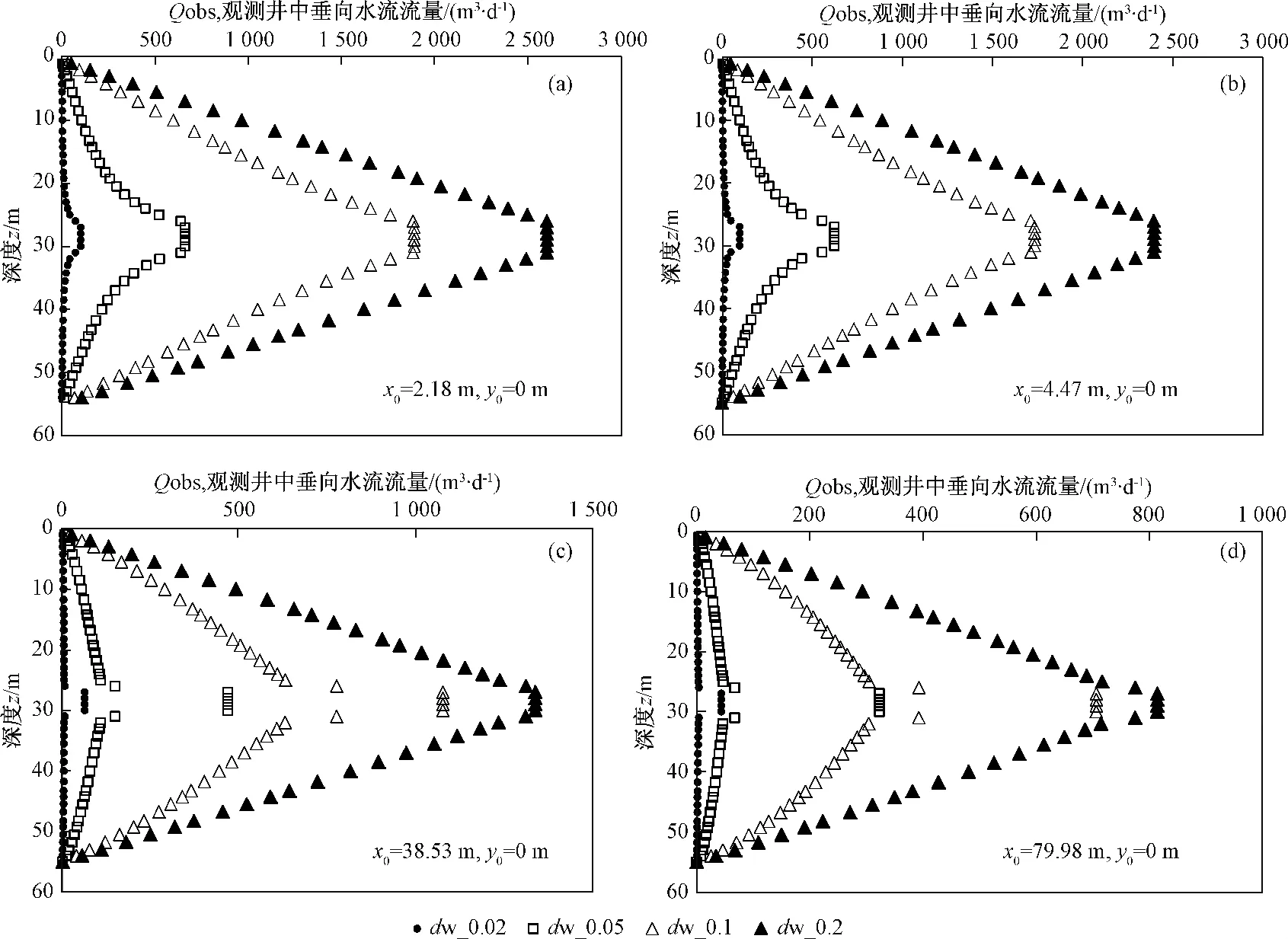
图4 双层含水层中，观测井井筒内的垂向水流Fig.4 Vertical flow in the wellbore of observation well in double－aquifer system

若假定流过任意井单元上的垂向流量为Qup_e，流过该单元相邻的下单元的垂向流量为Qlow_e。则流量经过该单元的增加值为Δ Q。令单位长度上垂向流量的增值为，则:

式中:L——单元上下结点间的结点距。

显然，观测井内单位长度上垂向流量的增值即为该深度上含水层对观测井的水平补给量(若增值为负则为观测井向含水层的补给值)。图5为观测井径距相同时不同观测井井径条件下，含水层对观测井的补给流量与深度关系曲线。

分析图4可以得出以下结论:观测井中的垂向水流随着井径增大而增大，随着径距增大而减小。同时分析图5可知以中间的弱透水层顶底板为界，弱透水层底板以下含水层对观测井进行补给，弱透水层顶板以上观测井向含水层进行排泄。补给和排泄量也与观测井井径大小有关，井径越大补给量(或排泄量)越大。

2.5.2 井筒效应分析

含水层中加入高渗透性的观测井筒后，井筒内会产生明显的垂向水流，导致井筒周围含水层的水头发生重分布。若定义井径为零时，含水层中任意位置(x，y，z)处的水头降深为S0，安装观测井井筒后该位置处的水头降深为SL，则可认为S=SL-S0为井筒对含水层天然水头分布的影响，将其定义为井筒影响下的降深畸变。图6为模型顶层不同径距处的降深畸变，分析模型模拟结果，可以得到降深畸变的以下规律:距离观测井距离越远，受井筒效应影响越小，降深畸变越小。以位于x=2.18 m处，井径等于0.2 m的观测井为例，从图6中可以看出x=2.18 m，即观测井处降深畸变最大为3.0，距离观测井越远井筒的影响越小，以观测井为中心，观测井两侧降深的畸变近似呈对称分布(距离较远时不对称)。

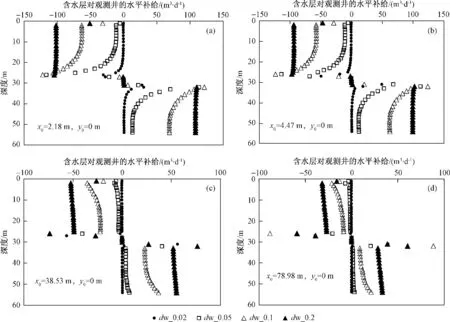
图5 含水层对观测井的水平补给(排泄)Fig.5 Horizontal recharge(discharge)of aquifer to observation well

图6 表层降深畸变沿x轴的分布Fig.6 Drawdown difference along the X axis at the surface layer

井筒效应的影响程度随着观测井内径增大而增大，井径为0.2 m的观测井造成的降深畸变影响最大，井径0.02 m的观测井最小。如图6(a)中，位于x=2.18 m处，井径为0.02 m的观测井井筒中的畸变为0.06 m，而同样位置的观测井，井径为0.05、0.1和0.2 m时，其内部的畸变依次为0.522、1.996和2.99 m，明显呈现随井径增大而增大的规律。

3 结论

(1)在双层含水层中利用不完整井抽水时，同一水平位置不同高度处的水头降深不一样，由此导致的垂直方向的水头差会导致观测井内产生垂向水流，水流的流量受观测井井径和径距影响，井径越大流量越大，径距越大流量越小。

(2)在三维含水层系统中，利用完整观测井在双层含水层中进行水质采样时，采样结果更能代表下方含水层的水质，而对于上方含水层而言不具有代表性。

(3)观测井中的垂向流量会导致井筒周边含水层水头的重分布，此即井筒效应。距离观测井越近，受井筒效应影响越大。

(4)井筒效应的影响程度和影响范围受观测井井径和径距决定，井径越大影响程度和范围越大，径距越大影响程度和范围越小。

［1］ BENNETT G D，PATTENE P.Constant-head pumpingtest ofa multiaquiferwellto determine characteristics ofindividualaquifers［M］. U S:Geological Survey Water-Supply Paper，1962:181-203.

［2］ GIDDINGS T.What is an adequate screen length for monitoringwells:Opinion I［J］. Ground Water Monitoring Review，1987，7(2):96-97.

［3］ CHURCH P E，GRANATO G E.Bias in groundwater data caused by well-bore flow in long-screen wells［J］.Groundwater ，1996，34(2):262-273.

［4］ 陈崇希，蒋健民，林敏，等.地下水不稳定混合抽水的渗流-管流耦合模型及其应用［R］.武汉:中国地质大学(武汉)环境地质研究所，1992.［CHEN C X，JIANG JM，LIN M，etal.Seepageof groundwater pumping unstable hybrid pipe coupling model and its application［R］.Wuhan:Environmental Institute of Geology，China University of Geosciences(Wuhan)，1992.(in Chinese)］

［5］ 陈崇希，胡立堂.渗流-管流耦合模型及其应用综述［J］.水文地质工程地质，2008，35(3):70-75.［CHEN C X，HU L T.A review of the seepage-pipe coupling model and its application［J］.Hydrogeology＆ Engineering Geology，2008，35(3):70-75.(in Chinese)］

［6］ CHEN C X，Jiao J J.Numerical simulationof pumping test in multilayer wells with non-darcian flow in the wellbore［J］.Ground Water，1999，37(3):465-474.

［7］ 徐亚，胡立堂，仪彪奇.井孔-含水层系统数值模拟方法研究进展［J］.水文地质工程地质，2011，38(4):26-29.［ XU Y，HU L T，YI B Q.Advances in numerical simulation methods of a“well-aquifer”system［J］.Hydrogeology ＆ Engineering Geology，2011，38(4):26-29.(in Chinese)］

［8］ 成建梅，陈崇希.广西北山岩溶管道-孔隙-裂隙地下水流数值模拟初探［J］.水文地质工程地质，1998，25(4):50-54.［CHENG J M，CHEN C X. GuangxiBeishan karstpipeline - pore :Groundwater Flow Numerical simulation ［J］.Hydrogeology ＆ Engineering Geology，1998，25(4):50-54.(in Chinese)］

［9］ 胡立堂.干旱内陆河地区地表水和地下水集成模型及应用［J］.水利学报，2008(4):410-418.［HU L T.Integrated model for surface water and groundwater in arid inland river regions and its application［J］.Journal of Hydraulic Engineering，2008(4):410-418.(in Chinese)］

［10］ 胡立堂，王忠静，ROBIN，等.改进的WEAP模型在水资源管理中的应用［J］.水利学报，2009(2):171-179.［HU L T，WANG Z J，ROBIN W，et al.Application ofimproved WEAP modelin water resources management［J］.Journal of Hydraulic Engineering，2009(2):171-179.(in Chinese)］

［11］ Chen C X，WAN J W，ZHAN H B.Theoretical and experimental studies of coupled seepage-pipe flow to a horizontal well［J］.Journal of Hydrology，2003，281:163-175.

［12］ EUNGYU PARK，ZHAN H B.Hydraulics of a finite-diameter horizontal well with wellbore storage and skin effect［J］.Advances in Water Resources，2002，25(4):389-400.

［13］ 万军伟，沈仲智，潘欢迎.水平井的水力特征及其解析解的适用条件［J］.地球科学(中国地质大学学报，2003(5):537-543.［WAN J W，SHEN Z Z，PAN H Y.Hydraulic performance of horizontal well and applicability of its analytical solutions［J］.Earth Science (JournalofChina University of Geosciences)，2003(5):537-543.(in Chinese)］

［14］ HU L T，CHEN C C，CHEN X H.Simulation of groundwater flow within observation boreholesfor confined aquifers［J］.Journal of Hydrology，2011，398(11/12):101-108.

［15］ 徐亚，薛祥山，刘玉强，等.地下水观测井井筒效应的多场耦合数值模拟［J］.地球科学(中国地质大学学报)，2014，39(9):1349-1356.［XU Y，XUE X S，LIU Y Q，et al.A coupled Darcy-Brinkman-NS simulation model of wellbore effect of a monitor well［J］.Earth Science(Journal of China University of Geosciences，2014，39(9):1349-1356.(in Chinese))］