基于弹性补偿法的拱坝极限承载力分析方法

宋 鹏，郑东健，许焱鑫，李季琼

(1．广东省水利水电科学研究院，广东广州 510635;2．河海大学水利水电学院，江苏南京 210098)

目前我国已建成一批300 m级的高拱坝，采用现行的设计规范和工程经验已经无法对这些高拱坝进行安全评价，工程界通常采用拱坝的极限承载力作为拱坝整体安全性能的评价指标(极限承载力为拱坝整体结构完全破坏或变形达到不再适合继续承载时的荷载)。

目前，研究拱坝极限承载力的方法主要包括试验方法、经验判定法以及结合数学理论提出的数值分析法等［1］。在诸多数值分析方法中，以有限元法应用最为广泛。基于有限元法评价拱坝极限承载力的方法有弹塑性分析方法和塑性极限分析方法两种。弹塑性分析方法所采用的破坏模拟方式有失客观性，并且现有的失稳判据都过多地受到人为因素的干扰;而基于塑性极限理论的极限分析由于避免了材料复杂的本构关系以及结构加载路径和加载历史的干扰，只计算结构的极限状态，耗时较少，受到工程界的广泛关注。

进入21世纪以来，基于弹性模量调整策略结合线弹性有限元迭代分析的塑性极限分析方法已被诸多领域所采纳，其中弹性补偿法(elastic compensation method，ECM)［2-6］通过系统地调整弹性模量，将迭代过程中得到的一系列静力容许应力场应用到下限定理中，获得结构的下限极限，将得到的机动许可的速度场应用于上限定理中，获得结构的上限极限。本文根据混凝土及岩体自身的特点，研究了弹性模量调整的策略，提出了基于弹性补偿法的拱坝极限承载力分析方法。

1 弹性补偿法的改进

1．1 单元承载比

在水工建筑物中，结构各部位的工作条件不同，为了满足结构各部分的强度、抗渗、抗冻和抗侵蚀性等要求，以及节省水泥用量和工程费用，通常在水工建筑物的不同部位采用不同性能、不同指标的材料，以便充分发挥材料的性能。为了使弹性补偿法适用于由多种材料组合成的结构，需在应力平均化过程中考虑各种材料的强度参数影响，使得在结构达到极限承载力时每种材料均趋于各自的强度。为此，引入单元承载比［7］的概念，它是一个能同时表征单元内力和屈服条件的综合指标，用于表征离散单元在复杂受力状态下接近于塑性屈服的程度，表达式为

式中:ηe，i为第 i次迭代时单元 e 的承载比;Se，i为第 i次迭代时单元e的等效应力，与材料强度无关;Se，0为第i次迭代时单元e的屈服强度;σij为第i次迭代时单元e的应力分量;σs为单元e的材料强度参数。

混凝土及岩石等准脆性材料，缺乏确切的等效应力和屈服应力。根据Mohr-Coulomb强度理论［8］，材料中任一点的抗剪强度正比于剪切面上的正应力。本文根据Mohr-Coulomb屈服准则定义单元的等效应力，以便将弹性补偿法有效地应用于水工建筑物的极限分析中。

用主应力形式表示的Mohr-Coulomb屈服准则(受压为负)为

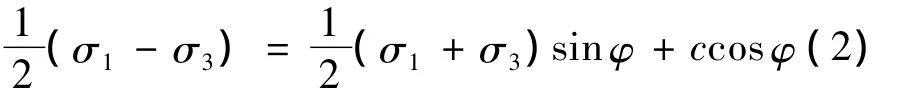
单元的等效应力定义［8］为

取屈服强度 Se，0=c，c为黏聚力。

1．2 承载比均匀度与基准承载比

定义结构的承载比均匀度为

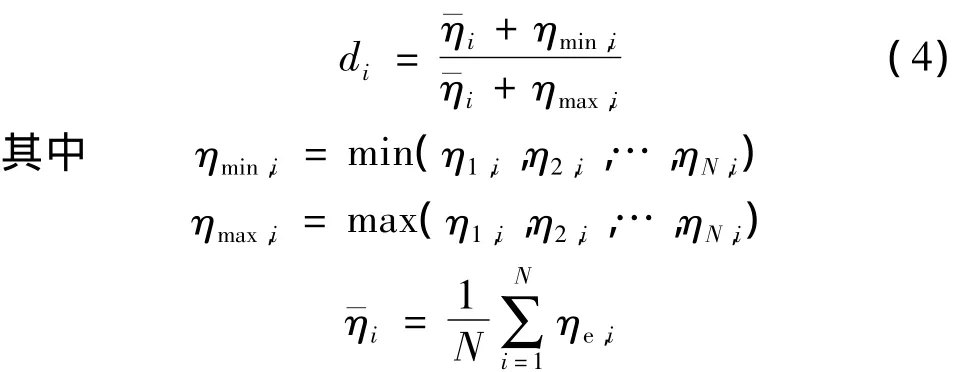
式中:di为第i次迭代计算时结构的承载比均匀度;为结构中单元的承载比的平均值;ηmin，i、ηmax，i分别为结构中单元承载比的最小值和最大值;N为结构总单元数目。

根据单元承载比均匀度，定义基准承载比，并以此作为单元弹性模量调整的阈值:

式中η0，i为结构的基准承载比。

1．3 基于能量守恒原理的弹性模量调整策略

采用单元承载比作为弹性模量调整的控制参数，通过缩减高承载比单元的弹性模量，使得结构中的承载比重分布。假设在第i次迭代调整中，单元e的承载比从调整前的 ηe，i降低到基准承载比 η0，i，与之相对应单元e的等效应力在调整前后分别为ηe，iSe，0及 η0，iSe，0。根据能量守恒原理，弹性模量调整前的单元变形能等于弹性模量调整后的单元变形能与耗散能之和［7］:

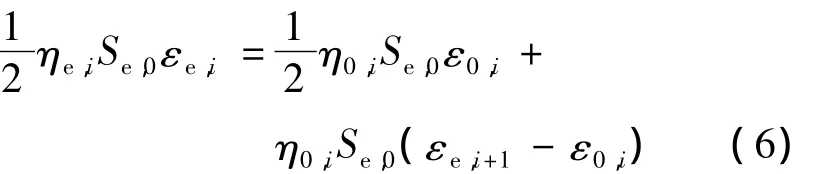
由于计算基于线弹性假设，故单元应力在调整过程中始终满足胡克定律，于是:

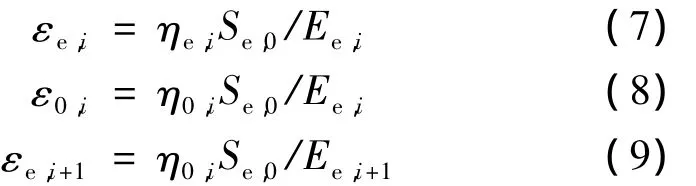
将式(7)(8)(9)代入式(6)，得到第i+1次迭代计算时单元e的弹性模量与第i次迭代计算时的弹性模量的关系为

1．4 改进的弹性补偿法

综合前文内容，以单元承载比作为控制参数，根据承载比均匀度确定的基准承载比，建立一种改进的弹性补偿法。

单元的弹性模量迭代依据下式［5］进行:

当承载比均匀度di较小时，基准承载比较大，弹性模量调整的范围较小;随着迭代的进行，承载比均匀度逐渐变大，基准承载比随之减小，弹性模量调整的范围变大。根据结构中承载比分布的不均匀程度，通过承载比均匀度动态地确定弹性模量的调整区域，能够同时适合于结构局部破坏模式和整体破坏模式，并可以兼顾塑性极限荷载的计算精度和计算效率。

由于在线弹性有限元分析过程中解是线弹性的，第i次计算所获得的最大单元承载比ηmax，i和外荷载之间呈线性正比例关系，那么，塑性极限荷载下限值即可由第i次迭代分析中的荷载基准值和最大单元承载比 ηmax，i来确定［9］:

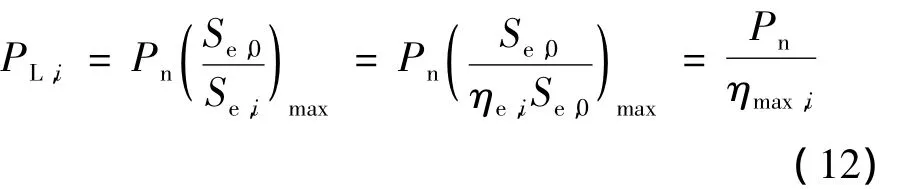
式中:PL，i为第i次迭代计算的下限极限荷载;Pn为荷载基准值。

考虑到对拱坝进行有限元计算时，荷载通常按照体力或面力的方式添加，荷载基准值Pn不易获得精确值，并且按照式(12)计算出的极限荷载来评价拱坝极限承载力也并不直观。因此定义拱坝与基准荷载有关的承载力系数:

以这种方式定义的承载力系数，不仅简洁地反映出坝体的极限承载力，而且避免了荷载基准值计算的烦琐过程，提高了结果的精确度。

重复以上迭代计算，直至满足以下收敛准则:

式中Δ为预设的迭代收敛容差。

若经过n次迭代计算后，计算结果收敛，则根据极限分析下限定理，与基准荷载有关的极限承载力系数:

2 基于改进弹性补偿法的拱坝稳定分析流程

2．1 拱坝稳定分析范围的确定

拱坝与坝基整体失稳机理分析成果表明，拱坝的可能破坏形式有坝体本身的强度破坏、拱坝坝体的屈曲、拱坝沿建基面的滑移、坝肩岩体的滑移和坝肩岩体过大的压缩变形［10］。从已建拱坝来看，影响拱坝整体安全最主要的因素为坝肩岩体的稳定性。拱坝属高次超静定结构，计算拱坝极限承载力的合理方式是将拱坝坝体及坝基系统作为整体来考察。

拱坝坝肩稳定与地形地质构造等因素有关，计算拱坝极限承载力时，需首先确定坝肩滑裂面的位置，然后将坝体连同滑裂面范围内的岩体作为整体计算。根据不同工程滑裂面的产状、规模和性质的不同，可分别按照以下方法来确定可能的滑动面位置:①当坝肩岩体存在明显的连续的断层破碎带、大裂隙、夹层等软弱结构面时，滑裂面由这些陡倾角或缓倾角结构面组成;②当坝肩存在走向顺河流方向及下游斜入河床中的成组节理，并且倾角大致平行于山坡时，滑裂面由这组节理构成;③当坝肩无明显断夹层和节理裂隙，或者节理裂隙不连续、分布又比较均匀时，可先按照弹塑性分析方法对拱坝模型进行试算，将坝体失稳时坝肩岩体的塑性贯通区作为拱坝的可能滑裂面。

2．2 改进的弹性补偿法在MARC平台上的实现

采用大型商用有限元软件MARC来实现弹性补偿法的迭代过程。迭代计算由MARC的两个子程序HYPELA2和 ELEVAR来控制，在分析过程中，HYPELA2主要用来定义用户材料属性，ELEVAR调用单元的有关计算成果。整个迭代过程的流程图1所示。

图1 改进的弹性补偿法算法流程

3 算例分析

3．1 工程概况

某水电站工程属大(一)型一等工程，永久性水工建筑物为Ⅰ级。工程以发电为主兼有防洪等综合利用效益，水库具有不完全多年调节能力。水电站枢纽工程由混凝土双曲拱坝、坝后水垫塘及二道坝、左岸泄洪洞及右岸地下引水发电系统等组成。混凝土双曲拱坝坝顶高程为 1245.00 m，坝基底板高程为950.50m，坝顶长901.771m，拱冠梁顶宽12m，底宽72.912 m，最大坝高294.5 m。水库正常蓄水位1240.00 m，设计洪水位 1238.10 m，校核洪水位1243.00 m，死水位1166.00 m。

该工程枢纽区河谷深切呈“V”字形，两岸平均坡度40°～42°，两岸沟梁相间。根据勘探及坝肩开挖槽地质资料，整个建基面岩体以Ⅱ类岩体为主，在坝基及坝基下游侧靠近坝趾部位的局部地段分布有Ⅲa、Ⅲb及Ⅳa等岩体。此外，在建基面上出露有Ⅲ级断层F11、蚀变岩带(E4+5、E1、E9)及较多的Ⅳ级结构面，它们多属Ⅳb类岩体，随断层破碎带出露的糜棱岩和断层泥多属Ⅳc类岩体。右岸坝基建基面的主要地质缺陷有:Ⅲ级断层F11、Ⅳ级结构面、属Ⅲb类岩体的微风化卸荷岩体和蚀变岩体(E4+5、E1、E9等蚀变岩带)。坝体及坝肩岩体材料参数见表1。

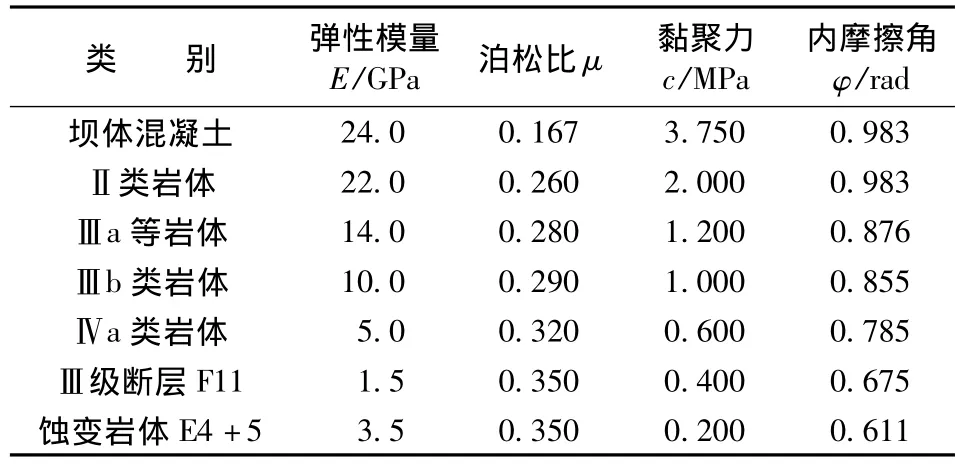
表1 坝体及坝肩岩体材料参数

3．2 有限元模型及荷载工况

选取坝体和一定范围的基岩建立三维有限元模型，边界范围为:以坝轴线为中心，上游侧取1倍坝高，下游侧取1.5倍坝高，坝肩向两岸各延伸1倍坝高，坝基以下取1倍坝高。对铅直基础边界按法向链杆模拟，底部水平基础边界施加全部位移约束，顶部为自由边界。模型充分考虑了坝体的结构特点、河谷地形地貌，模拟了不同岩层分界、风化及卸荷分界、开挖卸荷松弛影响区以及断层等。单元主要采用六面体8节点等参单元。模型共计 113311个单元，122536个节点。图2为坝体及坝基的整体有限元模型。荷载工况为:正常蓄水位+坝体自重。

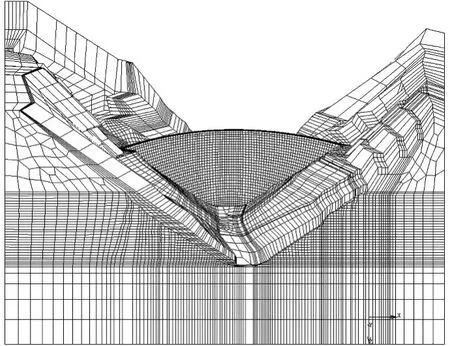
图2 拱坝有限元模型

3．3 极限承载力计算及结果分析

根据工程坝址处岩体地质情况确定坝肩滑裂面，将坝体连同滑裂面范围内的岩体作为拱坝的滑移系统，运用本文所探讨的改进的弹性补偿法计算坝体与基准荷载有关的极限承载力系数。迭代计算中，基准荷载为正常蓄水位坝体所受水压力，收敛容差Δ设定为0.001。图3为承载力系数Ki随迭代步的变化曲线。

由图3可以看出，随着迭代过程的进行，坝体的承载力系数总体上逐渐增大。在迭代进行到第14步时，相邻两次迭代产生的单元最大承载比之差小于设定的收敛容差，迭代过程终止。根据式(15)，该拱坝的极限承载力系数为2.890。由于迭代是基于线弹性的，收敛速度较快，整个计算过程仅耗时1.5 h，充分体现了改进的弹性补偿法算法简单、易于实现、效率高的优点。

图3 承载力系数Ki随迭代步的变化曲线

4 结语

本文结合混凝土拱坝的结构特点，提出了基于Mohr-Coulomb屈服准则的单元承载比计算方法，探讨了通过承载比均匀度与基准承载比调整单元弹性模量的策略，避免了弹性补偿法名义应力确定的困难。应用塑性极限分析方法，提出了基于弹性补偿法的拱坝极限承载力分析方法。工程实例分析结果表明，应用改进的弹性补偿法可以有效地分析拱坝的极限承载力，同时避免了常规分析方法失稳判据确定的困难。

［1］李同春，王仁坤，游启升，等．高拱坝安全度评价方法研究［J］．水利学报，2007，38(增刊 1):78-83．(LI Tongchun，WANG Renkun，YOU Qisheng，et al．Study on safety evaluation methods for high arch dams［J］．Journal of Hydraulic Engineering，2007，38(Sup1):78-83．(in Chinese))

［2］王飞，陈钢，刘应华，等．极限分析的弹性补偿法及其应用［J］．应用力学学报，2004，21(4):147-150．(WANG Fei，CHEN Gang，LIU Yinghua，et al．Elastic compensation method of limit analysis applications［J］．Chinese Journal of Applied Mechanics，2004，21(4):147-150．(in Chinese))

［3］王飞，陈钢，刘应华，等．内压下含局部减薄缺陷三通的极限分析［J］．清华大学学报:自然科学版，2004，44(11):1517-1519．(WANGFei，CHENGang，LIU Yinghua，et al．Limit analysis for piping branch junctions with local wall-thinning under pressure［J］．Journal of Tsinghua University:Science and Technology，2004，44(11):1517-1519．(in Chinese))

［4］YANG P，LIU Y，OHTAKE Y，et al．Limit analysis based on a modified elastic compensation method for nozzle-tocylinder junctions［J］．International Journal of Pressure Vessels and Piping，2005，82(10):770-776．

［5］杨璞，刘应华，袁鸿雁，等．计算结构极限载荷的修正弹性补偿法［J］．工程力学，2006，23(3):21-26．(YANG Pu，LIU Yinghua，YUAN Hongyan，et al．A modified elastic compensation method for the computation of limit loads［J］．Engineering Mechanics，2006，23(3):21-26．(in Chinese))

［6］陈立杰，刘应华，杨璞，等．复杂结构塑性极限分析的修正弹性补偿法［J］．机械工程学报，2007，43(5):187-193．(CHEN Lijie，LIU Yinghua，YANG Pu，et al．Modified elastic compensation method for limit analysis of complex structures［J］．Chinese Journal of Mechanical Engineering，2007，43(5):187-193．(in Chinese))

［7］杨绿峰，余波，张伟．弹性模量缩减法分析杆系和板壳结构的极限承载力［J］．工程力学，2009，26(12):64-70．(YANG Lufeng，YU Bo，ZHANG Wei．The elastic modulus reduction method forload carrying apacity evaluation of frame，plate and shell structures［J］．Engineering Mechanics，2009，26(12):64-70．(in Chinese))

［8］夏志皋．塑性力学［M］．上海:同济大学出版社，1991．

［9］MACKENZIE D，SHI J，BOYLE J T．Finite element modeling for limit analysis by elastic compensation method［J］．Computers ＆ Structures，1994，51(4):403-410．

［10］郑东健，雷霆．基于突变理论的高拱坝失稳判据研究［J］．岩土工程学报，2011，33(1):23-27．(ZHENG Dongjian，LEI Ting．Instability criteria for high arch dams using catastrophe theory［J］．Chinese Journal of Geotechnical Engineering，2011，33(1):23-27．(in Chinese))