水文模型参数敏感性分析方法评述

宋晓猛，张建云，占车生，王小军，刘翠善

(1.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京 210029;2.水利部应对气候变化研究中心，江苏南京 210029;3.中国矿业大学资源与地球科学学院，江苏徐州 221116;4.中国科学院地理科学与资源研究所陆地水循环及地表过程重点实验室，北京 100101)

水文过程是一种受气候、气象、地形、地貌和下垫面等因素影响的复杂自然过程，蕴含着确定性的动态规律和不确定性的统计规律［1］。水文模型则是人们对这种复杂过程的一种抽象化和概念化认识，是通过一些概化的数学公式或物理方程来描述这种高度复杂的非线性的自然过程的一种工具［1-2］。由于对水文过程机理认识不足，导致模型构建过程中存在极大的不确定性，从而影响模型模拟精度和预测结果。而作为建模过程中不确定性的主要来源，模型参数的不确定性是模型不确定性研究的重点内容［3］。一般而言，水文模型参数有数十到数百个，复杂的水文模型可能更多，各参数的不确定性使模型的模拟结果存在很大差异，要同时提高每个参数的精度非常困难，为此，需要定量评估各参数的影响，为实现高效便捷的模型优化和率定提供基础支撑［4］。因此，参数灵敏度分析是模型构建过程中的一个关键环节。

参数敏感性分析的目的在于:①确定哪些参数是对模型输出贡献较大的重要参数;②确定不同参数组合对模型模拟效果的影响，以验证模型参数之间的相互作用;③确定不敏感参数，降低参数率定过程中的计算消耗［5］。目前，敏感性分析已经广泛应用于诸多领域，如系统科学、生态环境科学、经济学、物理学和社会科学等［6-7］，同时形成了诸多方法，如局部分析法和全局分析法、定性方法和定量方法［8］。如何选择合适的方法，怎样合理地应用以及解释分析结果成为敏感性分析应用的关键。为此，笔者拟从敏感性分析的作用与意义入手，对水文模型参数敏感性分析方法进行简要的梳理和总结，探讨敏感性分析的分类方法，进而详细阐述常用的4类敏感性分析方法在水文模型中的应用及各种方法的优劣;从模型参数评价的角度探讨水文模型参数敏感性分析的主要框架，剖析敏感性分析研究的主要不足，并指出今后研究的重点方向。

1 参数敏感性分析的作用与意义

在水文模型的构建过程中，众多的概化(参数化)现象使模型与实际物理过程之间存在差异，同时许多参数无法通过实验手段测试量化，需要采用多种方法率定以期较好地符合实际物理过程［9］。因此，参数的识别、敏感性分析、不确定性分析等参数优化过程是模型构建与应用过程中必不可少的环节。

1.1 敏感性分析与参数识别

由于水文模型结构的复杂性和模型参数在高维空间表现出来的复杂相关性等，直接导致参数的识别问题。参数识别也是参数敏感性分析的一个重要内容，通过定性或定量的手段，分析水文模型参数的敏感性程度，确定参数重要程度，从而实现参数识别，以提高模型参数的量化能力，降低参数维数及模型不确定性，进而提高模型效率，方便模型的应用推广。很多学者针对多种敏感性分析方法开展对比研究，讨论多种方法间的优劣，探讨参数的可识别性及分析的可靠性［10-12］，Castaings等［13-14］指出参数敏感性分析可为模型参数识别与估计提供更多的信息，刘毅等［15］阐述了参数识别与参数敏感性与不确定性之间联系，采用参数敏感性分析方法对模型参数识别提供了深入分析与理解模型系统的有效途径。同时，Rosolem等［16］研究结果显示，单目标条件的敏感性分析可能导致模型参数分析的失当，在应用过程中应考虑多目标响应的影响，能更确切地分析模型参数的敏感性，为模型参数识别和估计提供更高的保证。

1.2 敏感性分析与不确定性分析

一般来说，参数的不确定性依赖于模型结构，并直接导致了参数的敏感性问题，因此，敏感性分析和不确定性分析通常是相辅相成的。不确定性分析侧重于考虑模型不确定性的来源(如模型结构、参数及输入数据等)对模拟结果的影响程度，敏感性分析侧重于考虑模型参数的变异对模型输出结果的贡献率。对参数的敏感性分析和不确定性分析而言，两者在应用过程中往往是相互联系与印证的。如Mishra［17］对比分析了不同不确定性分析方法(Monte Carlo模拟法、一阶二矩分析法、点估计法、逻辑树分析法和一阶可靠性分析法等)和敏感性分析方法(逐步回归分析法、交互信息分析或熵分析法、分类树分析法等)在水文模型中的应用，结果显示敏感性分析和不确定性分析的结果吻合较好，说明参数的不确定性主要源于重要的敏感参数，因此参数敏感性分析和不确定性分析往往需要同步进行，以全面地反映参数的不确定性影响［18］。又如 Beven等［19］发 展 的 基 于 RSA(regionalized sensitivity analysis)法［20］的不确定性分析方法(GLUE法)也被用于水文模型的敏感性分析中;Ratto等［21］将两者联合起来进行模型参数的敏感性分析和参数率定，Elsawwaf等［22］同时评估了多种蒸发计算模型的敏感性及不确定性，指出了两种分析方法的相通性。

1.3 敏感性分析与参数优化

由于模型参数的不确定性普遍存在，根据经验估计或者观测值优化得到的参数并不能保证模型应用的精度和预测结果的可靠性［15］。因此，在追求更加高效和稳定的优化算法的同时，需要分析模型参数的不确定性及敏感性，以确定模型参数优化结果对模型预测的影响。模型参数众多是水文模型应用过程中需要特别关注的问题，在参数优化时往往要耗费较大的计算量，然而通过敏感性分析可以有效筛选重要参数进行优化，提高分析效率，也为模型应用提供基础。如Werkhoven等［23］借助于全局敏感性分析方法作为筛选工具来降低参数维数，进行参数的多目标优化率定，并将其成功应用于SAC-SMA模型;Liu等［24］同样基于上述理念，考虑多目标敏感性分析和多目标条件的参数优化，耦合Morris分析方法和非支配排序差分算法(non-dominated sorting differential evolution，NSDE)用于 MIKE/NAM降雨径流模型的参数敏感性分析和率定。除此之外，还有很多水文模型应用研究在开展参数优化分析的同时进行其敏感性分析，以更有利于参数优化。

2 敏感性分析方法的分类

目前，常见的参数敏感性分析方法分类有以下3 种分法:局部分析法和全局分析法［4-5，25-27］;数学方法、统计方法和图解法［7，28-31］;筛选分析法和精炼分析法［32］，其中第一种分法是最常见的分类方法，且被广泛认可［25］。局部敏感性分析法只检验单参数对模型的影响，简单快捷，可操作性强，曾被广泛应用，但其忽略了模型参数之间的相互作用，而一个参数的不同取值可能会影响另一个参数的敏感度，因此该方法缺乏稳定性。全局敏感性分析法能够同时考虑多个因子对模型输出的影响以及各因子之间的相互作用对模型输出的影响，可全面认识各因子的敏感程度，适用于参数众多的水文模型［8］。全局敏感性分析又可以分为定性全局敏感性分析和定量全局敏感性分析，其中定性分析仅给出各个参数对模型模拟结果的不确定性影响的相对大小，以较低的计算代价得到参数敏感度排序;定量分析是通过计算各参数的不确定性影响贡献率以确定参数的敏感程度，可给出一个具体的量化指标，如一阶敏感度及总敏感度等。

数学方法是通过计算输入变量的变化引起的线性或非线性响应以获得敏感度。通常这些方法不能反映输入方差引起的输出目标变异程度，但可以反映输入变量方差的变化对输出的影响［7］，常用方法有NRSA(nominal range sensitivity analysis)法和DSA(differential sensitivity analysis)法。统计方法则是假定参数满足某一概率分布，基于参数样本评价参数输入的方差对输出分布的影响，可以同时考虑多个参数的变化，且可识别出多个参数之间的相互作用对输出的影响。统计方法的关键在于参数取样方法，最常用的有蒙特卡洛法、拉丁超立方抽样法等。比较成熟的统计分析方法包括回归分析法、ANOVA分析法、基于方差分解的方法、分类与回归树分析法。而图解法则是通过图表形式来表现敏感性，通常被用来形象化显示输入变化对输出结果的影响，也可用于表现复杂的输入输出关系，如散点图法。

筛选分析法通常用来初步识别敏感参数以减少参数维数，因其简单且应用方便，多用于参数众多的模型分析。一般认为其存在较大的不稳定性，结果可能受模型主要特征的影响较大，如非线性特征，相互作用性以及不同的参数类型。精炼方法则更适应于复杂模型特征的分析，因需要更多的资源来实现或解释，往往需要较大的计算量，相较于筛选法应用起来较为困难，但其给出的定量分析较筛选法的定性判断更精确。

3 水文模型参数敏感性分析方法

全局敏感性分析方法在水文模型中的应用日益增多，其可靠性也得到了广泛验证。一方面是考虑了各参数概率分布的影响，另一方面是计算分析时，所有参数都可同时变化。该类方法的主要优点是可将参数变动范围扩展到整个定义域，且不受模型构建的主观限制，能够对非线性和非单调模型进行分析［5，26，33］。在此选择水文模型参数敏感性分析的常用方法(筛选分析法，回归分析法，基于方差的分析方法以及代理模型法)，分析其各自的优缺点及适应条件，为今后的合理有效应用提供参考。

3.1 筛选分析方法

最常用的筛选分析方法是Morris筛选法，最初是由Morris［34］在1991年提出的，作为一种定性的全局敏感性分析方法被广泛应用，可用来筛选与识别最敏感的参数(组)。通常Morris筛选法采用两个计算指标:基效应的均值μ和标准差σ，用来判断参数的重要程度或敏感性。由于部分参数对基效应均值μ存在负效应，在一定程度上会导致评判结果存在偏差，因此，Campolongo等［35］采用修正的均值 μ*表示参数对输出结果的综合效应。均值表征参数的灵敏度从而确定参数的敏感性排序，而标准差表征参数之间相互作用的程度，标准差大说明该参数与其他参数的相互作用大，标准差小则说明该参数与其他参数的相互作用小。按照上述的分析，Morris筛选法的最大特点是应用起来相对简单，计算量不大，对于参数很多的复杂模型特别适合，通过少量的模型计算就可以获得模型参数的定性排序，从而识别出相对重要的参数以达到简化模型的目的。该方法虽然可能将不重要参数判断为重要参数，但不会出现将重要参数判为不重要参数的错误［36］，不足的是仅给出定性判断，而无法给出定量结果。Morris法在确定模型各参数灵敏度大小排序上相对简单有效，可用来冻结那些敏感性小的参数，选择敏感性相对大的参数进行定量的全局敏感性分析。

Morris筛选法在水文模型中的应用比较常见，如宋晓猛等［36-38］将其应用于分布式时变增益模型和新安江模型(日尺度和小时尺度)的参数敏感性分析，通过减少模型参数维数从而提高模型敏感性评价的效率，为模型参数进一步分析提供了极大的便利。Yang等［39］将其应用于中国潮白河流域和斯洛伐克Margecany流域的WetSpa模型的参数敏感性分析，以锁定不重要的参数，为SDP方法的进一步应用提供方便。Ruano等［40］同样也利用 Morris法筛选识别水质模型中的重要参数。除了上述的直接应用外，Griensven等［41-42］引入 LHS抽样方法，提出了LH-OAT法，并将其用于SWAT模型的一个应用中，此后该方法被广泛推广到SWAT模拟系统中，成为SWAT模型敏感性分析的主要工具，在多个流域得到验证和使用［43-44］;该方法也被用于其他水文模型的参数分析中，如AutoWEP模型［45］、流溪河模型［46］。

3.2 回归分析方法

回归分析方法是目前常用的敏感性分析方法之一，已建立了多种评价指标，如标准回归系数SRC(standardized regression coefficient)、偏相关系数PCC(partial correlation coefficient)，以及相应的秩变换SRRC(standardized rank regression coefficient)和PRCC(partial rank correlation coefficient)。一般而言，SRC和PCC适用于线性关系，而相应的秩变换指标则适用于非线性但单调的输入输出关系。若参数之间不相关，则SRC和PCC的结果是一致的，否则会存在较大的差异，两者的主要区别是PRC可消除相关性的影响而适用于存在相关关系的参数，SRC则仅适应于不相关的参数。

回归分析方法的优点在于能在所有输入同时影响输出的情况下，分析单项输入敏感性，同时能够描述输入输出间的关系，应用起来简单方便。该方法用于非线性关系或非单调关系时往往效果较差，虽说对部分非线性关系可以通过秩变换进行分析，但也存在不足，即无法有效分析非单调模型和无法将结果转换到原模型中［47］。Tiscareno-Lopez 等［48］利用回归分析方法分析WEPP水文模型的参数敏感性，指出参数估计的误差导致模型模拟的不确定性;He等［49］采用 Spearman's秩回归系数分析了SNOW17模型的参数敏感性，根据回归系数的显著性检验结果实现输入因素的敏感性排序;Muleta等［50］采用LHS抽样方法，利用逐步回归分析方法分析SWAT模型的参数敏感性;王浩昌等［51］将其用于分析典型城市降雨径流模型SWMM模型的水文参数的全局敏感度，识别模型中的敏感参数以减少后续参数率定的计算量。

3.3 基于方差分解的方法

基于方差分解的方法是指通过判定各个因素的方差贡献率来估计参数的重要程度的一种方法［52-53］，其基本理论是方差分解理论［5，33］。通常方差分解的方法采用一阶敏感度和总敏感度两个指标评价模型参数的敏感性，一阶敏感度主要考虑单一参数对输出结果的主要贡献，而总敏感度则考虑单个参数及其相应参数组合对输出结果的共同影响。一般总敏感度包括该参数的一阶敏感度以及其高阶敏感度，通过总敏感度与一阶敏感度的差值可以初步评判参数的交互作用影响［5，33，52-53］。

作为全局性分析方法，基于方差分解的Sobol方法、FAST方法和扩展FAST方法能够给出各因素的定量评判结果，除此之外，基于方差分解方法的优点还包括独立于模型之外，允许输入因素在整个取值区间变化，可考虑输入因素极端情况下对输出的影响，是应用比较广泛的一种方法。当输入因素较多时该方法计算量相对较大，应用较为复杂。任启伟等［27，54］采用 Sobol方法分析了 TOPMODEL 模型参数的敏感性问题，采用扩展FAST方法分析了新安江模型的参数敏感度，确定了在这些模型应用过程中，需要重点关注的模型参数;Werkhoven等［55］采用Sobol方法分析了SAC-SMA模型的参数敏感性，Wagener等［56］在此基础上提出了多目标函数条件下的SAC-SMA模型参数敏感性分析，能有效识别模型参数对不同目标响应的影响程度;Francos等［57］利用Morris方法和FAST方法计算评估SWAT模型的参数敏感性，两种方法的结合既有效地筛选出重要参数，又实现了参数的定量敏感性分析。

3.4 基于代理模型技术的方法

基于代理模型技术的方法是近年来发展起来的一种敏感性分析方法，其基本思路是通过一些统计方法和实验设计方法来近似估计输入参数与模型输出之间的函数响应关系，利用该函数响应关系近似代替原来的物理过程模型或概念模型，在此基础上结合一些定量分析方法估计参数变化对输出结果的影响程度，得出模型参数的敏感度指标。作为最常用的基于代理模型技术的方法，响应曲面法(response surface method，RSM)构建一个简单模型来替代初始模型，可得到输出与单个或多个输入之间的关系，在尽可能保证模型基本特征的同时降低了模型计算的时间消耗［25］，使快速模拟运算成为可能，当模型评价的模拟次数很多、计算消耗时间过长时可考虑该方法。对于水文模型而言，模拟流域较大时计算量通常较大，因此该方法也适用于水文模型的相关评价分析中(如不确定性评价，敏感性分析或参数估计)［5，33，37-38，58］。但应用该方法时需要进行模型多次拟合和校正，且运用响应曲面的有效域不能超出生成校正数据的输入范围，与原模型相比，大部分的分析仅包含少数重要参数，而其他参数在响应曲面中很难得到反映。

响应曲面模型技术在应用过程中的关键是选择合适的拟合方法和抽样设计方法［1-2］。拟合方法要求能够较好地反映实际的输入、输出之间的函数响应，即可认为其近似真实地反映两者之间的关系，如非参数响应曲面模型等。对于抽样设计方法的要求就是确保参数取样能够尽可能全方位地采样，涵盖参数范围内的取值，有效的采样方法有Monte Carlo法，Latin Hypercube法，Sobol准随机序列采样法等。在进行敏感性评价过程中，这些方法往往与一些统计方法进行结合应用，如 Sobol法、FAST法。Sathyanarayanamurthy等［59］结合 3 种 代 理模 型(Kriging模型、径向基神经网络模型和支持向量机模型)和基于方差的定量敏感性分析方法(Sobol法和FAST法)分析了复杂的工程模型的敏感性问题;Li等［60-61］利用正交多项式方法研制了一个随机抽样的HDMR(high-dimensional model representation)法，并结合ANOVA法评价模型的参数敏感性;Ratto等［62］将 SDP(state-dependent parameter)法和 Sobol法结合运用也取得了较好的效果;宋晓猛等［5，33，37-38］利用 PSUADE 集成了 Sobol法和响应曲面模型(支持向量机SVM，多元自适应回归样条MARS)用于水文模型的敏感性分析中，相较于传统的Sobol法极大地提高了模型评价效率。

4 水文模型参数敏感性分析框架

一般而言，水文模型参数敏感性分析主要包括以下几个环节［63］:①确定合适的参数及其取值范围;②选择适当的参数抽样方法;③生成模型评价样本;④运行模型程序;⑤构建模型参数敏感性分析数据集;⑥选择敏感性分析方法;⑦分析模型参数敏感性并输出评估结果。确定模型参数及其取值范围是敏感性分析的首要工作。众所周知，诸多水文模型参数缺少明确的物理意义，往往不能确定模型参数的取值范围，而模型参数的取值范围将直接影响到模型参数评价的结果［64］，可通过分析不同取值范围对结果的影响程度来判断参数的敏感性。

关于参数抽样方法的选择，一般不同的分析方法往往有相对应的参数抽样方法，如Morris分析法对应Morris one-at-time抽样法。抽样方法的选择需要考虑抽样的覆盖性和可靠性，研究结果显示准随机序列抽样和拉丁超立方抽样是较佳的选择［25，32，63］，被广泛地应用在敏感性分析中。

模拟计算是模型参数敏感性分析最核心的环节，也是最耗时的环节。针对目前模型的复杂性以及计算需求的不断增加，如何高效地完成模型计算吸引了越来越多的关注，如采用高性能计算机、开展并行计算以及简化模型计算等等。此外，如何选择合适有效的方法进行分析是模型研究的一个重要工作。一般认为参数敏感性分析的执行效率与参数个数有着密切的关系，通常参数个数越多，执行效率就会越低，因此首先需要采用一些手段来降低参数维数，为参数下一步分析提供基础。当参数个数较多时更适合采用筛选法，其次是回归分析法，最后才是方差分解方法。因此可以采用一些手段，降低参数维数，为参数下一步分析提供基础。最常用的参数敏感性分析框架方法就是在定量分析之前，采用一些定性分析或筛选方法来确定相对重要的参数或影响较大的因素(图1)。现在有些研究针对各种分析的优势，提出一些多方法的综合分析或多方法集成应用，如Morris方法与Variance-based方法的集成应用最为常见，Francos等［56］采用两步分析方法，即Morris法和FAST法的集成应用于SWAT模型的参数敏感性分析;Zan 等［36-38，63］集合 Morris法、响应曲面法和Sobol法用于分布式时变增益水文模型和新安江模型的参数敏感性分析。

如何有效地表达模型敏感性评价结果，以及给出合理可信的结果是敏感性分析的最终环节。目前模型敏感度表达主要有图形化表达以及数值分析结果，可根据不同的需求采用不同的表达方式。

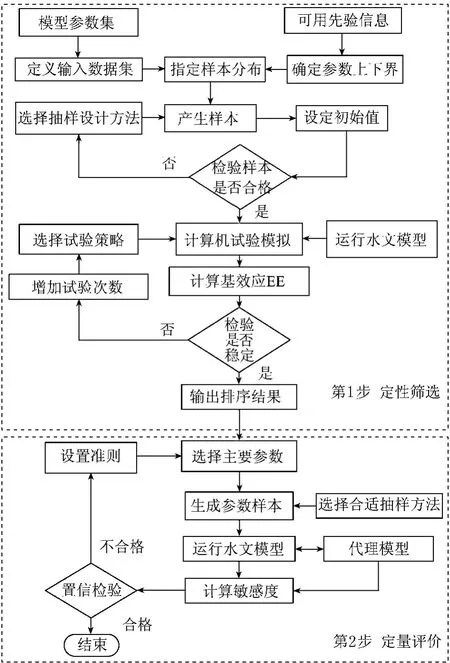
图1 集合算法流程

5 研究展望

水文模型参数敏感性分析为水文模型构建与应用的关键环节，其目的在于确定参数对模型结果的影响程度，从而剔除不重要的参数，减少参数维数，降低参数的不确定性影响，进而提高模型应用精度。参数敏感性分析方法众多，如何选择以及更高效地执行成为水文模型敏感性分析的关键。随着水文模型技术发展以及大尺度模型的应用需求，模型结构日益复杂，参数越来越多，敏感性分析越来越难。针对目前水文模型参数敏感性分析的不足，未来水文模型参数敏感性分析的研究方向主要有:

a．计算效率问题。对于复杂的模型而言，计算效率问题一直困扰着模型分析及优化，即成千上万次模型计算的巨大消耗成为模型敏感性分析的一个难题。在使用高性能计算机的同时，也出现了计算方法的组合优化，以提高模型敏感性分析的计算效率，如目前已开展的代理模型技术研究以及筛选法与定量评估的结合等，但其中仍存在一些问题迫切需要解决，如代理模型的适应性、可靠性以及准确度等问题。今后，这些新技术或方法或许将成为水文模型敏感性分析的一个热点。

b．可靠性问题。模型敏感性分析方法的可靠性一直以来也颇受关注，其很大程度上影响了模型敏感性分析的准确性。在今后的研究中，需要根据各种方法的适应条件及优劣，选择不同的敏感性分析方法进行验证，从而给出更可靠的敏感性分析结果。此外，多目标条件下的模型评价问题也是影响敏感性分析可靠性的关键。现有的诸多研究多针对单目标分析，可能导致无法全面地掌握模型参数的敏感性问题，对于水文过程模拟而言，不同评价目标从不同的方面反映模拟结果的好坏，为此为有效应对模型参数的多目标优化应开展多目标条件的参数敏感性分析。

c．参数的相关性问题。许多的敏感性分析方法的基本前提假设是模型输入参数之间是相互独立的，然而通常情况下水文模型参数之间存在很强的相关性。这些参数之间相互影响，共同作用，且具有很强的物理联系，在一定程度上可能降低分析结果的准确性。如我国开发的新安江模型，其参数相关性问题特别显著，不仅表现在各个层次内部，同时各层次间的联系和影响也较明显。目前，针对相关性参数的分析，尚未提出一套有效完整的理论分析方法，虽说也有部分尝试，但仍需要更多的工作以适应未来更复杂的模型参数敏感性分析。

［1］SONG Xiaomeng，ZHAN Chesheng，KONG Fanzhe，et al.Advances in the study of uncertainty quantification for large-scale hydrological modeling system［J］.Journal of Geographical Sciences，2011，21(5):801-819.

［2］宋晓猛，占车生，孔凡哲，等.大尺度水循环模拟系统不确定性研究进展［J］.地理学报，2011，66(3):396-406.(SONG Xiaomeng，ZHAN Chesheng，KONG Fanzhe，et al.A review on uncertainty analysisoflarge-scale hydrological cycle modeling system［J］.Acta Geographica Sinica，2011，66(3):396-406.(in Chinese))

［3］BECK M B.Water quality modeling:a review of the analysis of uncertainty［J］.Water Resources Research，1987，23(8):1393-1442.

［4］SALTELLI A，SCOTT E M，CHAN K，et al.Sensitivity analysis［M］.Chichester:John Wiley ＆ Sons，2000:13-15.

［5］孔凡哲，宋晓猛，占车生，等.水文模型参数敏感性快速定量评估的 RSMSobol方法［J］.地理学报，2011，66(9):1270-1280.(KONG Fanzhe，SONG Xiaomeng，ZHAN Chesheng，et al.An efficient quantitative sensitivity analysis approach for hydrological model parameters using rsmsobol method［J］.Acta Geographica Sinica，2011，66(9):1270-1280.(in Chinese))

［6］TONG C.Self-validated variance-based methods for sensitivity analysis of model outputs［J］.Reliability Engineering ＆ System Safety，2010，95(3):327-267.

［7］FREY H C，PATIL R.Identification and review of sensitivity analysis methods［J］.Risk Analysis，2002，22(3):553-377.

［8］IMAN R L，HELTON J C.An investigation of uncertainty and sensitivity analysis techniques for computer models［J］.Risk Analysis，1988(8):71-90.

［9］SONG Xiaomeng，KONG Fanzhe，ZHAN Chesheng，et al.Hybrid optimization rainfall-runoff simulation based on Xinanjiang model and artificial neural network［J］.Journal of Hydrologic Engineering，2012，17(9):1033-1041.

［10］YANG Jing.Convergence and uncertainty analyses in Monte-Carlo based sensitivity analysis［J］.Environmental Modelling and Software，2011，26(4):444-457.

［11］PAPPENBERGER F，BEVEN K J，RATTO M，et al.Multimethod global sensitivity analysis of flood inundation models［J］.Advances in Water Resources，2008，31(1):1-14.

［12］CONFALONIERI R，BELLOCCHI G，BREGAGLIO S，et al.Comparison of sensitivity analysis techniques:a case study with thericemodelWARM ［J］.Ecological Modelling，2010，221:1897-1906.

［13］CASTAINGS W，DARTUS D，LE DIMET F X，et al.Sensitivity analysis and parameter estimation for distributed hydrological modeling:potential of variational methods［J］.Hydrology and Earth System Science，2009，13:503-517.

［14］CIBIN R，SUDHEER K P，CHAUBEY I.Sensitivity and identifiability of stream flow generation parameters of the SWAT model［J］.Hydrological Processes，2010，24:1133-1148.

［15］刘毅，陈吉宁，杜鹏飞.环境模型参数识别与不确定性分析［J］.环境科学，2002，23(6):6-10.(LIU Yi，CHEN Jining，DU Pengfei.Parameter identification and uncertainty analysis in environmentalmodels［J］.EnvironmentalScience，2002，23(6):6-10.(in Chinese))

［16］ROSOLEM R，GUPTA H V，SHUTTLEWORTH W J，et al.A fully multiple-criteria implementation of the Sobol’method for parameter sensitivity analysis［J］.Journal of Geophysical Research，2012，117，D07103，doi:10.1029/2011JD016355.

［17］MISHRA S.Uncertainty and sensitivity analysis techniques for hydrologic modeling［J］.Journal of HydroInformatics，2009，11(3/4):282-296.

［18］王纲胜，夏军，陈军锋.模型多参数灵敏度与不确定性分析［J］.地理研究，2010，29(2):263-270.(WANG Gansheng，XIA Jun，CHEN Junfeng.A multi-parameter sensitivity and uncertainty analysis method to evaluate relative importance of parameters and model performance［J］.Geographical Research，2010，29(2):263-270.(in Chinese))

［19］BEVEN K，BINLEY A.The future of distributed models:modelcalibration and uncertainty predication［J］.Hydrological Processes，1992，6(3):279-298.

［20］SPEAR R C，HORNBERGER G M.Eutrophication in peel inlet-Ⅱ.Identification of critical uncertainties via generalized sensitivity analysis［J］.Water Research，1980，14(1):43-49.

［21］RATTO M，TARANTOLA S，SALTELLI A.Sensitivity analysis in model calibration:GSA-GLUE approach［J］.Computer Physics Communications，2001，136(3):212-224.

［22］ELSAWWAF M，WILLEMS P，FEYEN J.Assessment of the sensitivity and prediction uncertainty of evaporation models applied to Nasser Lake，Egypt［J］.Journal of Hydrology，2010，395(1/2):10-22.

［23］van WERKHOVEN K，WAGENER T，REED P，et al.Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models［J］.Advances in Water Resources，2009，32(8):1154-1169.

［24］LIU Yang，SUN Fan.Sensitivity analysis and automatic calibration of a rainfall-runoff model using multi-objectives［J］.Ecological Informatics，2010，5(4):304-310.

［25］SALTELLI A，RATTO M，ANDRES T，et al.Global sensitivity analysis，the primer［M］.Chichester:John Wiley ＆ Sons，2008，18-20.

［26］徐崇刚，胡远满，常禹，等.生态模型的灵敏度分析［J］.应用 生 态 学 报，2004，15(6):1056-1062.(XU Chonggang，HU Yuanman，CHANG Yu，et al.Sensitivity analysis in ecological modeling［J］.Chinese Journal of AppliedEcology，2004，15(6):1056-1062.(in Chinese))

［27］任启伟，陈洋波，舒晓娟.基于Extend FAST方法的新安江模型参数全局敏感性分析［J］.中山大学学报:自然科学版，2010，49(3):127-134.(REN Qiwei，CHEN Yangbo，SHU Xiaojuan.Global sensitivity analysis of Xinanjiang model parameters based on extend FAST method［J］.Acta Scientiarum Naturalium Universitatis Sunyatseni，2010，49(3):127-134.(in Chinese))

［28］BRUN R，REICHERTP，KUNSCH H R.Practical identifiability analysis of large environmental simulation models［J］.Water Resources Research，2001，37(4):1015-1030.

［29］WOTAWA G，STOHL A，KROMPKOLB H.Estimating the uncertainty of a lagrangian photochemical air quality simulation model caused by inexact meteorological input data［J］.Reliability Engineering ＆ System Safety，1997，57(1):31-40.

［30］MOKHTARI A，FREYHC.Recommendedpractice regarding selection of sensitivity analysis methods applied to microbial food safety process risk models［J］.Human and Ecological Risk Assessment，2005，11(3):591-605.

［31］CANNON A J，MCKENDRY I G.A graphical sensitivity analysis for statistical climate models:application to Indian monsoon rainfall prediction by artificial neural networks and multiple linear regression models［J］.International Journal of Climatology，2002，22(13):1687-1708.

［32］宋晓猛，占车生，夏军，等.流域水文模型参数不确定性量化理论方法与应用［M］.北京:中国水利水电出版社，2014.

［33］ SONG Xiaomeng，ZHAN Chesheng，XIA Jun，et al.An efficient global sensitivity analysis approach for distributed hydrological model［J］.Journal of Geographical Sciences，2012，22(2):209-222.

［34］MORRIS M D.Factorial sampling plans for preliminary computational experiments［J］.Technometrics，1991，33(2):161-174.

［35］CAMPOLONGOF，CARIBONIJ，SALTELLIA.An effective screening design for sensitivity analysis of large models［J］.Environmental Modelling and Software，2007，22(10):1509-1518.

［36］ZHAN Chesheng，SONG Xiaomeng，XIA Jun，et al.An efficient integrated approach for global sensitivity analysis of hydrological model parameters［J］.Environmental Modelling and Software，2013，41:39-52.

［37］宋晓猛，孔凡哲，占车生，等.基于统计理论方法的水文模型参数敏感性分析［J］.水科学进展，2012，23(5):642-649.(SONG Xiaomeng，KONG Fanzhe，ZHAN Chesheng，et al.Sensitivity analysis of hydrological model parameters using statistical theory［J］.Advances in Water Science，2012，23(5):642-649.(in Chinese))

［38］SONG Xiaomeng，KONG Fanzhe，ZHAN Chesheng，et al.Parameter identification and global sensitivity analysis of Xinanjiang model using meta-modeling approach［J］.Water Science ＆ Engineering，2013，6(1):1-17.

［39］YANG Jing，LIU Yangbo，YANG Wanhong，et al.Multiobjective sensitivity analysis ofa fully distributed hydrologic model WetSpa ［J］.Water Resources Management，2012，26:109-128.

［40］RUANO M V，RIBES J，FERRER J，et al.Application of the Morris method for screening the influential parameters of fuzzy controllers applied to wastewater treatment plants［J］.Water Science ＆ Technology，2011，63(10):2199-2206.

［41］van GRIENSVEN A，MEIXNER T，GRUNWALD S，et al.A global sensitivity analysis tool for the parameters of multi-variable catchment models［J］. Journal of Hydrology，2006，324(1/2/3/4):10-23.

［42］HOLVOET K，van GRIENSVEN A，SEUNTJENS P et al.Sensitivity analysis for hydrology and pesticide supply towards the river in SWAT［J］.Physics and Chemistry of the Earth:Parts A/B/C，2005，30(8/9/10):518-526.

［43］NOSSENT J，BAUWENS W.Multi-variable sensitivity and identifiability analysis for a complex environmental model in view of integrated water quantity and water quality modeling［J］.Water Science ＆ Technology，2012，65(3):539-549.

［44］SINGH A，IMTIYAZ M，ISAAC R K，et al.Comparison of soil and water assessment tool and multilayer perceptron(MLP)artificial neural network for predicting sediment yield in the Nagwa agricultural watershed in Jharhand，India［J］.Agricultural Water Management，2012，104:113-120.

［45］LEI Xiaohui，TIAN Yu，LIAO Weihong，et al.Development of an AutoWEP distributed hydrological model and its application to the upstream catchmentofthe Miyun Reservoir［J］.Computers ＆ Geosciences，2012，44:203-213.

［46］徐会军，陈洋波，李昼阳，等.基于LH-OAT分布式水文模型参数敏感性分析［J］.人民长江，2012，43(7):19-23.(XU Huijun，CHEN Yangbo，LI Zhouyang，et al.Parameter sensitivity analysis of distributed hydrological model based on LH-OAT［J］.Yangtze River，2012，43(7):19-23.(in Chinese))

［47］SALTELLI A，SOBOL’IM.Abouttheuseofrank transformation in sensitivity analysis of model output［J］.Reliability Engineering ＆ System Safety，1995，50(3):225-239.

［48］TISCARENO-LOPEZ M，LOPES V L，STONE J J，et al.Sensitivity analysis of the WEPP watershed model for rangeland applications I:Hillslope processes［J］.Transactions of The ASAE，1993，36(6):1659-1672.

［49］HEMinxue，HOGUE T S，FRANZ K J，etal.Characterizing parameter sensitivity and uncertainty for a snow model across hydroclimatic regimes［J］.Advances in Water Resources，2011，34(1):114-127.

［50］MULETA M K，NICKLOW JW.Sensitivityand uncertainty analysis coupled with automatic calibration for a distributed watershed model［J］.Journal of Hydrology，2005，306(1/2/3/4):127-145.

［51］王浩昌，杜鹏飞，赵冬泉，等.城市降雨径流模型参数全局灵敏度分析［J］.中国环境科学，2008，28(8):725-729.(WANG Haochang，DU Pengfei，ZHAO Dongquan，et al.Global sensitivity analysis for urban rainfall-runoff model［J］.China Environmental Science，2008，28(8):725-729.(in Chinese))

［52］SALTELLI A，TARANTOLA S，CHAN K.A quantitative model-independent method for global sensitivity analysis of model output［J］.Technometrics，1999，41(1):39-56.

［53］SOBOL’I M. Sensitivity estimates for nonlinear mathematical models［J］.Math Model Comput Exp，1993，14(4):407-414.

［54］任启伟，陈 洋 波，周 浩 澜，等.基 于 Sobol法 的TOPMODEL模型全局敏感性分析［J］.人民长江，2010，41(19):91-94.(REN Qiwei，CHEN Yangbo，ZHOU Haolan，etal.Globalsensitivity analysisof TOPMODEL parameter based on Sobol method［J］.Yangtze River，2010，41(19):91-94.(in Chinese))

［55］van WERKHOVEN K，WAGENER T，REED P，et al.Characterization of watershed model behavior across a hydroclimatic gradient［J］.Water Resources Research，2008，44，W01429，doi:10.1029/2007WR006271.

［56］WAGENER T，van WERKHOVEN K，REED P，et al.Multiobjective sensitivity analysis to understand the information content in streamflow observations for distributed watershed modeling［J］.Water Resources Research， 2009， 45， W02501， doi:10.1029/2008WR007347.

［57］FRANCOS A，ELORZA F J，BOURAOUI F，et al.Sensitivity analysis of distributed environmental simulation models:understanding the model behavior in hydrological studies at the catchment scale［J］.Reliability Engineering＆ System Safety，2003，79(2):205-218.

［58］宋晓猛，占车生，夏军.集成统计仿真技术和SCE-UA方法的水文模型参数优化［J］.科学通报，2012，57(26):2530-2536.(SONG Xiaomeng，ZHAN Chesheng，XIA Jun.Integration of a statistical emulator approach with the SCE-UA method for parameter optimization of a hydrological model［J］.Chinese Science Bulletin，2012，57(26):2530-2536.(in Chinese))

［59］SATHYANARAYANAMURTHYH，CHINNAMRB.Metamodels for variable importance decomposition with applications to probabilistic engineering design［J］.Computers ＆ Industrial Engineering，2009，57(3):996-1007.

［60］LIGenyuan， ROSENTHAL C， RABITZ H.High dimensional model representation［J］.The Journal of Physical Chemistry，2001，105(33):7765-7777.

［61］LI Genyuan，WANG Shengwei，RABITZ H，et al.Global uncertainty assessments by high dimensionalmodel representations(HDRM)［J］.Chemical Engineering Science，2002，57(21):4445-4460.

［62］RATTO M，PAGANO A，YOUNG P.State dependent parameter metamodelling and sensitivity analysis［J］.Computer Physics Communications，2007，177(11):863-876.

［63］宋晓猛.基于响应曲面方法的分布式时变增益水文模型不确定性量化研究［D］.徐州:中国矿业大学，2012.

［64］SHIN M J，GUILLAUME J H A，CROKE B F W，et al.Addressing ten questions about conceptual rainfall-runoff models with global sensitivity analysis in R［J］.Journal of Hydrology，2013，503:135-152.