蒙山天池堆石自密实混凝土拱坝三维有限元分析

2015-12-16郁章文

水利建设与管理 2015年8期

郁章文刘刚

(山东省临沂市水利勘测设计院，山东临沂 276000)

1 引言

蒙山天池堆石自密实混凝土拱坝坝体采用单曲拱坝，最大坝高24.0m，坝顶外弧半径为50m，最大中心角为78°。坝长130m，其中中间拱坝段68m，左端重力墩28.46m(包括拱座)，右端重力墩33.54m(包括拱座)，分别与两岸连接。坝顶高程815.00m，拱坝坝顶宽度为4.0m，最大坝底宽为10.0m。坝体断面上游面为铅直面，下游面为折坡，上部3m为直线段，下部坡比为1∶0.33。坝顶设4孔溢流堰，总净宽20m，堰顶高程814.00m。详见图1、图2。

蒙山天池工程筑坝材料采用堆石自密实混凝土。堆石混凝土是在自密实混凝土技术基础上发展起来的一种新型大体积混凝土施工技术，已获得国家专利。堆石混凝土施工首先将满足一定粒径要求的堆石直接入仓，形成有空隙的堆石体，然后在堆石体表面浇筑满足特定要求的自密实混凝土，利用其特有的高流动、抗离析、强填充黏结性能，依靠自重完全充填堆石体空隙，形成完整、密实、有较高强度和低水化热的大体积混凝土。自密实混凝土是指在浇筑过程中无需施加任何振捣，仅依靠混凝土自重就能完全填充至模板内任何角落和钢筋间隙的混凝土。

图1 蒙山天池平面布置

图2 蒙山天池溢流段剖面

根据蒙山天池拱坝的工程特点，利用大型软件ANSYS，建立拱坝的三维非线性有限元分析模型，仿真模拟拱坝的运行性态，研究拱坝在运行期的应力变形特性，分析评价拱坝结构设计的合理性和安全性，并相应优化调整拱坝设计，满足工程需求。

2 计算理论

ANSYS程序提供一种以Drucker-Prager为屈服准则的材料，该材料选项适用于混凝土、岩石土壤等颗粒状材料。

Drucker-Prager准则实际是对Mohr-Coulomb准则的修正。由于Mohr-Coulomb准则在π平面上的屈服轨迹为六角形，它在主应力空间的屈服面有一个奇异的顶点，为消除角点，Drucker和Prager对其提出修正，他们建议用一个正圆锥面来代替上述的不规则六角锥面。在π平面上的屈服轨迹为一圆。其屈服函数表示为

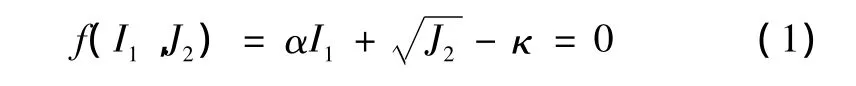
式中 I1、J2——分别为应力张量的第一不变量和应力偏张量的第二不变量;

α、κ——为材料常数，它们与内摩擦角 φ和黏聚力c的关系为

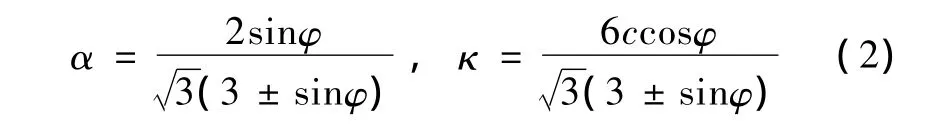
其中，“+”号对应于 Drucker-Prager圆锥面与Mohr锥体的内角点相接，“-”号则对应于 Drucker-Prager圆锥面与Mohr锥体外接。若取α=0，则其退化为Mises准则－κ=0。

反映材料本构关系的弹塑性矩阵Dep为Dep=D(1－r)DP(3)

式中 D、Dp——分别为弹性与塑性本构阵;

A——为材料硬化参数。

由于ANSYS采用的Drucker-Prager屈服面为Mohr-Coulomb屈服面的外接圆锥，式(2)取“-”。屈服面不随材料的逐渐屈服而改变，即没有强化准则，但屈服强度随侧限压力的增加而相应增加，塑性行为假定为理想弹塑性。采用相关联流动法则，即流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的。考虑由于屈服而引起的体积膨胀，但不考虑温度变化的影响。另外，塑性应变的大小与加载速度无关。

对DP材料，其受压时的屈服强度大于受拉时的屈服强度。如果有材料的单轴受拉屈服应力和单轴受压屈服应力，可以通过下式将此二值转换为程序所需的输入值

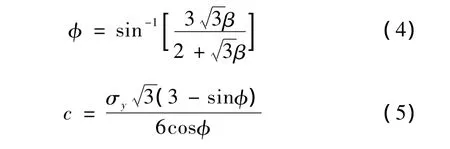
式中 β和σy可由受压屈服应力和受拉屈服应力计算出

3 计算模型

3.1 网格生成

根据有限元设计规范及参考相关类似工程，利用有限单元法计算拱坝应力时，单元的剖分应尽量达到设计所要求的精度，单元形式结合拱坝体型合理选用。计算坐标系规定为:X轴为坝轴线向(横河向)，由左岸指向右岸;Y轴为顺河向，指向下游;Z轴为垂直向，竖直向上，与高程一致。

根据蒙山天池拱坝的坝体结构及坝基岩体的资料(包括断面、地质剖面等)，结合类似工程经验，截取有限元模型计算范围如下:横河向截取长度总计为200m，左岸截取至左岸坝肩以外44.0m，右岸截取至右岸坝肩以外42.0m;顺河向截取长度总计为100m，上游截取至坝踵以外31.5m，下游截取至坝趾以外58.5m;铅直向上边界按地形实际高度模拟，底部边界截取至坝基面以下41m;三个方向截取范围均为1～2倍坝高。此外，该三维有限元整体模型忽略了放水洞等附属结构的影响。

有限元模型划分网格时，遵循尽量模拟坝体的实际形态的原则，使之反映坝体的实际情况。模型离散后，单元结点总数为14479个，单元总数为12135个，蒙山天池拱坝三维有限元网格如图3所示。拱坝坝体沿高度方向自动剖分为12层，沿厚度方向剖分为4层，拱坝坝体有限元网格如图4所示。

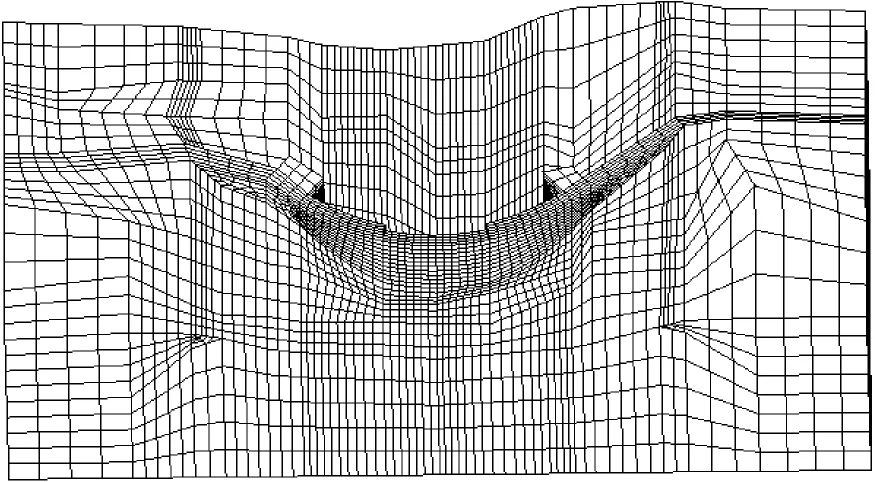
图3 蒙山天池拱坝三维有限元网格

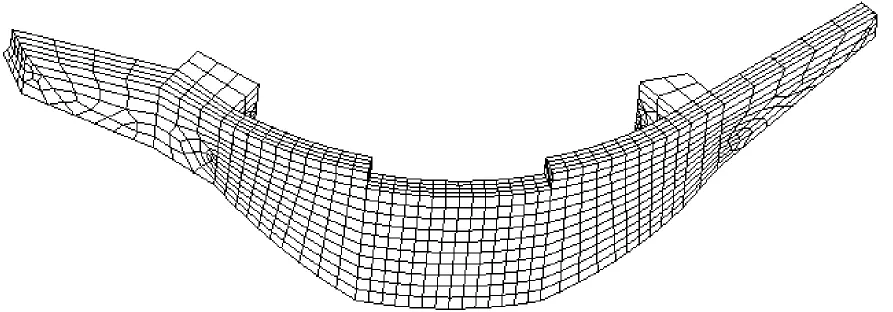
图4 蒙山天池拱坝坝体有限元网格

3.2 计算参数

温度应力分析时，利用ANSYS热分析模块，采用solid70单元模拟拱坝坝体和坝基岩体;应力场分析时，利用ANSYS静力分析模块，采用solid45单元模拟坝基岩体，采用solid65单元模拟混凝土单元。

根据蒙山天池拱坝坝体设计资料以及坝基岩体勘测资料，拱坝及重力墩等坝体材料采用堆石混凝土，坝基材料主要为中风化花岗岩，各材料的具体计算参数如表1所列。

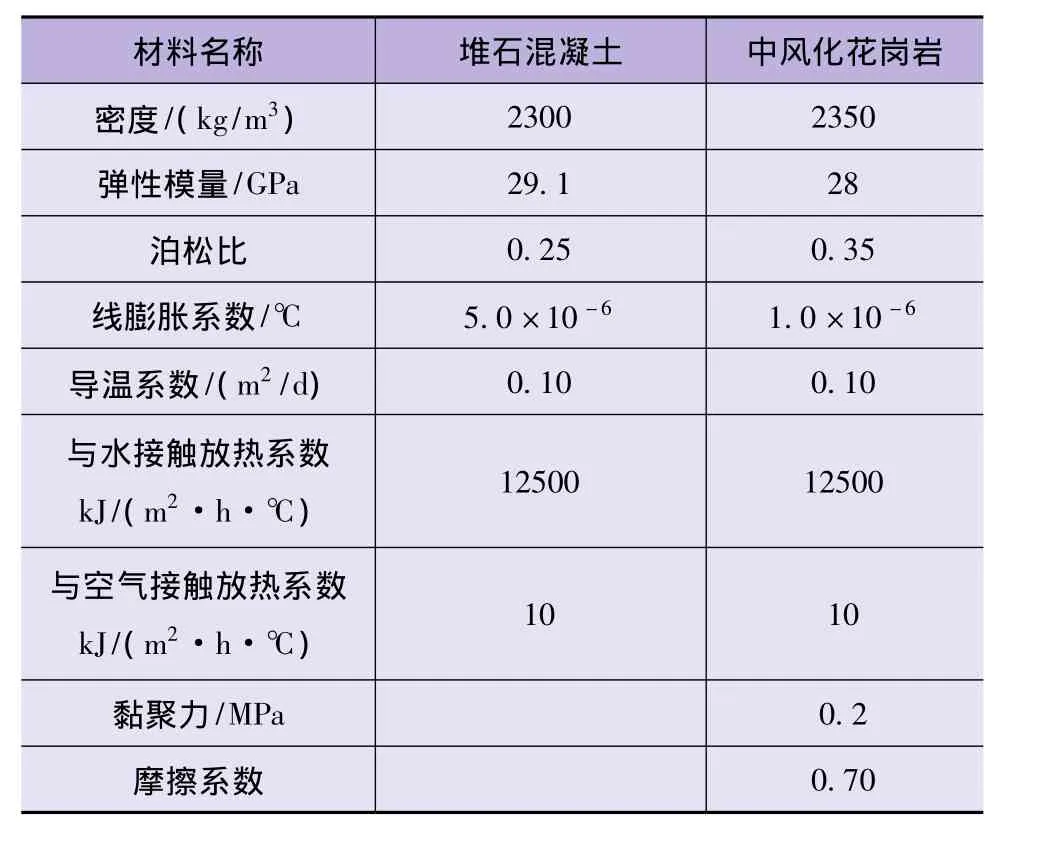
表1 材料参数

3.3 计算工况

根据《混凝土拱坝设计规范》(SL 282—2003)中的相关规定，本次分析考虑了自重、上下游静水压力、温度荷载和扬压力等不同组合。坝体自重不考虑分期施工的影响。

混凝土拱坝设计荷载组合分为基本荷载组合和特殊荷载组合两类。基本组合由基本荷载组成，特殊组合除相应的基本荷载外，还应包括某些特殊荷载。

3.3.1 基本组合

工况1:正常蓄水位+正常温降+自重+扬压力;

工况2:设计洪水位+正常温升+自重+扬压力;

工况3:死水位+正常温降+自重+扬压力;

工况4:死水位+正常温升+自重+扬压力。

3.3.2 特殊组合

工况5:校核洪水位+正常温升+自重+扬压力。

3.4 计算成果

根据已建立的三维有限元分析模型、计算参数和荷载组合工况，利用有限元分析软件ANSYS，分别计算蒙山天池拱坝基本组合工况和特殊组合工况下的位移和应力分布。

基本组合工况和特殊组合工况下的各工况计算得到的特征位移如表2所示，特征应力见表3。

表2 各工况中坝体最大位移统计单位:mm

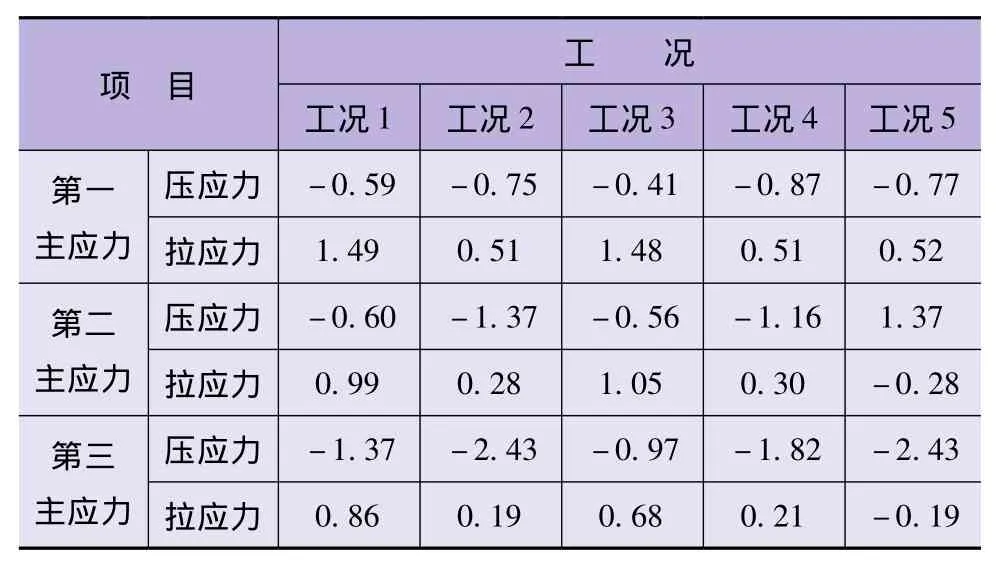
表3 各工况中坝体最大应力统计

3.5 成果分析

3.5.1 位移分析

从各计算工况的位移可知，坝体的顺河向、横河向、竖直向三个方向的位移均表现出关于拱冠梁断面的对称性。从表2可知:工况1、工况2和工况3坝体向下游向发生径向位移，最大位移发生在坝顶溢流坝段处;工况1(正常水位+温降)和工况3(死水位+温降)由于上游水压力和温降荷载的共同作用，顺河向位移分别为6.39mm和2.91mm;工况2(设计洪水位+温升)和工况5(校核洪水位+温升)，坝体受高水位静水压力的影响，其水平位移基本偏向下游但由于受温升温度场的影响，偏向下游量有所减少，最大值为5.94mm和5.77mm，处于拱冠梁顶部、拱端和拱座的局部附近区域，由于受温升温度荷载的影响，坝体水平位移偏向上游，最大值分别为0.36mm和0.37mm，处于坝体拱端。在工况4(死水位+温升)下，由于水压力荷载较小，受温升作用影响明显，坝体向上游向径向位移较大，其值达10.44mm，主要是由于拱坝温升荷载较大，而且坝体单薄受温度荷载影响明显。

在各工况下，通过综合比较坝体与坝基的位移，坝体的各位移变化量要比坝基位移大，其中坝体沉降量最大值为9.15mm，均小于最大坝高的1%，坝体水平位移和沿坝轴线向位移均在mm数量级左右，因此该坝体位移符合拱坝位移的一般规律。

3.5.2 应力分析

本次计算中只考虑温度场变化对应力场的影响，忽略坝体应力变化对温度场的影响。从各计算工况的位移可知，拱坝坝体应力也表现出关于拱冠梁断面的对称性。通过对各荷载组合情况下大坝三维有限元的应力计算，可知坝体上游面的压应力一般来说都是随着水位的升高而增大，上游面的拉应力也随着水位的升高而增大。通过对各荷载组合情况下大坝三维有限元的应力计算，可知坝体上游面的压应力一般来说都是随着水位的升高而增大，上游面的拉应力也随着水位的升高而增大。坝体第三主应力基本为压应力，仅有局部区域出现拉应力，根据温度场的变化，拉应力位置也有所不同，但其分布范围较小。

在各工况下，通过综合比较坝体应力分布图和表3，坝体在工况2(设计洪水位+温升)和工况5(校核洪水位 +温升)的最大压应力值分别为2.43MPa和2.43MPa，小于混凝土抗压强度4.5MPa。工况1(正常蓄水位+温降)和工况3(死水位+温降)下，坝体局部拉应力区较大，最大值分别为1.49MPa和1.48MPa，其值小于抗拉要求值1.5MPa，并且在坝体拉应力较大部位铺设钢筋后，坝体抗拉强度进一步提高，同时由于坝基面应力计算时存在应力集中问题，实际应力应小于计算值，因此，从应力角度来看，坝体可满足抗拉强度和抗压强度要求。