基于因子分析的城市隧道出口运行车速模型

余 婷，马健霄，耿孝健

(南京林业大学汽车与交通工程学院，南京210037)

近年来，随着城市快速发展，隧道建设占城市基础建设比重越来越大［1］。由于隧道只在出入口处需用极少用地，因此可以节约用地;隧道内基本车道的车辆行车条件较好，其行车速度比一般城市地面道路要快，接近于高架道路或快速路，车辆能够保持畅通持续行驶［2-3］。城市隧道不仅可以完善路网结构，缩短城区之间的距离，有效实现城市交通分流，而且提高了城市土地利用率，促进了城市的规划与建设，但隧道出入口的安全问题也是交通工程领域研究热点和难点。隧道进出口是形成事故黑点的主要路段，同时，车辆拥堵，通行能力差也是城市隧道的常见问题，在隧道出入口处尤为明显［4］。车辆行驶速度是影响隧道交通安全、保证通行能力的关键因素，因此，对隧道出入口运行速度进行研究具有重要的现实意义。

国内外对隧道的研究成果有很多。外国学者关于隧道方面的研究较倾向于隧道内部的安全以及驾驶人生理、心理变化方面的研究。国内关于隧道出入口方面的研究大多是基于高速公路隧道出入口，对城市隧道出入口研究较少。对隧道开展的研究工作主要集中在行车速度、线形安全设计、安全评价［5］等方面。

在隧道车速研究方面，国内的赵忠杰等对隧道速度有影响的所有因素归结为交通状况、环境状况和交通需求3类，给出了最佳速度模糊逻辑算法［6］;杨轸等利用自主开发的三轴加速度仪研究了隧道进出入口的车速变化规律，并得到了隧道进出入口的加速度均值［7］;王琰等基于隧道进出入口实测车速以及车速差指标之间的关系对线形进行安全评价［8］;杜志刚等利用眼动仪及三轴加速度仪研究了隧道进出入口驾驶员的瞳孔变化与行车速度之间的关系，提出了驾驶员的临界安全行车速度85km/h［9］;祝站东等用统计回归方法建立了隧道路段小客车运行车速模型［10］。杜立平分析了影响隧道口驾驶员行车速度的三个主要因素［11］:隧道洞内外光线差值、路基宽度差值及洞口位置，运用Origin软件统计得出高速公路隧道入口运行车速计算模型。阎莹等通过对隧道进出入口车辆运行速度变化特征及线形过渡的分析，构建反映平纵组合特征的隧道进出入口线形综合描述模型［12］。

本文基于因子分析法，从城市隧道出入口交通特性着手，构建城市隧道出口的车速模型，对隧道安全研究与评价具有重要意义。

1 城市隧道出口运行车速影响因素

城市隧道出口交通特性主要包括驾驶人特性、汽车动力性能、隧道出口线形、环境特性等4个方面，但是限于人的因素和车辆因素难以量化，本文主要调查了南京主城区的玄武湖隧道，九华山隧道和富贵山隧道出口处的道路条件和环境条件，影响因素见表1。

表1 影响因素表Tab．1 Influence factors

其中，在道路方面，不同的道路等级，对车辆的运行速度要求不同，道路通行能力也不同。道路等级的不同间接地反映出不同隧道交通量、车辆速度、车型比例、车头时距等问题的差异性。为减小变量因子间的相关性，不影响方程迭代结果的稳定性，故舍去道路等级这一因素;《公路隧道设计规范》(JTJ D70-2004)规定［13］，在城市隧道中，纵坡坡度不应小于0．3%，且不应大于3%，受地形等条件限制时，高速公路的中、短隧道(L≦1 000 m)可适当加大，但不宜大于4%。一般情况下，城市隧道出入口坡度变化范围较小。据统计研究，小型车动力性能较好，在上下坡过程中，受纵坡影响较小。同时，长安大学王亚群在运行速度的相关研究中指出随着纵坡的增加，与速度并不呈现一定的规律，相关小［14］。故本文建模时暂且不考虑纵坡对速度的影响。

在交通运行环境方面，路面在干湿状态和不同速度下的摩擦系数变化如图1所示［15］。隧道出入口车速一般在20～60km/h范围内，由图1可知，路面摩擦系数的较小变化，故可以忽略路面摩擦系数对车速的影响。

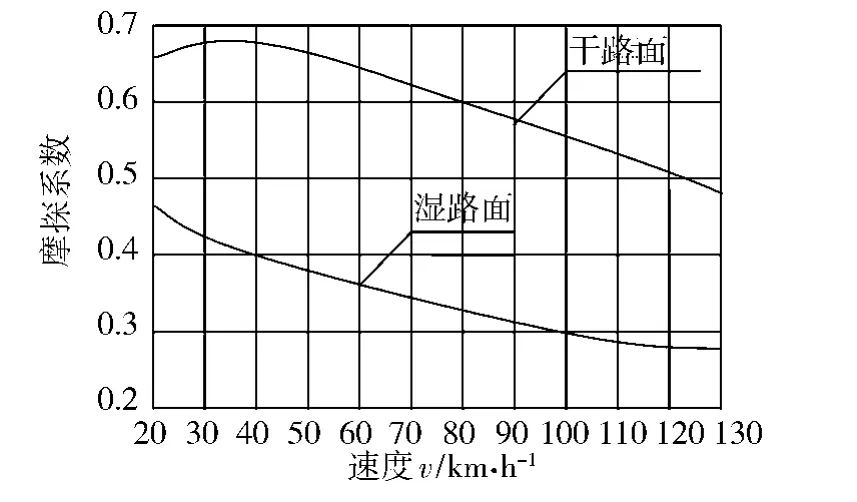
图1 摩擦系数变化图Fig．1 The changes of friction coefficients

综上所述，本文将影响隧道出口车速的主要因素归纳为:大车比率、平均车头时距、洞内外亮度差值、交通量、单洞宽度这几个因素。

2 运行车速因子分析

车辆处于自由行驶状态时，驾驶员感知到与前车的速度差较大，前后车辆速度差无明显关系。当车头时距较小时，前车对后车的影响较大，车辆处于跟驰状态;城市隧道占地面积有限，车辆间影响比较明显。研究隧道高峰期的车速特性更有研究价值，因此，选取玄武湖，九华山，富贵山隧道17∶00～18∶00的交通与环境数据。大车比率、车头时距、洞内外亮度差值和交通量等为实时动态变化的数据，为简化分析，故取平均值。将数据导入到SPSS数据窗口中，先定义各变量为数值型，将各数值标准化，后选择降维因子分析，设置相关功能，得到结果如图2～图7所示。

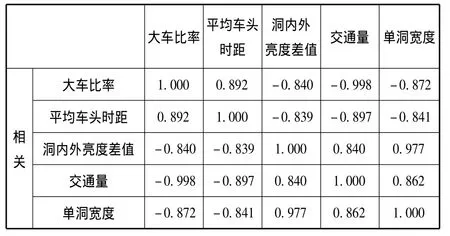
图2 相关矩阵Fig．2 Correlation matrix

图3 KMO和Bartlett的检验Fig．3 KMO and Bartlett's test

KMO检验是检验数据是否符合因子分析，KMO检验值取值范围为0～1。其中，0．9～1表示非常合适，0．8～0．9表示合适，0．7～0．8表示一般，0．6～0．7表示不太合适，0．5～0．6表示糟糕，0．5以下表示不可接受。此次检验结果为0．700，表示一般，即可进行因子分析。Bartlett检验中Sig．值为0．000，小于显著性水平0．05，表示数据来自正态分布的总体，可以进行下一步分析。

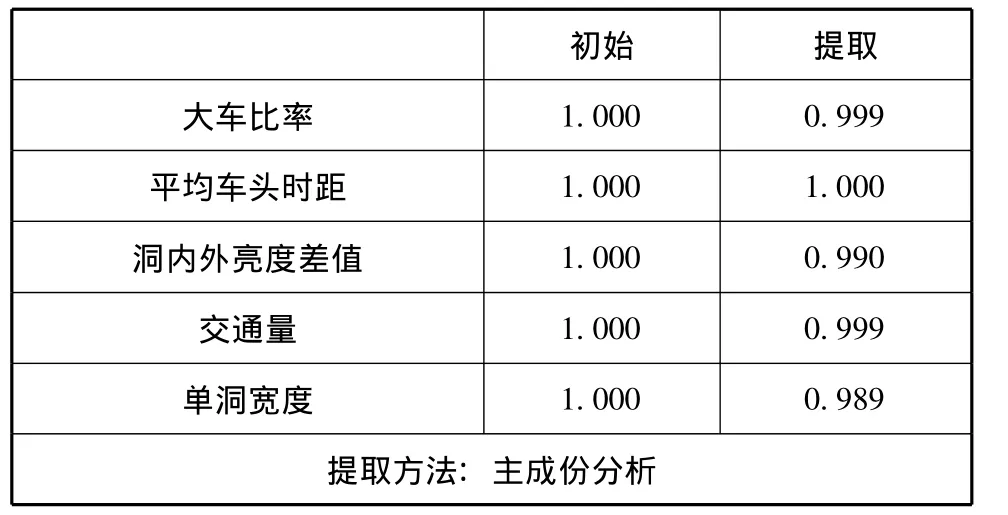
图4 公因子Fig．4 Factor variance

公因子方差也可以称变量共同度，表示提取的公因子能解释各个变量中所含原始信息的程度。在上图中，所有公因子方差都在95%以上，故被提取的公因子解释能力较强，能较好地概括原变量的信息。

图5 解释的总方差Fig．5 The total variance

图6 成分矩阵Fig．6 Component matrix

没有经过旋转的载荷矩阵中，因子变量在许多变量上都有较高的载荷。因子含义较模糊。经过旋转后，因子含义略加清楚。旋转后成分矩阵如下:

图7 旋转成分矩阵Fig．7 Rotating component matrix

变量与某一因子的联系系数绝对值越大，则该因子与变量关系越近。如本例洞内外亮度差值与第一因子的值为 0．843，与第二因子的值为 0．400，与第三因子的值为0．347，表示其与第一因子关系更近，与第二、三因子较远。因此，因子矩阵也可以作为因子贡献大小的指标，其绝对值越大，贡献也越大。故第一个因子主要反映了洞内外亮度差值，而第二个因子主要反映了大车比率，第三因子主要反映平均车头时距的信息。

根据以上SPSS软件的分析，影响城市隧道出入口运行车速的主要因素应当为大车比率，平均车头时距，洞内外亮度差值。由此，自变量缩小为这3个变量。

3 运行车速回归模型

利用SPSS进行多元线性回归，从而建立车速模型。打开SPSS界面，将数据录入，设因变量为y(运行车速)，自变量(影响因素)为x1(大车比率)、x2(平均车头时距)、x3(洞内外亮度差值)，见表2。

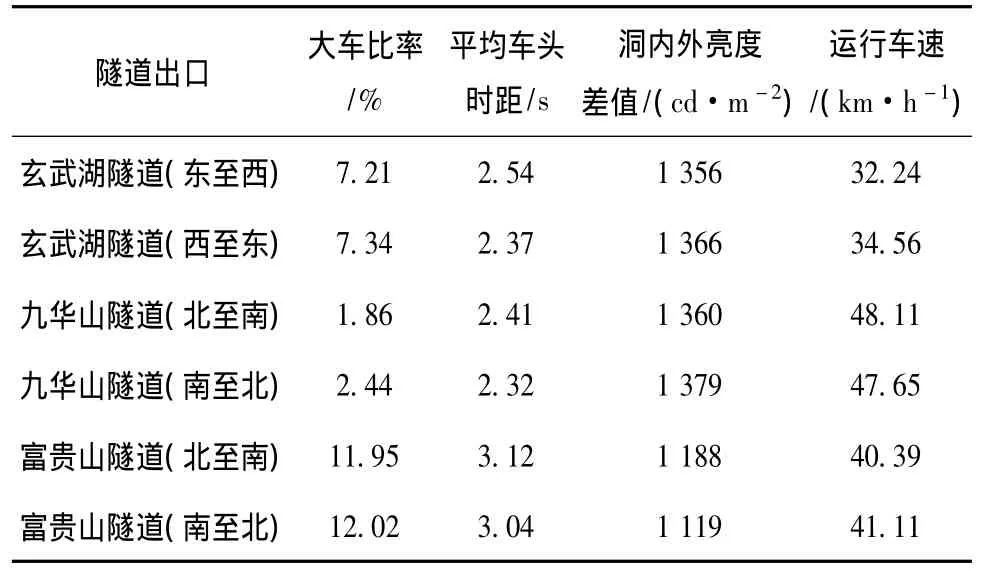
表2 自变量数据表Tab．2 Independent variable data

经过软件的回归分析得到下列结果，如图8～10。

图8 模型汇总Fig．8 The model summary

该图输出的是常用统计量。R为复相关系数，表示模型中自变量与因变量之间线形回归关系的密切程度，取值为0～1。R越大，则线形回归关系越密切。调整R2值越大，模型拟合效果越好。标准估计误差S越小，建立模型的效果越好。从这部分结果看出相关系数 R=0．942，判定系数 R2=0．720，调整的判定系数 R2=0．896，回归估计的标准误差S=2．104 22。说明样本回归效果较好。

图9 离散分析Fig．9 Discrete analysis

上表显示，Sig．=0．003＜0．005 表示该模型显著，多个自变量与因变量之间存在线性回归关系。

图10 回归方程系数Fig．10 The regression coefficients

图10可知，自变量的概率P值都小于显著性水平0．05，符合回归要求。从表格中可以得到城市隧道出口处车速与影响因素之间的相关性回归模型:

式中:y为运行车速，km/h;x1为大车比率，%;x2为平均车头时距，s;x3为洞内外光线差值，cd/m2。

公式(1)就是城市隧道出口处车速模型，从模型中可以看出，隧道洞内外亮度差值和大车比率会降低隧道洞口的运行车速，这与实际情况较为符合。

4 模型验证

4．1 实例基础资料

西安门隧道位于龙蟠中路瑞金路交织段至军区西大门交织段，隧道全长1．84 km，双向6车道，车道宽度3．5 m，隧道净高4．5 m，设计车速60 km/h，道路类型属于快速路，隧道限速60 km/h。龙蟠中路是南京市“井”字形快速内环的重要组成部分，北接九华山隧道，南连赛虹桥立交，是市内车辆快速进出主城及城东南北向车流运行的主通道，建成以后车流量增长较快，早晚高峰经常发生拥堵。验证所需数据选取西安门隧道下午5点至6点的实测数据，具体数值见表3。

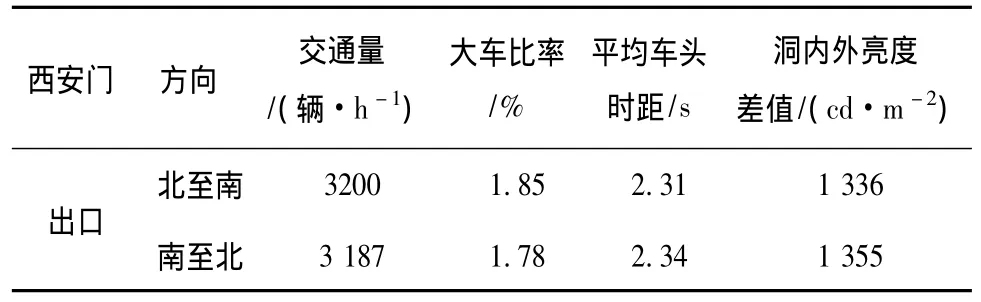
表3 南京西安门隧道调查数据Tab．3 Survey data of Nanjing Xi'an gate tunnel

4．2 运行车速预测与校验

西安门隧道(北至南)出口方向:

y=127．148-2．813x1+8．262x2-0．068x3

=127．148-2．813 × 1．85+8．262 × 2．31-0．068 ×1 336=50．18。

西安门隧道(南至北)出口方向:

y=127．148-2．813x1+6．262x2-0．068x3

=127．148-2．813 × 1．78+8．262 × 2．34-0．068 ×1 355=49．34。

将速度计算数据和实际数据进行比较，见表4。

表4 隧道出口运行车速实际测量值和计算值的比较Tab．4 The comparison of the actual measured value and calculated value of driving speed

可以看出，用模型计算出来的运行车速与实际测量出的运行车速相差较小，误差均控制在了5%左右，预测效果较为优异。

5 结论

本文主旨在于通过对实测数据的整理、分析，得到了城市隧道出口的运行车速模型。主要成果如下:

(1)对南京主城区主要隧道交通状况基本调研，分析并建立车速模型。对南京主城区主要隧道出入口进行实地勘察、数据采集得到了建立模型所必须的基础资料，再利用SPSS软件对数据进行分析、回归得出隧道出入口车速模型。

(2)应用实例验证模型。通过已建立的车速模型，应用实例对南京主城区西安门隧道出入口进行车速预测，通过与实测数据的对比，进一步检验模型。本文还存在一些不足之处，本文的速度模型未考虑驾驶人和车辆自身的影响，可以进一步考虑驾驶人及车辆自身对速度的影响，可测量不同驾龄的驾驶人通过隧道出入口时脑电、心电、皮肤电等数值，以及车辆自身动力性能与线形统筹考虑隧道运行速度。

［1］杨 轸，郭忠印．隧道进出口车速变化研究［J］．上海公路，2006(1):48-51．

［2］童林旭．中国城市地下空问的发展道路［J］．地下空间与工程学报，2005，2(1):1-6．

［3］王 敏．城市发展对地下空间的需求研究［D］．上海:同济大学，2006．

［4］ Amundsen F H，Ranes G．Studies on traffic accidents in Norwegian road tunnels［J］．Tunnelling and Underground Space Technology，2000，15(1):3-11．

［5］戴忧华，郭忠印，马 艳，等．高速公路隧道运行环境安全评价指标研究［J］．同济大学学报(自然科学版)，2010，38(8):1171-1176．

［6］赵忠杰，田 梅，董敏娥，等．公路隧道内最佳行驶速度模糊算法［J］．长安大学学报:自然科学版，2007，27(3):67-70．

［7］杨 轸，郭忠印．隧道进出口车速变化研究［J］．上海公路，2006(1):48-51．

［8］王 琰，孔令旗，郭忠印，等．基于运行安全的公路隧道进出口线形设计［J］．公路交通科技，2008，25(3):134．

［9］杜志刚，潘晓东．高速公路隧道进出口视觉震荡与行车安全研究［J］．中国公路学报，2007，20(5):101-105．

［10］祝站东，荣 建，周 伟．高速公路隧道路段小客车运行速度模型研究［J］．公路交通科技，2010，27(7):123-127．

［11］杜立平，刘润有，高立鑫．基于Origin的隧道入口运行车速计算模型探析［J］．交通标准化，2010(Z1):34-36．

［12］阎 莹，张宇辉，郭忠印．基于运行速度的隧道进出口线形安全性评价［J］．长安大学学报:自然科学版，2010，30(4):72-76．

［13］中华人民共和国交通部．JTJ D70-2004公路隧道设计规范［S］．北京:人民交通出版社，2004．

［14］王亚群．高速公路隧道小客车运行速度预测模型研究［D］．西安:长安大学，2010．

［15］王少飞，陈建忠，涂 耘．公路隧道的交通特点研究［J］．道路交通与安全，2009，9(1):36-40．