基于松弛序列法的温室传感器优化布置研究

贾鹤鸣，宋文龙

(东北林业大学机电工程学院，哈尔滨150040)

解决系统传感器的优化布置问题，首先要根据目标的不同确定优化准则，然后选择适当的优化方法［1，2］。常用的配置的优化方法分为传统方法和随机类算法两类。随机类算法如模拟退火［3］、遗传算法［4］等;传统方法中基于MAC法提出的序列法最为实用，设计的基本思想是每次从剩余的候选布放位置中选择最优的一个加入现有解，直至目标函数达到设定条件。

松弛思想源于图论中的最短路径问题。该问题中，将路径长度的估计值类比为弹性绳子的长度。最初，路径的长度被高估，就像一根拉长的弹性绳子。当较短的路径出现时，估计值随之下降，就像弹性绳子被松弛了一样。同样的，如果最短路径被找到，就相当于弹性绳子被完全放松［5］。

随着环境问题对人类生活和生产的影响日益加剧，森林资源的保护和发展越来越重要。幼苗抚育是林业发展的基础，幼苗抚育质量直接关系到未来林木的质量和林地的生产力［6-7］。因此，对温室林木幼苗抚育的研究具有很强的现实意义，如何将先进的自动化技术应用于温室育苗中也就成为了重要的研究课题［8-10］。为获得良好的幼苗抚育效果，高效、环保地对温室中的传感器数量和位置进行优化就显得十分重要。本文在序列法的基础上，通过融入松弛思想，提出基于松弛序列法的温室传感器优化配置方法。松弛序列法首先执行积累序列法得到不同传感器个数对应的初始布置方案，然后对每个初始布置方案进行松弛操作，使其求解的结果得到进一步优化。

1 基于松弛序列法的传感器优化布置

1．1 基础理论

n个自由度系统的方程可以表示为:

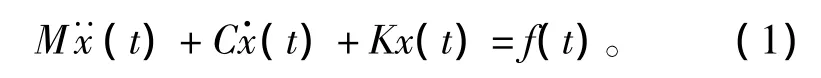
式中:M、C、K、f(t)和x(t)分别表示质量矩阵、阻尼矩阵、刚度矩阵、力向量和响应向量。依据模态叠加性原理，响应向量可以表示为:

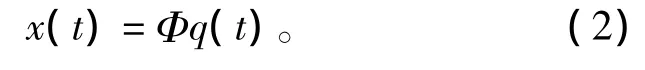
式中:Φ为模态振型矩阵;q(t)为模态坐标向量。

实际工程应用中，工程师需要观察模态振型，即通过视觉来判断模态的精度。

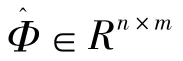
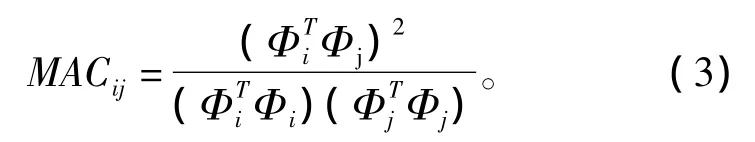
式中:Φi和Φi分别为Φ的第i列和第j列;Φ为布放方案的振型矩阵。

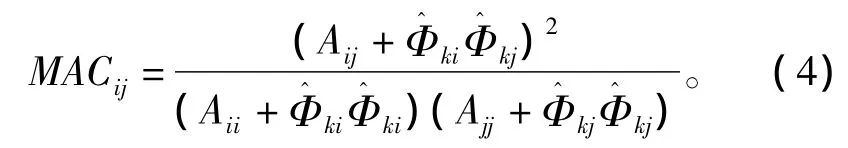
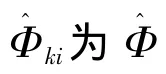
公式(4)表明，在现有布置方案基础上添加一个传感器的计算量较小。同理，去除一个传感器的计算量也较小。

1．2 积累序列法

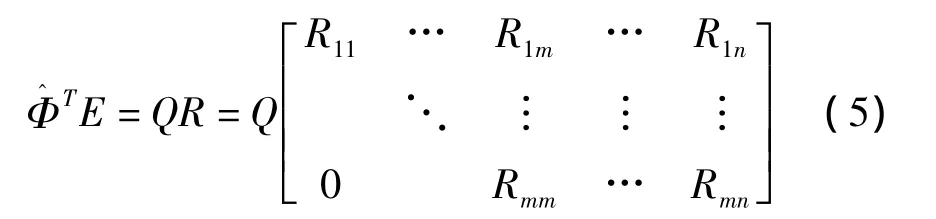
通过QR分解求出含有m个传感器的布置方案，将剩余的未布放位置分别加入初始解中，并分别计算对应的公式(3)所述函数值，从中选取最优的一个布放位置，放置传感器，形成含有m+1个传感器的布置方案。同样的方式，可以得到含有m+2，m+3，…个传感器的布置方案。

1．3 松弛思想

松弛思想是在原有估计的基础上，通过增广现有解，得到新解，当增广解优于现有的解时，原有估计将被更新。通常对于组合优化问题，贪心策略只能找到次优解，目标函数的估计值被高估，即初始解的张力较大，可以采用合理的松弛操作释放张力，降低目标函数的估计值，获取更优的解。

合理地选择松弛操作是成功应用松弛思想的关键，传感器优化布置的松弛序列法采用以最优方式增加和减小布放传感器的方式，执行松弛操作。

1．4 松弛序列法

松弛序列法将松弛思想引入传感器优化布置的积累序列法中，其执行过程通过以下步骤完成:

(1)根据1．2节描述的积累序列法，得到初始布置方案集合(布置方案集合的组成为含有m，m+1，…个传感器的布置方案)。

(2)遍历当前布置方案集合，执行松弛操作。例如:对于含有t个传感器的布置方案，选择使公式(3)所述函数值最优的布放位置，计算其增加一个传感器及减小一个传感器后产生的两个新布置方案(得到含有t-1个传感器的新布置方案和含有t+1个传感器的新布置方案)，如果新布置方案优于对应传感器个数的原有布置方案，则用新布置方案替换原有布置方案(松弛成功)，否则，保留原有布置方案(松弛失败)。

(3)如果步骤(2)中产生了松弛过程(即其中的某个解被松弛成功)，返回步骤(2)继续执行;反之，结束计算，输出结果。

传感器优化布置的松弛序列算法的流程如图1所示。

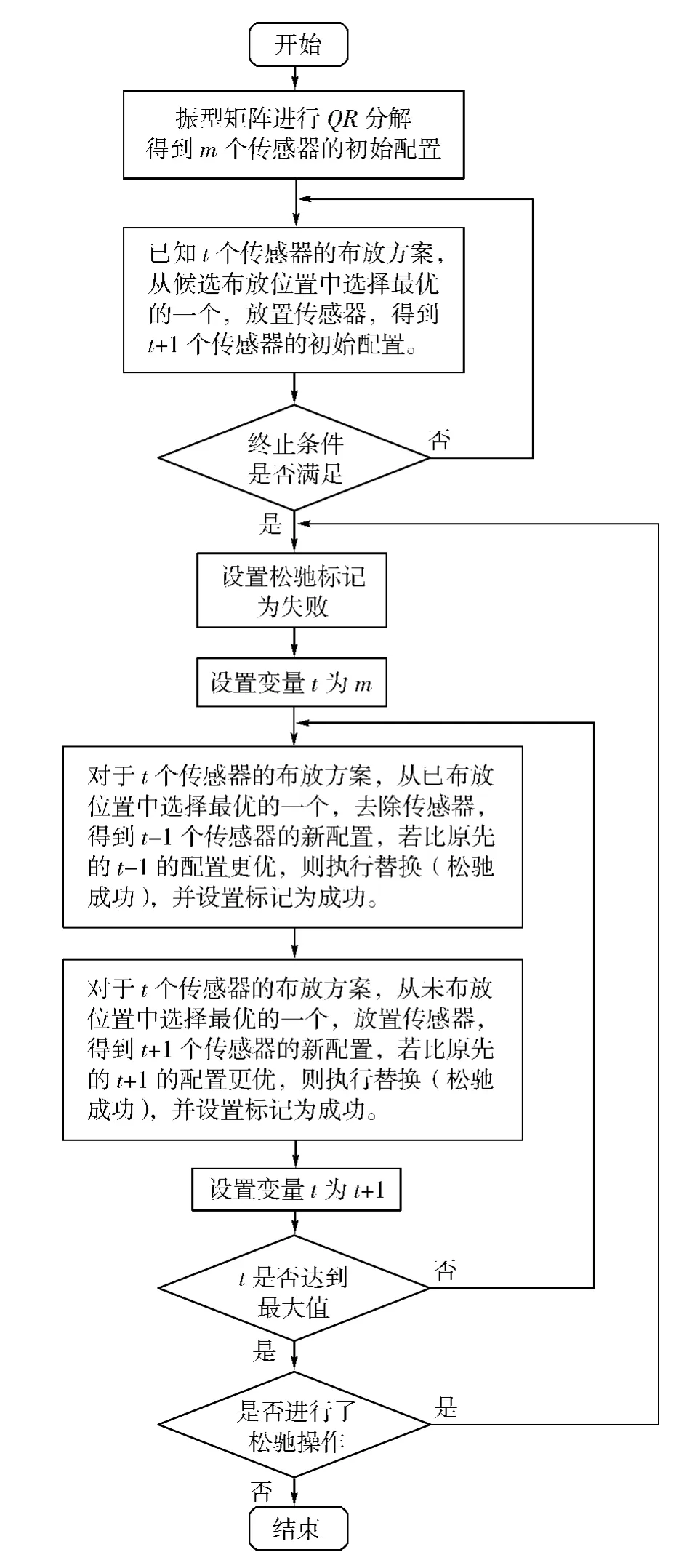
图1 算法实现流程图Fig．1 Flow chart of the algorithm

2 温室传感器优化配置仿真

以图2所示的林木幼苗抚育温室的气体传感器优化配置为例，实施传感器优化配置问题的松弛序列法仿真验证。待测植株位于同化实验箱内，同化箱采用透明材质，可以有效接受阳光;同化箱连接混合气体通道，并设有出气通道;同化箱内装有光照传感器、温度传感器、湿度传感器、气体浓度检测传感器，所有检测信号通过线缆通道进入控制单元(下位机)，控制单元将检测的数据信号输入计算机(上位机)，进行信号处理和显示。以MATLAB R2014b为仿真平台，基于计算流体力学软件进行分析，根据松弛序列法步骤编程，得出不同传感器个数下对应的布置方案。

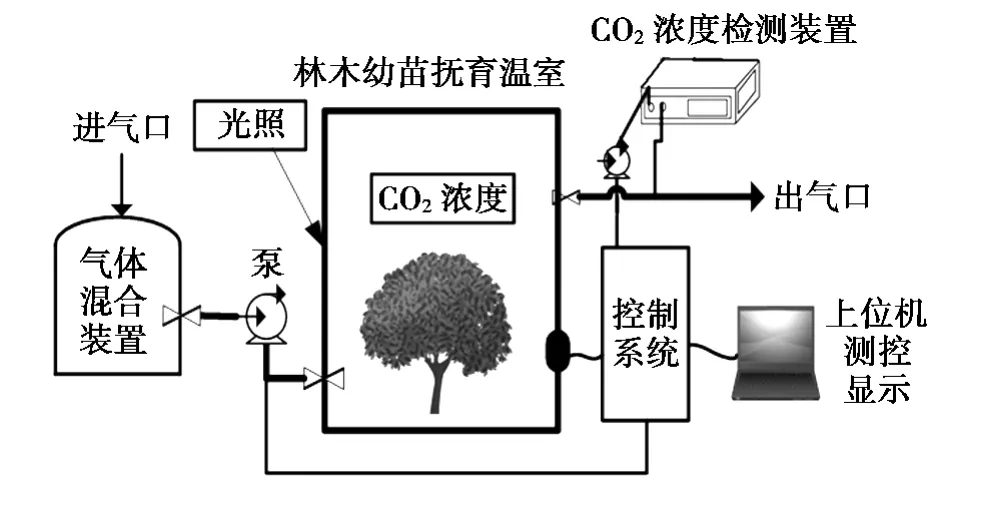
图2 林木幼苗抚育温室实验系统Fig．2 Seedling tending in greenhouse experiment system

为了验证松弛算法的布置效果，分别采用积累序列法和松弛序列法两种方法进行优化配置，配置结果如图3所示。图中显示被选气体浓度传感器个数分别为4～20个，两种算法的MAC矩阵最大非对角元素的大小。从图3中曲线可以看出，松弛序列法的布置效果明显优于积累序列法的布置效果。当目标函数取值相同时，松弛序列法和积累序列法的布置结果对比见表1，表明在模态相似性要求相同时，松弛序列法需要的传感器个数较少，有效减小了工程实验成本。

从图3中松弛序列法的曲线可以看出，当选择的传感器个数为10时，MAC矩阵最大非对角元素就已经达到很好的优化效果，继续增加传感器时曲线下降缓慢。因此本文最终选择10个传感器，作为温室气体传感器优化试验的最终配置。

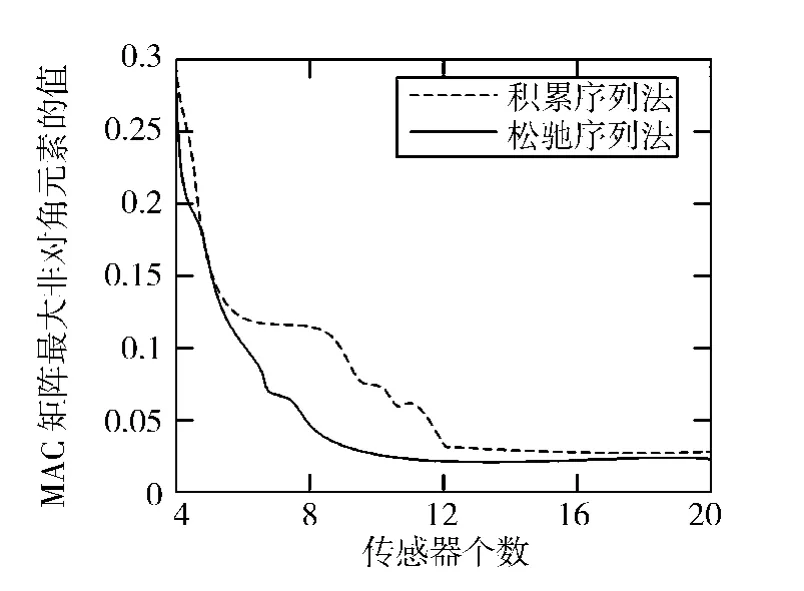
图3 两种算法的对比结果图Fig．3 Comparison results of the two algorithms

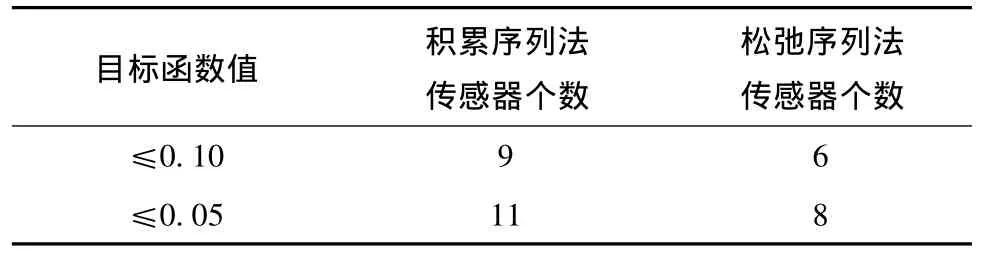
表1 相同目标函数取值时两种方法的布置对比结果Tab．1 Comparison results of the two methods with the same objective function value

3 结束语

将松弛思想应用于林木幼苗抚育温室传感器优化布置问题中，松弛序列法在积累序列法的基础上，使MAC矩阵的最大非对角元素进一步降低。当目标相似性的标准一致时，与积累序列法相比松弛序列法需要的传感器数目更少，不仅可以节约试验的成本，而且能够减少数据采集、数据传输和数据分析的工作量，大大提高温室幼苗的培育质量和培育效率。

［1］覃柏英，林贤坤，张令弥，等．基于整数编码遗传算法的传感器优化配置研究［J］．振动工程学报，2011，30(2):252-257．

［2］李 月，马海涛，林红波，等．基于核函数主成分的维纳滤波方法研究［J］．地球物理学报，2010，53(5):1226-1233．

［3］田 莉，陈换过，祝 俊，等．基于自适应模拟退火遗传算法的传感器优化配置研究［J］．振动工程学报，2012，25(3):238-243．

［4］耿 飞，龙海辉，赵健康，等．基于改进遗传算法的传感器优化配置［J］．计算机仿真，2014，31(5):56-59．

［5］ Cormen T H，Leiserson C E，Rivest R L，et al．Introduction to algorithms(Third Edition)［M］．Cambridge，Massachusetts:MIT press，2009．

［6］潘志明．生态林业建设中育苗技术的应用探析［J］．现代园艺，2014(10):65-66．

［7］杨 柳．森林种苗培育建设存在的问题及措施［J］．黑龙江科技信息，2014(9):253．

［8］李小婉，燕 飞，邰清清，等．基于GPRS技术的林木种苗抚育温室远程监控系统［J］．湖南农业科学，2010(21):159-161．

［9］李永博，周 伟，汪小旵，等．基于奇异摄动理论的综合温室控制系统设计［J］．农业机械学报，2012，43(5):184-189．

［10］王林生，王风燕，刘志刚，等．林木温室育苗机械自动化作业平台设计研究［J］．农机化研究，2014(12):107-110．