回归和时间序列的组合模型在建筑物变形监测数据处理中的应用

成　枢， 孙　超， 沈　毅， 李　强

(山东科技大学测绘科学与工程学院， 山东青岛 266590)



回归和时间序列的组合模型在建筑物变形监测数据处理中的应用

成枢， 孙超， 沈毅， 李强

(山东科技大学测绘科学与工程学院， 山东青岛 266590)

摘要：为了提高变形预测的精度，获得可靠有效的预报模型，通过对回归模型残差项的进一步分析，利用Eviews对残差序列建立了时间序列模型，从而得到了回归和时间序列组合模型.利用该模型对一组实测数据进行分析、预测，并将变形数据和实测数据进行比较，证明了组合模型具有更好的预测精度和可靠性.

关键词：回归分析； 时间序列； 组合模型

回归分析和时间序列分析是常用的变形监测数据处理方法[1]，这两种方法各有其优缺点.回归分析法在分析多因素模型时，更加简单和方便，也可以准确地计量各个因素之间的相关程度与回归拟合程度的高低.但有时在回归分析中，选用何种因子和该因子采用何种表达式只是一种推测，这影响了用到因子的多样性和某些因子的不可测性，使得回归分析在某些情况下受到限制.时间序列分析在分析现在、过去、未来的联系时，以及未来的结果与过去、现在的各种因素之间的关系时，效果比较好；但并不适合进行长期预测[2].如果把回归模型和时间序列模型这两种分析方法结合在一起，有时会得到比其中任何一种方法都好的预测结果.

1　回归与时间序列组合模型

1.1 一阶序列相关

如果线性回归方程的扰动项ut满足古典回归假设，使用OLS所得到的估计量是线性无偏最优的.

但是如果扰动项ut不满足古典回归假设，理论和实践均证明，扰动项关于ut关于任何一条古典回归假设的违背，都将导致回归方程的估计结果不再具有良好的性质.即对于不同的样本点，随机扰动项之间不再是完全相互独立的.而是存在某种相关性，则认为出现了序列相关性.特别的，如果仅存在

E(ut.ut-1)≠0t=1,2,…，T

(1)

称为一阶序列相关[3].

如果回归方程的扰动项存在序列相关，那么应用最小二乘法得到的参数估计量的方差将被高估或者低估.因此，检验参数显著性水平的t统计量将不再可信.

1.2组合模型

有如下回归模型 :

yt=β0+β1xt+ut

(2)

其中xt是解释变量，yt是被解释变量，ut是随机误差项.上述模型的估计式是:

(3)

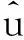
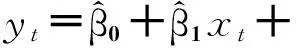
(4)

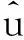
1.3残差序列的相关性检验

1) D.W.统计量检验

D.W.统计量用于检验一阶序列相关，还可以估计回归模型邻近残差的线性联系.对于扰动项ut建立一阶自回归方程[5]：

ut=ρut-1+εt

(5)

D.W.统计量检验的原假设：ρ=0,备择假设是ρ≠0[6].

(6)

如果序列不相关，D.W.值在2附近.如果序列正序列相关，D.W.值将小于2.如果存在负序列相关，D.W.值将在2∶4之间.

2)相关图和Q-统计量

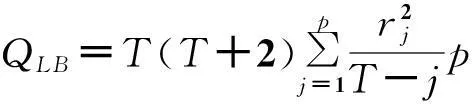
(7)

其中：rj是残差序列的j阶自相关系数，T是观测值的个数，p是设定的滞后阶数.

如果Q-统计量在某一滞后阶数显著不为零，则说明序列存在某种程度上的序列相关[7].在实际的检验中，通常会计算出不同滞后阶数的Q-统计量、自相关系数和偏自相关系数.如果，各阶Q-统计量都没有超过由设定的显著性水平决定的临界值，则接受原假设，即不存在序列相关，并且此时，各阶的自相关和偏自相关系数都接近于0.

3)LM检验

LM检验原假设为：直到p阶滞后不存在序列相关，p为预先定义好的整数；备择假设是：存在p自相关.检验统计量由如下辅助回归计算.

估计回归方程，并求出残差et[8]：

(8)

检验统计量可以基于如下回归得到

et=Xtγ+α1et-1+…+αpet-p+vt

(9)

这是对原始回归因子Xt和直到p阶的滞后残差的回归.LM检验通常给出两个统计量：F统计量和T×R2统计量.

在给定的显著性水平下，如果这两个统计量小于设定显著性水平下的临界值，说明序列在设定的显著性水平下不存在序列相关；反之，如果这两个统计量大于设定显著性水平下的临界值，则说明序列存在序列相关.

2　算例分析

某小区建筑物受临近基坑开挖深度(顶管一共30根，每根长3m)、开挖时间(2014年3月4日到2014年3月17日)、以及天气变化(有的时候天气变化)等因素的影响，本文选择了沉降量最大的 2号楼监测点J101点的25期数据，并对前20期观测数据采用回归与时间序列组合进行分析建模，后5期用来检验预测值的准确性(表1).

表1 沉降监测点J101数据

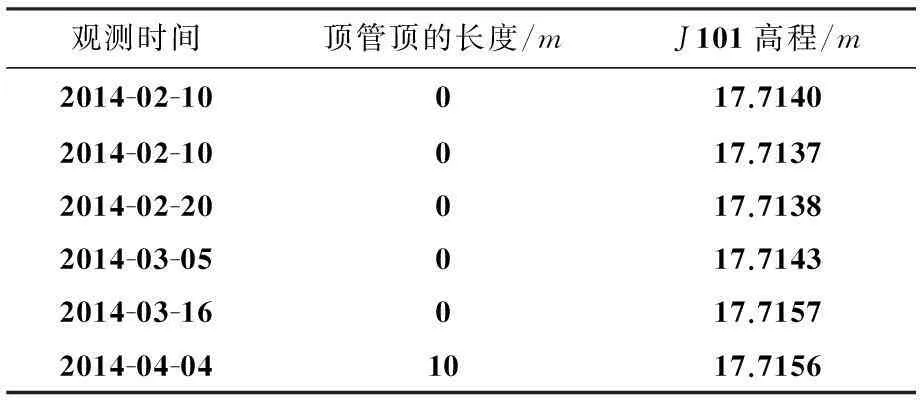
观测时间顶管顶的长度/mJ101高程/m2014-02-10017.71402014-02-10017.71372014-02-20017.71382014-03-05017.71432014-03-16017.71572014-04-041017.7156

续表

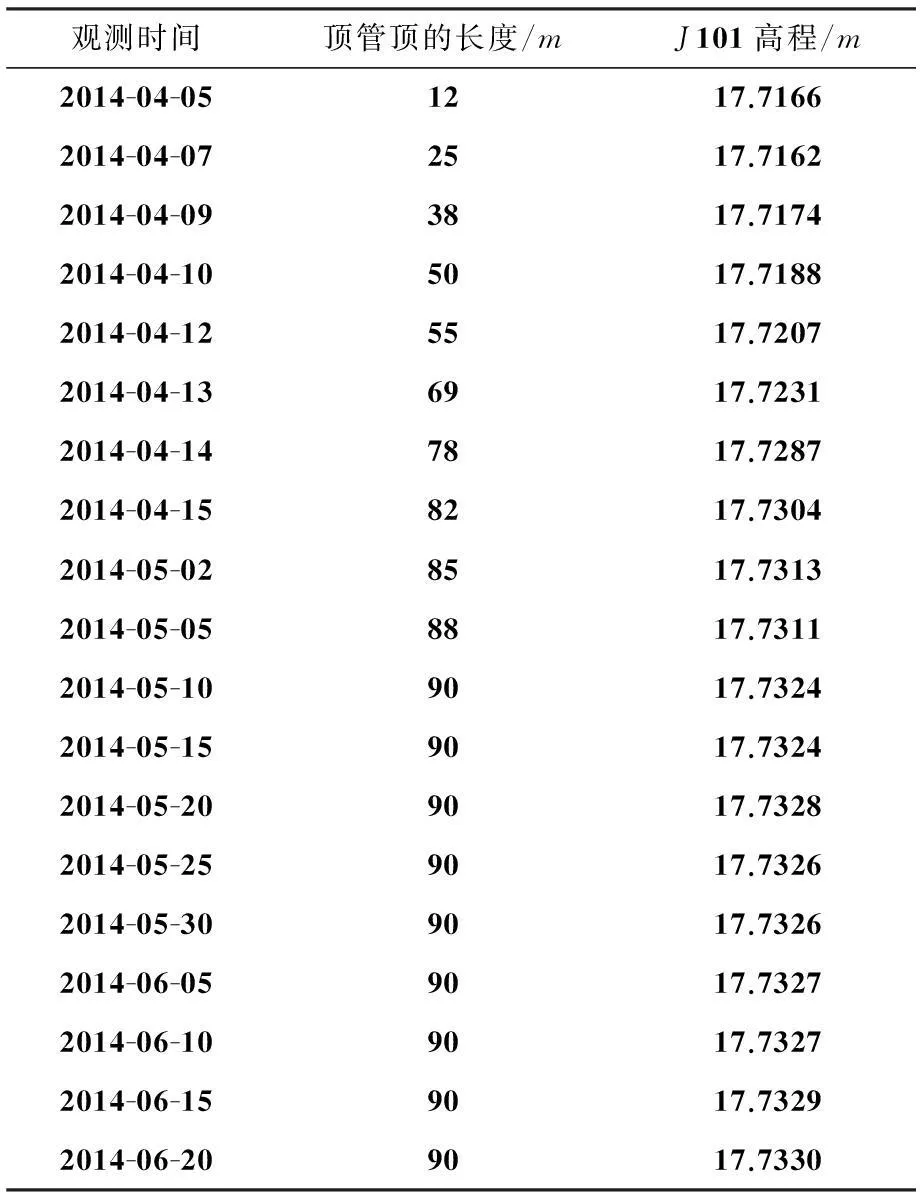
观测时间顶管顶的长度/mJ101高程/m2014-04-051217.71662014-04-072517.71622014-04-093817.71742014-04-105017.71882014-04-125517.72072014-04-136917.72312014-04-147817.72872014-04-158217.73042014-05-028517.73132014-05-058817.73112014-05-109017.73242014-05-159017.73242014-05-209017.73282014-05-259017.73262014-05-309017.73262014-06-059017.73272014-06-109017.73272014-06-159017.73292014-06-209017.7330

2.1回归建模

建筑物的沉降与时间、顶管顶长度等多个因素有关.采用回归方程进行预测值的计算，得出实测值和预测值之间的残差，可以为工程队安全施工提供依据.通过对本文中所选数据的分析，时间对下沉量的影响并不显著，所以在此只分析顶管顶的长度与下沉的关系.以J101点20次累计变化量为因变量Y，顶管顶的长度为自变量X进行回归分析，利用Eviews进行回归建模得到：

Y=0.000198X+17.71314

(10)

2.2残差检验

由残差序列的相关图(图1)可以看出扰动项有明显的自相关现象，并不满足古典回归假设.对残差序列可以进行进一步的信息提取.

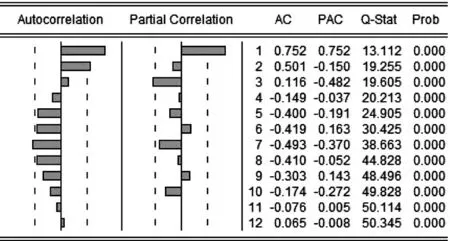
图1 残差序列相关图

2.3残差序列建模

由图1初步判断，可以建立ARMA(3,2)模型.剔除不显著的因子可以得到：

(11)

LM检验的结果：F-统计量为1.353798；残差平方根为5.700040；D-W统计量为2.1082.从结果可以看出残差序列通过了LM检验，已不存在自相关现象.

由表2可以看出所建立的回归和时间序列组合模型具有较高的预测精神.通过数据显示，相比单一的回归模型和时间序列模型，组合模型表现出了更强的可靠性.

表2监测点J101后五次的预测高程值和实际值的比较

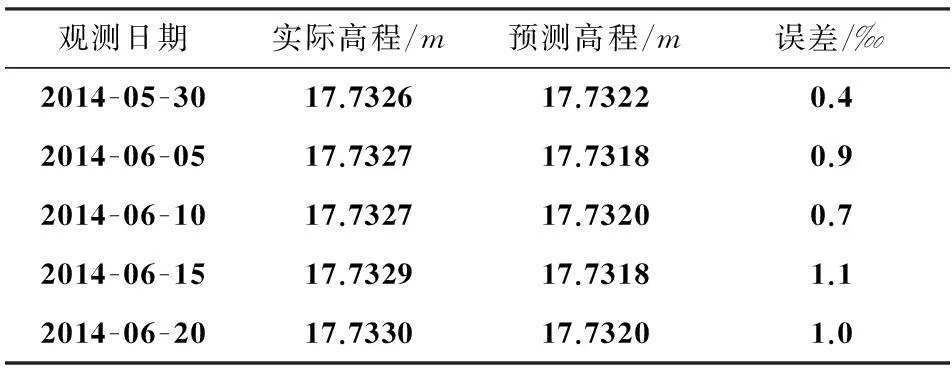
观测日期实际高程/m预测高程/m误差/‰2014-05-3017.732617.73220.42014-06-0517.732717.73180.92014-06-1017.732717.73200.72014-06-1517.732917.73181.12014-06-2017.733017.73201.0

3　结束语

本文通过对回归模型残差项的进一步分析，对残差序列利用时间序列分析进行建模，得到回归和时间序列的组合模型.相对单一回归模型来说，组合模型具有更好的预测精度和可靠性.

参考文献:

[1]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2003.

[2]史玉峰,孙保琪. 时间序列分析及其在变形数据分析中的应用[J].金属矿山,2004( 8):13-15.

[3]苗元欣.基于一元线性回归的变形监测数据处理与分析[J].山西建筑,2013,39(33) :206-207.

[4]李世平,郭泉河.采用ARMA模型对变形检测数据处理与预报[J].矿山测量,2013(5):70-72.

[5]陈伟清.回归分析在建筑物沉降变形分析中的应用[J].广西城镇建设, 2005, 22(4):249-251.

[6]张晓桐.计量经济学[M].北京：经济科学出版社,2003.

[7]张显云,杜宁.基于时间序列分析的动态变形预报[J].贵州大学学报：自然科学版,2013,30(4):54-57.

[8]吴芸芸,左延英.时间序列分析在变形监测中的应用[J].工程勘察,2012(1):69-72.

(编辑：姚佳良)

Application of a combination of regression and time series

model in deformation monitoring data processing

CHENG Shu， SUNChao， SHENYi ， LI Qiang

(College of Geomatics， Shandong University of Science and Technology， Qingdao 266590, China)

Abstract:In order to improve the accuracy of predicting the deformation, and abtain reliable and effective forecasting models, We further analyzed the residuals of the regression model,and built a time series model, a combination of the regression and time series models with the rasidual series sing eviews. Using this model, a set of measured data was analyzed and forecasted, and the deformation data and measured data are compared. The results showed that the combination model had better prediction accuracy and reliability.

Key words:regression analysis; time series; combined model

中图分类号：TV698.1

文献标志码：A

文章编号：1672-6197(2015)04-0053-03

通信作者:

作者简介：成枢，男，1334508055@qq.com;孙超，男，chaosun1989@163.com

收稿日期：2014-09-12