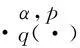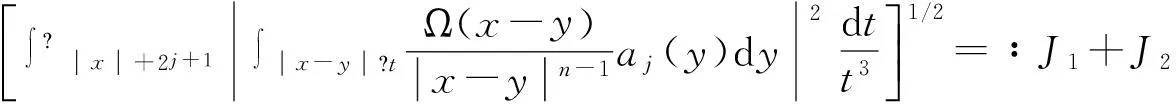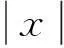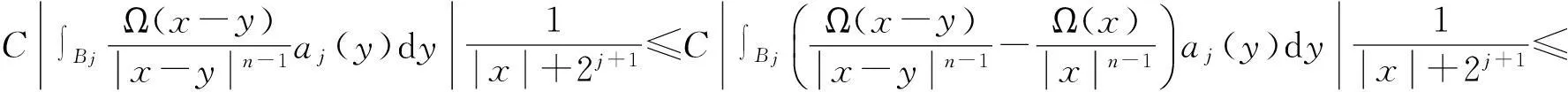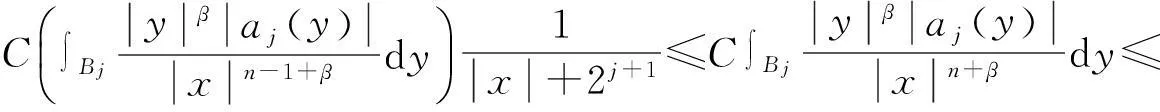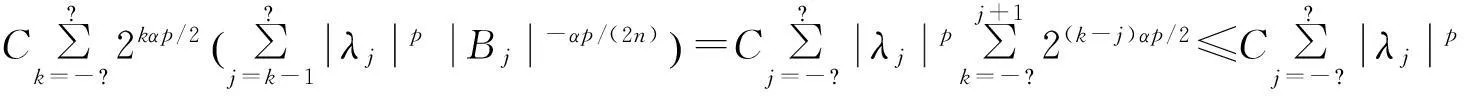变指标Herz型Hardy空间上的Marcinkiewicz积分
2015-12-16王洪彬
王洪彬
(淄博师范高等专科学校 数理科学系,山东 淄博 255130)
变指标Herz型Hardy空间上的Marcinkiewicz积分
王洪彬
(淄博师范高等专科学校 数理科学系,山东 淄博 255130)
摘要:Marcinkiewicz积分是调和分析中的重要算子,其有界性研究一直是调和分析中的重要课题之一. 应用其在变指标Lebesgue空间中的有界性以及变指标Herz型Hardy空间上的原子分解定理, 证明了Marcinkiewicz积分算子在齐次和非齐次变指标Herz型Hardy空间上的有界性.
关键词:Marcinkiewicz积分;变指标;Herz型Hardy空间;有界性

1 预备知识和记号
赋予如下Luxemburg-Nakano范数
则Lp(•)(Ω)是Banach空间, 称之为变指标Lp空间.

p(·)∶Ω→[1,)的集合, 使得p-=essinf{p(x)∶x∈Ω}>1,p+=esssup{p(x)∶x∈Ω}<.记p′(x)=p(x)/(p(x)-1). 令(Ω)为p(·)∈(Ω)并使得Hardy-Littlewood极大算子M满足Lp(•)(Ω)有界的指数函数p(·)的集合.
在变指标Lp空间中有如下几个重要的引理.
引理 1[4]设p(·)∈(n). 则存在常数C>0使得对所有n中的球B, 都有
引理 2[4]令p(·)∈(n). 则存在正常数C使得对所有n中的球B和所有可测子集S⊂B, 都有

其中δ1,δ2是常数且满足0<δ1,δ2<1(注意在整篇文章中δ1, δ2都同引理2中的一样).
引理3[1]令p(·)∈(n). 若f∈Lp(·)(n)且g∈Lp′(·)(n), 则fg在n上可积并且
其中rp=1+1/p--1/p+. 上述不等式被称为广义Hölder不等式.
下面我们给出变指标Herz空间的定义. 对于k∈, 令且Ak=BkBk-1. 记+和分别是所有正整数和所有非负整数的集合, 对k∈有χk=χAk, 若k∈+则且其中χAk是Ak的特征函数.
定义 1[4]令α∈, 0 在此基础上我们给出变指标Herz型Hardy空间的定义及其原子分解特征. 用S(n)表示n上的Schwartz空间, 它是由无穷可微且在无穷远处迅速递减的函数所构成的,S′(n)表示S(n)的对偶空间. 令GNf(x)为f(x)的grand极大函数, 其定义为 定义2[6]令α∈, 0 对于x∈我们用[x]表示小于等于x的最大整数. 定义3[6]令nδ2≤α<,q(·)∈(n)且非负整数s≥[α-nδ2].n上的函数a被称为中心(α,q(·))-原子, 如果它满足:(i) 对某个r>0有suppa⊂;;(iii) 对任意满足的多重指标β有∫a(x)xβdx=0.n上的函数a被称为是限制型中心(α,q(·))-原子, 如果它满足上述条件(ii), (iii)以及对某个r≥1有suppa⊂B(0,r). 引理 4[6]令nδ2≤α<, 0 其中下确界是对f的所有上述分解而取的. 设Sn-1为n(n≥2)上的单位球面,Ω∈Lipβ(Sn-1)(0<β≤1)是零次齐次函数且满足∫Sn-1Ω(x′)dσ(x′)=0, 其中对任意x≠0有年Stein[8]定义了如下与Littlewood-Paleyg函数相关的Marcinkiewicz积分算子: 其中 近来,Cruz-Uribe等[9]给出了Marcinkiewicz积分算子的Lp(•)(n)有界性,下面将其推广到变指标Herz型Hardy空间中. 定理1令Ω∈Lipβ(Sn-1)(0<β≤1/2),nδ2≤α 因此, 得 (1) 我们首先估计I1. 由aj的消失矩条件和广义Hölder不等式, 得 C2-kn+(j-k)β‖aj‖Lq(·)(n)‖χBj‖Lq′(·)(n). 综合J1,J2有 所以由引理1和引理2,有 ‖μ(aj)χk‖Lq(·)(n)≤C2-kn+(j-k)β‖aj‖Lq(·)(n)‖χBj‖Lq′(·)(n)‖χk‖Lq(·)(n)≤ (2) 因此, 当0 (3) 当1 (4) 现在我们来估计I2. 类似地,考虑p的两种情形. 当0 (5) 当1 (6) 结合式(1)和式(3)~(6), 有 因此, 定理得证. 参考文献: [1]KovácikO,RákosníkJ.OnspacesLp(x)andWk,p(x)[J].CzechoslovakMathJ, 1991, 41(4):592-618. [2]DieningL,HarjulehtoP,HästöP,et al.LebesgueandSobolevspaceswithvariableexponents[M].Heidelberg:Springer, 2011. [3]XuJS.VariableBesovandTriebel-Lizorkinspaces[J].AnnAcadSciFennMath, 2008, 33: 511-522. [4]IzukiM.BoundednessofsublinearoperatorsonHerzspaceswithvariableexponentandapplicationtowaveletcharacterization[J].AnalMath, 2010, 36(1): 33-50. [5]NakaiE,SawanoY.HardyspaceswithvariableexponentsandgeneralizedCampanatospaces[J].JFunctAnal, 2012, 262(9):3 665-3 748. [6]WangHB,LiuZZ.TheHerz-typeHardyspaceswithvariableexponentandtheirapplications[J].TaiwaneseJMath, 2012, 16(4): 1 363-1 389. [7]HarjulehtoP,HästöP,Lê ÚV, et al.Overviewofdifferentialequationswithnon-standardgrowth[J].NonlinearAnal, 2010, 72(12): 4 551-4 574. [8]SteinEM.OnthefunctionofLittlewood-Paley,LusinandMarcinkiewicz[J].TransAmerMathSoc, 1958, 88(2): 430-466. [9]Cruz-UribeD,SFO,FiorenzaA, et al.TheboundednessofclassicaloperatorsonvariableLpspaces[J]. Ann Acad Sci Fen Math, 2006, 31: 239-264. (编辑:郝秀清) MarcinkiewiczintegralsonHerz-typeHardyspaceswithvariableexponent WANGHong-bin (DepartmentofMathematicalandPhysicalScience,ZiboNormalCollege,Zibo255130,China) Abstract:Marcinkiewicz integrals are very important in harmonic analysis. The research on boundedness of Marcinkiewicz integrals has been one of important subjects in harmonic analysis. Using the boundedness of Marcinkiewicz integrals on variable Lebesgue spaces and the atomic decomposition characterizations of Herz-type Hardy spaces with variable exponent, we obtain the boundedness of Marcinkiewicz integrals on the homogeneous and non-homogeneous Herz-type Hardy spaces with variable exponent. Key words:Marcinkiewicz integral;variable exponent;Herz-type Hardy space;boundedness 中图分类号:O174.2 文献标志码:A 文章编号:1672-6197(2015)04-0016-05 作者简介:王洪彬, 男, hbwang2006@163.com 基金项目:国家自然科学基金资助项目(11171345);淄博师范高等专科学校研究课题(13xk023) 收稿日期:2014-12-04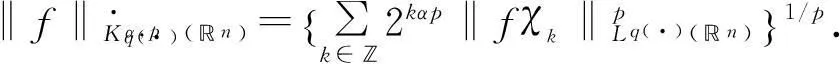
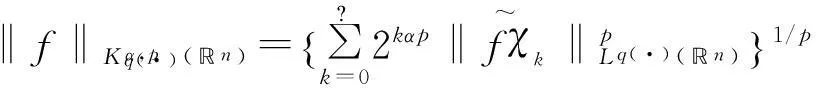
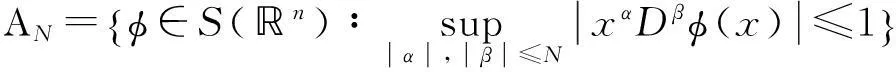

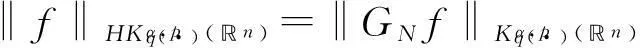

2 主要结论及证明