灵敏性编码重建磁共振成像与非笛卡尔k空间运动轨迹的研究

张连俊， 刘　刚

(山东理工大学 计算机科学与技术学院， 山东淄博 255049)



灵敏性编码重建磁共振成像与非笛卡尔k空间运动轨迹的研究

张连俊， 刘刚

(山东理工大学 计算机科学与技术学院， 山东淄博 255049)

摘要：对敏感性编码的磁共振成像并行重建方案进行了研究，实现了非笛卡尔采样k空间轨迹分析.在敏感图像信息中，由接收器线圈阵列采集的螺旋k空间数据被应用到欠采样数据集中以重构建无混叠重建图像.此外，由于网格算法具有前向估值和非正交采样数据伴随运算能力，被用来实现敏感性编码重建图像.研究发现，敏感性编码可减少用于磁共振成像实验的扫描时间，同时保持与下采样数据集的图像分辨率.最后，利用真实数据组计算验证了敏感性编码的性能，并分析了进一步提高计算速度的方法.

关键词：并行成像; 敏感性编码; 网格; 磁共振成像

磁共振成像(MRI)是一项新颖的医疗成像诊断技术.但由于制造快速切换的磁场梯度的技术困难，当前MRI扫描仪达到了数据采集速度的物理极限.未来的发展方向是通过减小扫描和重建的时间来提高运行速度.采取平行相控阵列线圈和平行重建方法可达到更快MRI成像的成像技术.1987年相控阵列线圈首次被用于减少相位编码[1]，可成比例的减少扫描时间量.在随后二十年MRI研究中，其它并行成像方案也有了长足的进步.在这些方案中最熟知的是敏感性编码法[2](SENSE)和空间谐波同时采集法[3](SMASH).SENSE与SMASH相比的优点是提供并行成像任意线圈的构造，但在信噪比(SNR)方面有额外损耗.尽管这两种技术都可以显著压缩扫描时间，但是对于欠采样数据变换图像，特别是在非正交的数据集的情况下，计算数据的密集的逆过程是必需的.针对此问题有人提出了一种正交重建方案[4]，该方案结合了快速傅立叶变换(FFT)以正向和反向网格运算，计算复杂度由N4降低到N2logN.这种方法使灵敏编码的影像实现了任意k空间采集模式[5].此外，为了优化SENSE的计算效率，计算中采用迭代方法[6-7].这种方法不会对SENSE成像方案的整体计算性能有很大的影响.本文利用网格化算法的敏感性编码来实现与非笛卡尔k空间轨迹的重建，对比其与“双瞳”的数据设置的性能.这些方法将完善目前SENSE的实施，并为实现三维核磁共振成像数据集的重建打下坚实的基础.

1　基于SENSE的MRI并行成像

磁共振并行成像常常是通过收器线圈阵列收物体数据成像的、收器线圈阵列主要用于提高图像的信噪比，减少数据采集时间，其中每个独立空间中的不同朝向的接收器线圈接收不同的数据集.公式(1)表示一个典型的核磁共振实验中的基带图像数据.

ρ(t)=∫d(r)S(r)e-iω(r)te-i2πk(t)tdr+ε(t)

(1)

式中：d(r) 是目标的坐标r处的磁化轨迹连续函数；沿着r的运动轨迹直接从磁共振成像扫描仪在k空间得到，S(r) 是接收器线圈的空间灵敏度分布； ω(r) 是位置r处B0磁场不均匀性；k(t) 是时间t的输入数据轨迹; ε(t) 是噪声项.公式(1) 表示k空间数据，线圈灵敏度分布和磁场的不均匀性的信息可用于并行图像形成三个基本组成部分，从多个独立的线圈所获得的数据可以集成到一个系统中.每个线圈接收的数据由Sl(r)加权, l = 1,..., L, 等等. 平行成像模型中的综合矩阵形式因此可表示如下(取l=3为例)：

(2)

式中：ρ1表示信号矢量从线圈1接收到的数据和图像矢量ρ通过叠加ρ1形成； SL是对角矩阵保持从第1个线圈的空间灵敏度曲线；F表示成像系统矩阵.

从上面的数学模型可知，并行成像是利用信号处理方法，减少扫描时间并获得k空间中的数据量，同时仍保持相同的空间分辨率，即k空间的相同区域仍有效的覆盖奈奎斯特敏感点与从相控阵列线圈所获取的数据.根据采样理论通用信号处理知识，任何并行成像方案将使得相位编码线的数目减少，之间的间隔是1/视场(FOV).在叠加计算重构图像时，采用了传统的FFT变换.图1中完全采样数据集和欠采样数据集重建的两个图像，相互比较证明了相位编码线数目的减少.

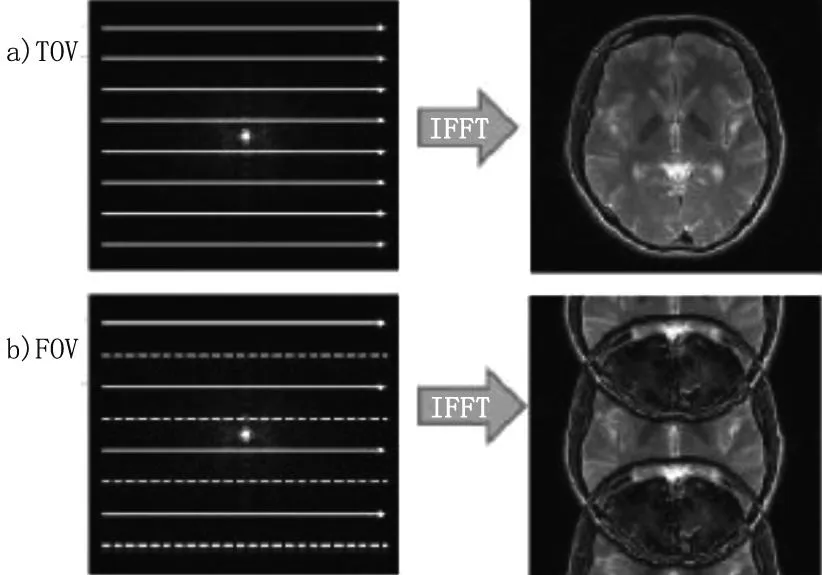
图1　完全采样和欠采样k空间分析

SENSE并行成像方案[5]结合上述叠加效应，可使多个线圈混叠信号具有更快的成像速度.以笛卡尔采样k空间为例，相位编码线之间的位置和距离在MRI实验前通常已知.从位置和距离能够准确的计算叠加在每个线圈的重构图像的量.假定扫描时间减小，加速因子为R，在FOV中的重建的图像将被缩小或折叠.对于相同因子R，FOV/R的位移像素值可得到一个重构象素的信号强度，叠加在目标对象叠加位置的强度为R-1倍.这使得SENSE能够求出图像的叠加强度并筛选出所需的值，如图2所示.

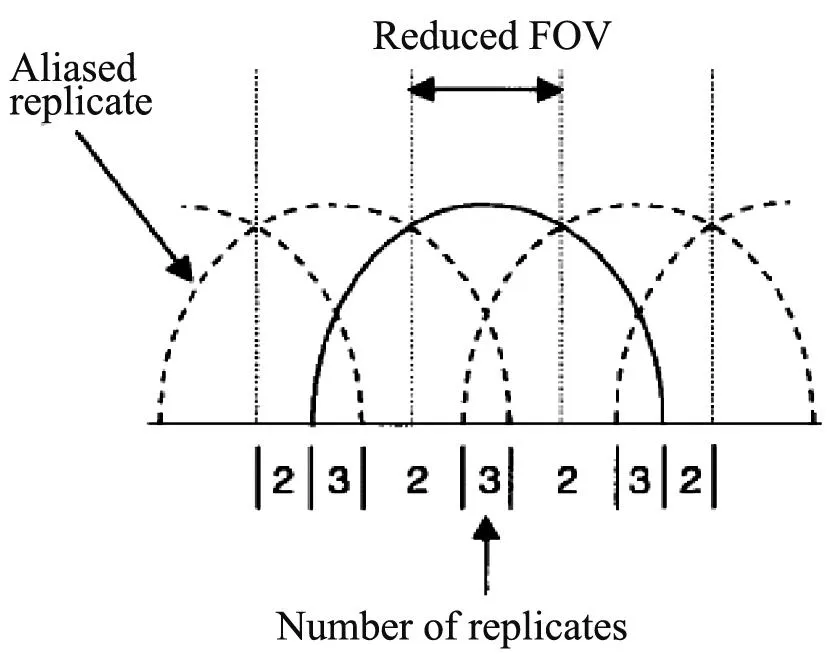
图2 SENSE并行成像方案数据重构

SENSE成像方案：为了获得全视场图像数据所需的图像，像素的图像值Ik(x，y)在相应的位置加权，线圈灵敏度分布为(x,yl)，其中l= 1，...，R，在位置(x，y)的与第k个线圈的信息的准确重构象素值如下：

Ik(x,y)=Sk(x,y1)ρ(x,y1)+Sk(x,y2)ρ(x,y2)+

…+Sk(x,yR)ρ(x,yR).

(3)

该方程可以转化成矩阵表示法，并形成重构图像，显示如图3所示.

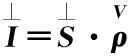
(4)

为了简化计算公式，在公式(4)中暂不考虑噪声相关性问题.根据矩阵理论，得出视场图像的灵敏度矩阵S.

(5)

从方程(5)可以看到，SENSE过程的“展开”功能由从广义矩阵求逆来实现.另外，值得注意的是SENSE重建算法需要FOV的图像的每一个像素位置，最终重构一个完整的视场图像.在SENSE重建的实际实施中，由于存储器的限制、计算速度瓶颈的影响，不采用传统 的矩阵S和SH广义矩阵求逆的解决方案，而采用以共轭梯度迭代的方法求解.

2　网格化算法

该网格算法通常采用不属于在k空间定期笛卡尔网格数据集进行处理.网格化方法允许收集和处理非笛卡尔数据集用于笛卡尔数据重建方法.如基于FFT的方案的运算方式，可以在没有多大修改时仍能应用.网格算法中所获得的螺旋形轨迹的数据是由第一次重新采样到笛卡尔采样网格的FFTW库来完成图像重建的.在重新采样的过程中，网格算法提供近似的伴随算子和向前计算算子.伴随算子和向前计算算子的概念表示如下：

(6)

(7)

式中：d(m) 为降界的k空间采样的数据；a(t) 表示插值窗函数的时间分割值；f(xn) 表示的是B0场的不均匀性参数；km表示第k-空间中的轨迹值.在这两个计算途径中，共轭算子计算是以图像数据的值和k-空间的轨迹作为输入，以笛卡尔网格点的k空间数据值作为输出.用向前算子计算时与此相反，取k空间数据的值和k-空间的轨迹作为输入，并输出每个对应的像素位置的图像值.虽然这两种运算不同，但图像重建的评值时都采用了共轭梯度法.

伴随算子的计算可以有以下三个步骤：第一步，在k空间中的每个数据点进行采样，以任意的采样函数来采样数据点，然后卷积用网格化的内核.在本文中利用凯塞贝塞尔函数被用作网格内核.第一步可以表示为下面的等式：

(8)

式中：d(kx,ky) 表示原始k空间数据点；S(kx,ky) 表示第k-空间采样函数；K(kx,ky) 表示凯泽贝塞尔网格内核. 理想的图像d(x,y) 实际上是通过与傅里叶卷积网格化模糊化的凯撒贝塞尔网格化内核来实现重建.第二步，对网格卷积的结果进行傅里叶变换，然后在笛卡尔网格点重新采样.这个步骤是将原始的螺旋k空间数据点和重新采样值变换到到相邻的笛卡尔网格点，在图像域中的相应的计算如下：

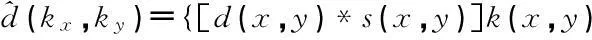
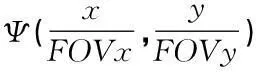
(9)

式中：d(x,y) 表示理想的图像数据；s(x,y) 表示图像域取样函数；k(x,y) 表示在图像领域的凯撒贝塞尔网格内核；ψ(x,y) 表示图像域重新采样函数.在第二步会出现不理想的因素，即螺旋形旁瓣通常引起采样图案的点扩散.为了抑制旁瓣的引入，在第三步骤修正图像的傅立叶变换的网格内核.

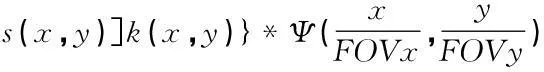
(10)

第三步引入阴影中的图像从而抑制从第二步中产生旁瓣.最后计算结果即是以共轭算子网格算法计算出的重建图像.

向前算子网格算法即是实现逆网格化，反转网格化计算中的每一个步骤.先从共轭梯度求解图像变换值，再估计在k空间相应的变换数据.从上面的网格化的过程中，很明显看出逆网格化的第一步骤应该是变迹，即取消在网格算法的最后一步的修正图像的效果.

(11)

逆网格的其余步骤是简单地在k空间中卷积和重新采样.与在共轭算子的那些对应步骤相对，这些步骤的唯一区别是从笛卡尔网格点估算在k空间中的螺旋轨迹的值.在k空间中数据的表达式如下.

K(kx,ky)]S(kx,ky)

(12)

有些文献[8-9]说明，密度补偿是必要的.而本文中使用的特定数据集没有采用密度补偿，而特定数据集采用密度补偿重建图像的分辨率，信噪比没有显著改善.在混叠失真较大时应加补偿，在计算中加上补偿因子即可实现.

3　数据分析与实验结果

图像重建的数据设定的是来自“ISMRM重建”的“双瞳”数据[10].12轴位图像的“双瞳”的数据源在腹部用躯干相控阵线圈采集.原始矩阵尺寸为320×320，图像采集采用梯度回波图像TE=3方式采集，用96×96采集矩阵调整为四种不同的尺寸，分别为64×64矩阵、128×128矩阵、256×256矩阵和512×512矩阵，以测试重建的有效性.同时还提供数据集与原来的数据集合成8螺旋行轨迹，具有20000像素点.k空间轨迹重建前后的图像见图4和图5，图中的灰色区域表示交错覆盖序列中的区域.四种不同尺寸的重构图像显示见图6至图9.

图4 图像重建前扫描轨迹图5 图像重建后扫描轨迹

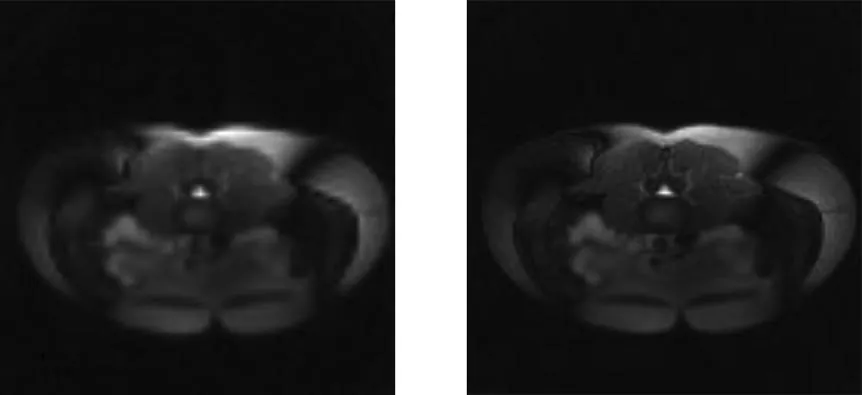
图6　64× 64图像重建图 7 　128× 128图像重建

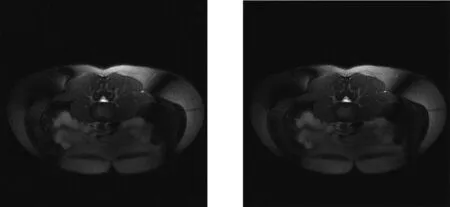
图8　256× 256图像重建图9　512× 512图像重建

上述实验分析表明，采用网格算法的SENSE并行成像方案能够有效地处理非笛卡尔k空间轨迹.在图7和图8中，对应于数据集的矩阵大小的图像分辨率比图6有所增加.然而在图8和图9之间图像的分辨率提高不显著，这是由于原始采集的数据集仅有320×320矩阵的大小.通过内插在k空间缩放矩阵大小不会显著改善图像分辨率.表1给出了SENSE方法实现的计算效率.估值计算时间大约是实际计算时间的90%以上，计算时间的差异主要是由于存储器大小影响.

表1SENSE实现的计算效率

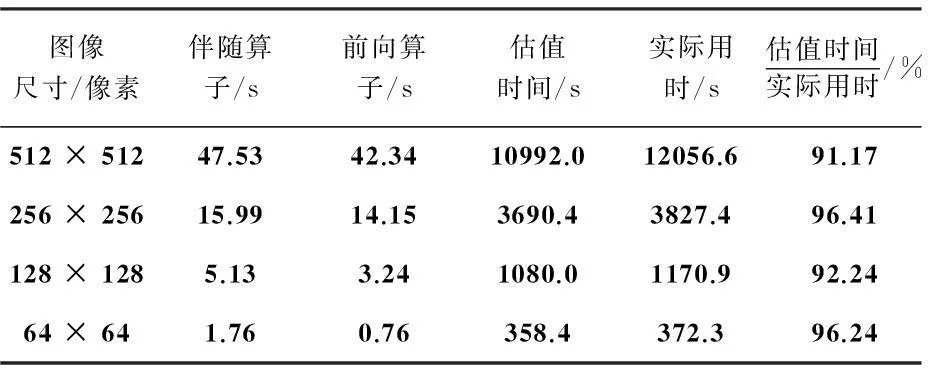
图像尺寸/像素伴随算子/s前向算子/s估值时间/s实际用时/s估值时间实际用时/%512×51247.5342.3410992.012056.691.17256×25615.9914.153690.43827.496.41128×1285.133.241080.01170.992.2464×641.760.76358.4372.396.24

4 结束语

利用网格化算法的SENSE并行成像，可使从任意k空间轨迹重建图像的效果提高，并提高重建图像的速度.通过来自多个接收器线圈的采样数据，可以有效地补偿失真.采用共轭梯度算法、正向和反向网格和FFT变换等组合方法可以降低计算复杂度.然而从图6到图9中可以看出，重构图像中包含少量的来源于给定数据集中的高斯白噪声，这可以通过将正则化与SENSE相结合来消除.这将不断完善目前SENSE处理方法，并为实现SENSE三维核磁共振成像数据重建打下坚实的基础.

参考文献:

[1]CarlsonJ.AnalgorithmforNMRimagingreconstructionbasedonmultipleRFreceivercoils[J].MagnReson, 1987,74: 376-380.

[2]PruessmannK.SensitivityencodingforfastMRI[J].MagnResonMed, 1999,42: 952-962.

[3]SodicksonD.Simultaneousacquisitionofspatialharmonicsfastimagingwithradiofrequencycoilarrays[J].MagnResonMed, 1997, 38: 591-603.

[4]PruessmannK.Advancesinsensitivityencodingwitharbitaryk-spacetrajectories[J].MagnResonMed, 2001,46: 638-651.

[5]BlaimerM,SmashS,GrappaP.Howtochoosetheoptimalmethod[J].TopMagnResonImaging,2004,15:223-236.

[6]LinF.Parallelimagingreconstructionusingautomaticregularization[J].MagnResonMed, 2004,51:559-567.

[7]FesslerJ.Toeplitz-basediterativeimagereconstructionforMRIwithcorrectionformagneticfieldinhomogeneity[J].IEEETransSigProc, 2005,53: 3393-3402.

[8]PaulyJ.Non-CartesianReconstruction[J].Lecturenote, 2007, 86:759-767.

[9]FangS,YingK,ZhaoL,etal.CohereregularizationforSENSEreconstructionwithanonlocaloperator[J].MagneticResonanceReview, 2010, 64(5):1414-1426.

[10]WuB,MillaneR,WattsR, et al.Priorestimate-basedcompressedsensinginparallelMRI[J].MagneticResonanceReview,2011,2011,65(1):83-95.

(编辑：姚佳良)

Researchofsensitivityencodingreconstructionfor

MRIwithnon-cartesiank-spacetrajectories

ZHANGLian-jun,LIUGang

(SchoolofComputerScienceandTechnology,ShandongUniversityofTechnology，Zibo255049,China)

Abstract:The sensitivity encoding (SENSE) parallel reconstruction scheme for magnetic resonance imaging (MRI) was studied and implemented with non-Cartesian sampled k-space trajectories in this report. The sensitivity map profile, field map information and the spiral k-space data collected from an array of receiver coils were used to reconstruct un-aliased images from under-sampled data. The gridding algorithm was also implemented with SENSE due to its ability in evaluating forward and adjoins operator with non-Cartesian sampled data. SENSE has the special capability to reduce the scanning time for MRI experiments while maintaining the image resolution with under-sampling data sets.We also analyzed the performance of SENSE with real data set and identified the computational issues that need to be improved for further research.

Key words:parallel imaging; SENSE; gridding; MRI

中图分类号：391.4

文献标志码：A

文章编号：1672-6197(2015)04-0021-04

作者简介：张连俊，男，zhlj@sdut.edu.cn

收稿日期：2014-09-29