多维数据立方体的分块与压缩设计

何 平

（湖北襄阳职业技术学院，襄阳441021）

多维数据立方体的分块与压缩设计

何 平

（湖北襄阳职业技术学院，襄阳441021）

目前提出的关于多维数组存储组织的有效方法，没有有效解决存储空间的浪费和存储维内部层次信息问题，导致存储浪费。采用Fragment分块方法将高维空间进行降维存储，分别分为稀疏维和密集维，数据块建立在稀疏维成员组合的基础之上，即将稀疏维相同的度量数据存储在一个数据块中，每个数据块有唯一的标识。对多维数据立方体进行了分块处理，并获得了每个数据块的标识。对于是否需要创建该数据块，只需要在生成数据文件时判断该数据块是否为空，若为空则不需要创建该数据块；若不为空，则创建该数据块。最后给出多维数据立方体的压缩算法。

多维数据；分块设计；降维存储；数据库；高维空间；压缩算法

1 引 言

目前虽然已经有大量文献提出了关于多维数组存储组织的有效方法，但是这些方法都没有完全解决存储过程中存在的一些问题。第一，数组过于稀疏会导致大量存储空间的浪费，而使用压缩技术不但会增加存储的复杂性，而且会给OLAP查询处理带来额外开销［1］。第二，大多数多维数组存储结构没有充分考虑如何存储维内部层次信息，而事实上许多OLAP操作多是针对维内部层次进行的［2］。所以需要对与数据仓库存储结构相关的技术进行深入的学习研究，对原有的存储模式进行改进，克服目前存在的问题。

2 多维数据立方体的分块设计

对多维数组进行存储通常是将其线性化为一维数组，由坐标确定数据单元的位置后再进行顺序存放。不过这种方法不利于数据的多维分析，所以采用分块存储方法，首先将数据立方体划分为小的立方体，然后以小的立方体为基本单位进行存储，从而可以保持数据的多维性。

2．1 分块算法

采用Fragment分块方法，即将高维空间进行降维存储。如多维数据立方体建立在n维空间Ω之上，则将其划分为两个不相交的子空间Ψ（m维）和Φ（n－m维）。对于子空间Φ，计算每一个可能的维组合，每一个组合对应子空间一个m维立方体。因此，如果从空间Ω（D0，D1，……，Dm－1，Dm，……，Dn－1）选取S＝｛D0，D1，……，Dm－1｝作为空间Ψ的坐标系，则Ω空间中任一个点Q（p0，p1，……，pn－1）将映射到Ψ中的点Ψ（q0，q1，……，qm－1）和Φ中的点Φ（r0，r1，……，rn－m－1）之中，有如下关系：

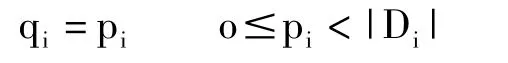
式中｜Di｜是维Di的基数，0≤i＜m。

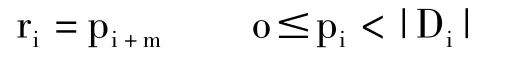
式中｜Di｜是维Di的基数，0≤i＜n－m。

2．2 分块设计

采用文献［3］提出的稀疏维和密集维划分策略对维空间进行划分。对于某一空间内大多数维的成员组合都没有度量值，可用空间位置填充量比较低，则可将这些维设为稀疏维。而密集维是每一种维组合都可能包含一个或多个度量值的维。这种划分方法，首先保持了数据的多维性，符合数据仓库和OLAP的基本要求；另外将维度划分为稀疏维和密集维，便于数据的压缩存储，提高空间利用率。

例如对于一个包含四个标准维：Time、Type、Region和Product的多维数立方体来说，空间Ω为｛Time，Type，Region，Product｝；设Time和type为密集维，region和product为稀疏维，则两个子空间分别为Ψ｛Time，Type｝和Φ｛Region，Product｝。图1显示的是一个二维数据块表示密集维Time和Type中的数据值，Time中的成员为J、F、M和Q1，Type维中的成员为Retail和Batch。图2显示的是将整个多维数据立方体划分后得到的所有数据块，Region维中的成员为West、East和South，Product维中的成员为P1、P2和P3。

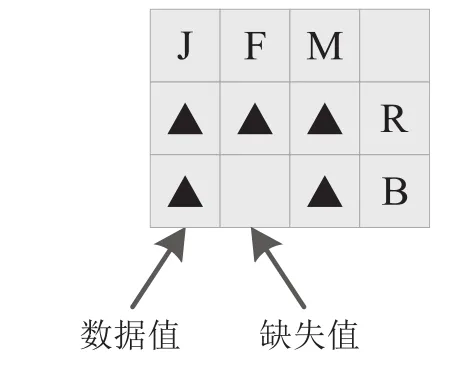
图1 用于Time和Type的二维数据块

3 多维数据立方体的分块

对多维数据立方体进行分块存储既保持了数据的多维性，又可以提高系统的I／O操作效率［4］。采用Fragment分块算法，将高维数据降维存储。多维数据立方体中的维度被划分为稀疏维和密集维，分别对应两个低维空间，数据块建立在稀疏维成员组合的基础之上，即将稀疏维相同的度量数据存储在一个数据块中，每个数据块有唯一的标识。

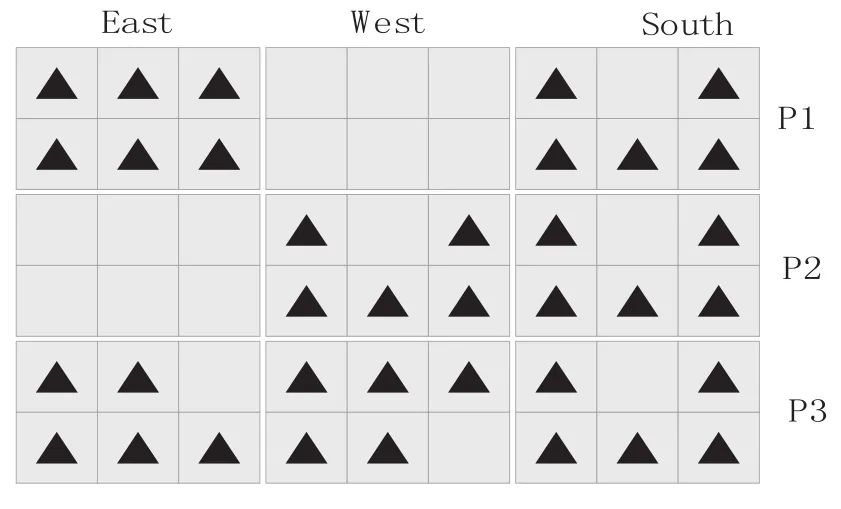
图2 划分后的多维数据立方体

实现多维数据立方体分块的类图如图3所示。在按照稀疏维组合对多维数据分块以后，又对每个块按照密集维最高层成员组合对其进行子块划分，每个数据块中子块的大小和个数都是统一的［5］。

多维数据立方体分块类图中各个类的功能如下：

（1）SubBlockHead类是子块头信息类，定义了一个getSubHead（）方法用来根据稀疏维最高层次成员组合情况获得子块ID。

（2）SubBlockDataField类是子块数据域类，YearSales（）方法、QuarterSales（）方法和MonthSales（）方法分别用来获得年销售量、季度销售量和月销售量，Sales（）方法则用来获得所有层次的销售量，并使用getfieldString（）方法将所有数据转换成字符串的形式返回。

（3）SubBlock类是创建子块的类，是SubBlock-Head类和SubBlockDataField类的聚合，即每个子块包含子块头和数据域两部分，getSubBlock（）方法将子块转化成字符串形式返回。

（4）BlockDataField类是数据块中的数据域类，每个数据块包含一个数据域，这些数据域由若干个子块组成。该类将数据块中包含的所有子块对象放入ArrayList，并使用getBlockDataField（）方法将子块对象列表转换成字符串类型返回。

（5）BlockHead类是数据块头信息类，数据块头信息中关键的内容是数据块的ID，getBlockHead（）方法根据密集维组合信息计算并以字符串形式返回数据块的ID。

（6）Block类是数据块类，每个数据块包括数据块头信息和数据域两部分，所以该类由BlockHead类和BlockDataField类聚合而成，getBlock（）方法将数据块转换成字符串形式返回。

图3 多维数据立方体分块类图

4 多维数据立方体的压缩

将多维数据立方体的维空间按照稀疏维和密集维的规则进行划分以后，会获得如图2所示的一些空白数据块。对这些空白的数据块不需要再进行存储，而只需存储有效的数据块和数据块标识［6－7］。

对多维数据立方体进行了分块处理，并获得了每个数据块的标识。对于是否需要创建该数据块，只需要在生成数据文件时判断该数据块是否为空，若为空则不需要创建该数据块；若不为空，则创建该数据块。具体算法如下：

输入：所有稀疏维成员编码

（1）确定稀疏维成员的组合；

（2）查找度量数据表，是否存在该组合对应的度量数据；

（3）若该稀疏维成员组合没有对应的度量数据，则返回重新进行下一种成员组合的判断若；该稀疏维成员组合有对应的度量数据，则进行下一步；

（4）创建该稀疏维组合对应的数据块；

（5）将有效数据块添加到数据块列表中，返回继续进行下一种成员组合的判断，直到所有组合情况判断完毕。

输出：有效数据块列表。

5 结束语

对于多维数据立方体的存储主要有两种模式：关系表和多维数组。关系表模式建立在RDBMS的基础之上，具有成熟的存储和查询技术支持，但是不能表现数据的多维性，不利于数据仓库的OLAP操作。多维数组与多维数据立方体在形式上具有一致性，适用于数据的多维分析，但是其存储技术还不完善。对多维数组进行存储时，一般情况下是将多维数组线性化为一维数组后再进行存储，这样就又打乱了数据的多维性，文章提出的分开与压缩算法对多维数据存储有一定的应用价值。

［1］ Paul Gray，Hugh J Watson．Present and Future Directions in Data Warehousing［J］．The DATA BASE for Advances in Information System，1998，29（3）：83－90．

［2］ Matthis Jarke，Manfred A Jeusfeld，Christoph Quix，Panos Vassiliadis．Architecture and Qualityin Data Warehouses：An ExtendedRepositoryApproach［J］．Information Systems，24（3）：229－253．

［3］ Nenad Jukic．Modeling Strategies and Alternatives for Data Warehousing Projects［J］．COMMUNICATIONS OF THE ACM，2006，49（4）：83－88．

［4］ Venky Harinarayan，Anand Rajaraman，Jeffery D Ullman．Implementing Data Cube Efficently［J］．ACM SIGMOD Record，1996：205－216．

［5］ Tatsuo Tsuji，Akihiro Hara，Ken Higuchi．An Extendible Multidimensional Array System for MOLAP［J］．SAC，2006：503－510．

［6］ E JOtoo，DoronRotem，SridharSeshadri．Optimal Chunking of Large Multidimensional Arrays for Data Warehousing［J］．DOLAP，2007（11）：25－32．

［7］ TatsuoTsuji，AkihiroHara，TeruhisaHochin，Ken Higuchi．An Implementation Scheme of Multidimensional Arrays For MOLAP［J］．Computer Socitey，2007：1－6．

Design on Block and Compression of Multidimensional Data Cube

He Ping
（Hubei Xiangyang Vocational and Technical College，Xiangyang 441021，China）

The methods proposed by the multidimensional array storage organization have no effective solution to solve the storage space waste and internal hierarchical information storage．This paper adopts Fragment partition method to fragment the block to high－dimensional space dimension reduction of storage，which is respectively divided into sparse and dense，block of data is set up based on sparse group，i．e．the same sparse dimension measurement data is stored in a data block，each block has a unique ID．The block processing of multidimensional data cube is conducted and the identity of each data block is obtained．For the data block creating，the situation，whether the data block is empty or not，should be judged when the data file is generated．The data block is not be required if it is empty，and if not null，then the data block should be created．The multidimensional data cube compression algorithm is given as well．

Multidimensional data；Block design；Dimension reduction storage；Database；High dimensional space；Compaction algorithm

10．3969／j．issn．1002－2279．2015．04．010

TP301

A

1002－2279（2015）04－0039－03

何平（1976－），女，湖北省襄阳市人，讲师，主研方向：计算机网络、物联网，数据库。

2014－12－25