让几何直观促进学生的数学思考

◆江苏省常熟市张桥中心小学 杨佳玲

◆江苏省无锡市锡山教师进修学校 严育洪

让几何直观促进学生的数学思考

◆江苏省常熟市张桥中心小学 杨佳玲

◆江苏省无锡市锡山教师进修学校 严育洪

几何直观具有形象具体、简单抽象的双重特点，将抽象的数学语言与直观的图形有机结合，有助于学生理解数学知识的本质，促进学生的数学思考。要真正发挥几何直观对数学学习的促进作用，在日常教学中要注重培养学生的几何直观意识，循序渐进地培养学生画图表征问题的能力，注重培养学生借助图形思考问题的能力，让画图思考、读图分析成为学生的自觉行为。

几何直观；学生；数学思考

几何直观是《义务教育数学课程标准（2011版）》（以下简称“课标”）提出的十大核心概念之一。“课标”指出：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用。”据此，我们不难发现，几何直观不仅指直接观察，更重要的是依托图形进行深入思考与分析，打开思维，找到方法，解决实际问题。

阿蒂亚说过：“几何直观是领悟数学最有效的渠道。”数学知识的抽象表达，学生理解起来有难度，要把握其本质更是难上加难。借助几何直观，将抽象的数学语言与直观的图形巧妙对接，有助于学生直观地理解数学，把握数学知识本质，促进学生的数学思考，找出解决问题的思维突破口。

在整个基础教育阶段数学学习过程中，几何直观发挥着重要作用。教师应有意识地培养学生的几何直观能力，让几何直观成为一种意识、能力、思维方式。根据平时教学实践，笔者认为，要实现让几何直观促进学生的数学思考的目标，可以从以下三方面着手。

一、注重培养学生的几何直观意识

意识的培养取决于价值的认同，因此，几何直观意识培养的首要任务就是教师在日常教学中要积极引导，让学生充分体验几何直观的作用和价值。

1.沟通数学知识与几何图形的联系，在知识学习中体会价值。

小学生的思维以形象思维为主，在他们的眼中，抽象、严谨、概括的数学知识可能是枯燥而难懂的。借助几何直观，可以将抽象的概念、算理、法则等变得形象而生动，这不仅能降低学生理解数学知识的难度，而且有助于学生把握数学知识的本质。

【案例1】苏教版教材三年级上册《倍的认识》一课中，教师让学生用黑白圆片代替物品创造一幅“2倍”关系图。学生作品纷呈，展示出了3的2倍、5的2倍、10的2倍……教师提问：“像这样表示‘2倍’的关系图，可以画出多少呢？”学生回答：“很多很多，无数。”教师追问：“能不能想个办法把这么多的图用一个图表示出来呢？”有学生指出，可以用线段图表示，接着在师生对话中完成了线段图（如图1）。教师又问：“在这个框里可以填哪些数？”学生回答：“什么数都可以。”

图1

在教学本环节之前，学生从大量的例证中感知了“倍”的概念本质。让学生利用黑白圆片创造“2倍”关系图，一方面，可加深学生对概念的理解；另一方面，在此基础上，借助线段图表征概念，摒弃了所有非本质属性，有助于促进学生对概念的准确理解，提升了学生对“倍”的认识。

几何直观不仅是沟通学生形象思维与抽象数学概念的桥梁，也是学生发现算法、理解算理的突破口。小学数学计算教学常常借助几何直观进行，以图为载体，可以将算理有形地显示出来，有利于学生感知与理解算理。

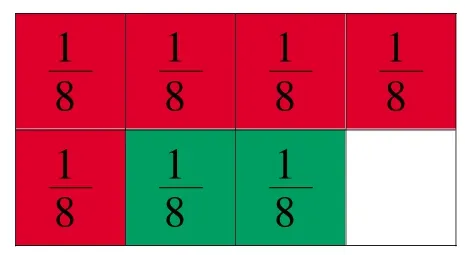
图2

【案例2】苏教版教材三年级上册《同分母分数的加法和减法》一课中，教师先让学生根据例题列出算式再引导让学生借助长方形涂一涂、想一想、算一算。根据提示，学生纷纷将长方形的涂上红色，长方形的涂上绿色（如图2）。在学生独立思考、组内讨论有结果后，教师提问：“你的计算结果是多少？”学生说是教师追问：“你是怎么想的？”有学生说：“看出来的，图上一共涂了有学生说：“红色部分有5个绿色部分有2个 5+2=7，一共7个结合图示，教师指出表示5个表示2个一共涂了7个

教师接着引导学生观察得数的分子和分母与两个加数的分子和分母各有什么关系，学生一下子就发现了同分母分数的加法的算法，即分母不变，分子相加。

虽然教材没有给出计算法则，但借助直观图形，教师适时引导点拨，学生就能自己总结算法、理解算理，并能有条理地表达计算思路。“形”与“算式”结合起来，让学生明晰抽象的算理，观察发现出算法。可见，利用图形直观让学生明白、理解抽象的算理是行之有效的手段。

2.借助几何图形描述和解决问题，在应用中体会价值。

让学生体会几何直观的作用，最为直接的方式就是让学生应用几何直观。在教学中遇到可以利用图形来描述的问题，教师可以不必急于给出解决问题的方法，而是鼓励学生借助直观图形分析思考问题，帮助学生不断积累思考的经验，理解几何直观的价值与作用。

【案例3】苏教版教材三年级上册有这样一道练习题（如图3）：

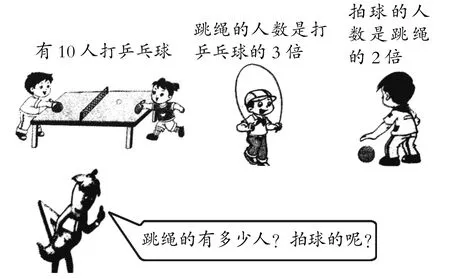
图3

日常教学中，教师通常引导学生先根据“跳绳的人数是打乒乓球的3倍”求出跳绳人数，再根据“拍球的人数是跳绳的2倍”计算出拍球的人数。基于学生对条形图的认识与理解，笔者认为，在讲解这题时不妨引入直观图示（如图4）。借助直观图形，学生对这题中数量间的关系会有更为深入的认识，能进一步打开学生的思维。观察图示，学生不仅能看出打乒乓球的人数与跳绳人数、跳绳人数与拍球人数之间的倍数关系，还能看出拍球人数是打乒乓球人数的6倍，从而找到不同解题方法。有了这样的体会，教师时时引导学生回顾解题过程，说说体会和收获，有助于加深学生对几何直观的体验，体会价值。

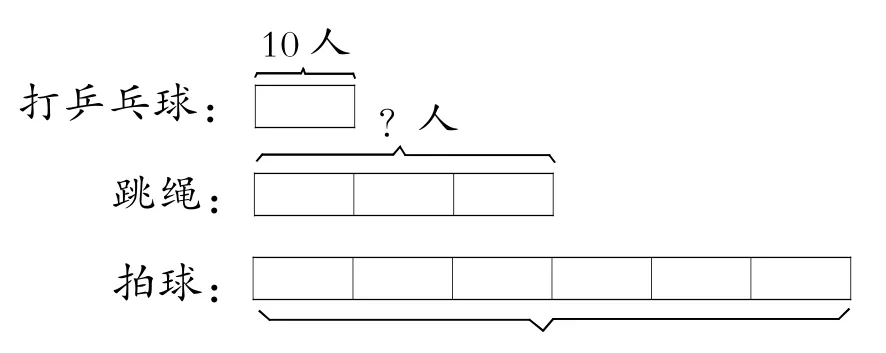
图4

二、注重培养学生画图表征问题的能力

学生对图形的感悟是一个长期的、循序渐进的培养过程，画图表征问题的能力也不是一蹴而就的。为此，苏教版教材为学生搭建了许多图示平台，各个年级教材中都有出现。在日常教学中，教师应注重结合相关内容，循序渐进地培养学生画图表征问题的能力。

一、二年级学生以动作思维和形象思维为主，数学学习大多要依靠实物、图片等载体，通过看一看、摆一摆、分一分等活动才能领会、掌握。因而，在日常教学中，教师要适当进行抽象和提炼，由实物直观向图形直观过渡，让学生多接触直观图，为学习画图表征问题积累经验。

例如，《5的乘法口诀》一课中的“想想做做4”（如图5），创设了青蛙和兔子跳格子的情景，引导学生在数轴上分别表示出5个3相加的和，5个4相加的和，并写出相应的乘法算式。这样的活动，既加深了学生对乘法口诀含义的理解，又让学生初步体会了画图描述问题的方法。

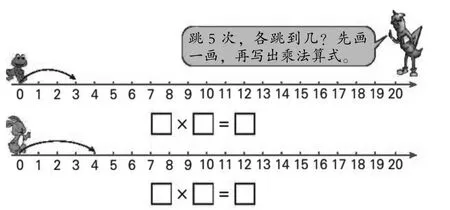
图5

教材还编排了许多图示题（如图6），教师可以结合这些题目，培养学生看图理解题意、读图分析数量关系的能力，在解决问题的过程中，不断积累读图分析的能力，感悟直观图示是表征问题的一种常用方法。

运用线段图或示意图直观地表示抽象的数学问题是利用图形直观描述问题最直接的方式。苏教版教材将有关线段图、示意图的内容安排在三、四年级，一方面是因为学生具备了一定的几何知识基础，另一方面是数学学习内容越来越抽象，更需要几何直观提供支撑。自三年级（上）开始，结合解决问题的策略教学，学生开始系统地学习画线段图。

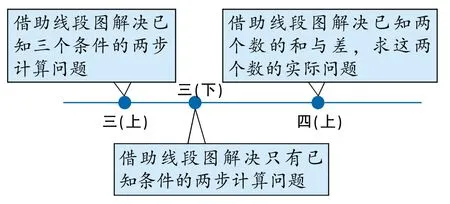
伴随题目抽象程度与难度的不断提升，在“读题——补图——画图——读图”的过程中，学生的数形转换能力不断提升，画图表征问题的水平不断提高。有了画线段图表征问题的基础，四（下）解决问题的策略，例如，教学用画示意图的策略解决有关面积计算的实际问题，从一维图示向二维图示过渡，学生的画图能力有了阶段性提升。

在之后的教学中，一方面要结合具体教学内容和实际问题，继续训练学生画图表征问题的能力；另一方面要注重在回顾反思中内化这一策略，让画图成为学生的自觉行为。

三、注重培养学生借助图形思考问题的能力

华罗庚说：“数以形而直观，形以数而入微。”数形结合是一种重要的解决问题的方法。根据小学生的思维特征，借助几何直观解决实际问题，化抽象为直观，便于学生理解题意，分析数量关系，找到解题的突破口。因而，教师在教学中不仅要培养学生读图、画图的能力，更要培养学生借助几何直观思考分析问题的能力。

【案例4】苏教版教材五年级下册《解决问题的策略》单元例2，要求计算按学生已有的知识经验，他们通常会采用先通分，再计算的方法。显然，对于这一题来说，通分的方法不算繁琐，但如果题目改变为通分的方法就变得麻烦。因而教材将本题安排在转换策略的教学单元，旨在利用几何直观帮助学生打开思维，创造性地解决问题。教材首先引导学生观察发现这一算式的特点，这些分数每一个都是前一个的一半，进而引导学生把正方形看作单位“1”，再将算式中的加数填入图中相应位置（如图7）。巧妙地借助几何直观，将算式与图形联系起来，学生就比较容易发现：最后分出的图形与剩下的图形相等。复杂的计算问题转化成简单的数学计算问题，加法计算转化为减法计算有了这样的体会与感悟，解决类似的问题也就有了方法。

图7

在日常教学过程中，我们还发现，几何直观不仅是解题的突破口，还是打开学生思维之门的金钥匙，借助直观图示能发现不同解题方法。

【案例5】苏教版教材四年级下册《解决问题的策略》单元有这样一道“练一练”：小营村原来有一个宽20米的长方形鱼池。因扩建公路，鱼池的宽减少了5米，这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米？（先在图中画出减少的部分，再解答）（如图8）

图8

如果没有直观图形，对于小学生而言，发现其中的数量关系难度很大。画出示意图之后，学生不仅理清了解题思路，还找到了多种解题方法。

现在？平方米20米▲5米 减少了150平方米▲▼▼方法1 150÷5=30（米）30×20=600（平方米）600-150=450（平方米）方法2 150÷5=30（米）20-5=15（米）30×15=450（平方米）

?

在交流中，可以了解到方法1与方法2的解题关键是发现分割前后长方形的长不变，方法3的关键是发现原来长方形的宽与减少的长方形的宽呈倍数关系，那么分割前后，3个长方形的面积也成倍数关系。如果没有几何直观的支撑，分割前后3个长方形边长与面积的对应关系是很难被学生发现的。

几何直观是“用图说话”，是形象思维与抽象思维的结合，是一种洞察数学知识本质的重要方式。在日常教学中，作为一线教师，应充分挖掘素材，直观地反映和揭示数学本质，帮助学生理解掌握数学知识，感悟数学思想。

几何直观还是一种创造性思维和重要的数学思想方法，在学生解决问题的过程中有着不可替代的作用。为此，我们要为学生提供积累几何直观经验的时间与空间，提升其几何直观能力，让几何直观促进学生的数学思考。

[1]曹培英.跨越断层,走出误区：“数学课程标准”核心的实践解读之四——几何直观（上）[J].小学数学教师,2013（6）：25-36.

[2]曹培英.跨越断层,走出误区：“数学课程标准”核心的实践解读之四——几何直观（下）[J].小学数学教师,2013（7,8）：12-20.

[3]冯崇和.几何直观：探索解决小学数学问题的重要手段[J].小学数学教与学,2014（11）：7-10.

[4]林晓捷.在数学教学中运用几何直观[J].小学数学教与学,2014（11）：18-20.

[5]王琴.数与代数领域强化几何直观的策略——一道英国小学数学毕业试题测试分析与思考[J].小学数学教与学,2014（11）：15-17.

[6]宋健泳.小学生几何直观能力发展的几个阶段[J].小学数学教师,2015（3）：66-69.

（编辑：胡 璐）

严育洪，江苏省特级教师，江苏省教育厅小学数学学科领军人物，江苏省“333高层次人才培养工程”学术技术带头人，无锡市有突出贡献中青年专家，无锡市教育专家委员会委员，无锡市锡山教师进修学校培训部副主任。曾发表多篇教育论文，出版多本教育专著，其专著入选教育部基础教育课程教材发展中心中小学图书馆（室）推荐书目，并被评为年度无锡市第十届哲学社会科学优秀成果，并被引出到马来西亚出版发行。曾参加“国标本”苏教版小学数学教材编写，近百次赴全国各地讲学；杨佳玲，江苏省常熟市张桥中心小学数学教师，曾获常熟市把握学科能力竞赛一等奖，辅导学生撰写的多篇数学小论文分别获市一、二等奖。主要研究方向：中年级数学教学。

G623.5

A

1671-0568（2015）34-0070-04