发挥策略在应用性问题建模教学中的作用

◆江苏省扬州市东关小学 韦波富

发挥策略在应用性问题建模教学中的作用

◆江苏省扬州市东关小学 韦波富

解决应用性问题的过程是建模的过程，其中数量关系的分析是核心。解决问题的策略在建模的不同阶段发挥着不同的作用。借助相应的策略可以理顺对应信息、引领建模方向、发现数量关系、同化认知结构和求解数学模型。

建模教学；应用性问题；策略

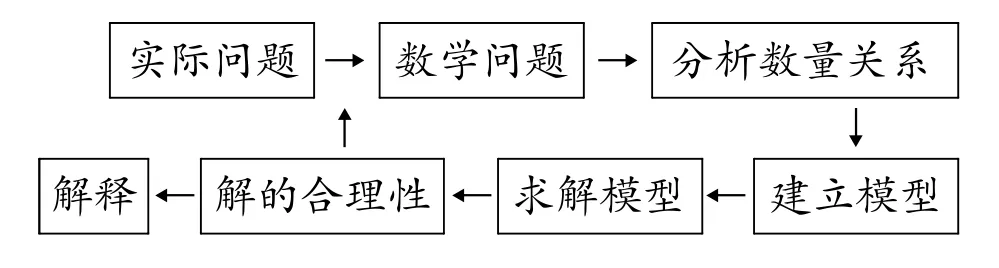
应用性问题教学的本质是建模。建模一般经过以下几个步骤（如图）：对实际问题进行观察、分析；将实际问题抽象、简化为数学问题；在数量之间建立某种关系，即建模；求解该数学问题；验证结果是否正确，正确则建模完成，否则从头开始。新版苏教版教材解决问题策略单元的展开的顺序与建模过程大体相同，即在呈现一个实际问题后，先弄清题意，明确已知条件和所求问题；再分析数量关系，确定先算什么再算什么；算出答案后还应做到检验和反思。其中，数量关系反映的是条件之间、条件与问题之间关联性的结构表达式，是解决这一问题的数学模型。而在建构数量关系模型的过程中，解决问题的策略和方法起着推波助澜的重要作用。

一、借助策略理顺对应信息

传统应用题呈现的是完备的结构，数量关系很快就能找到。但现实生活中，信息的出现可能是杂乱无章的，或是隐蔽的，可能会充斥着很多无关的信息。因此，在解决问题时，学生要学会借助策略对信息进行整理和筛选，从纷繁复杂的情境里提取有用的信息，将现实问题转换成数学问题。

建模就是要发现信息间的某种规律，从而构建起一个关系式。理顺信息的对应关系是建模初始阶段的关键工作。这种对应关系主要是指它们之间的某种关联性，包括条件与条件之间的对应关系、条件与问题之间的对应关系。

列表或摘录是梳理信息的有效策略。它适用于信息比较复杂、关系比较模糊的问题。它的最大特点就是通过整理使得两个相关的不同数量之间、或几个相同数量之间、条件与问题之间的对应关系比较清晰，比如时间和路程的对应关系、时间与时间的对应关系、时间路程与速度的对应关系等。条件与相应问题的对应关系有时通过从条件想起建立；有时通过从问题想起策略有选择的获取，避免多余信息的干扰，发现缺少的信息。信息的这种对应方式体现了高度的有序性，便于比较，利于发现数量之间的关系。

理顺信息的对应关系所采取的策略不是唯一的。有时需要借助画图的策略，画图能直观地显示题意，有条理地表示数量；有时还需要借助表演或画示意图加以厘清，如相遇问题，运动的物体从一个变为两个，情境中的信息量大，对应关系复杂，表演或画示意图再现问题中的情景是一个很好的选择。

二、借助策略引领建模方向

解决问题都有一定的思路，思路体现学生的思维过程。“从条件想起”与“从问题想起”是解决问题的两种思路，也是解决问题的基本策略。

“从条件想起”就是通过条件之间的组合，步步逼近所要解决的问题，即从已知推出未知。苏教版三年级（上）“小猴帮妈妈摘桃，第一天摘了30个，以后每天都比前一天多摘5个。小猴第三天摘了多少个？”解决这类问题学生可以从条件想起：根据“第一天摘了30个”和“以后每天都比前一天多摘5个”可以求出第二天摘的个数；再根据“第二天摘的个数”与“以后每天都比前一天多摘5个”可以求出第三天摘的个数。由此可见，在策略指引下的建模是有根据的、有序的。教材中还安排了根据已知条件提出问题的训练，如“买了3盒钢笔，每盒10支，买的圆珠笔比钢笔多18支”，学生可以根据前两个条件提出“一共买了多少支钢笔？”这一问题，再根据钢笔的支数和第三个条件进而提出“一共买了多少支圆珠笔？”这一问题。这种接力式的建模方向直指所要提出或解决的问题。

“从问题想起”则是通过对问题的分析，寻找解决问题所需要的条件，它与“从条件想起”的策略相比则是反方向的。苏教版三年级（下）（如下图）如果从条件想起会走很多弯路或者不必要走的路，根据问题则会很快找到所需要的条件，策略的价值凸显无疑。学生根据问题首先建立一个主干模型：带来的钱-用去的钱=剩下的钱；然后再根据问题中剩下的钱“最多”这一要求，找到相应的条件求出用去的钱。教材中安排了根据问题寻找、补充条件的训练，目的就是理解、掌握建模的思路。教学中还可以将一些例题或习题改编成一个条件不完备的开放性问题，引导学生自觉运用“从问题想起”的策略发现问题和解决问题。

两种策略都指向于数量关系模型的建构，每种策略都有适用解决的问题。但在使用的过程中不是孤立的，往往是两种策略综合起来使用。有些问题既可以从条件想起，也可以从问题想起。从条件想起时要瞄准所要解决的问题，从问题想起还要联系、照顾情境中的条件，这样才能快捷、准确建模。教学时要引导学生学会表述解决问题的建模思路，促使学生的思维从直观感知上升到数学理解。

三、借助策略发现数量关系

在解决问题时，分析数量关系是从“数学问题”到“用数学方法解决”的桥梁，对于比较复杂或不够明朗的数量关系，教师要引导学生利用画图等表征方式进行分析和发现。如苏教版二年级（上）P8例4：小英做了11朵花，小华比小英多做3朵，小华做了多少朵？教学时可以画示意图发现数量关系。用圆圈代替花，先表示出小英做的朵数，再表示出小华做的朵数。在画的过程中领悟到这样的关系：小英做的朵数+3=小华做的朵数。苏教版三年级（上）P73第3题：18个小朋友站成一排，从左往右数，芳芳排在第8，从右往左数，兵兵排在第4，芳芳和兵兵之间有多少人？从字面表达上学生很难发现其中的数量关系，老师可以引导学生用△或○表示18个人，在图中找出芳芳和兵兵的位置，这时其中的数量关系显现无疑。

画线段图是解决问题的常用策略。新版苏教版教材非常重视线段图教学，从早期直条图的孕伏渗透到实际的线段图的操作运用，学生逐步了解线段图这一几何形式对解决问题的直观帮助。苏教版三年级（下）有这样一个问题：一条裤子28元，一件衬衫的价钱是一条裤子的3倍。买一套衣服一共要用多少钱？学生可以从条件想起或问题想起运用已有的经验解决问题：28×3=84（元），28+84=112（元）。在此基础上指导学生画线段图表示裤子、村衫的价钱，从而发现数量之间新的关系：1+3=4，28×4=112（元）。

列表整理也是发现数量关系的重要策略，通过对列表整理后的条件和问题信息进行比较，能发现信息之间的内在联系，有利于构建数量关系模型。有时候，数量信息是以图画形式呈现的，排列很有条理，这时可以引导学生对图中的信息进行分析比较，寻找到解决问题的突破口。苏教版三年级（上）解决问题策略单元P77有这样一道思考题（如下图），从条件怎样想？学生无从下手。这时可以引导学生对题中的两个条件进行比较，从比较中发现数量之间的关系：73元和49元里面巧克力的数量是相同的，相差的钱就是相差的两盒饼干的钱。

四、借助策略同化认知结构

原有的应用问题的结构、解决方法对学生解决新问题有着重要基础作用和经验参考。将新问题转化为熟悉的问题，或将原有的经验应用于新问题的解决，需要借助策略的支撑。

转化是把一个数学问题变更为一类已经解决或比较容易解决的问题，从而使原问题得以解决的策略。替换与转化有着同样的功能，它适用于条件关系复杂，没有直接的方法可解的问题。苏教版六年级（上）P68（如下）通过分析学生可以建立这样的数量关系模型：6个小杯的容量+ 1个大杯的容量=720毫升，小杯的容量=大杯的怎样求出1个大杯的容量和一个小杯的容量呢，可以将大杯替换成小杯，或将小杯全部替换成大杯，替换后都变成小杯或者都变成大杯，把两种量与总量之间的复杂数量关系转化为一种量与总量之间的简单数量关系。

数学课程标准指出，要处理好面向全体与关注个体差异的关系，鼓励和提倡解决问题策略的多样化。一方面培养学生的应用意识和能力，另一方面打通各种策略之间的联系，实现互联互通。如上面问题的教学时让学生独立思考，调动已有的经验通过自主建模解决问题。学生提出各自的策略，可以通过画图解决，也可以列方程解决，还可以运用替换的策略解决。这样的教材编排打通了各种策略之间的关系，让学生体会到策略运用的灵活性。通过解决问题的过程，学生的认知结构会得到调整和重组，使新问题的解决策略纳入到原有的认知结构中。

行程应用题是从一个物体的单向运动到两个物体的同时相向运动，其数量关系是不变的，都是用速度×时间=路程，不同的是相向运动时数量关系变为：速度和×相遇时间=总路程。教学时要通过分析理解这一数量关系，再通过比较将这一关系与单向运动的情形进行贯通，实现认知结构的同化。

五、借助策略求解问题模型

数学课程标准（2011版）在课程设计思路中指出，要“使学生体验从实际背景中抽象出数学问题、建构数学模型、寻求结果、解决问题的过程”。可见，求解模型是感悟模型思想的一个方面。算式、方程及其他数学表达式都是解决问题的模型，表现形式不同，寻求结果的策略也会有差异。算式的结果可以通过四则运算的规则进行计算得到。方程背后的核心思想，一是建模——布列方程；二是化归——解方程，解方程就是运用等式的性质将多元方程变为一元方程，将复杂的一元方程变为简单的一元方程。有些解决实际问题的模型实质上是一个不定方程，如苏教版五年级（上）P94问题：王大叔用22根1米长的木条围成一个长方形花圃，怎样围面积最大？解决这个问题第一步要做的事就是建模，即（长+宽）×2=22米，而求解这一模型的策略就是列举。

策略的教学和应用贯穿于解决应用问题的全过程。列表、画图等策略在建模的初始阶段可以帮助整理信息、明晰关系；从条件想起、从问题想起等策略可以引领建模的方向；替换、转化等策略可以将复杂的问题化归为简单的问题或者基本的模型；列举等策略可以在求解复杂数学模型的时候发挥特有的作用。同一个策略往往在解决问题的不同阶段发挥着不同的作用。同时，策略的教学和应用还贯穿于学生不同的学段，从低年级开始渗透，逐步积累运用策略帮助建模的经验。

（编辑：胡 璐）

本文为江苏省“十二五”规划课题（重点自筹 批准号B-b/2013/02/281）“用建模思想指导小学数学应用性问题教学的实践研究”研究成果。

韦波富，中学高级教师，江苏省特级教师，江苏省数学学会常务理事，扬州大学教育硕士兼职导师。

G623.5

A

1671-0568（2015）34-0020-04