复杂城市交通网络拥堵传播的改进SIS模型

张俊锋，马昌喜，吴 芳，蒲 菡，贾富强

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

复杂城市交通网络拥堵传播的改进SIS模型

张俊锋，马昌喜，吴 芳，蒲 菡，贾富强

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

为深入分析城市交通网络拥堵动态演进过程，建立了交通拥堵传播的改进SIS模型（传染病模型）。模型根据目标节点自身受随机因素的影响、其邻居节点的状态和影响能力以及不同状态节点间的耦合强度，动态计算目标节点由畅通变为拥堵又恢复畅通的概率，并进一步考虑了不同交通状态的传播时间对拥堵传播的影响。基于BA(Barabási-Albert)无标度网络对传播过程进行仿真，拥堵随时间的演化与相关研究一致，验证了模型的有效性。仿真结果表明：根据作用节点属性的不同，随机因素对拥堵的初始规模、传播速度及传播稳定状态的阻塞水平具有不同的影响能力；不同状态节点间的相互作用对拥堵传播具有重要作用；畅通状态与拥堵状态平均传播时间的比值对拥堵传播的影响存在阈值；不同状态传播时间的波动性对拥堵传播速度、平衡态阻塞水平具有一定影响。

BA无标度网络；交通拥堵传播；改进SIS模型；复杂城市交通网络；仿真分析

0 引言

随着我国经济的快速发展和城市化进程的加快，交通拥堵问题日益凸显，严重影响着城市交通系统的运行效率，给城市发展和人们的生活带来了诸多不便。城市交通系统是一个复杂巨系统，研究过程中发现仅仅对某些局部数据进行分析，对于缓解交通拥堵、提高交通网络的运行效率是远远不够的[1]，而迅速发展起来的复杂网络理论，为研究交通系统的复杂性提供了一个新的视角。

国内外学者对于复杂网络理论在交通系统中的运用已展开了部分研究。Moreno Y.等对BA无标度网络中由点和边的拥堵所引起的网络相继故障进行了研究[2]。Arrowsmith D.等指出随着网络拓扑结构从随机网络至无标度网络的转变，网络的表现力逐步恶化，负荷趋于局部化[3]。吴建军等根据车辆路径选择行为研究了不同网络拓扑结构和交通量产生率对拥堵传播的影响[4]，并基于点能力动态更新的模型研究了城市交通网络的级联失效过程[5]。孙会君等研究了具有群落结构的无标度网络上的交通动力学[6]。Zheng J.F.等研究了匀、异质交通需求和匀、异质能力分配下复杂交通网络的拥堵和效率[7]。Qian Y.S.等在考虑道路交通状态的基础上对复杂城市交通网络级联失效进行了研究[8]。李树彬等运用改进的中观交通流模型分析了复杂网络上的交通传播动力学特征和传播规律[9]。王正武等通过构建城市道路交通网络灾害蔓延动力学模型，分析了城市道路交通网络节点失效与节点连接强度、节点度及自修复因子的相关性[10]。杨泳等结合基本图法和三相交通流理论，构建了考虑迟滞现象的MCTM模型，对突发事件下快速路通行能力下降导致交通拥堵的形成及消散过程进行了研究[11]。刘新全基于贝叶斯网络推理，融合驾驶者出行先验及出行信息，研究了道路网络级联失效的演变机理及演变过程[12]。

综合来看，现有研究大多集中在对网络拓扑结构、网络流量负荷与交通拥堵之间的关系进行分析，而对拥堵传播过程研究较少。为了更好地进行交通拥堵的管理与控制，有必要对拥堵传播的影响因素及其作用规律进行研究。高自友等指出在实际的交通出行中，阻塞在交通网络中向相邻的路段和节点进行传播，类似于病毒在复杂网络中的传播[13]。基于这样的思想，本文根据交通流传播的特点，建立了一种交通拥堵传播的改进SIS模型。基于BA无标度网络对模型进行仿真，实验过程中拥堵随时间的演化与相关研究一致。同时本文还进一步比较分析了相关影响因素的作用规律，可为交通拥堵控制策略的制定提供一定的理论参考。

1 问题描述与建模

1.1 城市交通网络拓扑结构

城市交通网络由交叉口和连接它们的街道组成，其中交叉口或小区对应节点，街道对应边[1]。定义交通网络的拓扑结构为G=(V,E)的无向网络，其中V是节点的集合，E是边的集合。G可以用一个N×N的邻接矩阵(aij)N×N表示，N为网络节点数，节点i与节点 j之间存在连接关系，则aij=1，否则aij=0。节点i的度ki定义为与节点i连接的其他节点的数目。

1.2 模型分析

SIS模型中，节点被划分为两类：易感节点（对应畅通节点）和染病节点（对应拥堵节点）。染病节点作为传染源，以概率λ把传染病传给易感节点，而染病节点本身也会以一定的概率 μ被治愈。易感节点一旦被感染，就变成新的感染源[14]。由于交通系统自身的复杂特性，交通拥堵的传播具有与SIS模型中传染病传播不同的特点：

（1）交通网络中节点的状态并不是固定不变的，而是在畅通与拥堵两种状态之间来回变化。由于交通环境的不确定性[15]，即使没有拥堵节点的“感染”，畅通节点本身也可能自发地变得拥堵，成为传染源。而且由于所处交通状态不同，这种不确定的随机因素对拥堵节点和畅通节点的作用效果并不相同。

（2）并非只存在拥堵向畅通的单向传播，处于不同状态的节点之间存在相互影响：拥堵节点会引起周围节点交通负荷的增加从而可能引发周围原本畅通的节点变得拥堵；而由于周围畅通的节点对拥堵节点交通流的吸引作用，经过一段时间，拥堵节点也有可能变得畅通。同时，由于不同状态节点间交通流的耦合程度不同，它们相互影响的能力也不同。

（3）与SIS模型“接触感染”的方式不同，交通拥堵的传播需经过一定的时间。

1.3 模型建立

节点的度表示其直接连接节点的数量，反映了其在交通网络中传递交通流的能力，可以描述其对相邻节点的直接影响能力[16]。定义t时刻节点i由畅通状态转变为拥堵状态的概率为。

其中：

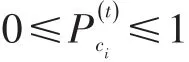
式（1）中，等号右边第一项表示邻居节点中拥堵节点对i的影响。α为畅通节点对拥堵节点的耦合强度，反映了拥堵节点对畅通节点的影响能力，与系统交通流状态和相关交通管理与控制的措施有关，α∈(0,1)。等号右边第二项表示t时刻随机因素在节点i畅通状态下对其的影响概率。例如，由于车流离散，交通流量短时间内的突然增大、非机动车和行人流的干扰、突发的交通事故、交通设施的偶发故障等，都可能使原本畅通的节点变得拥堵；而交通流量间歇地减小、交通秩序的恢复等有利于节点保持畅通。根据文献[17]，路网内交通总量一定时，城市道路交通网络中所有道路发生拥堵的概率满足高斯分布，设。

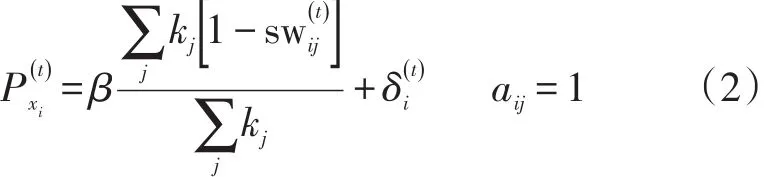
其中：

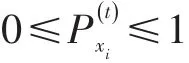
式（2）中，等号右边第一项表示邻居节点中畅通节点对i的影响。β是拥堵节点对畅通节点的耦合强度，反映了畅通节点对拥堵节点的影响能力，与α类似，β∈(0,1)。等号右边第二项表示t时刻随机因素在节点i拥堵状态下对其的影响概率。与类似，设。由于和对应于不同的交通状态，因此它们是相互独立的。

节点状态发生变化后，会将这种状态向相连节点传播，记节点i至节点 j拥堵的传播时间为tcij，拥堵消散的传播时间为。此处以正态分布对它们进行研究。

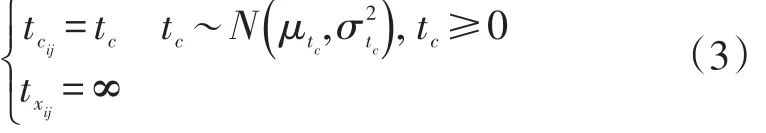
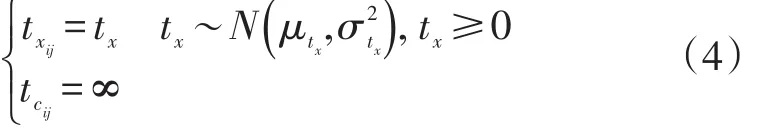
节点i变为拥堵状态，其影响传播至节点 j并对其发生作用的时刻记作；节点i变为畅通状态，其影响传播至节点 j并对其发生作用的时刻记作。

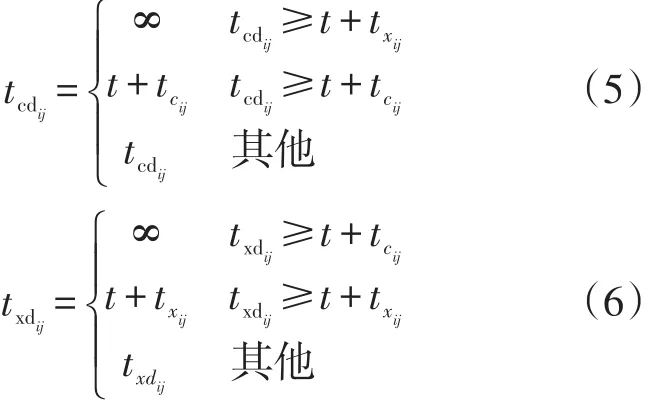
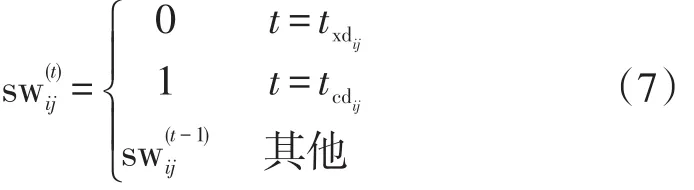
2 交通拥堵的衡量指标及仿真步骤

定义阻塞系数J来衡量网络交通性质，在t时刻：

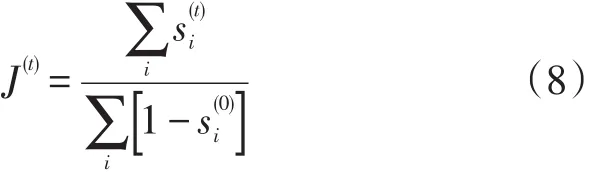
J体现了网络整体的阻塞水平，其大小反映了交通拥堵的整体规模，其增长的快慢反映了交通拥堵蔓延的速度。

模型的仿真步骤为：

3 仿真结果分析

以BA无标度网络作为复杂城市交通网络的拓扑结构模型[5]，利用Matlab R2010b连续仿真200步，文中结果为独立实验30次后的平均结果。仿真结果显示交通拥堵随时间的发展总体呈S型曲线，与文献[4]和文献[5]中失效节点（对应拥堵节点）随时间变化的规律一致。对相关参数不同取值进行研究，仿真结果符合实际传播中的现象。

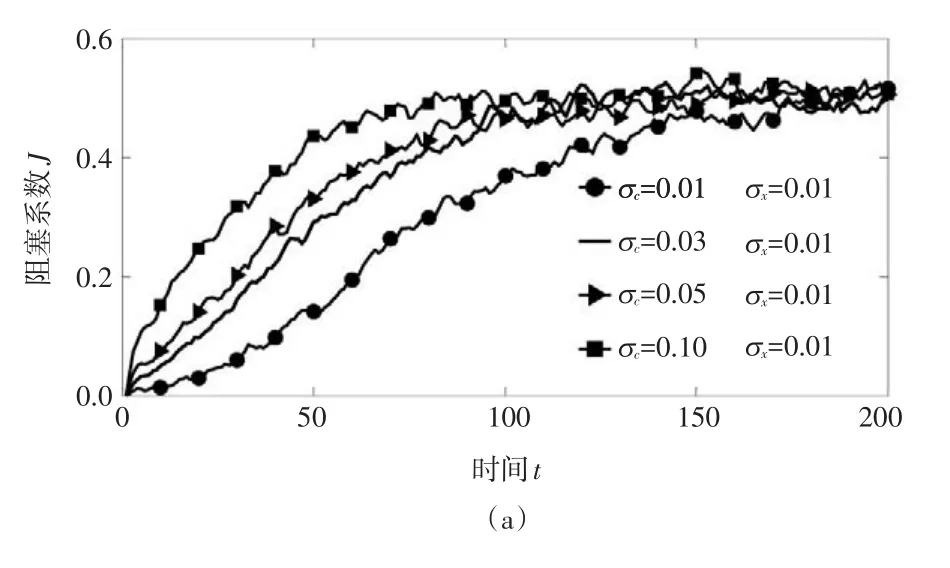
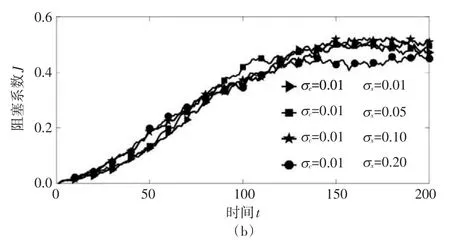
图1 不同σc与σx下阻塞系数J随时间变化趋势

3.2 α与β的影响

其他参数相同的情况下，对拥堵节点和畅通节点之间的耦合强度α和 β的不同取值进行仿真，仿真结果如图2所示。

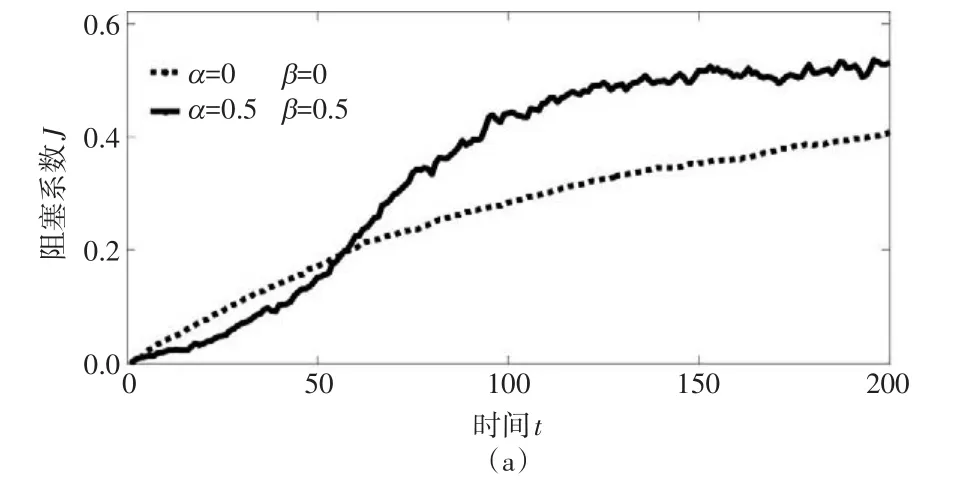
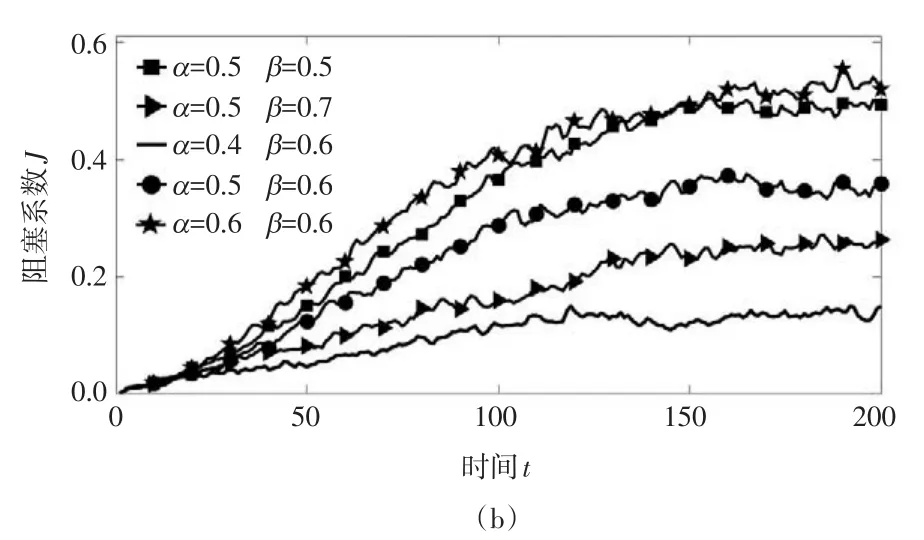
图2 不同α与β下阻塞系数J随时间变化趋势

从图2可看出，α和β的取值对交通拥堵传播的速度和网络平衡状态的阻塞水平有很大的影响。

图2（a）显示，当α=0,β=0（此时节点的状态完全受随机因素影响，与邻居节点无关）时，随时间的推进，阻塞系数缓慢增加。而当α≠0, β≠0（图中均取值0.5）时，传播初期由于畅通节点的作用抑制了阻塞的发展，而随着拥堵的传播，拥堵节点的作用增强，导致拥堵快速扩大，超过了单纯由随机因素引起的拥堵发展速度，经过一段时间后系统最终达到平衡。这说明节点间的相互作用对拥堵的传播起着重要作用，与3.1节的分析一致。

图2（b）显示，当α与β同时增大时，拥堵传播速度和网络平衡态阻塞水平都会增大；当α保持不变，随着β的增大，拥堵传播的速度和其最终平衡状态的阻塞水平都会降低；而当β＞α且二者差距一定时，α越小，拥堵传播的速度和其最终平衡状态的阻塞水平减小得越明显。

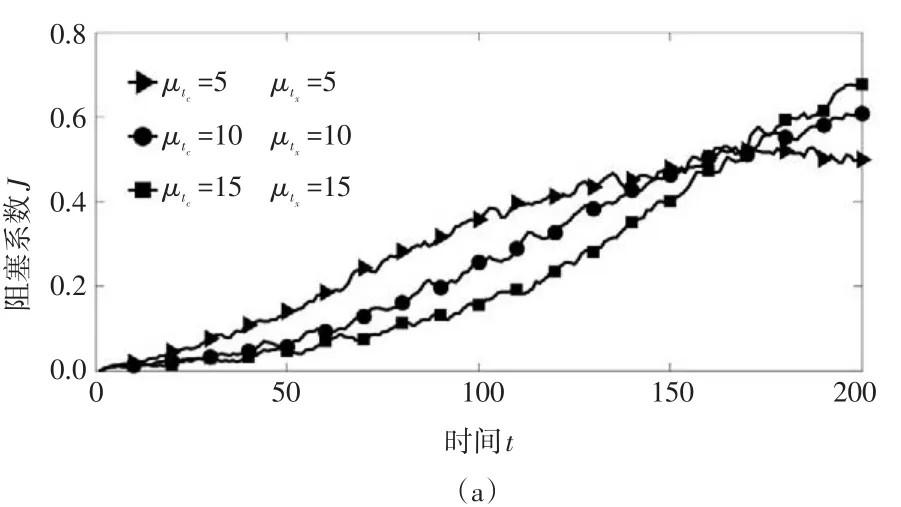
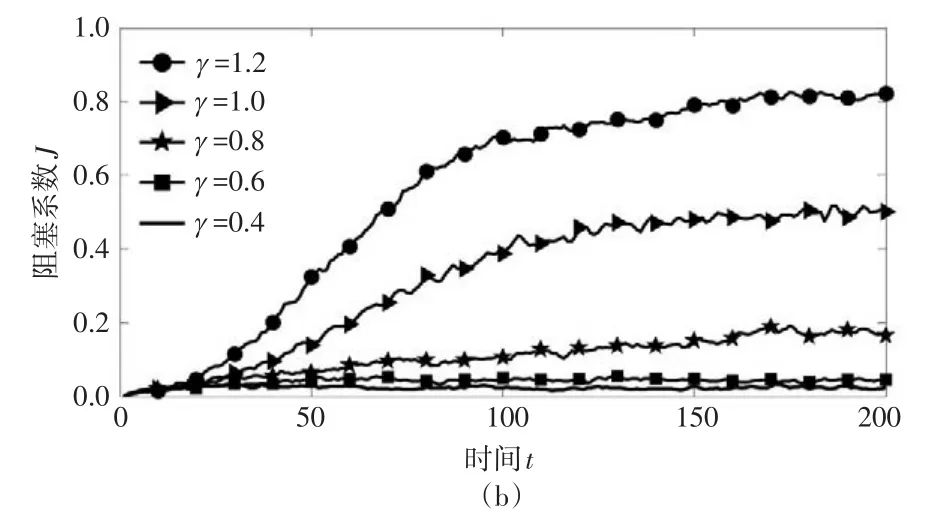
图3 不同与下阻塞系数J随时间变化趋势

在其他参数相同的情况下，对拥堵态和畅通态传播时间的标准差的不同取值进行仿真，仿真结果如图4所示。

图4 不同与下阻塞系数J随时间变化趋势

4 结论

本文根据交通拥堵传播的特点构建了交通拥堵传播的改进SIS模型。通过仿真，验证了模型有效性，并进一步研究了不同影响因素的作用规律，结果表明：

（2）节点间的相互作用对拥堵的传播起着重要作用，减小拥堵节点对畅通节点的状态的干扰能力α、增大畅通节点对拥堵节点的影响能力β可以有效抑制拥堵传播。

（3）随着畅通状态与拥堵状态平均传播时间比值γ的减小，拥堵的传播速度和平衡态阻塞水平迅速下降，但γ的影响存在阈值：当γ达到一定程度后，继续缩小γ，对阻塞的改善效果并不显著。

（4）拥堵传播时间波动性的增大会引起拥堵传播速度的明显增加，但其对平衡态阻塞水平影响不大；畅通传播时间波动性的增大会引起拥堵传播速度的小幅增长，但它同时也会减小平衡态的阻塞水平。

现阶段本文研究只是指出了相关参数的含义，对它们的作用规律进行了对比分析，下一步将结合更多实际数据，对这些参数进行定量描述，对拥堵控制策略进行研究。

[1] 吴建军.城市交通网络拓扑结构复杂性研究[D].北京：北京交通大学，2008.

[2] MORENO Y,GÓMEZ J B,PACHECO A F.Instability of Scale-free Networks under Node-breaking Avalanches[J]. Europhysics Letters,2002,58(4):630.

[3] ARROWSMITH D,BERNARDO M D,SORRENTINO F. Effects of Variations of Load Distribution on Network Performance[C]//Conference Proceedings of ISCAS 2005.Kobe:ISCAS,2005:3773-3776.

[4] WU J J,SUN H J,GAO Z Y.Dynamic Urban Traffic Flow Behavior on Scale-free Networks[J].Physica A:Statistical Mechanics&Its Applications,2008,387(2/3):653-660.

[5] WU J J,SUN H J,GAO Z Y.Capacity Assignment Model to Defense Cascading Failures[J].International Journal of Modern Physics C,2012,20(7):991-999.

[6] SUN H J,ZHANG H,WU J J.Correlated Scale-free Network with Community:Modeling and Transportation Dynamics[J].Nonlinear Dynamics,2012,69(4):2097-2104.

[7] ZHENG J F,ZHU Z H,DU H M,et al.Congestion and Efficiency in Complex Traffic Networks[J].International Journal of Modern Physics C,2013,24(10):1633-1637.

[8] QIAN Y S,WANG B B,XUE Y,et al.A Simulation of the Cascading Failure of a Complex Network Model by Considering the Characteristics of Road Traffic Conditions[J].Nonlinear Dynamics,2015,80(1/2):413-420.

[9] 李树彬，吴建军，高自友，等.基于复杂网络的交通拥堵与传播动力学分析[J].物理学报，2011，60（5）：140-148.

[10] 王正武，彭烁，黄中祥，等.城市道路交通网络级联失效的灾害蔓延动力学模型[J].安全与环境学报，2014，14（3）：1-4.

[11] 杨泳，户佐安，严余松.改进型CTM模型突发事件下的拥堵传播规律[J].北京工业大学学报，2015，41（7）：1061-1066.

[12]刘新全.基于贝叶斯网络推理的道路网络级联失效仿真[J].交通运输系统工程与信息，2015，15（2）：210-215.

[13]高自友，吴建军，毛保华，等.交通运输网络复杂性及其相关问题的研究[J].交通运输系统工程与信息，2005，5（2）：79-84.

[14] 何大韧，刘宗华，汪秉宏.复杂系统与复杂网络[M].北京：高等教育出版社，2009.

[15] 张杨，贾建民，黄庆.城市交通中车辆择路行为实证研究[J].管理科学学报，2007，10（5）：78-85.

[16] 邓亚娟，杨云峰，马荣国.基于复杂网络理论的公路网结构特征[J].中国公路学报，2010，23（1）：98-104.

[17] 贾利民，张尊栋，秦勇.城市道路交通网络多模态结构动态性研究[M].北京：科学出版社，2013.

Improved SIS Model of Congestion Propagation of Complex Urban Traffic Network

ZHANG Jun-feng,MA Chang-xi,WU Fang,PU Han,JIA Fu-qiang
(School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China)

In order to deeply analyze the dynamic evolution of urban traffic network congestion,an improved SIS model of traffic congestion propagation was established.The probabilities of an unimpeded node changing to congested one and then recovering unimpeded one were dynamically calculated according to the random factors′influence on it,the conditions and influence abilities of its neighbor nodes and the coupling strength of nodes with different conditions.Moreover,the influence of propagation time of different traffic states on the propagation was considered in this model.Simulated based on BA scalefree network,the evolution of congestion over time was concordant with relevant researches,which verified the effectiveness of this model.The simulation results show that the influence of random factors on initial size of congestion,propagation speed and congestion level at steady state is different according to node properties;the interaction between nodes with different states plays an important role in congestion propagation;the influence of ratio between propagation time of unimpeded state and congestion state exists threshold;the volatilities of propagation time under different states have a certain influence on congestion propagation speed and congestion level of equilibrium state.

BA scale-free network;traffic congestion propagation;improved SIS model;complex urban traffic network;simulation analysis

U491.2

A

2095-9931（2015）06-0020-06

10.16503/j.cnki.2095-9931.2015.06.004

2015-09-12

国家自然科学基金项目（51408288）

张俊锋（1991—），男，陕西凤翔人，硕士研究生，研究方向为交通运输规划与管理。E-mail：jfzhang050@163.com。