基于有限元模型的三维集成电路热分析

杜文雄，唐普英，王舒冰，张思曼

（电子科技大学 光电信息学院，四川 成都 610054）

基于有限元模型的三维集成电路热分析

杜文雄，唐普英，王舒冰，张思曼

（电子科技大学 光电信息学院，四川 成都 610054）

基于有限元理论，对三维集成电路（3D-IC）进行了建模和仿真，研究了不同模型的热分布和计算复杂度。通过Gmsh软件创建3D-IC模型并生成网格化文件。利用Matlab软件提取有限元参数,获到模型的刚度矩阵。用层次矩阵(Hierarchical matrix,H-matrix)表示刚度矩阵，得到了不同模型刚度矩阵的求逆所消耗的存储空间和运算时间。结果表明：随着模型刚度矩阵行列数目的增加，所需要的运算时间和存储空间呈现线性变化关系。

Gmsh；H-matrix；三维集成电路；有限元热分析；刚度矩阵

自1947年第一个半导体晶体管的发明，到1958年采用硅平面工艺的集成电路的诞生，半导体集成电路一直遵循着摩尔定律高速发展。随着集成电路技术的持续发展，在单一芯片上集成更多的资源已面临着重要的挑战。三维集成电路(3D-IC)技术被视为延续摩尔定律的有效技术之一，它可以改善整个集成电路系统的功耗，提高器件的集成度。硅孔道(Through Silicon Via,TSV)是3D-IC中堆叠芯片实现互联的一种新的解决方案。

1)集成电路热分析的意义

一个集成电路实际上是由电学子系统和热学子系统共同组成，两个系统互相耦合：电学元件的功耗作为热学网络的热源，而热学网络中不同温度值作为参数会影响电学系统中元器件及其性能。随着元器件密度，工作速度以及集成电路规模的不断增加，集成电路的能耗密度也越来越大，导致片上温度越来越高。如果不考虑集成电路的热分布问题，电路设计和布局布线就有可能不合理而导致集成电路温度过高以及器件之间温度梯度过大[1]。因此，为保证电路性能和可靠性的要求，有必要在集成电路制造之前对其进行系统的热分析。

2)3 D-IC的优点和技术挑战

3D-IC的优点：①提高封装密度。多层器件重叠结构可成倍提高芯片集成度。②提高电路工作速度。重叠结构使单元连线缩短，并使并行信号处理成为可能，从而实现电路的高速操作。③可实现新型多功能器件及电路系统。

3D-IC面临技术的挑战：①散热问题：由于电路系统拥有了更高的集成度，热功耗也随之提升，表面积与体积比随之下降，传统的平面散热技术不再能满足立体集成电路的散热要求。②测试问题：传统测试技术只针对单层系统，而未提供针对多层芯片集成之后的整体系统测试技术。③制作工艺复杂，成本较高[2-3]。

3)本文的主要工作和意义

国外在3D-IC的热模拟方面已进行了一些研究工作。国内在这方面的报道很少，多是综述性的文章，苏州大学的李文石等人对二维和三维集成电路的热阻进行了计算[4]。胡辉勇等人提出了一种基于 Si和SiGe材料的三维CMOS集成电路,与 Si三维 CMOS结构相比，该电路结构具有明显的速度优势[5]。

本文通过对含TSV的3D-IC进行建模和仿真，研究不同模型的热分布、存储空间复杂度和运算时间复杂度。仿真结果对3D-IC的设计有指导作用。

1 基于有限元理论的热模型

有限元分析是使用有限元方法来分析静态或动态的物理物体或物理系统。在这种方法中一个物体或系统被分解为由有限多个相互联结的、简单、独立的点组成的几何模型。实际的物理模型中推导出来的平衡方程式被使用到每个点上，由此产生了一个方程组。这个方程组可以用线性代数的方法来求解。有限元分析的基本流程：1)节点编号和单元划分。2)计算各单元的单元刚度方程。3)组装各单元刚度方程。4)处理边界条件并求解[6]。

有限元热分析基于能量守恒原理的热平衡方程,用有限元法计算各节点的温度。下面仅介绍系统的温度场不随时间变化的稳态热传递。

传热现象由傅里叶定律决定，即物体的瞬态温度场T(x, y,z,t)应满足以下方程：

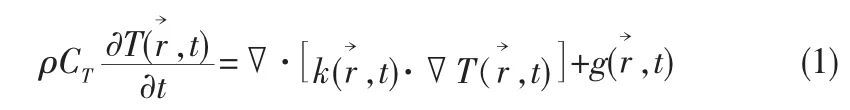
其中ρ为材料密度kg/m3；CT为材料比热(J/(kg·K)）；k是热传导系数（W/(m·K)）；g为物体内部的热量产生率（W/m3）。

考虑方程服从第三类边界条件，即：

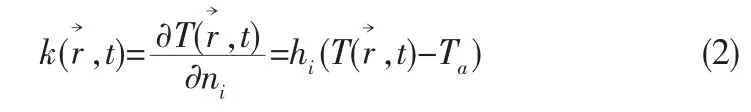
其中ni为边界外法线的方向余弦；hi为物体与周围介质的热交换系数（W/(m2·K)）；Ta为环境温度。对于绝热系统（系统与外界环境无热交换），hi=0。一般情况下，对于不同物质材料和温度，热传导系数k不同。不失一般性，假设对于每一种材料，k是一个常数。因此，(1)式就可以写成：

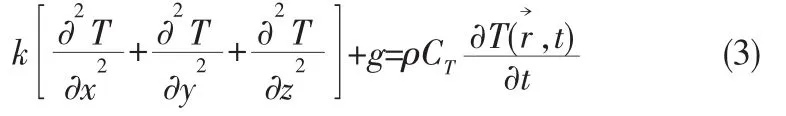
满足下面的边界条件：

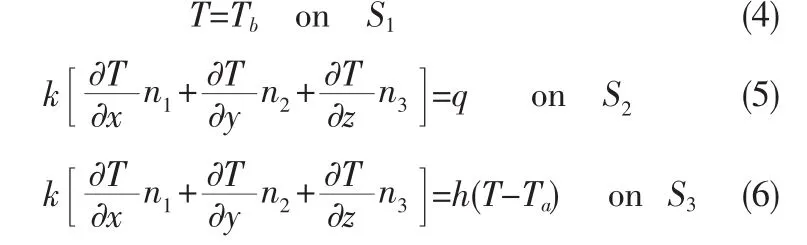
初始温度T=T0，q为在边界S2上的给定热流量，h为物体与周围介质的热交换系数。运用有限元热分析方法求解(3)式。通过在对应节点添加相关数值，可以得到下面方程来表示整个区域。

其中f是整个区域的温度载荷，C是比热矩阵，G是刚度矩阵。考虑稳态问题，即温度不随时间变化。

因此，(7)式可以改写为：

若求出刚度矩阵G的逆矩阵G-1，就可以得到整个模型的热分布T。

2 Gm sh和H-matrix概述

2.1 Gm sh

Gmsh[7]软件是一个带有内置在计算机辅助设计和后期处理器的自动三维有限元网格生成器。Gmsh有4个模块：几何模块，网格化模块，Solver模块，后处理模块。

1)几何模块

Gmsh软件通过边界表示法来描述几何实体。通过定义点、有向曲线、有向曲面、体，自下而上的创建模型。基于这些基础的几何实体可以定义几何实体组。Gmsh软件的程序描述语言允许所有的几何实体通过完整的参数定义来表示。

2)网格化模块

有限单元网格化将给定的模型细分。网格的生成与几何模型的创建一样是自下而上的。首先细分曲线，网格化的曲线被用于网格化曲面，网格化的曲面被用于网格化体。在这个过程中，网格化的实体仅仅被网格化的边界所限制，这样可以保证网格化的一致性。

3)Solver模块

外部解决器可以通过Unix或者传输控制协议及网际协议与Gmsh相连接，允许修改Solver参数，启动外部计算，处理直接从Gmsh后处理模块得到的结果。

4)后处理模块

Gmsh可以加载和操纵多个后处理标量、矢量或张量映射。标量场由等值线（面）或者颜色图表示，而矢量场由三维箭头或者位移图表示。后处理功能包括部分计算,补偿，正面图，边界，组件提取，彩色图，范围修改，动画，矢量图形，输出等。所有后处理选项都可以通过交互界面或者输入脚本文件来存取。脚本文件允许所有后处理操作自动化，用户定义的操作也可以进行后处理。

2.2 H-matrix

H-matrix[8](Hierarchical matrix)，其方法主要目的是使矩阵运算满足线性复杂度。将一个高维的复杂矩阵分层，得到的许多矩阵子集又分解为行列数更低的矩阵，通过模型的几何网格化信息，建立大块的簇树。H-matrix可以没有任何误差地表示刚度矩阵。一个H-matrix H∈CI×I通常与一个可采纳条件相关联，其中I={i1,i2,...,in}包含整个有限元模型的形状函数φi和节点信息。子矩阵Ht×s可以通过因式分解表示为Ht×s≈ABT，其中A是一个t×k矩阵，B是一个s×k矩阵。为了构建合理的H矩阵结构，基于有限元模型几何信息构建的簇树TI×I是必须的。应用大块的簇树构造算法，整体模型的刚度矩阵G就可以没有任何误差地用H-matrix表示。在确定一定精度下，可以用H-matrix表示刚度矩阵的逆矩阵。

3 建模与仿真

本文的建模与仿真是在Intel i5处理器和4 GB内存的仿真环境下进行的。

3.1 Gm sh创建含TSV的三维集成电路模型

通过Gmsh软件创建了含有一个TSV的3D-IC模型（如图1所示）。该模型包括：热沉，集成电路块IC1和IC2，TSV，焊球和衬底。其中TSV实现垂直互联。

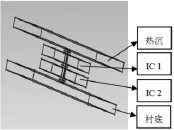
图1 未网格化的3D-IC模型Fig.1 3D-IC model without grids

3.2 M atlab软件提取有限元参数,得到刚度矩阵

由上述基于有限元理论的热模型，利用Matlab软件提取Gmsh建模的有限元参数，得到刚度矩阵。图2是6233行(列)数目的刚度矩阵截图。

图2 6233行（列）数目刚度矩阵Fig.2 Stiffness matrix with line(column)6233

3.3 可视化的三维集成电路模型热分布

设初始温度为T0=300 K，模型的热量分布从300～339 K，其中热源在集成电路块IC2。图3～图5分别表示行（列）数目为4504、5440、6233的刚度矩阵对应模型的热分布图。

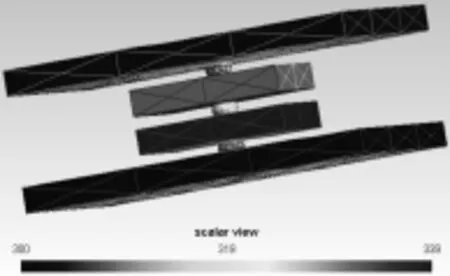
图3 4504行(列)数目刚度矩阵对应模型热分布Fig.3 The thermal distribution of stiffness matrix with line(column) 4504 corresponding to the model

图4 5440行(列)数目刚度矩阵对应模型热分布Fig.4 The thermal distribution of stiffness matrix with line(column) 5440 corresponding to the model

图5 6233行(列)数目刚度矩阵对应模型热分布Fig.5 The thermal distribution of stiffness matrix with line(column) 6233 corresponding to the model

3.4 不同模型刚度矩阵求逆的计算复杂度

对行(列)数较大的矩阵求逆是很耗时的，因此模型的计算复杂度主要体现在刚度矩阵求逆所消耗的存储空间和运算时间。表1列出了不同行(列)数目刚度矩阵求逆耗费的存储空间和运算时间。

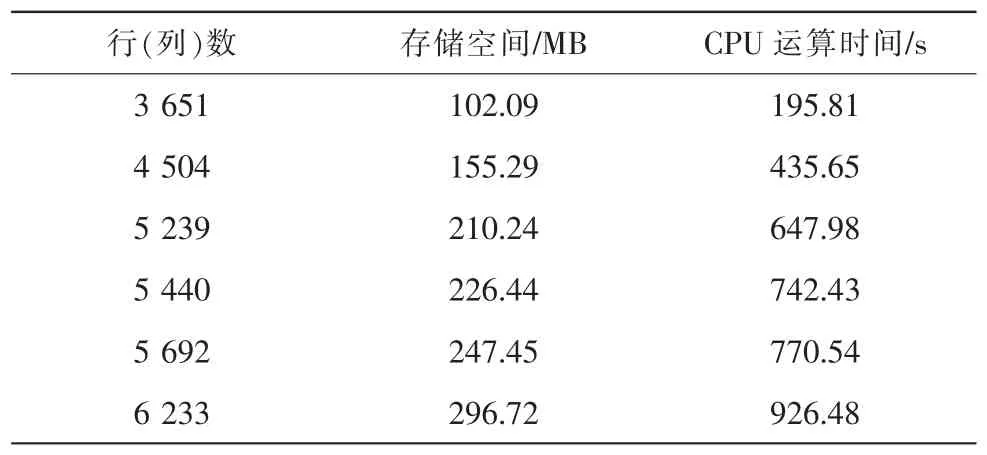
表1 不同模型刚度矩阵求逆耗费的存储空间和运算时间Tab.1 Different model stiffness matrix inversion cost of storage space and computing time

进一步分析表1中的数据，分别用图6和图7表示对应的存储空间复杂度和时间复杂度。

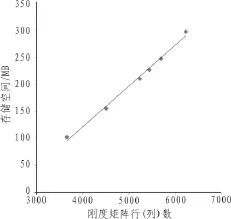
图6 求解刚度矩阵的逆耗费的存储空间Fig.6 To solve the stiffness matrix of the inverse cost of storage space

4 结果分析

对上述仿真结果进行分析，得到以下结论：

1)图3至图5较好地体现了模型的热分布。

2)图6表明：对刚度矩阵求逆所需的存储空间随刚度矩阵行(列)数目的增加呈线性变化关系。

3)图7表明：对刚度矩阵求逆所需的运算时间随刚度矩阵行(列)数目的增加呈线性变化关系。

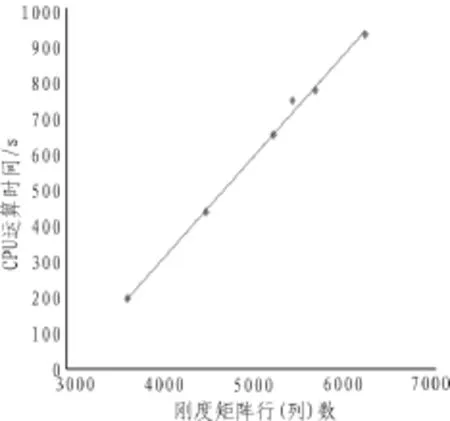
图7 求解刚度矩阵的逆耗费的CPU运算时间Fig.7 To solve the stiffness matrix of the inverse consuming CPU operation time

5 结论

通过Gmsh软件创建三维集成电路模型并生成网格化文件，利用Matlab软件提取有限元参数,得到刚度矩阵，利用层次矩阵(H-matrix)表示刚度矩阵。获得了不同模型的热分布图，得到了不同模型刚度矩阵求逆所消耗的存储空间和运算时间。进一步分析表明，随刚度矩阵行列数目的增加，求对应逆矩阵所需的运算时间和存储空间呈线性变化关系。仿真结果对三维集成电路的设计有指导作用。

[1]王乃龙，刘森，周润德.用有限差分法实现集成电路的电热耦合模拟[J].微电子学，2004,34(3):295-297.WANG Nai-long,LIU Miao,ZHOU Run-de.Electro-Thermal simulation of integrated circuits using finite difference method[J].Microelectronics，2004,34(3):295-297.

[2]王凤娟，朱樟明，王宁，等.考虑硅通孔的三维集成电路最高层温度模型[J].计算物理，2012(4)：109-113.WANG Feng-juan，ZHU Zhang-ming，WANG Ning，et al.A thermal model for top layer of three-dimensional integrated circuits with through silicon via[J].Chinese Journal of Computational Physics，2012(4)：109-113.

[3]杜秀云，唐祯安.三维集成电路工作热载荷工况的有限元仿真[J].系统仿真学报，2012(2)：49-52.DU Xiu-yun,TANG Zhen-an.Finite element simulation for 3D-IC of working process under thermal loads[J].Journal of System Simulation，2012(2)：49-52.

[4]李文石.二维和三维集成电路的热阻计算 [J].微电子学，2005(5):40-43.LI Wen-shi.Computation of thermal resistance for 2D-and 3D-IC’s[J].Microelectronics，2005(5):40-43.

[5]胡辉勇，张鹤鸣，贾新章，等.Si-SiGe材料三维CMOS集成电路技术研究[J].半导体学报，2007(5):49-53.HU Hui-yong,ZHANG He-ming,JIA Xin-zhang,et al.Study on Si-SiGe three-dimensional CMOS integrated circuits[J].Chinese Journal of Semiconductors，2007(5):49-53.

[6]曾攀.有限元分析基础教程[M].北京：清华大学出版社，2008.

[7]Geuzaine C,Jean-Francois Remacle.Gmsh:a three-dimensional finite element mesh generator[J].International Journal for Numerical Methods in Engineering,2009,79(11)：1309-1331.

[8]Mario Bebendorf.Hierarchical Matrices[M].Germany:Springer, 2008.

3D-IC thermal analysis based on the finite element model

DU Wen-xiong,TANG Pu-ying,WANG Shu-bing,ZHANG Si-man
（School of Optoelectronic Information,University of Electronic Science and Technology of China,Chengdu 610054,China）

Three-dimensional integrated circuit(3D-IC)was modeled and simulated based on the finite element model.The thermal distribution and the computation complexity for different model were studied.The 3D-IC models were created and the mesh files were generated by Gmsh.The finite element parameters were extracted and the stiffness matrices were obtained using Matlab.The stiffness matrix was represented by the hierarchical matrix(H-matrix).The storage space and computing time in?solving inverse matrix of stiffness matrix were generated for different model.The results show that the computation time and the storage space for solving different complexity of 3D-IC model present linear relationship as the increase of the number of the stiffness matrix ranks.

Gmsh;H-matrix;3D-IC;finite element thermal analysis;stiffness matrix

TN407

A

1674－6236（2015）10-0079-04

2014-09-24 稿件编号：201409210

杜文雄(1993—)，男，四川广安人。研究方向：电子技术。