关于NA随机序列的一类强极限定理

屈红红 范爱华

(安徽工业大学数理科学与工程学院，安徽 马鞍山 243002）

关于NA随机序列的一类强极限定理

屈红红 范爱华

(安徽工业大学数理科学与工程学院，安徽 马鞍山 243002）

主要考虑同分布的NA随机序列(ξ，ξn）n∈N，满足或。通过把划分成四部分，得到一类强极限定理。

NA随机序列；三级数定理；大数定律

1 引言

设(ξ，ξn）n∈N是i.i.d随机变量，满足Eξ=0或。众所周知，对于任意一个常量(bn）n∈N，不成立[1-2](cf.Chowet al.(1961），Maller(1978），Adler(1989）.

近来Andre Adler(2001，2002）考虑了以下强大定律的形式：

这里的(an，bn）n∈N是常量。这些强大定律被看作精确强大数定律。因为Andre Adler(2001，2002）在文中指出，存在一个几乎肯定非零极限，即使随机变量为零，或不存在[3-4]。

对于NA随机序列来说，通过Andre Adler(2001，2002），在本文中我们考虑了NA随机变量，并建立了一类极限定理。

定义1 如果对于｛1，2，…，n }不相交子集A和B的每部分，随机变量的一有限集合ξ1，ξ2，…，ξn被认为是NA，如果

当f和g是逐渐增加且导致协方差存在。如果每个有限子集合是NA，那么随机变量的一组有限集合｛ξt，t∈T}是NA。

这个定义由Alam and Saxena(1981）提出且由Joag-Dev和Proschan(1983）[5-6]仔细研究。同样地Joag-Dev和Proschan(1983）[8-9]指出并证明，许多著名的多变量的分布过程NA性质，比如(a）多项式，(b）不同多项式的卷积，(c）多元的超几何，(d）Dirichlet，(e）Dirichlet复合多项式，(f）负相关的正态分布，(g）排列分布，(h）不重复的随机抽样，并且(i）排列的联合分布。由于它在多元统计分析和可靠性的广泛应用中，最近NA概念已经得到了相当大的关注。对于更多的信息我们参考Han-Ying Liang(2000）[7]并引用其中。

引理1[10](Su Chun et al.1998）设(ξn）n∈N是NA随机变量的一个序列。如果，对于某个d＞0，因此

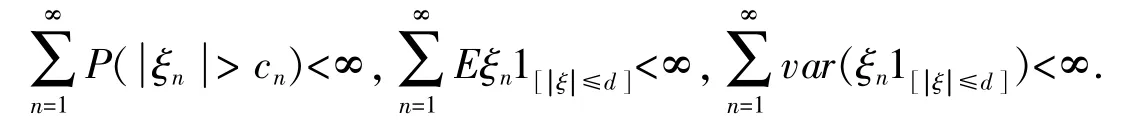
则

引理2[10](Su Chun et al.1998）设(ξn）n∈N是NA和fn不减少的Borel函数一列，然后(fn(ξn））n∈N也是NA。

2 主要的结果

我们首先考虑Eξ=0的情况。在这种情况下，我们首先给出下面的定义。

定义2 设ξ是一个随机变量有Eξ=0，我们称

作为缩短的一阶矩。

因为在Andrre Adler(2002），我们定义c作为对称性的参数，其中

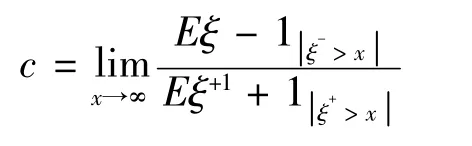
定理1 设(ξ，ξn）n∈N是同分布的NA随机变量，有Eξ=0和，其中L(x）是缓慢的变化。设(an）n∈N和(bn）n∈N是那些如上定义的常量。如果

则有

其中b＞0.

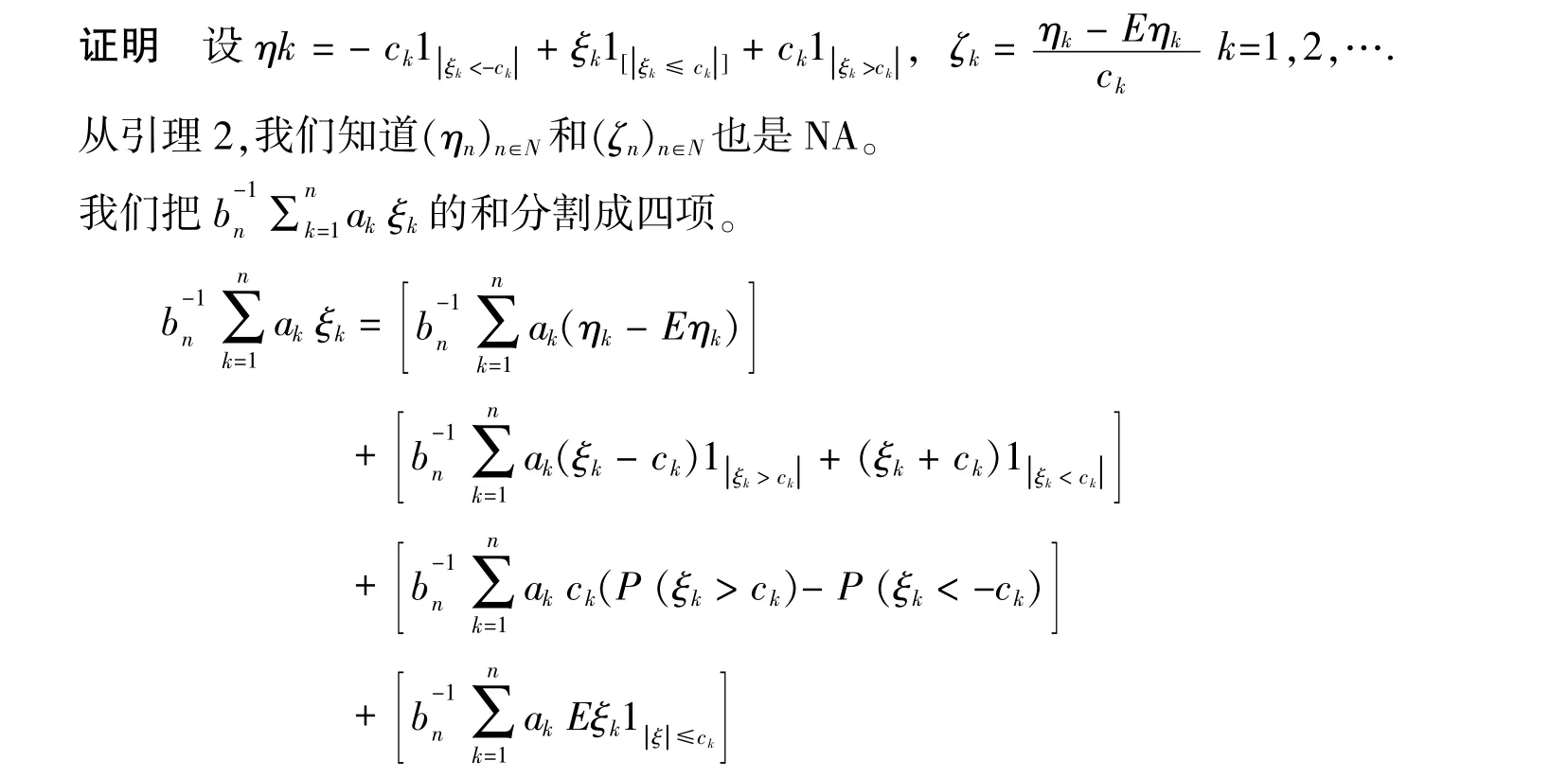
定理2 设ξ，(ξn）n∈N，是同分布的NA随机变量。有，这里L(x）是缓慢变化的，且(2.1）保留，然后

[1]Adler，A.Exact sequences for sums of independent random variables[J].Proceedings of theInternational Conference on Almost Everywhere Convergence in Probability and Ergodic Theory，Boston Academic Press∶11-29.

[2]Alam，K.&Saxena，K.M.L.Positive dependence in multivariate distributions[J].Comm.Statist.Theory Methods，1981，（A10）∶1183-1196.

[3]Andr′e Adler.Exact laws for multidimensionally indexed random variables[J].Journal of Multivariate Analysis.2001，（77）∶73-83.

[4]Andr′e Adler.Laws of large numbers for the maximal order statistics from a triangulararray[J].Bulletin of the Institute of Mathematics Academia Sinica，2002，（4）∶239-251.

[5]Block，H.W.&Savits，T.H.Some concepts of negative dependence[J].Ann.Probab.1982，（10）：765-772.

[6]Chow，Y.S.&Robbins，H.On sums of independent random variables with infinitemoments and“fair”games[J].Proc.Nat.Acad.Sci.U.S.A.，1961，（47）∶330-335.

[7]Hanying，L.Complete convergence for weighted sums of negatively associated random variables[J].Statistics&Probability Letters.，2000，（48）∶317-325.

[8]Maller，R.A.Relative stability and the strong law of large numbers[J].Z.Wahrsch.verw.Gebiete，1978，（43）∶141-148.

[9]Joag-Dev，K.&Proschan，F.Negatively associated random variables with applications[J].Ann.Statist，1983，（11）∶286-295.

[10]苏淳，王岳宝.同分布NA序列的强收敛性[J].应用概率统计，1998，（2）∶131-140.

ON A CLASS OF STRONG LIMIT THEOREMS ON NEGATIVELY ASSOCIATED RANDOM VARIABLES

QU Hong-hong FAN Ai-hua
（School of Mathematics，Physics Science and Engineering，Anhui University of Technology，Ma'anshan Anhui 243002）

In this paper，the identically distributed NA random variables(ξ，ξn）n∈Nwhich are in accordance withorare taken into account.By dividinginto four parts，a class of strong limit theorems is obtained.

NA random variables；three-level mathematical theorem；law of large numbers

O211.4

A

1672-2868（2015）06-0010-04

责任编辑：陈 侃

2015-10-24

安徽工业大学研究生创新基金(项目编号：2015130）

屈红红(1983-），女，陕西咸阳人。安徽工业大学数理科学与工程学院，硕士研究生。研究方向：概率论与极限理论。