基于OpenFOAM的熔融池自然对流传热与凝固数值研究

王 溪，孟召灿，程 旭（国核（北京）科学技术研究院有限公司，北京 100029）

基于OpenFOAM的熔融池自然对流传热
与凝固数值研究

王 溪，孟召灿，程 旭
（国核（北京）科学技术研究院有限公司，北京 100029）

摘要：熔融物堆内滞留是第3代核电技术重要的严重事故缓解措施之一，堆芯熔融池在压力容器下封头壁面的热流密度分布直接影响该策略的有效性。本文基于开源的数值计算流体力学软件平台Open－FOAM，应用相变模型和浮升力模型二次开发了用于模拟堆芯熔融物由内热源或温差驱动的自然对流传热与相变求解器。应用该求解器模拟了瑞典皇家理工学院开展的二维氧化池与金属层耦合传热试验，获得了氧化池和金属层硬壳的相场，以及熔融池内的温度分布及沿容器壁面的热流密度分布。计算结果表明，该模型可用于熔融物凝固与自然对流的模拟，为深入分析核电厂采用熔融物堆内滞留措施后熔融池的行为奠定了基础。

关键词：严重事故；CFD；熔融物堆内滞留；凝固；自然对流

通过压力容器外部冷却滞留堆芯熔融物（IVR－ERVC）是第3代核电技术重要的严重事故缓解措施之一，已应用于AP1000、CAP1400等堆型。该措施是在严重事故下，使用冷却剂淹没压力容器，熔化后的堆芯重定位到压力容器下封头内，衰变热通过熔融池自然对流和顶部辐射传递给压力容器，最终通过压力容器壁的导热传递给外部冷却剂［1］。

美国核管理委员会和西屋公司在AP600／1000的研究中，结合ACOPO、UCLA和MELAD等试验提出的经验关系式，采用了集总参数法分析两层熔池的热流密度分配，评价了IVR的有效性［2］。德国卡尔斯鲁厄理工大学（KIT）完成了以熔盐为模拟材料1∶5比例三维LIVE试验，重点研究熔融物进入下封头的瞬态热冲击［3］。瑞典皇家工学院（KTH）完成了以熔盐为模拟材料1∶8比例二维切片熔融池金属层和氧化层耦合相变传热SIMECO试验，机理上深入探索了熔融池传热行为，并采用了相变等效传热模型（PECM）模拟了SIMECO试验，但该方法不能用于分析熔融池的流场［4］。在韩国的APR1400熔融物堆内滞留的研究中，韩国原子能研究院等采用CFD程序LILAC模拟了氧化池和金属层的传热，计算中假设氧化池熔融物与硬壳的交界面、金属层与未熔化的压力容器壁的交界面，以及金属层上表面均为等温壁面边界条件，仅模拟了熔融池内液相区域的流动和传热［5］。本文基于开源计算流体力学平台OpenFOAM，将用于模拟凝固相变的Enthalpy－porosity模型和浮升力Buoyancy模型应用到该软件中，并应用该软件模拟KTH所开展的基于模拟材料的二维氧化池和金属层耦合传热试验，以初步验证该数值模型在准稳态熔池传热研究方面的可用性。

1　凝固相变数值模型

1．1 基本控制方程

针对熔融物在压力容器下封头内的流动和相变问题，在假设堆芯熔融物为不可压缩流体的情况下，可建立以下方程。

连续性方程：

Δ·U＝0（1）

其中，U为流体速度矢量。

动量方程：

Sb＝－ρgβmax［T－Tl，0］（3）

其中：t为时间；μeff为有效黏性系数；p为压力；ρ为密度；g为重力加速度；β为热膨胀系数；T为流体温度；Tl为液相线温度。动量方程包括两个源项：Sb为浮升力项，当温度大于液相线温度时，将温度与液相线温度的差值乘以材料的热膨胀系数、密度和重力加速度，作为材料的浮升力，方向与重力方向相反，当温度小于液相线温度时，认为浮升力消失；Sm为描述介于固相与液相之间的固液两相过渡区域类似于一种多孔介质对流动产生的阻力，称为Darcy项。

能量方程：

其中：h为焓；λeff为有效导热系数；能量方程的源项是体积内热源Q，用于模拟衰变热。

1．2 Enthalpy－porosity模型

Enthalpy－porosity模型是工程上应用最为成熟的凝固模型，该模型由Voller等［6］提出。在该模型中，动量方程Darcy项由Darcy定律［7］推导而来，Darcy定律方程如下：

其中：K为渗透率；μ为流体的黏度；Δp为压力梯度。Darcy定律描述了流体以一定速度流过多孔介质所产生的压力下降，或说是阻力。

Darcy方程中的K由Carmen－Kozeny方程获得［8］，假设多孔介质由若干圆孔通道组成，细孔的半径为r，空隙体积比为φ，多孔介质的长度为L，通道平均实际长度为La，则K为：

K＝φr2L／8La（6）

如果定义单位体积多孔介质内空隙的表面积为Spv，则K为：

K＝φL／2S2pvLa（7）

Spv＝S／Vp（8）

假设固液两相过渡区域中凝固的固相材料晶体为等直径的圆球形颗粒状，熔融的液相的材料在这些固相颗粒之间流动，液相的体积份额即为该多孔介质的空隙体积比φ。单位体积内固液相接触的表面积为：

将式（9）代入式（7），可得固液两相过渡区域的K为：

将式（10）代入式（6）可得液相速度与多孔介质压降的关系：

式（11）变形可得：

式（12）的表达为压力梯度，这与动量方程中的压力项相当，因此可直接得到动量方程的Darcy源项表达式为：

其中：dp为固相颗粒的平均直径；ε为一极小数，防止除零；C为系数的整合。不难看出，Darcy项在动量方程中为一与速度呈正比的阻力项，且与液相体积份额相关。实际使用中C的取值越大，则计算结果的固液交界区域越薄，相反则越弥散。对于C的选取，需通过真实材料的试验获得。本文参考文献［6］，选取C＝1．6×103kg／（s·m－3）进行计算。

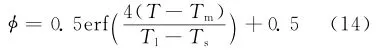
其中：erf为误差函数；Ts为固相线温度；Tm为固液相线温度的平均值。流体的温度在固液相线温度之间，随温度的升高，φ增大。温度高于液相线温度时，φ＝1；温度低于固相线温度时，φ＝0。

能量方程中的焓h与材料的温度和液相体积份额相关，如式（15）所示。

h＝cpT＋L（15）

将式（15）代入式（4），可得式（16）。

方程右端多出了一个由相变引起的潜热的释放和吸收的源项，如式（17）所示。

将式（14）代入式（17），可得：

上式可认为是关于温度T的能量方程右端的另外一个由相变引起的源项，由于引入了误差函数，液相体积份额对时间和空间上的一阶导数具有连续性。

以上控制方程考虑了相变、浮升力和内热源的作用，将这些方程应用于OpenFOAM平台，可求解凝固相变条件下的内热源驱动自然对流传热。

2　数值模型验证

2．1 SIMECO试验

SIMECO是KTH所开展的针对熔池传热研究的二维半圆形切片试验装置（图1）。该试验包括了氧化池和金属层耦合传热试验，可用于研究氧化池和金属层硬壳界面对传热的影响，初步探索金属层热聚焦效应［10］。

图1　 SIMECO试验装置示意图［10］Fig．1 Scheme of SIMECO experiment setup［10］

如图1所示，该试验装置包括1个半圆形切片铜制试验段，其直径为62．0cm，高度为53．0cm，厚度为9．0cm。该试验段的尺寸最高可达到的瑞利数Ra的范围为1012～1013。试验容器壁厚为2．3cm，由冷却回路进行冷却，该回路分为两部分：一部分用于冷却试验容器的顶盖，另一部分用于冷却试验容器的底部，冷却系统主要是为试验段提供定温边界条件。模拟试验段内热源的加热系统为1根直径为3mm、长为4m的电阻加热丝，最高可达4kW的加热功率。

KTH在该装置上开展了研究氧化池和金属层自然对流传热模化试验，包括采用50%NaNO3－50%KNO3作为模拟材料的熔池试验、用铜板将模拟材料水分隔的分层传热试验、石蜡和水的分层传热试验、较高熔点的硝酸盐与Cerrobend合金的分层试验以及甘油和Cerrobend合金的无硬壳界面耦合试验等。

选取SIMECO系列试验中的硝酸盐和Cerrobend合金耦合相变传热试验，开展了CFD模拟和模型验证。该试验采用NaNO3－KNO3混合物作为氧化池的模拟材料，采用低熔点Cerrobend合金（由铅、铋、锡和镉等材料按一定比例混合而成）作为金属层的模拟材料。模拟材料的物性列于表1。

表1　 模拟材料NaNO3－KNO3和Cerrobend合金物性Table 1 Material properties of NaNO3－KNO3and Cerrobend alloy

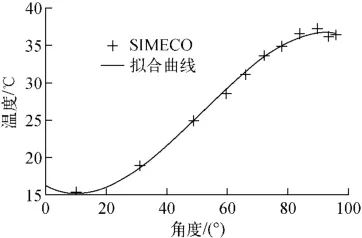
图2　 SIMECO试验容器内壁温度分布拟合Fig．2 Interpolation of vessel inner wall temperature distribution of SIMECO experiment

该试验金属层和氧化池是由1层薄铜板完全分隔开，由于铜板的传热性能很好，可忽略其热阻。上部的金属层无内热源，氧化池和金属层由铜板耦合传热。试验段金属层和氧化池的高度比分为两种：3∶27和6∶27。试验中金属层顶部的边界条件采用了4种不同的边界，包括顶部温度为6、40、86℃定温边界条件和顶部绝热边界条件，分别研究较厚金属层硬壳、较薄金属层硬壳和无顶部硬壳的情况。共开展了14组试验，本文选取了9号试验开展数值模拟和模型验证，工况和边界条件为：输入功率，2kW；顶部温度，40℃；侧面温度，6℃；金属层厚度，6cm。SIMECO试验容器底部温度分布拟合如图2所示，作为CFD模型的输入底部壁面边界条件。其中，0°表示容器底部的温度，90°表示容器横向赤道位置的温度。

图3　 SIMECO 9号试验数值模型Fig．3 Numerical model of SIMECO No．9experiment

2．2 SIMECO试验数值模拟

结合上面给出的初始条件和边界条件，本文应用基于OpenFOAM二次开发的CFD求解器对SIMECO 9号试验进行了数值模拟，数值模型如图3所示。氧化池的电阻丝加热等效为体积内热源，自然对流的作用下将热量传递给上方的金属层和底部的圆弧形容器壁面；金属层底部获得氧化池传递的热量等效为定热流密度边界条件，在对流的作用下将这一部分热流传递给顶部和侧壁面。本文依据文献［5］对于自然对流换热系数网格相关性的分析结论，选取网格分辨率为800。计算采用了Spallart－Allmaras湍流模型。由于自然对流属于准稳态流动，首先基于稳态SIMPLE算法获得一初步的稳态结果，然后将计算结果作为初始条件，采用瞬态PIMPLE算法获得一满足能量平衡的准稳态结果。

9号试验的数值模拟速度场如图4所示。图中流场分隔为流体区域和固相区域，靠近冷却壁面的是固相区域，流体区域内的箭头是速度矢量。金属层在下方氧化池的传热作用下，形成了类似于Bernard对流的流型，无数个小漩涡将热量传递给顶部和侧面未熔化的区域。由于金属层侧面得到了有效冷却，硬壳形成的形状为中间区域薄，靠近金属层侧壁位置较厚。受金属层自然对流漩涡的影响，硬壳与熔融物交界面为波浪形起伏。从氧化池的速度场和液相体积份额分布可看出，氧化池上壁面的硬壳很薄，这是由较高的热流密度引起的，沿着径向方向，氧化池顶部的硬壳厚度较为均匀，这说明了氧化池向上传递的热流密度分布相对均匀。氧化池半圆弧形壁面的硬壳越靠近底部区域越厚，这是由氧化池向容器壁传热的热流密度分布引起的，底部的流体温度较低，同时热流密度也较低；熔池靠近半圆形弧面上方的位置，由于以温度差引起的自然对流换热为主，热流密度较高，因此硬壳的厚度较薄。从氧化池的流场可看出，在氧化池上半部分空间区域内形成了明显的大漩涡，这些漩涡不断地将内热源产生的热量传递给顶部和底部壁面，然后通过硬壳的导热载出热量。CFD计算的结果直观呈现出熔池内硬壳几何形状以及熔融物的流动行为。

图4　 SIMECO 9号试验数值模拟速度场Fig．4 Velocity field of numerical simulation for SIMECO No．9experiment

图5为SIMECO 9号试验的数值模拟温度场。从金属层温度场可看出，在两个漩涡的中间均形成一股热流，将从底部获得的热量传递给未熔化的金属层材料，受到冷却后下降。金属层的硬壳区域的温度梯度明显高于下半部分对流区，因为对流换热速率远高于导热速率。从氧化池的温度场可看出，上半部分在大漩涡的作用下，温度分布非常均匀，而下半部分出现了明显的热分层现象，越靠近底部温度越低，底部硬壳区域的温度梯度较明显。

图5　 SIMECO 9号试验数值模拟温度场Fig．5 Temperature field of numerical simulation for SIMECO No．9experiment

图6为SIMECO 9号试验测量获得的中心线温度分布与CFD数值模拟结果的比较。从图中可看出，由于氧化池底部硬壳热阻较大，温度上升较为迅速，进入熔融氧化池区域，温度变化较小，即熔池内熔融区域的温度分布较为均匀。氧化池到金属层交界的区域，温度在硬壳和两个流动边界层的影响下，出现一阶跃下降，因这个硬壳分界面和上下两个边界层起到了热阻的作用。金属层的熔融区域温度分布梯度较小，到了金属层的凝固硬壳区域，出现了较为明显的温度下降，这是由于导热速率相对于对流换热速率很低。

图6　 SIMECO 9号试验中心线温度分布与CFD结果比较Fig．6 Temperature distribution along center line of SIMECO No．9experiment compared with CFD result

图7为SIMECO 9号试验测量获得的热流密度分布与CFD模拟结果的比较。可看出，目前CFD获得的结果明显高于试验结果，说明了模拟获得的热流密度分布相对试验结果存在一定误差。在CFD结果中，95°位置附近热流密度分布有一峰值，这是由金属层底部等效为均匀热流边界和金属层的高热导率引起的。总体上，CFD技术在准确预测两层熔池热流密度上存在一定误差，但趋势符合较好。

图7　 SIMECO 9号试验热流密度分布与CFD结果比较Fig．7 Heat flux distribution of SIMECO No．9 experiment compared with CFD result

3　结论

本文将Enthalpy－porosity模型应用于OpenFOAM平台，分析了KTH开展的二维模拟材料氧化池和金属层耦合传热试验，研究了内热源驱动和温差驱动湍流自然对流传热与凝固现象。计算获得了液相熔融物和硬壳的分布，以及温度和热流密度分布，与试验数据对比表明，该数值模型可初步适用于熔融池传热和相变研究，为研究IVR条件下堆芯熔融池的行为特性提供了参考。

参考文献：

［1］ SEHGAL B R，THEERTHAN A，GIRI A，et al．Assessment of reactor vessel integrity（ARVI）［J］．Nucl Eng Des，2003，221：23－53．

［2］ ESMAILI H，KHATIB RAHBAR M，BASU S，et al．Analysis of in－vessel retention and exvessel fuel coolant interaction for AP1000［R］．Washington D．C．：U．S．NRC，2004．

［3］ KRETZSCHMAR F，FLUHRER B．Behavior of the melt pool in the lower plenum of the reactor pressure vessel－review of experimental programs and background of the LIVE program［R］．Germany：Karlsruhe Institute of Technology，2008．

［4］ CHI T T．The effective connectivity model for simulation and analysis of melt pool heat transfer in a light water reactor pressure vessel lower head［D］．Sweden：Royal Institute of Technology，2009．

［5］ REMPE J L．In－vessel retention strategy for high power reactors［R］．Idaho：Idaho National Engineering and Environmental Laboratory，2005．

［6］ VOLLER V R，PRAKASH C．A fixed－grid numerical modeling methodology for convection－diffusion mushy region phase－change problems［J］．Heat Mass Transfer，1987，30：1 709－1 720．

［7］ DARCY H．Les fontaines publiques de la ville de dijon［R］．Paris：Victor Dalmont，1856．

［8］ CARMAN P C．Fluid flow through granular beds［R］．London：Institution of Chemical Engineers，1937．

［9］ RÖSLER F，BRÜGGEMANN D．Shell－and－tube type latent heat thermal energy storage：Numerical analysis and comparison with experiments［J］．Heat and Mass Transfer，2011，47（8）：1 027－1 033．

［10］ASKAR A G．Natural convection heat transfer in two－fluid stratified pools with internal heat sources［D］．Sweden：Royal Institute of Technology，2002．

Numerical Investigation on Natural Convection and
Solidification of Molten Pool with OpenFOAM

WANG Xi，MENG Zhao－can，CHENG Xu
（State Nuclear Power Research Institute，Beijing100029，China）

Abstract：The in－vessel retention is adopted by the third generation nuclear power technology as an important severe accident mitigation strategy．The integrity of reactor pressure vessel depends on the heat flux distribution of molten pool．In present study，the solidification model in open source CFD software OpenFOAM was applied to simulate solidification and natural convection which was driven by internal heat source or temperature difference．The stratified molten pool heat transfer experiment carried out by Royal Institute of Technology was analyzed in the paper，and the solidified crust，temperature and heat flux distributions were obtained．The simulation results were compared with experimental data．It is shown that this numerical method can be used in the simulation of natural convection and solidification of molten pool，and it will probably be used in the analysis of molten corium behavior in reactor lower head．

Key words：severe accident；CFD；in－vessel retention；solidification；natural convection

作者简介：王 溪（1985—），男，山东成武人，助理工程师，硕士，核能科学与工程专业

收稿日期：2014－04－22；修回日期：2014－06－09

doi：10．7538／yzk．2015．49．08．1393

文章编号：1000－6931（2015）08－1393－06

文献标志码：A

中图分类号：TL33