液体多模态晃动充液航天器姿态机动复合控制

宋晓娟，岳宝增，闫玉龙，邓明乐

(北京理工大学宇航学院，北京100081)

0 引言

为了完成长时间复杂的航天任务，航天器需要携带大量的发动机液体燃料。液体燃料晃动质量的增加使得液体晃动更容易与航天器的姿态运动及柔性附件振动发生耦合从而影响航天器的稳定性，甚至可能导致航天器飞行任务失败。开展相关研究的紧迫性和重要性还可以从美国航空航天管理局于2010年2月所发射的太阳动力学高精度观测卫星的研制过程和在轨运行经历而窥见一斑。SDO观测器含有2个大型燃料贮腔(充液重为1400 kg，占卫星总重的47%)。在观测器执行第二次远地点主发动机点火并进行变轨机动过程中，控制系统发出了过载警告信号，同时迫使观测器关闭主发动机并转入安全模式。科研人员在长达一周的时间内进行了13次轨道和姿态机动并最终成功地将太阳动力学观测器引导到预定的使命轨道。相关工程技术人员在总结这次事故经验教训中得到两点非常重要的启示:其一是传统的液体晃动等效力学模型并不能有效模拟液体非线性晃动动力学(尤其是远地点发动机点火阶段);其二是在充液复杂航天器的研制过程中，必须考虑液体晃动及控制系统之间的非线性耦合动力学问题［1］。对于大型充液航天器而言，液体非线性等效力学模型的建立［2－3］、流固耦合非线性系统的稳定性及分叉［4－5］、液体晃动抑制［6］以及相应现代控制理论等问题的研究仍是有待解决的关键性课题［7］。

目前有关充液航天器刚－液－控－耦合动力学研究的文献报道中，大部分工作只涉及液体晃动的基阶模态，即只考虑单一质量摆模型和单一质量弹簧模型，而忽略了高阶模态。虽然高阶模态的晃动幅值很小，但在建立耦合系统更精确模型时应适当增加模态的阶数。有文献报道，如果在耦合系统建模时加入前两阶或前三阶模态将能更加准确地反映液体晃动动力学特征［8］。

近年来，一些学者将输入成型技术应用于液体晃动抑制中取得了令人瞩目的成果。文献［9］通过数值模拟和实验证明鲁棒输入成型器在一定参数范围内可以有效抑制储液箱内液体残余晃动;文献［10］采用输入成型控制技术详细研究了球形贮箱的液体晃动的抑制问题;文献［11］将前馈输入成型技术与动态逆方法相结合，对充液航天器轨道转移过程中的大角度姿态机动问题进行了复合控制方法的研究。

对于现代大型航天器的控制设计不可避免地会遇到各种扰动(诸如太阳光压、重力梯度)和不确定参数问题(诸如柔性附件振动及液体晃动等)。这就要求控制系统具有很强的自适应与鲁棒性［9－11］。研究表明，采用自适应动态输出反馈控制策略可以达到对复杂航天器的良好控制效果［12］。

本文对充液航天器采用零动量反作用轮进行三轴姿态稳定，其在航天器的3个主惯性轴上各装一个动量轮，3个动量轮相互正交(如图1所示)，应用动量矩守恒定理建立航天器系统姿态动力学方程和弹簧质量等效力学模型的前两阶模态液体晃动动力学方程。针对充液航天器大角度姿态机动问题设计了基于自适应动态输出反馈控制器及多模态前馈输入成型技术的复合控制器，并进行了数值仿真试验研究。

1 充液航天器动力学建模

1. 1 姿态动力学方程描述

假设旋转坐标系对惯性系有一个旋转角速度ω，航天器系统在惯性坐标系下的总动量p可表示为

式中:f为系统外力。系统在惯性系中的动量矩h有以下关系式

式中:v为系统平动速度，g为外力矩。反对称矩阵

1. 2 建立航天器数学模型

带有单个储液腔体的充液航天器模型如图1所示，假设航天器本体坐标系的原点与系统质心重合，航天器本体为刚体，提供控制力矩的动量轮分别作用在三个坐标轴上，储液腔体中的晃动燃料等效为二阶弹簧质量模型如图2所示。图中的各个参数物理意义如下:O为航天器质心，OXYZ为与刚体航天器固连的参考坐标系，假设航天器的椭球形燃料贮箱部分充液且整个系统处于零重力环境，将液体晃动等效为弹簧质量模型并考虑其二阶模态振动，一阶晃动模型参数为mf1，kf1，cf1，其沿着OZ轴方向距离质心O的距离为bf1，二阶晃动模型参数为mf2，kf2，cf2，bf2，不参与晃动液体参数 If0，mf0，bf0。动量轮关于坐标轴是轴对称的，其到质心的距离为bw，其转动惯量为Is。

航天器质心到一阶晃动质量mf1的距离为rOf1vO+ω×rOf1+˙η1，η1为一阶弹簧质量的晃动位移。这里，η1= ［η11η12］T，η11为晃动质量沿着 OX 轴的晃动位移，η12为晃动质量沿着OY轴的晃动位移。同理可知，二阶晃动质量mf2的位移及速度表达式。由于研究液体小幅晃动，略去速度项中的二阶高次项，则

在转动坐标系中，晃动质量的动量为

由于本文只讨论姿态转动对航天器的影响，没有考虑平动的影响，所以认为v0=0，并且应用式(1)，得到关于等效液体晃动质量的动力学方程

图1 充液航天器系统动力学模型Fig.1 Simplified model of the liquid-filled spacecraft

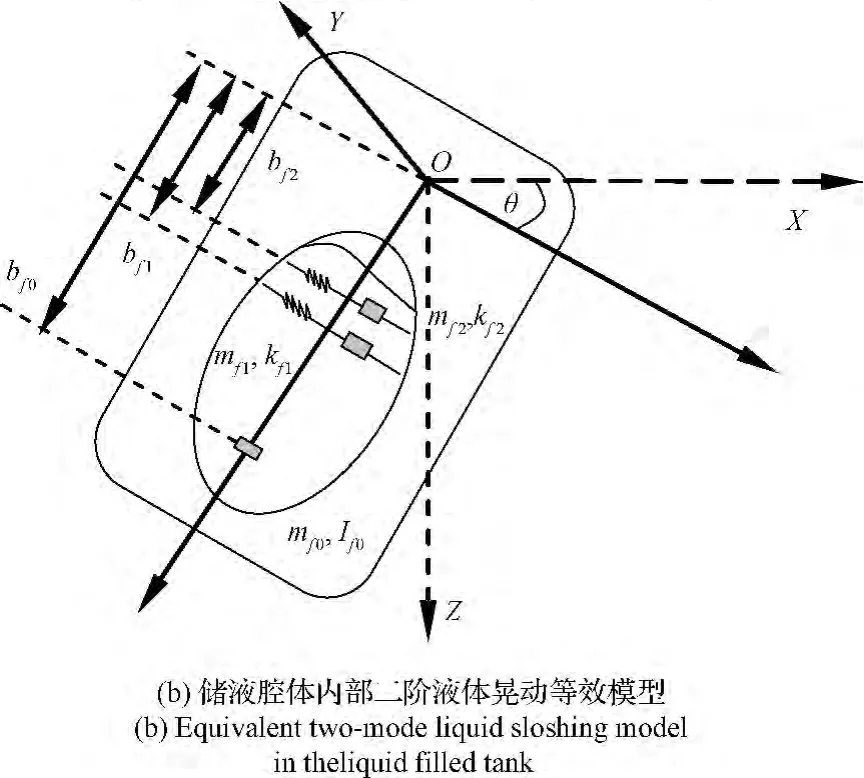
图2 航天器液体贮箱内部结构图Fig.2 The internal structure diagram for the liquid filled tank of spacecraft

转动坐标系中，航天器整体的动量矩为

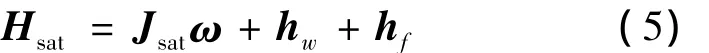
结合式(5)及式(2)，可以得到带有动量轮的充液航天器的动力学方程为

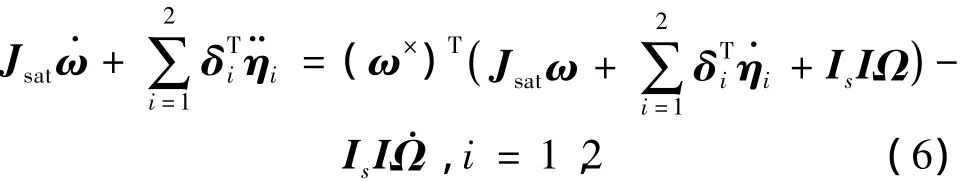
由此，得到充液航天器系统的动力学方程。

2 大角度反馈控制率设计

2. 1 设计自适应动态输出反馈姿态控制器

将动力学方程(6)、(4)写成矩阵形式，液体为小幅晃动，省略式(4)中的高阶小量。为了控制系统方便引入了一个新的变量α。控制系统为

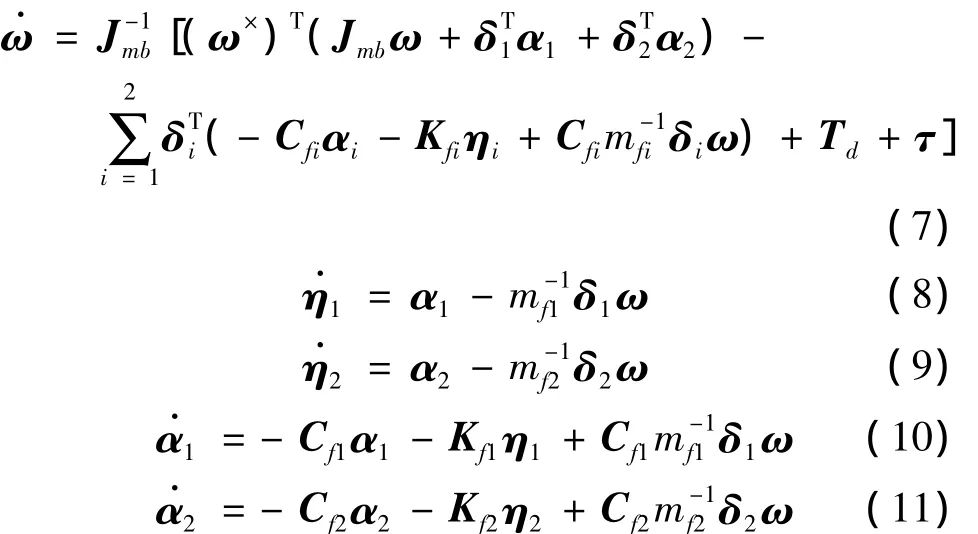
用四元数描述动力学方程

式中:q=［q1q2q3］T，qTq+q20=1。

设计控制器τ确保闭环系统是渐近稳定或者一致最终有界稳定的，即当t→∞ 时，q→0，ω→0，α→0，η→0，或者当t→∞ 时，q与ω收敛到原点的一个较小邻域内。

动态输出反馈一般采用补偿的设计方法，具有全局反馈及可靠镇定的效果，且对转动惯量的摄动及外力扰动变化具有一定的鲁棒性。充液航天器控制系统是一个参数不确定系统，航天器姿态角及角速度是可以测量的状态向量，而等效液体模型的晃动模态为不可测的状态向量。本文针对这类不确定系统的控制问题，运用自适应方法得到了弹簧质量模型的状态向量的最优估计值并设计出了自适应动态输出反馈控制器，

假设1.对于存在有干扰力矩的充液航天器姿态控制系统，外部扰动Td具有连续性及一致有界性，满足如下条件

式中:β为沿着三个坐标轴关于 Td2的最大未知边界。

设计如下控制器［12］

式中:Qi为待设计的正定对称矩阵，有Qi=＞0，β^为 β无限接近的估计值，单位向量a=［1 1 1］T，K、D为待设计控制增益，η^i为 ηi无限接近的估计值，α^i为αi无限接近的估计值，qe=［qe1qe2qe3］T为指令四元数qc与输入四元数 q的姿态误差。

控制反馈增益可以设计为

式中:k＞0，d＞0。

根据四元数的性质，qe有如下表达形式

下面证明系统的稳定性，构造李雅普诺夫函数

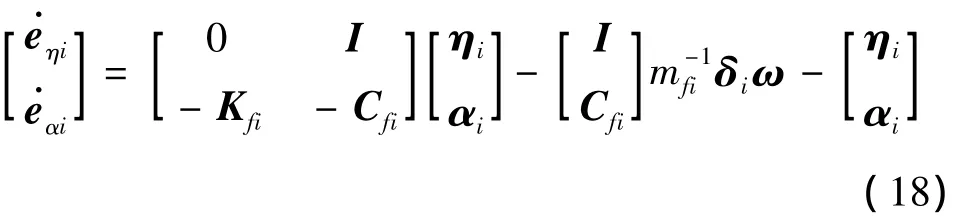
将李雅普诺夫函数对时间求一阶导数，并且将式(7)、(14)和(18)代入到式(17)中，为了得到˙V≤0，结合式(18)及假设1，进一步整理，得到^β、^αi，及^ηi自适应律

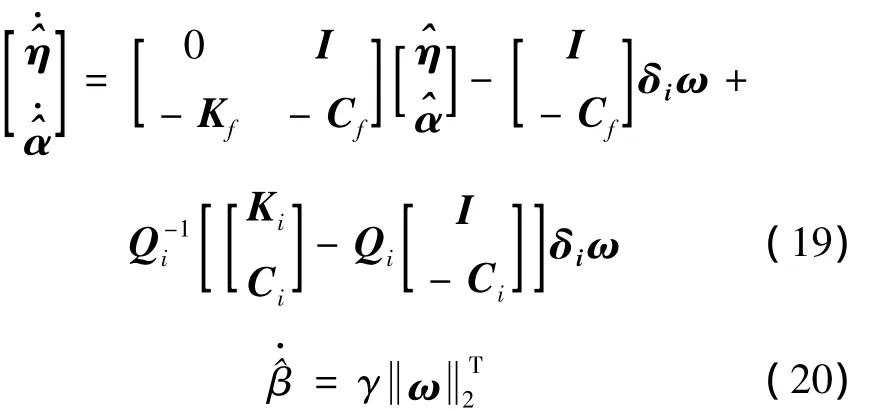
此时李雅普诺夫函数对时间求一阶导数可以表示为如下形式

式中:Ri与Qi有如下关系

可以证明系统渐近稳定。

2. 2 多模态输入成型

输入成型器是通过改变期望输入的形状和作用点位置，使得系统达到预定位置的同时，不会出现颤振现象。即通过整型之后的系统输入不仅可以满足刚体的需求，而且可以抑制液体的晃动现象。对于线性系统，设计单个脉冲的响应可描述为

式中:Qi的具体表达式可通过Matlab线性不等式模块求出。

综上，可以得到

根据LaSalle不变原理，此时，系统状态收敛于最大不变集Ξ中，其中Ξ包含于

式中:yi(t)是输出，Ai是幅值，ti为时间，ωf为无阻尼系统的频率，ζ为系统的阻尼。为了使系统在多个脉冲作用下的响应最终相互抵消而趋于零，则必须满足

具有一定鲁棒性的三阶脉冲ZVD成型器，有如下形式

以上分析仅仅考虑了系统存在单个模态的情况，对于多阶振动模态的系统，输入成型器可以先设计抑制各个单独振动模态的成型器，然后将这些成型器卷积起来，从而得到一个新的成型器

式中:*表示卷积运算。

3 数值模拟

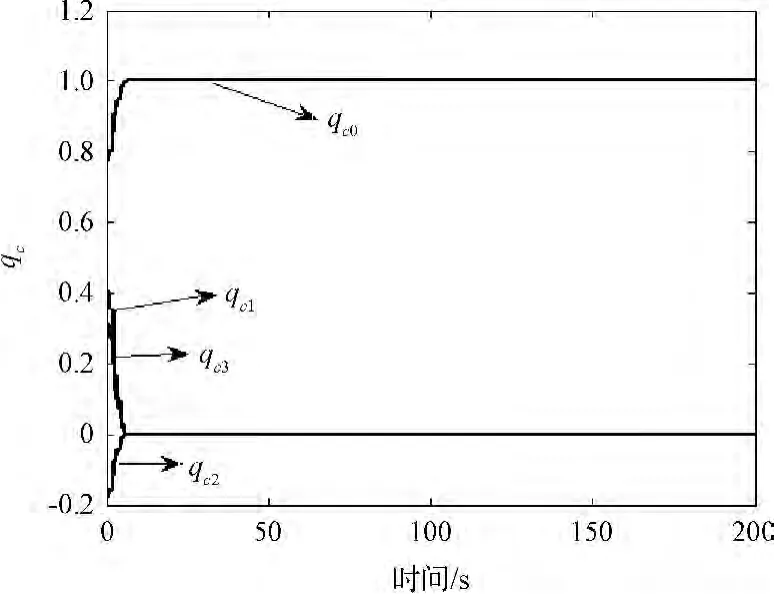
图3 成型后的姿态四元数输入指令Fig.3 Time vs shaped input command quaternions

对于三轴稳定充液航天器，根据以上的数值仿真试验，通过比较自适应动态输出反馈控制器，以及将其与二阶模态ZVD输入成型技术相结合所得到的复合控制器这两种控制方法的控制效果图，可以得到如下重要的分析结果和结论:

(1)从图4及图5所给出的航天器姿态角速率及姿态四元数响应图可以看出:系统在110 s左右达到稳定效果。仿真图还表明带有多模态输入成型技术的复合控制控制器可以稍快达到稳定;而由自适应动态输出反馈控制器(14)所得到的控制效果与复合控制器所达到的控制效果几乎相当，这也从另一角度说明自适应动态输出控制器具有较好的鲁棒性、稳定性及抗干扰的能力。

图4 姿态角速率的响应Fig.4 Time vs angular velocities response

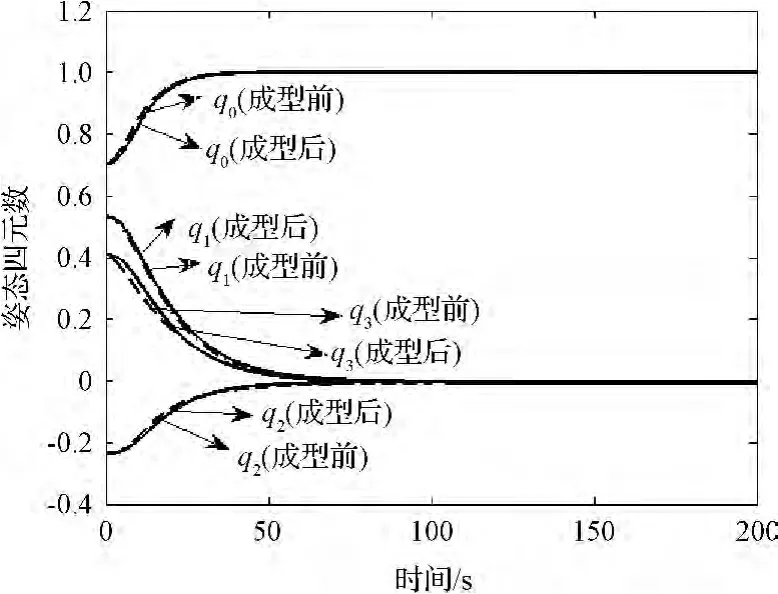
图5 姿态四元数的响应Fig.5 Time vs attitude quaternions responses

(2)从图6及图7所给出的采用成型器技术前后液体燃料晃动动力学响应图可以看出:液体晃动沿着偏航轴、滚动轴的一阶晃动的瞬态响应特征非常明显;虽然二阶晃动响应幅值比一阶晃动幅值小10－1数量级，但也显示出其不可忽略的瞬态响应特性。仿真结果显示，本文所设计的基于成型器技术的复合控制器对液体晃动的抑制效果非常明显。

(3)图8给出了采用控制器(14)时的控制力矩输入时变图，图9为采用复合控制器时的控制力矩输入时变图。在数值仿真的实施过程中，为了结合航天器工程应用实际，本文还考虑了控制力矩的饱和约束条件;控制力矩约束范围限制在－5～5 N·m之间。对比仿真图8、图9可以发现:加入成型器后的复合控制器将使航天器系统更快达到稳定姿态且控制过程中所需要的控制力矩输入更小。

图6 液体一阶晃动时域曲线Fig.6 Time vs first mode displacement of fuel slosh

4 结论

图7 液体二阶晃动时域曲线Fig.7 Time vs second mode displacement of fuel slosh

图8 控制器(14)下的控制力矩Fig.8 Control moment input under controller(14)

图9 控制器(14)结合输入成型的控制力矩Fig.9 Control moment input under controller(14)and input sharpening

本文以三轴稳定充液航天器为研究对象，在航天器的3个主惯性轴上各装一个动量轮，提供航天器的控制力矩。液体贮箱假定为椭球形，将晃动液体等效为二阶弹簧－质量模型，应用动量矩定理建立了充液航天器耦合系统动力学方程。针对充液航天器大角度姿态机动问题，设计了自适应动态输出反馈控制器，该控制器具有良好的稳定性及鲁棒性品质。为了在对航天器进行姿态机动过程自适应控制的同时，达到对储腔中的液体晃动进行抑制的目的，本文设计了具有鲁棒特性的二阶ZVD输入成型器。数值仿真试验所给出的控制效果图校验了本文方法的有效性;本文所得到的结果具有理论意义和工程应用参考价值。

［1］ 岳宝增，宋晓娟.具有刚－柔－液耦合的航天器动力学研究进展［J］.力学进展，2013，43(1):162－172.［Yue Baozeng，Song Xiao-juan.Advances in rigid-flexible-liquid-control coupling dynamics of spacecraft［J］.Advances in Mechanics，2013，43(1):162 －172.］

［2］ 李青，马兴瑞，王天舒.非轴对称贮箱液体晃动的等效力学模型.宇航学报，2011，32(2):242－249.［Li Qing，Ma Xing-rui，Wang Tian-shu. Equivalent mechanical model for liquid sloshing in non-axisymmetric tanks［J］.Journal of Astronautics，2011，32(2):242 －249.］

［3］ 黄华，杨雷，张熇，等.航天器贮箱大幅液体晃动三维质心面等效模型研究［J］.宇航学报，2010，31(2):55－59.［Huang Hua，Yang Lei，Zhang He，et al.Research on 3D constraint surface model for large amplitude liquid sloshing on spacecraft tank［J］.Journal of Astronautics，2010，31(2):55－59.］

［4］ 岳宝增，祝乐梅.携带晃动燃料柔性航天器姿态机动中的同宿环分叉研究［J］.宇航学报，2011，32(5):991－997.［Yue Bao-zeng， Zhu Le-mei. Heteroclinic bifurcations in attitude maneuver of slosh-coupled spacecraft with flexible appendage［J］.Journal of Astronautics，2011，32(5):991 －997.］

［5］ 吕敬，李俊峰，王天舒，等.充液挠性航天器俯仰运动分岔特性初步研究［J］.工程力学，2008，25(4):200－203.［Lv Jing，Li Jun-feng，Wang Tian-shu，et al.Bifurcation of a liquidfilled spacecraft with elastic appendages［J］.Engineering Mechanics，2008，25(4):200 －203.］

［6］ Kang J，Coverstone V L.Analytical model for momentum transfer of spacecraft containing liquid ［J］.Journal of Guidance，Control，and Dynamics，2010，33(3):991 －994.

［7］ 马兴瑞，韩增尧，邹元杰，等.航天器力学环境分析与条件设计研究进展［J］.宇航学报，2012，33(1):1－12.［Ma Xing-rui，Han Zeng-yao， Zou Yuan-jie， et al.Review and assessment of spacecraft mechanical environment analysis and specification determination［J］.Journal of Astronautics，2012，33(1):1 －12.］

［8］ Reyhanoglu M，Hervas J R.Robotically controlled sloshing suppression in point-to-point liquid container transfer［J］.Journal of Vibration and Control，2013，19(14):2137 －2144.

［9］ Pridgen B，Bai K，Singhose W.Slosh suppression by robust input shaping［C］.The 49th IEEE Conference on Decision and Control，Atlanta，USA，Dec 15 －17，2010.

［10］ 董锴.航天器推进剂晃动的动力学建模与抑制方法［D］.哈尔滨:哈尔滨工业大学，2009.［Dong Kai.Research on dynamic modeling and suppression strategy of propellant sloshing in spacecraft［D］.Harbin:Harbin Institute of Technology，2009.］

［11］ Yue B Z，Zhu L M.Hybrid control of liquid-filled spacecraft maneuvers by dynamic inversion and input shaping［J］.AIAA Journal，2014，52(3):618 －626.

［12］ Sales T P，Rade D A，de Souza L.Passive vibration control of flexible spacecraft using shunted piezoelectric transducers［J］.Aerospace Science and Technology，2013，29(1):403－412.

［13］ Reyhanoglu M，Hervas J R.Nonlinear control of space vehicles with multi-mass fuel slosh dynamics［C］.The 5th International Conference on Recent Advances in Space Technologies，Istanbul，Turkey，June 9 －11，2011.