测量平差中若干易混淆问题的教法研究

2015-12-14鲍建宽

测绘工程 2015年8期

鲍建宽

（黑龙江工程学院测绘工程学院，黑龙江哈尔滨150050）

误差理论与测量平差基础是测绘工程、地理信息、航测与遥感等测绘类专业的一门专业技术基础课。课程内容融合了高等数学、线性代数、概率论与数理统计、测量学等几门课程的基础知识，理论与实践并重，是测量数据处理的重要手段和主要方法。该课程的教学质量和效果，对后续的其它测绘专业课程的学习以及从事测绘生产和科研工作都具有重要影响。

测量平差基础作为一门用于处理测量数据的应用数学，具有较强的理论性，概念抽象、方程复杂、公式繁多，内容单调枯燥，学习入门较难。但其内容也有逻辑性较强的特点，只要正确理解掌握其基本原理和概念的意义、背景和适用条件，记忆一些符号的表示约定，就比较容易明了课程的整体内容体系以及各部分内容间的关系，进而明了测量平差解决测量实际问题的方法步骤。本文就测量平差基础教学内容的一些重要问题进行探讨。

1 误差理论的问题

1.1 中误差概念的理解

中误差（或方差）是误差理论的重要基本概念之一，是衡量测量精度的一个最常用指标。方差是概率论与数理统计中的概念，其定义为

方差的平方根即为中误差

它反映随机变量的取值在其中心位置附近的分散程度。依据观测误差的性质，把中误差引入到误差理论中，作为衡量观测精度的绝对指标。但在学习过程的一些实际应用中，往往混淆中误差与真误差的区别与联系。

例如，已知A，B两点间的高差为1.500m（可视为真值），在相同观测条件下进行两次测量作业，结果为：h1＝1.501m；h2＝1.495m。试问哪一个结果的测量精度高？正确结论应是精度相同。但一些同学认为h1偏离真值1mm（真误差Δ1＝-1mm），而h2偏离真值5mm（真误差Δ2＝5mm），h1当然优于h2，亦即h1精度高。这就是理解中误差的概念出现了错误。在关于真误差与中误差概念的教学时，应特别说明以下几个方面：

1）真误差是真值与观测值的差值，是一个具体的观测结果。在相同观测条件下，真误差有大有小、有正有负，只要不超过限值都是偶然误差（合格观测值），且精度相同。若观测条件不相同，比较两个真误差的大小是无意义的，亦即其值的大小不能表示与精度之间的关系。

2）为了衡量在一定观测条件下，观测值偏离真值的平均值，亦即真误差（偶然误差）偏离0值的平均值，采用真误差绝对值的平均值—平均误差为指标。注意平均误差不是中误差的平均值（因偶然误差具有对称性，平均值趋于0），而是真误差绝对值的平均值。由于计算中有绝对值，不方便后续的方程、公式的推导，所以测绘学中不常采用此指标。

3）中误差在一定意义上类似平均误差，同样反映在一定观测条件下，观测值偏离真值的平均值。计算解释：一组真误差（偶然误差）有正有负，取真误差的平方值（全部为正值，类似取绝对值），计算真误差平方值的平均值——方差，方差的平方根即为中误差。

4）真误差是一个具体的观测结果，其大小只要不超过限差皆可接受，无关精度。而中误差是根据一组相同条件下获取的真误差统计出的一个指标值，其大小反映一定观测条件下偶然误差取值大小的分布，即精度的高低。

1.2 根据双观测值之差计算单位权中误差的方法

根据双观测值之差计算单位权中误差的算式为

在实际应用中，对式（3）中分母的2是要还是不要往往有争议。例如，为检测一幅地形图的测量精度，检测了50个地物点的坐标，把检测点展绘到地形图上，量取检测点和对应原地物点间距为di（i＝1，2，…，50），试统计地形图的测量精度，应如何计算。

其实，对于式（3）的适用条件是很清楚的：同一个量在相同条件下观测两次（称为一个观测对，其精度相同，权都是pi），其差值为di，根据n个观测对的结果计算单位权中误差的算式即为式（3）。对于前述的例子，计算测量精度时，首先要明确检测时的测量条件，如果检查时和原来测图时的条件（仪器、方法）相同，即符合式（3）的适用条件；如果检测时采用的仪器比原来测图仪器精度高出一级，计算测量精度时就不能采用式（3），要去掉式中的2，此时的d已不是双观测值之差，其实就是真误差。

1.3 误差传播率的计算问题

1）误差传播率的含义。在学习误差传播率时，首先要明确误差传播率的含义：反映观测量的精度与其函数的精度之间的规律，称为误差传播率，即误差传播率是解决依据观测量的精度指标计算观测量函数的精度指标的问题。精度指标有方差、协因数，相应的就是方差传播率和协因数传播率。要注意的是，没有权的传播率要计算权，先依据协因数传播率计算协因数，再由权与协因数的关系求权值。

2）传播率的公式记忆方法。方差传播率的矩阵表达式为

初学者往往不易记住公式的具体形式，其实注意两点即可：第一，函数的方差阵等于函数的系数阵、观测量的方差阵和系数阵的转置矩阵三个矩阵的乘积；第二，根据各矩阵的维数和矩阵可乘的条件判断记忆公式的正确性。此外，还可以用下面的方法记忆传播率公式。

对于观测量xi的线性函数y，其纯量表达式为

对式（5）进行微分（对非线性函数亦然），并用真误差表示为

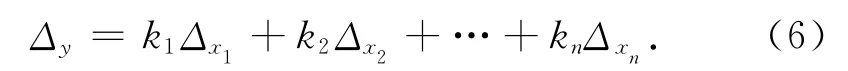
若用矩阵表示观测量的函数，则

把式（7）表示为真误差之间的关系式：ΔY＝KΔX，并转置得两式相乘得

协因数传播率的形式和方差传播率的形式是一样的，只需把方差、协方差替换为协因数和互协因数即可。

3）利用传播率解决实际问题的计算步骤。

第一步：明确观测量，表示出观测向量X，写出观测向量的方差阵DXX；

第二步：建立待求量Y与观测量X 的函数关系，见式（8）。若为非线性函数要线性化（全微分即可）；

第三步：利用式（4）进行计算，计算时注意单位的统一。

在“误差传播率的应用”教学中，强调上述三个步骤，按此思路，则无论是一般的误差传播率计算问题还是实际应用问题，都能做到思路清楚、顺利解题。即便是在各种平差法中的精度评定问题亦是如此。

1.4 有关误差理论的作业练习

在教学过程中对有关误差理论的概念、计算方法、实际应用等问题，通过重点分析讲解、总结讨论以助理解，这仅是学习的一个环节，还要通过适当的作业练习来强化巩固学习效果。如果作业练习不够，往往是看着明白，一旦遇到问题就没了思路、无从下手。对作业习题要有一定的数量保证外，还要在练习题的设计上下功夫，首先是针对单一概念的简单问题，然后是面向实际应用的综合性问题。

2 平差方法的问题

2.1 必要观测个数的确定方法

确定平差问题中的必要观测个数，是正确建立平差函数模型的第一步，也是关键的一步。对这个问题，初学者往往理解不透，特别是一些复杂的控制网。在教学中明确以下概念有助于此类问题的解决：

1）必要元素：或称为必要量，是唯一确定模型所必须知道的元素，个数用tm表示。

2）必要观测元素：或称为必要观测量、必要观测值，是指必要元素中需要观测才能确定的量，个数用t表示。

3）必要起算元素：或称为必要起算数据、配置元素，是指在必要元素中不能通过本次（期）观测作业获得的量，个数用t0表示。

上述三者的关系是：t＝tm-t0，这个关系式也是确定必要观测个数的基础。如果平差问题中的起算数据除去必要的以外，还有tr个多余的起算数据，则必要观测个数相应的要减少tr个，即

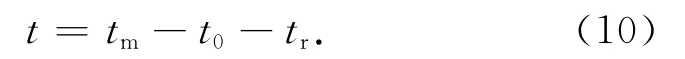
只要明确各类控制网的tm，t0个数，据式（10）就很容易确定必要观测个数。

水准网：tm＝总点数，t0＝1（一个点的高程），tr＝（已知点数-1）＋已知高差个数；

平面测角网：tm＝总点数×2，t0＝4（一个点的平面坐标、一条边长、一条边的方位角），tr＝2（已知点数-1）＋（已知边个数-1）＋（已知方位角个数-1）＋固定角个数；

平面测边网：与平面测角网相同，只是t0＝3；

平面测方向网：与平面测角网相同，只是tm＝总点数×2＋测站点个数；

观测坐标的平面网（平面图形数字化）：tm＝总点数×2，t0＝0，tr＝固定角个数＋固定边个数；

GPS网：tm＝总点数×3，t0＝3（一个点的三维坐标），tr＝3（已知点数-1）。

2.2 条件方程的列立原理

在必要观测的基础上，每增加一个多余观测就产生一个条件方程。条件方程产生的根本原因是：因为多余观测值的存在，使得同一个量有两个值为Z与Z′，这两个值就起到了检核作用，其平差值应相等，或者其平差值的差值应为0。这就是条件方程列立的基本原理，表示为

例如，三角形图形条件：测量2个角度即可确定三角形，再增测一个角度，由于三角形内角和已知为180°，测三个角亦可计算出三角形内角和，则内角和的测量值与已知值就产生一个检核条件，即为图形条件。

同理可列出平面网的水平条件（圆周条件）、极条件、坐标条件、方位条件、边长条件、正弦条件、余弦条件等等。

2.3 误差方程的列立原理

把观测方程式（12）线性化，即得误差方程。

2.4 精度评定的内容与方法

精度评定的内容与计算方法，在各种平差法中的计算内容一样，计算方法略有不同。依据权的定义，可得

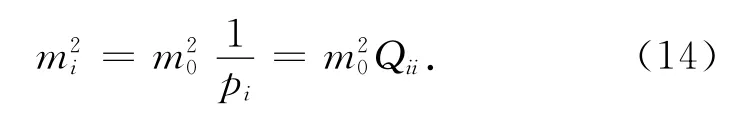
由式（14）可见：要计算某量的方差，只要计算出单位权方差和该量的协因数即可。计算单位权方差和待求量的协因数，即为精度评定的内容。

2.4.1 单位权方差的计算

单位权方差的算式为

所有最小二乘平差法中，单位权方差的算式都是式（15），只是VTPV值的计算方法，如果不由V直接计算，间接计算VTPV值的方法有一些差异。

2.4.2 某量平差值的协因数计算

计算某量平差值的协因数的方法，亦遵从传播率计算的三个步骤。第一步，为了计算方便，此时的观测值不用原始观测值L，而是观测值L的函数：条件平差时用观测值的平差值，其协因数为＝Q-QA；间接平差时用参数平差值，其协因数为＝；第二步，建立待评定精度的量与观测值（非原观测值L，而是或）之间的函数关系式，此处称为权函数式。条件平差的权函数式为：；间接平差的权函数式为：＝；第三步，利用传播率式（4）进行计算。最后，由式（14）计算的方差及中误差。

2.5 有关平差方法的作业练习

由于测量平差实践性强，实际应用中计算量大。在教学过程中，为加强对平差方法的理解掌握，除做一些控制网必要观测个数和多余观测个数的确定、各类条件方程的建立方法、各类误差方程的建立方法、各种平差方法的法方程组成与计算、平差值的计算方法、精度计算的方法等单项练习外，还要有测绘工程项目控制网平差的综合性练习。由于综合性平差练习计算量大，在集中练习时手工计算会花费很多时间，往往让学生学习现有平差软件并用平差软件完成较大型平差问题的解算。这样很不利于学生对平差过程的理解与掌握，起不到强化学习的过程，反而认为平差课程无用。在做这类大型习题练习时，若沿袭手工计算方法是不合时宜的，而仅仅练习一下平差软件的用法也是不可取的。由于在平差课程学习以前，学生至少已经熟悉office excel的一般内容（甚至有些还同时学习matlab课程），利用excel的函数计算功能，让学生在excel表格上分步完成控制网平差。这样，在表格上完整展现整个平差过程、各计算步骤之间的数据关系与流程，有手工计算表格清楚反映计算过程的优势，而没有手工计算繁杂量大的缺点。既强化对平差理论与方法的理解，又初步建立软件设计的概念。最后介绍、使用现有平差软件，更能让学生认识实现测量平差自动化、智能化的优势与途径。

3 结束语

误差理论与测量平差基础课程具有理论性强、教材中概念抽象、公式和名词术语较多、内容显得散乱，而逻辑性较强的特点，使得初学者入门困难。在教学过程中，必须在教学体系、教学内容、教学方法和教学手段等方面的改革上下功夫，投入较大精力进行探索研究。还要基于课程特点，依据内容的逻辑关系，首先了解课程的主要内容框架，再依各内容模块进行教学，注重理解基本概念的意义和适用条件、相关内容的系统性，并加强作业习题练习，以提高本课程的教学质量与效果。

［1］朱建军.误差理论与测量平差基础［M］.北京：测绘出版社，2013.

［2］张明华.面向经济建设的测绘工程专业课程体系探讨［J］.测绘工程，2013，22（6）：93-76.

［3］鲍建宽.平差数学模型教学改革的探讨［J］.测绘工程，2007，16（6）：71-73.

［4］刘志平，张书毕，卞和方.经典平差函数模型的概括形式分析［J］.测绘工程，2015，24（3）：78-80.

［5］姚宜斌，邱卫宁.测量平差问题中必要观测数的确定［J］.测绘通报，2007（3）：14-16.

［6］张俊，张鹏飞.测量平差课程教学改革探讨［J］.测绘科学，2010（5）：247-249.

［7］邓兴升.提高测量平差课程教学质量的措施［J］.测绘工程，2010，19（6）：74-76.

［8］丁克良，陈秀忠，杜明义.测量平差课程教学若干思考［J］.测绘科学，2009（4）：217-218.

［9］张俊，袁亮，张鹏飞.条件平差和间接平差模型应满足的两个等式关系［J］.测绘与空间地理信息，2014，37（12）：86-87.

［10］张俊，独知行，张显云.测量平差双光滑参数解算半参数模型的研究［J］.测绘科学，2014，39（5）：96-98.

［11］宋迎春，左廷英.在“测量平差”课程教学中融入数学建模思想的探讨［J］.现代测绘，2009（9）：46-48.

［12］陶本藻.广义逆矩阵与测量平差［J］.测绘工程，2000，9（12）：10-13.