新陈代谢GM（1，1）模型在大坝边坡沉降监测中的应用

曾贤敏，黄 腾，李桂华，周 帆

（河海大学 地球科学与工程学院，江苏 南京210098）

灰色预测［1］是指对系统行为特征值的发展变化进行的预测，对既含有已知信息又含有不确定信息的系统进行预测，在一定范围内变化的、与时间序列有关的灰过程进行预测。使用最广泛的灰色预测模型就是关于数列预测的一个变量、一阶微分的GM（1，1）模型，GM（1，1）模型对时间序列短、统计数据少、信息不完全系统的建模与分析，具有独特的优越性［2-4］。

目前，工程界进行沉降预测主要采用GM（1，1）模型，传统的GM（1，1）模型存在不足，对于任何一个灰色系统而言，随着时间的发展，会出现一些扰动因素不断地对系统产生影响，所以传统的GM（1，1）模型对于原始序列之后的1、2期数据有较高的预测精度，可越往后预测意义就越低。为了弥补上述缺陷，引入了新陈代谢GM（1，1）模型，一方面它继承了传统GM（1，1）模型的优点，另一方面它能更新数据序列的初始值及时系统的扰动因素考虑进去，去掉失去预测意义的老数据对原始时间序列进行新陈代谢，提高模型的预测精度。

本文以南方某大坝边坡监测点的沉降位移为例，用新陈代谢GM（1，1）模型对沉降位移进行拟合预测，事实证明其拟合预测精度高于传统GM（1，1）模型，值得推广使用。

1 建立模型

1.1 传统 GM（1，1）模型

传统GM（1，1）模型是基于随机的原始时间序列，经按时间累加后形成的新的时间序列呈现的规律可用一阶线性微分方程的解来逼近。传统GM（1，1）预测模型的建立［5］：

设非负离散等间隔数列为

对x（0）作一次累加

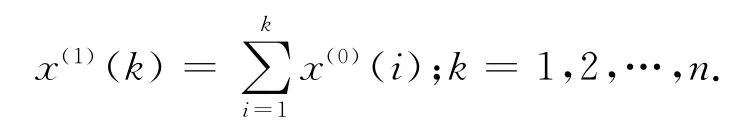
得到生成数列为

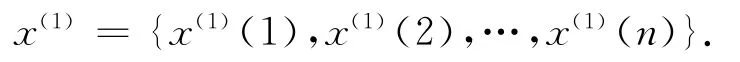
于是x（0）（k）的 GM（1，1）白化微分方程为

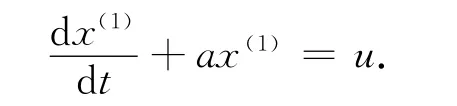
式中：a，u为待定参数，a为发展系数，反映x的发展趋势；u为灰色作用量，反映数据间的变化关系。并记a，u构成的矩阵为灰参数

对累加生成数据做均值生成B与常数项向量Y，即

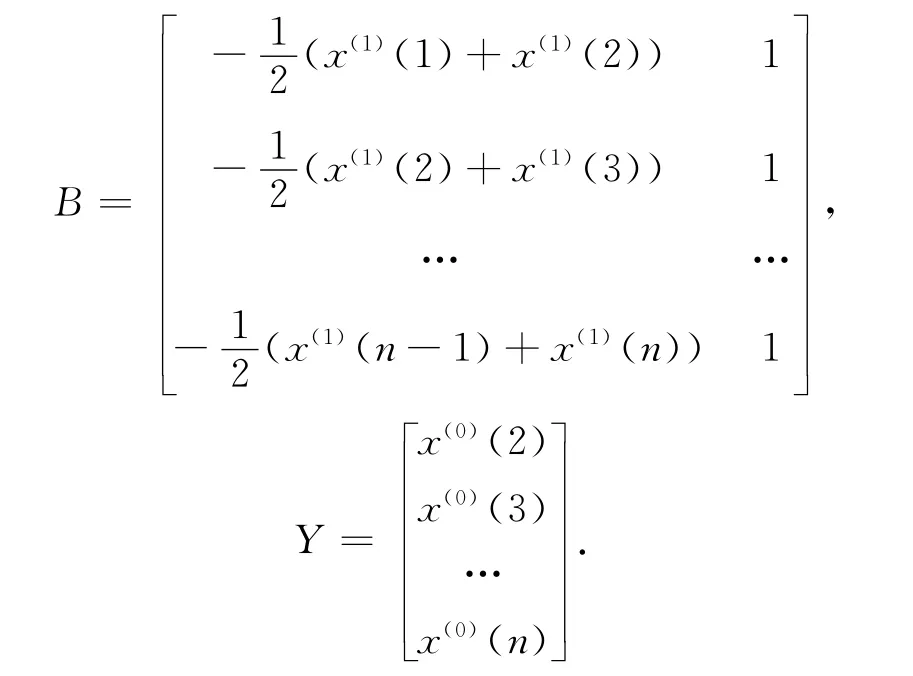
还原原始数据得

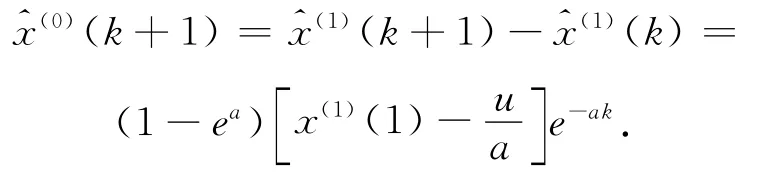
1.2 新陈代谢GM（1，1）模型

灰色新陈代谢GM（1，1）模型是将原始时间序列更新改进传统GM（1，1）模型。其建模原理为将传统 GM（1，1）模型中的原始序列x（0）＝ ｛x（0）（1），x（0）（2），…，x（0）（n）｝的最老信息x（0）（1）去除，同时置入最新数据 x（0）（n＋1），用全新的数据序列x（0）＝｛x（0）（2），x（0）（3），…，x（0）（n＋1）｝重 新 建 立GM（1，1）模型，进行一维新陈代谢GM（1，1）预测，如此反复，随着时间序列的发展，依次递补建立n维新陈代谢模型，直到完成预测目标达到预测精度，即为灰色新陈代谢GM（1，1）模型。

2 模型精度检验

模型的检验是模型建立后必不可少的工作，常用的灰色预测模型检验方法一般有残差检验，关联度检验和后验差检验。本文采用残差合格模型［6-10］评判模型精度，该检验法是由相对误差和平均相对误差共同描述。设原始序列为

用经过预测得到的模拟序列：

则残差序列为

可得相对残差序列：

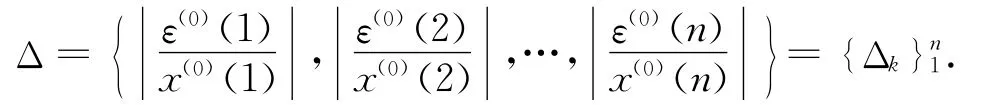
表1 精度检验等级参照表

3 实例分析

本文以南方某大坝边坡监测点的沉降监测数据为例验证新陈代谢GM（1，1）模型在大坝边坡沉降监测中应用的可行性。其所测数据见表2。

自2013-05-01开始每隔15d进行一次观测，本文取前11期监测数据资料进行实验。使用前8期观测数据作为原始时间序列建立传统GM（1，1）模型，对前8期的数据进行拟合并预测第9～11期数据。然后建立一维新陈代谢GM（1，1）模型，去除第1期数据加入第9期数据，用更新过的数据序列再次建立GM（1，1）模型，对第2～8期数据进行拟合并预测第9～11期数据，依次递补建立n维新陈代谢模型直到满足预测精度要求。本次实验计算均通过MATLAB R2008a编程完成。

表2 监测点沉降监测资料

3.1 建立传统GM（1，1）模型

使用大坝边坡监测点前8期沉降监测数据作为原始时间序列：

对x（0）作一次累加得

进而得到原始数据：

3.2 建立新陈代谢GM（1，1）模型

去除第1期监测数据，使用第2～9期监测数据作为原始时间序列：

使用新x（0）建立一维新陈代谢 GM（1，1）模型可得到原始数据：

同理使用第3～10期监测数据建立二维新陈代谢GM（1，1）模型得到原始数据：

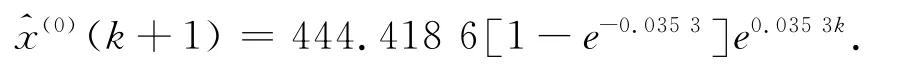
3.3 模型精度分析

分别使用上述建立的三种模型对前8期数据进行拟合，结果如表3所示。

表3 拟合效果检验表

利用残差合格模型对模拟效果进行精度评定，可以看到传统GM（1，1）模型中相对误差Δ8＝1.98%，平均相对误差属于二级精度，利用同类方法对其他两种模型的模拟效果进行精度评定，评定结果如表4所示。

表4 拟合效果精度评定表

通过表3可知，拟合值与实际值的最大残差出现在传统GM（1，1）模型中，二维新陈代谢 GM（1，1）模型拟合值残差最小。通过表4可知，新陈代谢GM（1，1）模型拟合精度要高于传统GM（1，1）模型，且随着新陈代谢维度的增加拟合精度也会越高，一维新陈代谢GM（1，1）模型已经达到一级精度要求，二维新陈代谢GM（1，1）模型的拟合精度高于一维新陈代谢GM（1，1）模型，达到预期拟合效果。

通过以上实验可得新陈代谢GM（1，1）模型拟合精度高于传统GM（1，1）模型，分别利用以上模型对第9～11期观测数据进行预测，预测结果如表5所示。

表5 预测效果检验表

利用残差合格模型对模拟效果进行精度评定，评定结果如表6所示。

表6 预测效果精度评定表

观察表5，新陈代谢GM（1，1）模型预测值与实际值残差小于传统GM（1，1）模型，预测效果也逐步提高。通过表6可知，新陈代谢GM（1，1）模型预测精度高于传统GM（1，1）模型，且随着新陈代谢维数的增加预测精度也会越高，二维新陈代谢GM（1，1）模型预测精度达到一级，达到预期效果。

4 结 论

GM（1，1）模型已经成为工程界对沉降监测位移进行预测的重要方法，在利用传统GM（1，1）模型进行预测时必须看到它的不足之处，重视建筑物在发展过程中随时进入的扰动因素，由此引入新陈代谢GM（1，1）模型。本文结合南方某大坝边坡监测点的沉降位移为例建立传统GM（1，1）模型与新陈代谢GM（1，1）模型分别进行拟合预测。通过对比分析可得：

1）沉降预期结果的精度取决于预测模型的选择，本文通过去除老数据加入最新数据建立的新陈代谢GM（1，1）模型在预测时融入了未来的噪声，避免传统GM（1，1）模型预测值由随着时间的发展与实际值偏差越来越大，而失去预测的意义。

2）新陈代谢GM（1，1）模型对大坝边坡沉降位移模拟预测精度明显高于传统GM（1，1）模型，且随着时间序列的更新精度越高，二维新陈代谢GM（1，1）模型的模拟预测精度可达到一级，说明新陈代谢模型进行模拟预测时合理可靠，值得类似工程借鉴使用。

［1］邓聚龙.灰色系统理论简介［J］.内蒙古电力，1993（3）：51-52.

［2］唐佑辉，黄腾，赵兵帅.GOM和时间序列组合模型在地表沉降预测中的应用［J］.测绘工程，2014，23（2）：70-72.

［3］赵福洪，罗志清，杨建文.七种数学模型在沉降预测中的优缺点比较分析［J］.测绘工程，2014，23（3）：59-62.

［4］邱伟，黄腾，朱春宁.混合模型在沉降监测中的组合预测方法［J］.测绘工程，2014，23（4）：51-54.

［5］肖文，范志平，蔡仁澜，等.灰色系统 GM（1，1）模型在建筑物变形监测中的应用［J］.地理空间信息，2010（2）：148-150.

［6］臧德彦.灰色系统理论在海堤沉降预测中的应用［J］.测绘工程，1999（2）：50-54.

［7］刘树，王燕，胡凤阁.对灰色预测模型残差问题的探讨［J］.统计与决策，2008（1）：9-11.

［8］陶家祥，张博，胡江.改进的GM（1，1）模型在大坝监测数据预测中的应用［J］.水电能源科学，2011（5）：70-72.

［9］何伟，李明，阚起源.抗差加权非等时距 GM（1，1）模型在大型建筑物沉降预测中的应用［J］.测绘工程，2014，23（4）：62-64.

［10］张怡，魏勇，熊常伟.灰色模型GM（1，1）的一种新优化方法［J］.系统工程理论与实践，2007（4）：141-146.