基于局部体样条函数的海洋盐度场建模

杨振发，万 刚，李 锋，张宗佩

（信息工程大学，河南 郑州450001）

随着时代的发展，海洋对各国的价值日益凸显，战略地位不断提升，特别是进入21世纪后，各国正加快步伐，建立“数字海洋”。海水盐度是海洋水文要素的重要组成部分，其在垂直方向和水平方向的变化，直接影响舰艇声纳的工作距离和舰艇的航行速度和日数。

将海洋盐度的数据场进行可视化表达既可以形象逼真的展现数据本身的结构特征，又可以通过交互等操作辅助人员做出合理的判断，而数据场科学可视化的关键在于数据的建模。针对海洋盐度场的散乱大数据场建模，国内外文献归纳的建模方法大致可以分为两种：一种是层次化方法，分为基于多层B样条插值方法［1-2］和多分辨率方法［3］，前者正在解决双变量数据建模的问题，而后者作为提高大数据可视化的交互手段，主要用于复杂模型的简化；另一种是局部化方法，包括基于体数据的最小范数网络法［4］和局部体样条函数法［5］，前者建模精度高，但实现需要一个四面体化的算法和一个复杂的迭代方法，而后者将大数据场局部化成小区域，采用适用于中小数据量的体样条函数建模方法，该方法精度高，且易于实现，但关键问题在于解决如何将区域适当地分割。

针对以上适用于海洋盐度散乱数据场建模方法的分析，本文在介绍海洋水文要素中的盐度数据的特点后，采用局部体样条函数法对海洋盐度场进行建模，并利用非线性规划的遗传算法，解决局部体样条函数法在散乱盐度场建模中的区域划分优化组合问题，最后通过最大密度投影算法实现建模数据的可视化表达，为海洋战场环境表达与分析提供较为形象、直观的三维盐度场仿真手段。

1 海水盐度数据特点与来源

在海洋化学中，盐度的确切定义为：“1kg海水中，所有碳酸盐转化为氧化物，溴、碘以氯置换，所有的有机物被氧化之后所含全部固体物质的总克数”，单位为g／kg［6］。海洋表面盐度分布的总规律是：从亚热带海区向高、低纬递减，并形成马鞍形曲线，赤道附近盐度较低，南北纬20°附近的盐度最高，然后随纬度的增加而降低。海水盐度垂直分布规律是：在北纬40°到南纬50°之间，是盐度垂直变化最大、最复杂的地区（见图1）。从海面到150m深度上盐度高而均匀，最大盐度值一般出现在100～300m之间，深层水的盐度分布最均匀，盐度值比表层水低、比中层水高。

图1 海水盐度场的分布规律

海水盐度场是海洋环境中不可见的水文要素，与海底地貌等数据场存在很大的区别。盐度数据主要来源于舰船的调查数据，其特点是数据分布相对离散、不规则，属于典型的大数据场的散乱体数据。而仅有这些离散的、不规则的数据难以进行盐度场的三维可视化连续表达。

2 海水盐度场的建模

散乱体数据的插值问题［7］在20世纪60年代开始引起人们的注意，经过近半个世纪的研究，已有适用于不同需求和数据类型的建模方法，且大都只是适用于中小规模的数据场建模算法。Nielson在文献［7］中通过实验证明当数据量在200～500以内时，体样条函数法对于解决数据场的建模问题相当有效，而规模超过500后，求解得到的线性方程组系数矩阵的条件数将存在问题，使得解的鲁棒性和建模精度大大降低。鉴于体样条函数法［8］在中小规模散乱数据场的建模中具有拟合精度高、易于实现等优点，因此可以将大规模数据场适当分区，分别构造建模函数，再赋予其权重并将各区“拼”成一个整体。而这种局部的体样条函数法的建模精度关键在于区域分割的优化程度，本文采用非线性规划的遗传算法来解决这个关键问题。图2为盐度场数据的建模流程。

图2 盐度场建模流程

2.1 局部的体样条函数法

为了便于建模操作，假设盐度数据的采样空间为一规则的长方体Ω＝｛P＝（x，y，z）｜a≤x≤b，c≤y ≤d，e≤z≤f｝。采样点 Pi＝ （xi，yi，zi）（1≤i≤n）的盐度数据为fi。故对盐度数据场的建模即构造一个在Ω上的连续函数F（P）＝F（x，y，z），使Pi处采样值满足F（Pi）＝F（xi，yi，zi）＝fi（1≤i≤n）。实现步骤如下：

1）将长方体区域分块。将Ω的3个方向分别划分为nx，ny，nz个分块，分块的支集为 Ωijk（0≤i≤nx，0≤j≤ny，0≤k≤nz），保证支集中的数据点数大致相同且不超过500，这将在下一节中采用非线性规划的遗传算法予以解决。

2）构造分块区域Ωijk的权函数Wijk（P）。权函数满足的条件如下：

a.当P∉Ωijk时，Wijk（P）＝0；

文献（3）采用Hermite的方法，给出具体求解权函数的方法。

3）构造分块的建模函数Fijk（P）。当数据场的数据个数小于500时，研究表明多重二次型法［9］具有拟合精度高等优点，这里采用此法构造函数。建模函数为

式中：‖P-Pi‖为插值点到采样点的距离函数；K2为实验参数，这里设为0.1；系数ai可由下面的线性方程组的解确定

2.2 非线性规划的遗传算法实现区域的优化分割

采用局部体样条函数法的前提和关键是解决大区域的分块问题，即如何将分块后的支集包含的采样点数大致相同且限制在500以下。为了解决这样一个带约束的组合优化问题，本文采用非线性规划的遗传算法［10］。

非线性规划问题是研究一个n元实函数在一组等式或不等式的约束条件下的极值问题，它具有局部搜索能力强等优点，但易于陷入局部次优解。遗传算法是一类借鉴生物界自然选择和遗传机制的随机搜索算法，它从随机产生的初始解开始搜索，通过一定的选择、交叉、变异等操作逐步迭代产生新解。群体中的每个个体代表问题的一个解，称为染色体，染色体的好坏用适应度值来衡量，根据适应度的好坏从上一代中选择一定数量的优秀个体，通过交叉、变异形成下一代群体。经过若干代进化后，算法收敛于最好的染色体，即为最优解或次优解。遗传算法在搜索时从问题解的一个集合开始，而不是单个个体，可大大减少陷入局部最小的可能性。结合以上两种算法的优缺点，非线性规划的遗传算法解决局部体样条函数法区域划分问题的算法流程如图3所示。实现的具体步骤为：

1）种群初始化。要使每个划分的数据量满足r∈（r1，r2），以X 轴向为例dx＝b-a，m＝ ［n／r1］，其划分Hx编码为dx｝，xi表示第i段的区间长度，令H＝Hx×Hy×Hz，则J＝J（H）为划分H 的一个可能解。对划分分别随机产生3个划分数量u，v，w∈［1，m-1］，使［u×v×w／m］＝1，令xi＝［dx／u］（0≤i≤u-1），其余码元值为0。

4）交叉操作算子。随机选取两个个体，通过染色体的交换组合，把父辈的优秀特征传递给子辈，从而产生优秀个体，第m个染色体和第n个染色体在l位的交叉操作为

其中，b是区间［0，1］的随机数。

5）变异操作算子。其目的是维护种群多样性，纠正遗传算法过早收敛的缺点。从种群中随机选择第i个体，第j个编码编译操作为

其中amax是染色体aij的上界，amin是染色体的下界；f（g）＝r（1-g／Gmax）2，r是随机数，g是当前的迭代次数，Gmax是最大进化次数。

6）非线性规划寻优操作。对进化代数进行判断，这里选择代数为5，当满足所定的代数时，为了加快进化，利用Matlab的规划工具箱函数进行局部搜索最优值，把所得到的局部值作为新个体继续进行进化操作。

7）终止判断条件。对所得的各代染色体进行适应度函数计算并比较，若为最大则终止进化；否则返回步骤（2）。

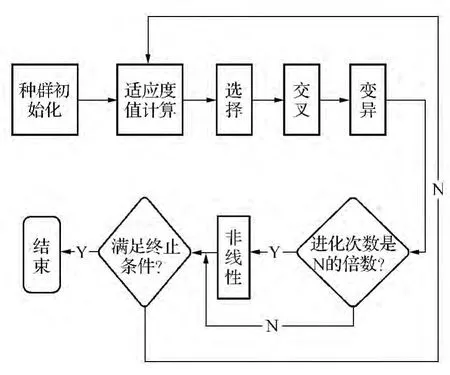
图3 非线性规划的遗传算法实现流程

3 实验及结果

从国家海洋局网站上获取大规模散乱的海洋盐度数据，利用Matlab软件的线性规划工具箱和遗传工具箱，编写M文件程序实现对数据场的基于非线性规划遗传算法的区域分块。如图4所示，图4（a）（b）（c）为散乱数据空间的三个轴向数据分块结果，整个区域被分成共48个小区域，每个区域的数据量在400～460之间。图4（d）为某一盐度层的插值函数三维可视化结果。

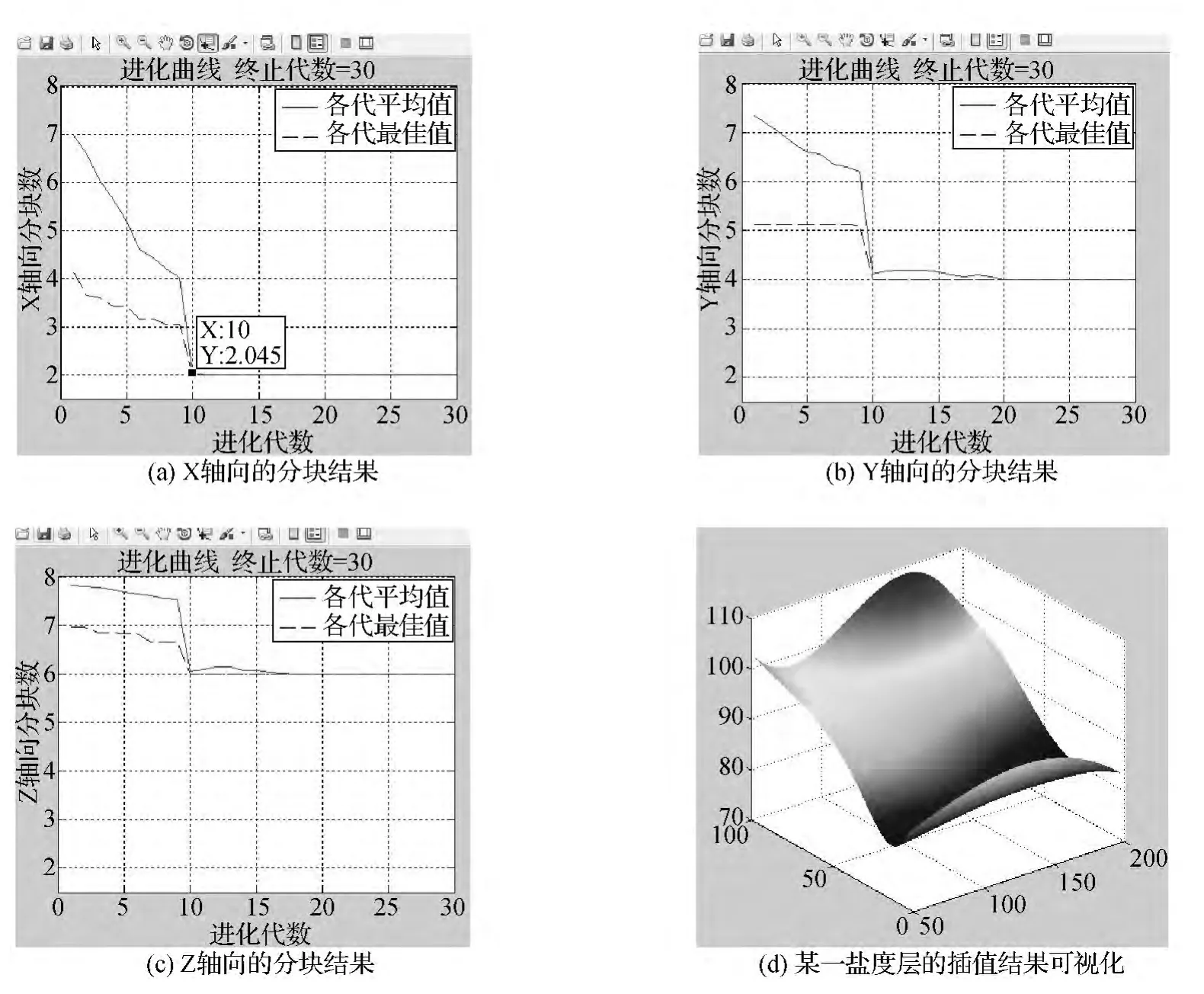
图4 局部体样条函数建模的实验结果

体绘制［11］研究的是含有物体内部信息的体数据的表示、操作和显示的问题，较之于传统的面绘制方法，体绘制方法能表达空间数据场内部的数据特征和关系，因此特别适用于盐度场数据的可视化表达。最大密度投影［12］（Maximum Intensity Projection）算法是一种被广泛应用于医学CT和MRT图像处理的体绘制算法。该方法使用光线跟踪算法［13］跟踪二维屏幕上的每一个像素所发射出的每一条射线与三维空间数据相交的每个体素，逐个进行遍历，找出每条射线中的最大数据值，无需进行光照和累加这两个过程，因此具有思路简单，便于编程实现等优点。图5给出MIP算法实现海洋盐度标量数据场体绘制的流程图，图6为MIP算法实现的某海域盐度场体视化结果。

利用上述介绍的散乱数据场建模得到的规则盐度场，利用OpenGL图形接口的可编程着色器功能，在Intel（R）Core（TM）i5CPU 2.53GHz；内存2.00GB；HD5730独立显卡的计算机上实现基于最大密度投影算法的盐度场数据体绘制。

图5 最大密度投影算法实现流程

图6 MIP算法实现的某海域盐度场体视化结果

4 结 论

针对海洋水文要素数据量大且散乱等特点，本文采用局部的体样条函数插值算法对标量数据场进行插值建模，为了解决散乱大数据场局部化建模时需满足的组合优化条件才能保证插值精度的问题，本文利用具有较强全局搜索能力的非线性规划的遗传算法，较好地解决大数据场区域适当分块的问题，最后通过Matlab工具箱编程实现区域的组合优化分割，并将得到的规则数据场通过最大密度投影算法予以可视化表达，为海洋盐度场的数据仿真提供较为可靠的仿真方法与手段。

［1］朱振华.双三次B样条曲面法在声呐测量数据空白填补中的作用［J］.测绘工程，2013，22（1）：75-77.

［2］周玉娟，岳桂昌.二次B样条修正VTEC多项式模型研究［J］.测绘工程，2013，22（3）：41-43.

［3］STAADT O G，GROSS M.Progressive tetrahedralizations［A］.In：Proceedings of IEEE Visualization98，North Carolina，1998.397-402.

［4］NIELSON G M，TVEDT J.Comparing methods of interpolation for scattered volumetric data［J］.Advanced Techniques for Scientific Visualization，ACM SIGGRAPH’94，II-99.

［5］杨冠杰，耿震，孙菁.散乱体数据可视化：海洋水团分析的新途径［J］.海洋通报，2000，19（2）：66-74.

［6］韩庆，李本江，高峰，等.海洋小百科全书［M］.中山：中山大学出版社，2012.

［7］SHEPARD D.A two dimensional interpolation function for irregularly space data［J］.Proceedings of ACM 23“National Conference，1968，517-524.

［8］NIELSON G M.Scattered data modeling［J］.IEEE CG＆A，1993，13（1）：60-70.

［9］KREGLOS O，HAMANN B.Data structures for optimizing linear spline approximations［J］.Computer ＆Graphics，2000，24（3）：353-361.

［10］唐加福，汪定伟，高振，等.面向非线性规划问题的混合式遗传算法［J］.自动化学报，2000，26（3）：401-404.

［11］KAJIYA J，VON H B.Ray tracing volume densities［J］.Computer Graphics，1984，18（3）：165-174.

［12］ELLIOT K，FISHMAN，DEREK M D，NEY R.Volume Rendering versus Maximum Intensity Projection in CT Angiography：What Works Best，When，and Why［J］.RadioGraphics，2006，26（3）：905-922.

［13］LEVOY M.Efficient ray tracing of volume data［J］.ACM Trans.On Graphics，1990，9（3）：245-261.