一种用于加速FPGA设计空间探索的电路特性驱动半监督建模方法

杨立群李 威黄志洪孙嘉斌杨海钢*

1 引言

现场可编程门阵列（Field Programmable Gate Array, FPGA）的架构对在其上实现的电路性能有显著影响。架构指FPGA内部可编程逻辑单元的结构以及逻辑单元之间的互连结构，其可由一系列的架构参数进行表征。随着工艺尺寸的缩减以及应用电路的复杂化，FPGA架构设计过程中需要考虑的架构参数日益增多。所有架构参数的组合构成了FPGA的架构设计空间，显然，从呈指数型扩增的FPGA架构设计空间中快速选择一个满足设计指标的优化架构成为FPGA设计初期需要解决的重要问题。

一种传统的架构选择方法是借助特定 CAD流程工具，例如 VTR[1]，来探索 FPGA 架构设计空间[24]-。设计空间中的所有待选架构通过VTR获得相应的性能，如面积、延时等。通过对所有架构的性能进行比较，获得最佳性能（最小面积或最小延时）的架构被选作最优架构。由于 VTR包含综合、映射、装箱、布局和布线一系列步骤[5]，并且设计空间随着架构参数增长，因此将设计空间中的每一个架构通过 VTR来获得相应的性能非常耗时且不符合工程应用实际。另一种解析建模方法通过构建FPGA性能解析模型来对FPGA架构设计空间进行探索[69]-。解析建模方法手工推导FPGA架构性能关于架构参数的数学模型[1012]-。基于该性能模型并借助于几何规划，就可从设计空间中获得满足具体设计指标的优化架构。这种方法省时，而且推导出的性能模型是关于架构参数的显示模型，更加直观。然而，在模型推导过程中进行的一些简化和假设使得该性能模型不是十分精确和通用。此外，这种方法需要推导性能模型的设计人员对FPGA架构有非常全面的了解。

半监督模型树（Semi-supervised Model Tree, SMT）方法被提出以解决上述实验方法和解析建模方法中存在的问题[13]。首先，从设计空间中选出部分架构通过 VTR获得相应性能。然后采用半监督模型树算法学习表征这些架构的架构参数与相应性能之间的关系，而后自动建立关于架构参数的显示性能模型。获得的性能模型可预测设计空间中其他架构的性能。最后，结合非线性规划可从整体架构设计空间中获取优化架构。因为这种方法不需要将设计空间中的每一个架构通过VTR获得性能，所以SMT方法比实验方法更省时。同时，SMT方法是通过对基于VTR得到实际性能的FPGA架构进行学习来构建性能模型，因此它比解析建模方法更精确。然而SMT方法没有考虑实验电路信息。对于待学习的每一个架构，需要通过 VTR将实验电路集中的所有电路映射到这个架构上，对所有电路的性能结果取几何平均后作为这个架构的性能。这就导致了较长的建模时间。例如，要获得17个VTR实验电路在68个架构上的性能需要多达500 h[13]。此外，SMT方法只使用了 VTR电路集，如果实验电路集中加入新的电路时，就需要再运行 VTR获得新增的电路的性能来更新架构性能。

针对上述情况，本文提出一种基于电路特性的半监督建模方法。该方法能精确预测特定实验电路在指定架构上的实现性能，并加速FPGA性能建模过程，从而进一步加速FPGA设计空间探索过程。实验结果显示本文方法在预测FPGA实现面积和延时时预测精度分别高达6.25%和4.23%，与SMT方法的预测精度可比拟。同时，相较于SMT方法，建模时间可至少减半。此外，本文提出方法构建了一个通用的FPGA性能模型，当预测新的电路在新的FPGA架构上的实现性能时不需要再额外运行VTR。

2 FPGA性能建模框架

本文方法采用类似 SMT[7]方法机制来构建FPGA性能模型。然而，本文加入了电路相关特性作为先验知识使得构建的 FPGA性能模型更加通用。

图 1展示了本文方法的建模过程。首先，从FPGA架构设计空间中选择一些架构1A。然后，借助于VTR，将实验电路集中的部分电路1S分别映射到1A上。装箱、布局和布线之后，获得1S中每个电路在1A中每个架构上的实现性能（面积和延时）。以获得性能的架构和电路为基础，应用半监督模型树算法，开发未获得性能的架构2A和电路特性2S，构建一个关于架构参数和电路特性参数的FPGA性能模型。

表1简要呈现了上述建模过程中采用的改进的机器学习算法—半监督模型树算法[13]。该算法使用M5P[14]算法先对电路在特定架构上的实现性能进行学习构建初始性能模型，然后以半监督的方式对没有性能结果的架构和电路进行开发、学习，精炼模型。最终获得的性能模型可以预测新的电路在设计空间中其他架构上实现的性能。

3 FPGA性能模型参数选择

本文旨在通过构建FPGA实现面积和延时关于FPGA架构参数以及电路参数的模型进而探索FPGA架构设计空间。即采用FPGA架构参数和电路参数对FPGA实现面积和延时进行表征，以得到解析模型。基于该模型预测FPGA架构的性能，并研究模型参数对性能的影响，探索FPGA架构设计空间。本节主要介绍性能建模过程中采用的架构参数与电路特性参数。

图1 本文方法的建模框架

表1 半监督模型树算法伪代码

3.1 架构参数

目前主流的商用FPGA芯片都采用基于查找表的岛式结构[5]，本文以此为研究对象。如图2所示，基于查找表的FPGA主要架构参数包括查找表的输入数目（K），逻辑块中的查找表数目（N），逻辑块的输入数目（I），逻辑块的扇入系数（inFc ）和扇出系数（outFc ）。上述架构参数反映了FPGA的逻辑和互连结构，影响电路在FPGA上实现的面积和延时。K值越大，在一个K输入查找表中可以实现的逻辑功能越多，关键路径上的查找表数目减小，电路的延时越小，而同时K值的增大使得查找表的面积增大。N值的变化对面积与延时的影响效果与K值类似。I, N与inFc,outFc 联合作用影响逻辑块与其周围互连通道之间的通信能力。inFc与outFc 变大，逻辑块与通道的通信能力增强，与此同时却带来FPGA互连面积的增加。因此，要设计一个满足设计指标的FPGA架构，需要在上述架构参数之间进行折中选择。

3.2 电路特性参数

对于任一应用电路，可用5个基本电路参数来对其进行描述。这5个电路参数分别为实现电路需要的 2输入查找表的数目（n2），电路网表中触发器之间的最大门数（d2），电路的输入输出数目（nio），电路中触发器的数目（nDFF）以及线网数目（nnet）[9]。其中， n2,nio,nDFF和 nnet反映了应用电路的规模，而 d2,nDFF和 nnet则表征了应用电路的性能。本文基于VTR和MCNC两个实验电路集中的25个电路来探索上述电路参数与电路实现的面积和延时的关系。表2列出各个电路参数与电路面积和延时之间的相关系数。从表2可以看出 n2与面积之间相关系数最大，d2与延时最相关，而 nio对面积和延时的影响最小。此外， nnet与 nDFF也与面积密切相关，其与 n2之间的相关系数分别为0.9989, 0.7893，这说明nnet,nDFF与 n2不是相互独立的。因此，在本文提出的建模方法中，使用两个电路特性参数 n2和 d2来表征一个电路。

n2与 d2反映了电路的规模和时序信息。从这两个特性参数的定义上理解， n2的增大会使得电路面积增大，电路延时会随 d2的增加而增加。图3显示了VTR各电路中面积、延时随 n2, d2的变化趋势。

表2 各电路参数与面积和延时之间的相关系数

图2 FPGA架构示意图

图3 VTR电路中 2n,2d与面积、延时的变化关系

本文中FPGA性能模型涉及的参数，包括架构和电路特性参数总结在表3中。

表3 FPGA性能模型参数

4 实验及结果分析

本节通过实验来验证本文方法的精确性、时效性和通用性。

本文使用VTR和MCNC两个实验电路集中的电路进行相关实验。由于规模较大，VTR工具运行时间较长，两个最大的电路 LU32PEEng和 mcml被排除VTR实验电路集之外。MCNC实验电路集中的电路规模普遍较小，因此从中选择了8个最大的电路。使用ABC[15]来提取电路特性参数。表4列出了选用的17个VTR电路和8个MCNC电路的特性参数值。这些电路涵盖了不同领域的典型应用。本文采用VTR工具对电路在FPGA上实现的过程进行模拟，获得架构和电路对应的实现性能。

本文采用平均相对误差（Mean Relative Error,MRE）作为评估指标来评价本文方法的精确性。MRE定义见式（1）。其中， xi是通过 VTR获得的FPGA实现性能，而 x'i是通过本文方法获得的性能模型预测得到的性能。tN代表测试集中测试项的数目。

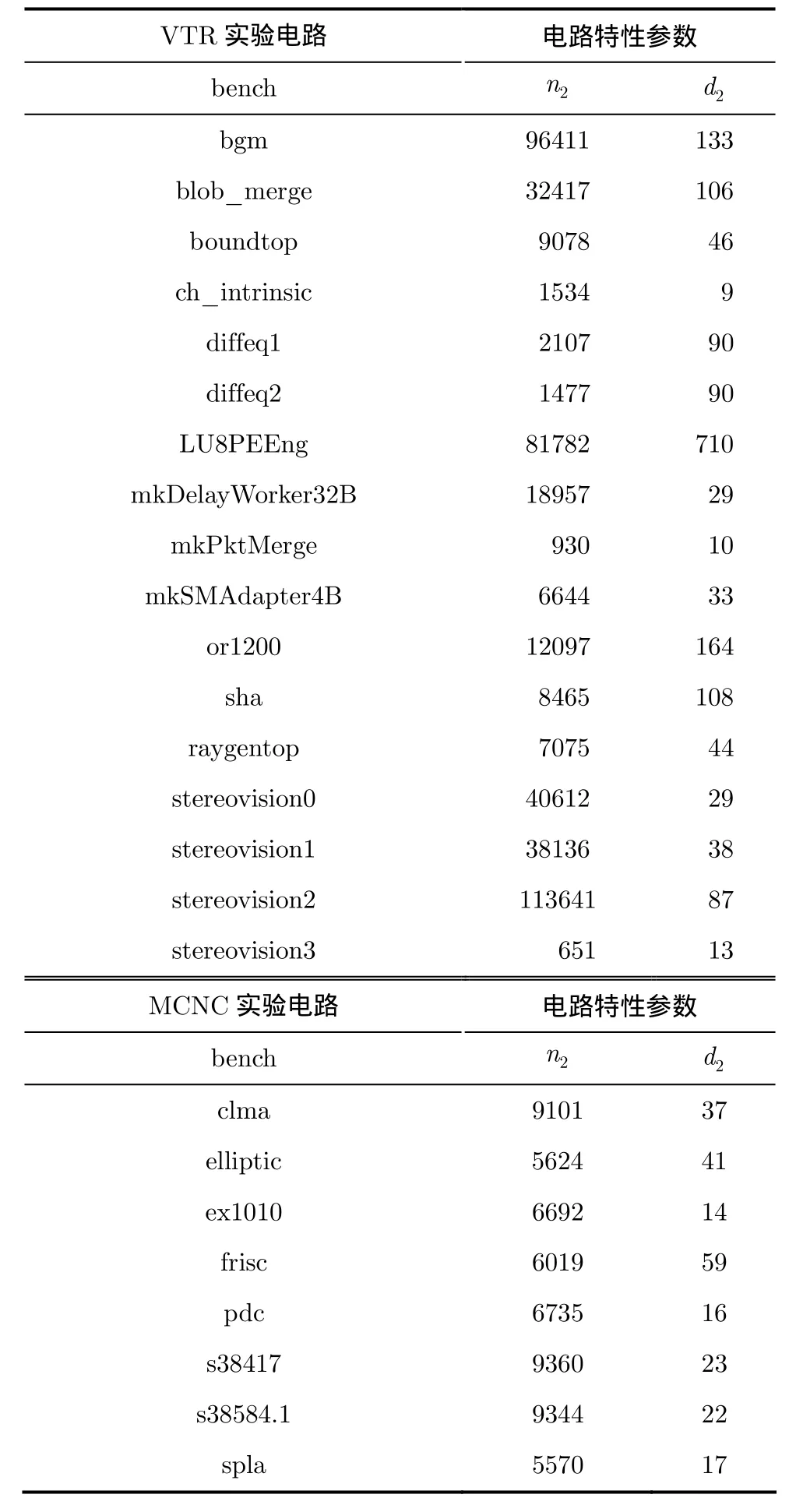
表4 VTR和MCNC电路特性参数

使用本文方法进行性能模型建模过程中，训练集的选择决定了最终生成的性能模型。为使模型更加精确和通用，训练集应该包含尽可能多的信息供学习算法进行学习。对于FPGA架构性能进行建模，训练集即为FPGA架构参数、电路特性参数和其相应的性能的数值组合。因此，训练集中FPGA架构参数和电路特性参数的数值选取应该具有代表性和多样性。以FPGA架构参数中的查找表输入数目K为例，K的取值范围为[4,10]，那么在选择训练集时，FPGA架构参数中K值的选取不应该集中于其取值范围中的某一区域，防止训练得到的性能模型只能预测该区域附近K值的性能值，而不能精确预测其他值。其他模型参数的数值选择也遵循此规则。

4.1 预测精度

本实验首先通过VTR获得了11个VTR电路在 6个 FPGA架构上的实现面积和延时作为训练集。基于该训练集使用本文方法学习FPGA实现面积和延时与其对应的电路特性和架构参数之间的关系。学习后构建的面积/延时模型用于预测测试集中另外6个VTR电路在2个新的FPGA架构上的实现性能。同时，通过 VTR获得测试集中电路的实现性能。针对测试集中的电路和架构组合，将本文方法构建模型预测的性能与通过 VTR获得的实现性能进行比较，计算两者之间的MRE，检验本文方法的预测精度。然后，减少训练集中本文方法学习的电路数目，观察预测MRE的变化。

图4展示了这一实验过程中MRE的变化过程。如图所示，学习11个VTR电路的性能得到的FPGA性能模型进行面积预测时MRE可达6.25%，延时预测时可达4.23%。SMT方法中不考虑电路特性（学习所有17个VTR电路的性能）预测面积和延时时的平均相对误差分别为5.96%和2.70%[13]。本文方法与文献[13]中方法预测精度可比拟。此外，当学习的实验电路数目从10个降到7个时，面积预测精度保持不变。并且当学习的电路数目从11个降到7个时，预测MRE仅从6.25%增长到7.80%。这说明通过使用本文方法可以减少学习的电路数目从而降低面积/延时模型建模过程的时间开销，同时仍保持一定的预测精度。从图4中还可以观察到当学习的实验电路数目从10降到9时，MRE减少。这是因为这个移除的电路与测试电路差异较大，学习这个电路的性能从而构建的性能模型会降低预测测试电路时的精度。当只学习3个电路的性能来构建面积/延时模型时，预测测试电路时的 MRE骤增，这说明学习的电路数目太少，不足以构建一个精确的性能模型。

4.2 时间开销

图4 MRE随学习的电路数目的变化趋势

利用半监督模型树算法进行FPGA性能建模的时间仅为1～5 min，探索FPGA架构设计空间的时间成本主要在于通过 VTR为学习算法提供带有性能结果的FPGA架构，如式（2）所示。

其中，n和m分别代表需要学习的架构和电路数目。总的时间成本tolT 为将m个电路在n个FPGA架构上通过VTR实现的时间之和。

文献[13]中方法在对 FPGA架构性能建模过程中没有考虑电路参数的影响，该算法需要将实验电路集中的所有电路在一个FPGA架构上实现，取电路性能的几何平均作为该FPGA架构的性能。因此，对于文献[13]中方法，时间成本中的 m为电路集的大小，并且文献[13]中方法不能预测某个指定电路在FPGA上的实现性能。而本文方法通过构建关于架构参数和电路参数的FPGA性能模型，可以预测特定电路在特定FPGA架构上的实现性能。

如表5所示，本文方法学习11个VTR电路（近似VTR电路集的2/3）构建面积/延时性能模型预测性能时与文献[13]学习所有17个VTR实验电路的建模方法预测性能的精度可比拟。学习7个电路（小于 1/2VTR电路集）性能构建的面积模型预测精度只降低到文献[13]中方法精度的92%。并且学习的电路数目从17减少到9个时，延时预测的精度几乎不变。

上述实验结果说明在保证预测精度的前提下，学习的电路数目可至少减半。因此，对于本文方法，时间成本中的 m为实验电路集的一半。文献[13]方法在Intel Xeon E7-4807上探索具有百万FPGA架构的设计空间时需要 500 h，采用本文方法仅需要250 h。此外，学习的实验电路数目可以进一步减少，这就需要在时间开销和预测精度之间进行折中选择。

表5 预测精度与时间开销随学习的电路数目的变化趋势

4.3 通用性

本文加入电路特性作为先验知识来构建FPGA性能模型，所以获得的性能模型能够精确预测新的电路的实现性能。这一节进行两组相关实验来验证本文方法的通用性。

在第1组实验中，基于训练集中2个VTR电路在8个架构上的实现性能，构建性能模型来预测测试集中另外一个VTR电路在相同8个架构上的实现性能。使用上述流程测试了预测每一个 VTR电路性能的预测精度。在第2组实验中，基于2个VTR电路在8个架构上的实现性能，构建性能模型来预测MCNC电路集中的电路在相同8个架构上的实现性能。

图 5显示了本文方法在预测 VTR（图 5（a））和MCNC（图 5（b））中每个电路时预测性能与实际性能之间的平均相对误差。可见，在预测 VTR电路的面积和延时时，除个别电路外，预测MRE在10%左右。然而在预测ch_intrinsics和stereovision3这两个电路的面积, 以及在预测 LU8PEEng和stereovision2这两个电路的延时时，预测结果不精确。如表 4所示，这是因为在 VTR电路集中stereovision3电路的2n值最小，stereovision2的2n最大。类似地，ch_intrinsics的2d是最小的而LU8PEEng的2d是最大的。这4个电路体现了VTR电路集中2n和2d特性参数的4个极端值，没有合适的电路去学习来表征这4个电路的性能。结果，获得的面积/延时模型对于这些电路来说不是足够精确。因此，为使最终的性能模型足够精确，所选取的待学习电路的特性需要有代表性。在用学习VTR电路性能构建的性能模型预测 MCNC电路的性能时，最大的平均相对误差不超过13%，证明了本文提出的基于电路特性的建模方法可以较好地预测新电路的性能，提供了一个通用的性能建模方法。

图5 预测来自不同电路集的电路性能时本文方法的MRE

4.4 电路特性对性能的影响

本文采用的半监督模型树算法最终生成一个关于FPGA架构和电路特性参数的显示性能模型。该模型能反映出电路特性对性能的影响趋势。

图 6为使用本文方法生成的面积（图 6（a））和延时（图6（b））性能模型示例。如图所示，面积模型中2n和延时模型中2d的系数均为正，说明在相同FPGA架构上（模型中FPGA架构参数相同时），面积和延时随电路参数2n和2d正比例增长，这与图3实验分析得到的趋势一致。因此，本文方法能对电路参数的影响进行良好的预测。

4.5 探索半监督模型树算法中的参数

在表1呈现的半监督模型树算法中，主要有两个参数1L和2L，代表了建模过程中两个模型树上叶端存在的最小样本数目。上述实验使用了这两个参数的经验值。本实验改变这两个参数的数值并观察MRE的变化。

图6 面积、延时模型树

表6呈现了变化的L 值对MRE的影响。可见，当这两个参数取相同值时，预测精度通常较差。因为两个模型树之间的相似性使得他们为彼此挑选相似的未标记样本。一旦挑选了一个不合适的样本，误差就会循环累积，最终导致一个不是十分精确的性能模型产生。此外，当两个参数数值都较小时，预测精度也不高。这是因为模型树叶端较少的样本数目使得性能模型过于精细，也就是说获得的性能模型在拟合训练样本时产生了过拟合的现象，这在一定程度上降低了预测测试样本的精度，尤其当测试样本与训练样本特性相差较大时。

5 结束语

本文呈现了一个电路特性驱动的FPGA架构性能半监督建模方法。该方法通过学习电路特性与实现性能之间的关系来构建FPGA性能模型。本文方法不需要获得所有应用电路在FPGA架构上的实现性能就可构建一个精确且通用的性能模型，加快了FPGA性能建模及架构设计探索过程。实验结果显示该方法能以6.25%的MRE预测FPGA性能，并可将具有百万架构的 FPGA设计空间探索时间由500 h降低为250 h。此外，本文方法不局限于只对基于LUT结构的FPGA性能进行建模，未来工作将对基于新型逻辑结构的FPGA性能建模，如基于与非锥结构的FPGA[16]。

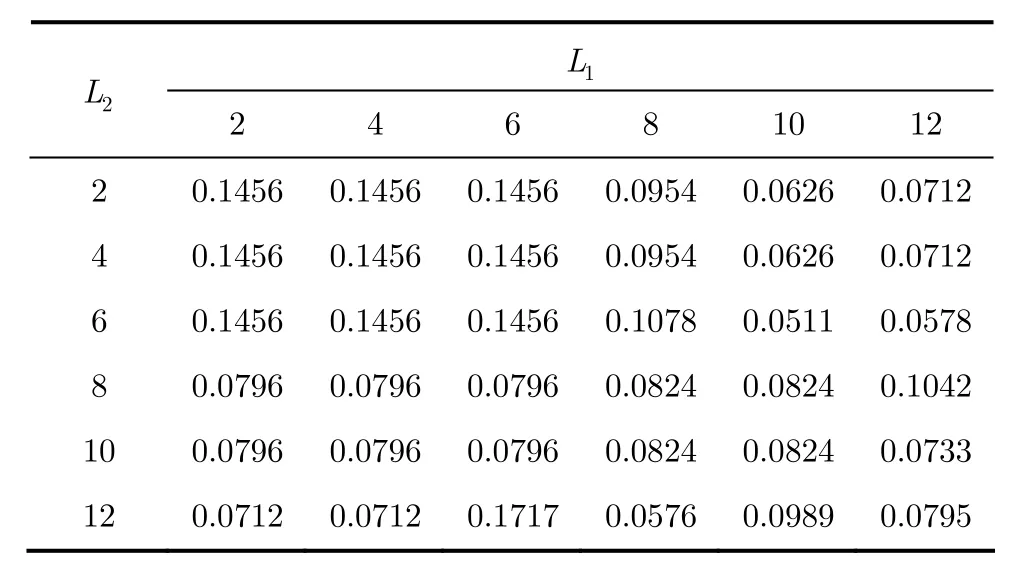
表6 L值对MRE的影响

[1] Luu J, Goeders J, Wainberg M, et al.. VTR 7.0: next generation architecture and CAD system for FPGAs[J].ACM Transactions on Reconfigurable Technology and Systems, 2014, 7（2）: 6:1-6:30.

[2] Marquardt A, Betz V, and Rose J. Speed and area tradeoffs in cluster-based FPGA architectures[J]. IEEE Transactions on Very Large Scale Integration （VLSI） Systems, 2000, 8（1）:84-93.

[3] Ahmed E and Rose J. The effect of LUT and cluster size on deep-submicron FPGA performance and density[J]. IEEE Transactions on Very Large Scale Integration （VLSI） Systems,2004, 12（3）: 288-298.

[4] Jiang Zheng-hong, Lin C Y, Yang Li-qun, et al.. Exploring architecture parameters for dual-output LUT based FPGAs[C]. Proceedings of the 24th International Conference on Field Programmable Logic and Applications, Munich,Germany, 2014: 1-6.

[5] Betz V, Rose J, and Marquardt A. Architecture and CAD for Deep-Submicron FPGAs [M]. Netherlands, Kluwer Academic Publishers, 1999: 15-20.

[6] Gao Hai-xia, Yang Yin-tang, Ma Xiao-hua, et al.. Analysis of the effect of LUT size on FPGA area and delay using theoretical derivations[C]. Proceedings of the 6th International Symposium on Quality of Electronic Design,San Jose, CA, USA, 2005: 370-374.

[7] Smith A, Wilton S, and Das J. Wirelength modeling for homogeneous and heterogeneous FPGA architectural development[C]. Proceedings of the 17th ACM/SIGDA international symposium on Field programmable gate arrays,Monterey, CA, USA, 2009: 181-190.

[8] Das J, Lam A, Wilton S, et al.. An analytical model relating FPGA architecture to logic density and depth[J]. IEEE Transactions on Very Large Scale Integration （VLSI） Systems,2011, 19（12）: 2229-2242.

[9] Smith A, Constantinides G, and Cheung P. FPGA architecture optimization using geometric programming[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2010, 29（8）: 1163-1176.

[10] Pandurangaiah Y, Reddy V, and Chakravarthy K.Area-delay estimation by concurrent optimization of FPGA architecture parameters using geometric programming[J].International Journal of Computer Applications, 2013, 82（18）:4-11.

[11] Mehri H and Alizadeh B. An analytical dynamic and leakage power model for FPGAs[C]. Proceedings of the 22nd Iranian Conference on Electrical Engineering （ICEE）, Tehran, 2014:300-305.

[12] Leow Yoon-kah. Post-routing analytical models for homogeneous FPGA architectures[D]. [Ph. D. dissertation],The University of Arizona, 2013.

[13] Yang Li-qun, Yang Hai-gang, Li Wei, et al.. A semi-supervised modeling approach for performance characterization of FPGA architectures[C]. Proceedings of the 24th International Conference on Field Programmable Logic and Applications, Munich, Germany, 2014: 1-6.

[14] Wang Y and Witten I H. Inducing model trees for continuous classes[C]. Proceedings of the Ninth European Conference on Machine Learning, Prague, Czech Republic, 1997: 128-137.

[15] Brayton R and Mishchenko A. ABC: an academic industrial-strength verification tool[J]. Computer Aided Verification, 2010, 6174: 24-40.

[16] Zgheib G, Yang Li-qun, Huang Zhi-hong, et al.. Revisiting and-inverter cones[C]. Proceedings of the 2014 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 2014: 45-54.