一种用于测试数据压缩的自适应EFDR编码方法

邝继顺 周颖波 蔡 烁



一种用于测试数据压缩的自适应EFDR编码方法

邝继顺 周颖波*蔡 烁

(湖南大学信息科学与工程学院 长沙 410082)

该文提出一种用于测试数据压缩的自适应EFDR(Extended Frequency-Directed Run-length)编码方法。该方法以EFDR编码为基础，增加了一个用于表示后缀与前缀编码长度差值的参数，对测试集中的每个测试向量，根据其游程分布情况，选择最合适的值进行编码，提高了编码效率。在解码方面，编码后的码字经过简单的数学运算即可恢复得到原测试数据的游程长度，且不同值下的编码码字均可使用相同的解码电路来解码，因此解码电路具有较小的硬件开销。对ISCAS-89部分标准电路的实验结果表明，该方法的平均压缩率达到69.87%，较原EFDR编码方法提高了4.07%。

测试数据压缩；EFDR(Extended Frequency-Directed Run-length)编码；自适应EFDR编码；解码

1 引言

测试成本的迅速增长是目前集成电路设计制造中的一个主要问题。一方面，随着特征尺寸的减小，集成电路中所包含的IP核与集成的逻辑门数量增多，使得所需测试数据规模增大；而另一方面，自动测试仪(ATE)的工作频率、I/O通道数目、传输带宽、存储能力却增长有限。两者之间的矛盾是导致测试时间增加，测试成本上升的主要原因[1]。

对测试数据进行压缩是一种能有效解决该矛盾的方法。目前测试数据压缩方法主要分为3类：基于线性解压结构的压缩方法、基于广播扫描的压缩方法和基于编码的压缩方法[2]。其中编码压缩方法主要针对给定测试集，将测试集中的测试数据分割成多个符号(字符串)，再将每个符号用一个新码字替代，形成压缩后的数据，存储在ATE中。编码压缩方法主要分为两类，其中一类是基于游程的编码方法，它的基本原理是对原始测试数据中连续的0或1的长度(称作游程)进行编码，包括FDR编码[3]，EFDR(Extended Frequency-Directed Run-length)编码[4]，多维游程编码(MD-PRC)[5]，交替变游程编码(AVR)[6]，对称游程编码(SVC)[7]和一位标识混合编码[8]等；另一类是基于数据块的编码方法，它是将原始数据划分为定长或变长的数据块，根据不同数据块的出现频率进行编码，对高频率的数据块赋予较短的码字。这类编码包括可变长Huffman编码(VIHC)[9]，块合并编码(BM)[10]，四值稀疏存储编码[11]等。此外近年来人们也提出了一些适用于多扫描链结构[12,13]和用于降低测试功耗[14,15]的编码压缩方法。编码压缩不需要了解被测电路的内部结构信息，也不需要进行故障模拟或测试产生，非常适用于嵌入有IP核电路的测试数据压缩[1]。

目前基于游程的编码压缩方法大都是根据整个测试集的游程分布情况提出的，没有考虑到在测试集的不同测试向量之间，游程分布存在着巨大差异。本文以此为切入点，提出一种自适应EFDR编码方法，以EFDR编码为基础，增加了一个用于表示后缀与前缀编码长度差值的参数，对测试集中的不同测试向量，用不同的值进行编码，有效提高了测试数据压缩率。

2 EFDR编码

EFDR编码是一种重要的基于游程的编码压缩方法。EFDR编码被称之为FDR编码[3]的扩展码，在FDR编码的基础上增加了一位标识位，0表示对0游程编码，1表示对1游程编码。由于可同时对两种游程编码，因此经过对无关位Ｘ的适当填充，EFDR 编码的游程总数会远远小于仅基于0 游程的FDR编码，其压缩率也比FDR编码有较大提高。EFDR的完整编码由标识位加前缀加后缀组成，其编码表在表1中给出。

表1 EFDR编码表

然而EFDR编码自身也存在一些缺陷，制约了它编码压缩率的提高：

EFDR编码对测试集中的所有测试向量均使用相同的编码方法，而没有考虑到不同测试向量的游程分布存在巨大差异。表2为Mintest测试集中测试向量的无关位X比例表，列出了各电路测试集的测试向量中包含X位比例的最低值、最高值和平均值。由表2中可以看出，最低值与最高值之间差异显著，这使得各测试向量的游程分布也大为不同[1]。以电路s9234为例，X位比例的最低值仅为4.86%，对应的测试向量中绝大部分位都是确定位，游程分布以短游程为主，若用EFDR进行编码，则编码后的数据量反而大于原始数据，起不到压缩的效果；而X位比例的最高值则为95.14%，此时对应的测试向量中绝大部分位都是无关位，游程分布以长游程为主(X填充后，最短游程长度为14位)，而EFDR编码中，却将大量编码码字用于对短游程编码(由表1可知，长度为1~6的游程，占用了前缀为0和10的编码码字)，这造成了编码资源的极大浪费。因此对这些游程分布差异很大的测试向量单一使用EFDR编码并不合适。

表2 MinTest测试集中X位比例

3 自适应EFDR编码

针对上一节中EFDR编码的缺陷，本文提出了一种用于测试数据压缩的自适应EFDR(Adaptive EFDR, A-EFDR)编码方法，在原EFDR编码的基础上，增加了一个用于表示后缀与前缀编码长度差值的参数。对测试集中的每个测试向量，根据其游程分布情况，选择最合适的值进行编码。表3和表4列出了其中和时A-EFDR编码的编码表，其余值下的A-EFDR编码表可依类似方法得出(其中的编码表即为表1)。

表3 A-EFDR编码表(N=-1)

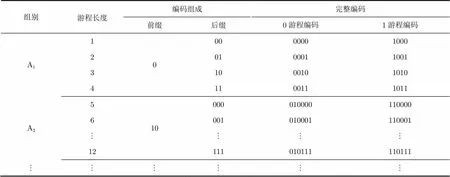
表4 A-EFDR编码表(N=1)

与EFDR编码类似，A-EFDR编码也采用由标识位加前缀再加后缀组成。标识位用于区分是对0游程编码还是对1游程编码；前缀与EFDR编码中前缀相同，对于不同组别A(=1,2,3,)，前缀编码由个1和一个0构成；后缀长度则不再固定与前缀长度相同，而是相差一个值。因为前缀的起始长度为1位，而后缀起始长度必须大于等于0，所以参数的取值范围为：。A-EFDR编码表中，起始的游程长度为1位，对应的起始编码长度为位，同一组别的游程编码长度不变，跨组别的相邻游程编码长度增量为2；每一个组别A中，包含的游程长度个数为个。

给出一个A-EFDR编码的实例。

原始测试数据：TD=000000111110 0000000001 (22位)

编码后数据：

=0时，TE=01011 11001 0110010 (17位)

=1时，TE=010001 1011 010100 (16位)

可以看出，对于相同的测试数据，不同值的A-EFDR编码对应的编码长度各不相同，我们选取使编码长度最短的值进行编码，这里选取=1。

对比上一节提到的EFDR编码中的缺陷。EFDR编码中，前后缀长度相等，值固定为0，对测试集中所有测试向量都使用同一种编码方法；而在A-EFDR编码中，值大小可变，可根据测试向量中游程的分布选取最合适的进行编码。当测试向量中X位比例较低，游程分布以短游程为主时，可选取较小的值，值减小，则编码表中游程的起始编码长度减小，有利于对短游程的编码；而当测试向量中X位比例较高，长游程比例增加时，可选取较大的值，值增大，虽然编码表中游程的起始编码长度增加，但每一个组别中包含的不同游程长度个数呈指数增长，仍有利于对长游程的编码。A-EFDR编码增加了编码方法的灵活性，根据游程的分布，优化了编码字的长度，有效避免了EFDR编码中的缺陷。

4 压缩增益分析

我们从概率论的角度来计算压缩增益。根据A-EFDR编码规则，设参数大小为，则组别A包含的游程范围为，对应的码字长度为2++1。

设测试数据中某一位为0的概率为，则为1的概率为，其中。则长度为的0游程出现概率为，长度为的1游程出现概率为。由此可得，对于某一游程，其属于组别A的概率为

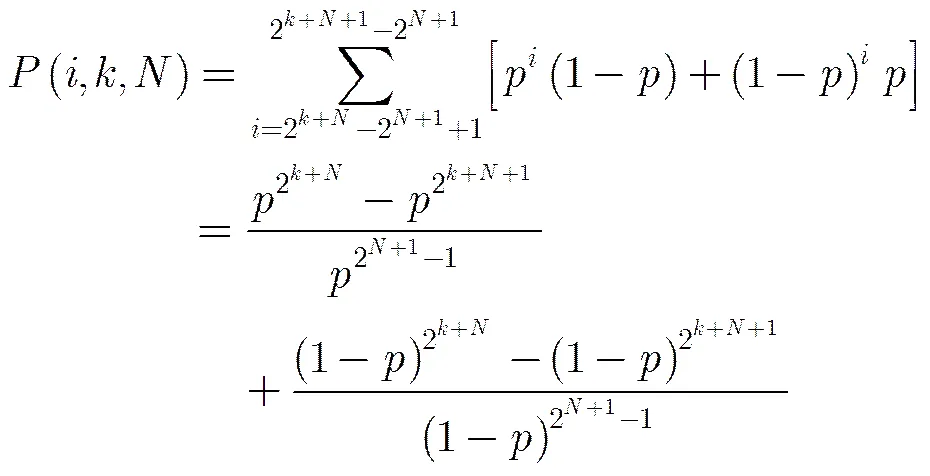
组别A对应的码字长度为2++1。因此A-EFDR编码的平均编码长度为

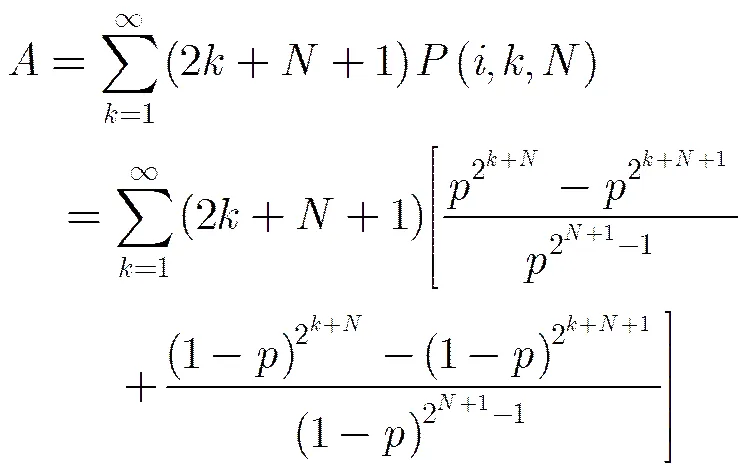
而原始数据中的平均游程长度为

因此得到A-EFDR编码的压缩增益为

取=0，即可得到EFDR编码的压缩增益为

为了更直观比较不同值下A-EFDR编码的压缩增益，我们通过Matlab画出了其中取值为-1, 0, 1时A-EFDR编码的压缩增益曲线，如图1所示。纵轴表示压缩增益，横轴为每一位取0的概率。因增益曲线关于=0.5轴对称，所以这里只给出了区间中的曲线进行分析。从图中可以看出，不同值的A-EFDR编码有各自优势的值区间，且值越小，优势的区间越靠近=0.5。在时，压缩增益最高；时，=0压缩增益最高；＞0.88时，=1压缩增益最高。实际上，随着的增大，值也需要增加才能取得更高的压缩增益，如＞0.92时，=2比=1的压缩增益更高。因此我们可以根据测试向量中值的大小，选取对应压缩增益最高的值进行编码，提高编码压缩率。

图1 不同N值下A-EFDR编码压缩增益图

5 解码器设计

一个优秀的编码压缩方法，在保持较高数据压缩率的同时，还应当具有较小的硬件解码开销[1]。对经过A-EFDR编码压缩的码字经过简单的数学运算即可解码，且不同值的A-EFDR编码均可使用相同的解码电路来解码。

设测试数据游程长度为，编码参数为，编码后码字的前缀大小为1，后缀大小为2，则与,1,2之间的数学关系表达式为

以=1时的A-EFDR编码为例，设前缀1= (10)2，后缀2=(111)2，则游程长度为：位，表达式前缀1乘以2，对应于解码器中是将前缀1左移位的操作，不同值的A-EFDR编码对应移位的长度不同。在电路中实现移位操作较为简单，所需的硬件代价较小。

图2为A-EFDR编码方案解码电路框图。其结构由一个有限状态机(FSM)、一个位计数器、一个log2位计数器、一个位计数器、一个位寄存器和一个异或门组成。其中位计数器用于读取编码中的前缀和后缀；log2位计数器记录前缀和后缀的长度；位寄存器和位计数器分别存储当前编码的参数和对应的测试向量数目；标识位flag通过异或门控制当前解码数据的游程种类。与EFDR解码电路[4]相比，本解码电路仅增加了一个位计数器和一个位寄存器，增加的硬件开销相对较小。

该解码电路解码步骤如下：

(1)读入信息控制位部分：信号en置为高电平,接收bit_in中的数据，将当前编码参数和对应的向量数目分别存入位寄存器和位计数器中。

(2)读入标识位部分：接收bit_in的一位数据，赋值给flag信号。

(3)读入前缀部分：bit_in中的数据读入位计数器，直到接收到0为止(接收到0表示前缀部分读入完毕，这里0读取但不存入计数器中)；log2计数器记录前缀的位数。之后读取位寄存器中的参数，将位计数器中数值左移位，log2计数器中数值增加。

(4)前缀部分解压：FSM输出0至data,输出高电平，表示输出有效。FSM每输出一个0,位计数器减1，直到位计数器为空，rs1为1，前缀部分解压结束。

(5)读入后缀部分：bit_in中的数据接着读入位计数器，每读入一位数据log2位计数器减1，直到log2位计数器为空，rs3为1，后缀部分读入结束。

(6)后缀部分解压：与前缀解压部分类似，FSM输出0至data，输出0的个数为位计数器的数值，之后再输出一个1，游程解压完毕。

(7)若一个测试向量解压完毕，位计数器减1。当计数器数值为0时，转入步骤(1)，重新读入控制信息位；否则转入步骤(2)，开始新游程的解码。

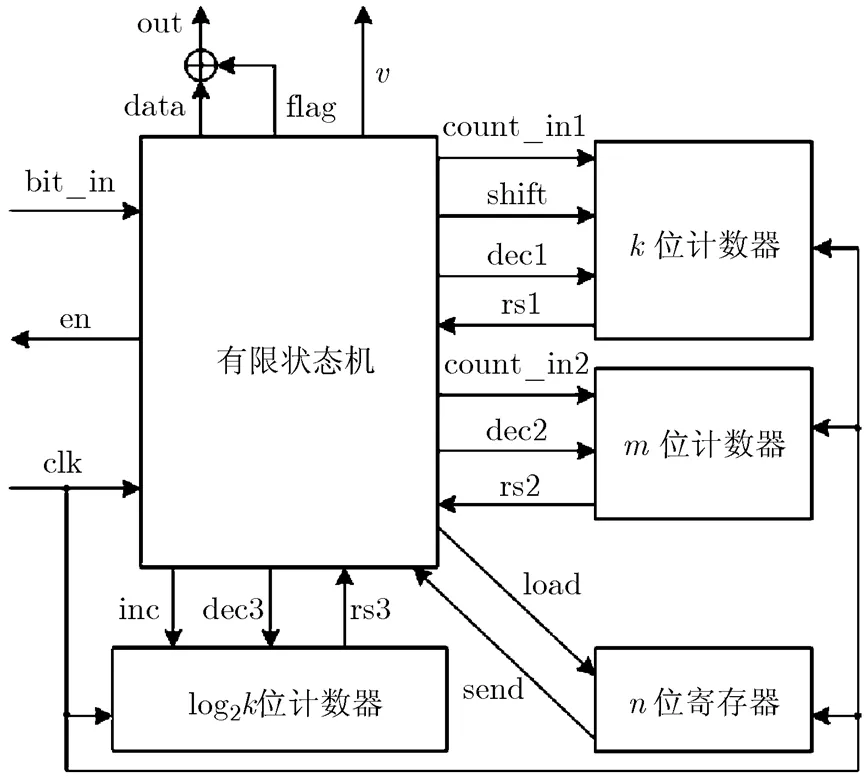
图2 解码电路框图

6 实验结果与分析

为了验证A-EFDR编码的压缩效果，本文以Mintest故障测试集为对象，对ISCAS-89 标准电路中最大的几个电路进行了实验。

在A-EFDR编码中，需要对测试集中不同测试向量选取各自最合适的值进行编码。本文中对每个测试向量用不同的值进行了尝试，选取对应最合适的那个，得到的值分布表如表5所示，表中任意值对应的列，表示选取相应值的测试向量个数，最后一列为测试向量数目总和。之后每个测试集中的测试向量按对应值的大小进行了重排序。

从表中可以看出，值的大小分布在-1~7之间，不同测试集的值范围各不相同。其中电路s5378和s38417的值最高值都比较小，这是因为这两个电路的高Ｘ位比例的测试向量中，确定位并非均匀分布，而是集中出现的，这使得测试向量中仍存在相当比例的短游程，导致对应的值比较小。

表5 N值分布表

由第5节提到的解码过程可知，A-EFDR编码与EFDR编码相比，需要额外存储一些控制信息位，包括当前编码参数，以及值对应的测试向量数目。表6为控制信息位表，列出了各个测试集中原始测试数据的位数，和所需额外存储的控制信息位数。信息位计算方法以电路s9234为例：由表5可知，s9234的测试集被分为了8个子集，每个子集需要提供一次对应的值和测试向量数目。值最大为6，需要用3位表示；而不同值下，最大测试向量个数为42(时)，需要用6位表示，因此s9234总共所需存储的控制信息位位数为：位。

从表6中可以看出，各个测试集中所需存储的控制信息位都很小，最大不超过100位，对比于Mintest测试集中原始测试数据的位数，所占比例极小，因而对测试数据的压缩不会有太大影响。

表7为本方法与目前国内外主流的编码压缩方法在压缩率[3]方面的比较，其中第2列到第5列为基于游程的编码压缩方法，分别为EFDR编码[4]，多维游程编码(MD-PRC)[5]，交替变游程编码(AVR)[6]和对称游程编码(SVC)[7]；第6第7列为基于数据块的编码压缩方法，分别为块合并编码(BM)[10]和四值稀疏存储编码[11]；最后一列为本文提出的A-EFDR编码。以上编码压缩方法都是选用的相同的测试集，且都没有进行向量差分或扫描链重排序等操作。本文A-EFDR编码方法中，对无关位X的填充，采用文献[16]中提出的动态最优填充算法。

表6控制信息位表

电路名称测试数据位数控制信息位数占比(%) s5378 23754320.13 s9234 39273720.18 s13207165200990.06 s15850 76986640.08 s35932 28208240.08 s38417164736360.02 s38584199104720.04

从表７中可以看出，与EFDR编码相比，本文方法对每个电路测试集的压缩率都有提高，平均提高了4.07%，这也说明了本方法对EFDR编码中缺陷的改进是有效果的。7个电路中，电路s35932在压缩率已经很高(80.80%)的基础上继续提高了4.27%，这主要是因为s35932测试集中确定位0和1并非均匀分布，而是“抱团”出现，测试集中含有大量的连续0和连续1，形成了许多长游程，使得每个测试向量对应的值都比较高(参见表5)，因而压缩率较值固定为0的EFDR编码有较大提高。

表7本方法压缩效果与其他压缩方法的比较(%)

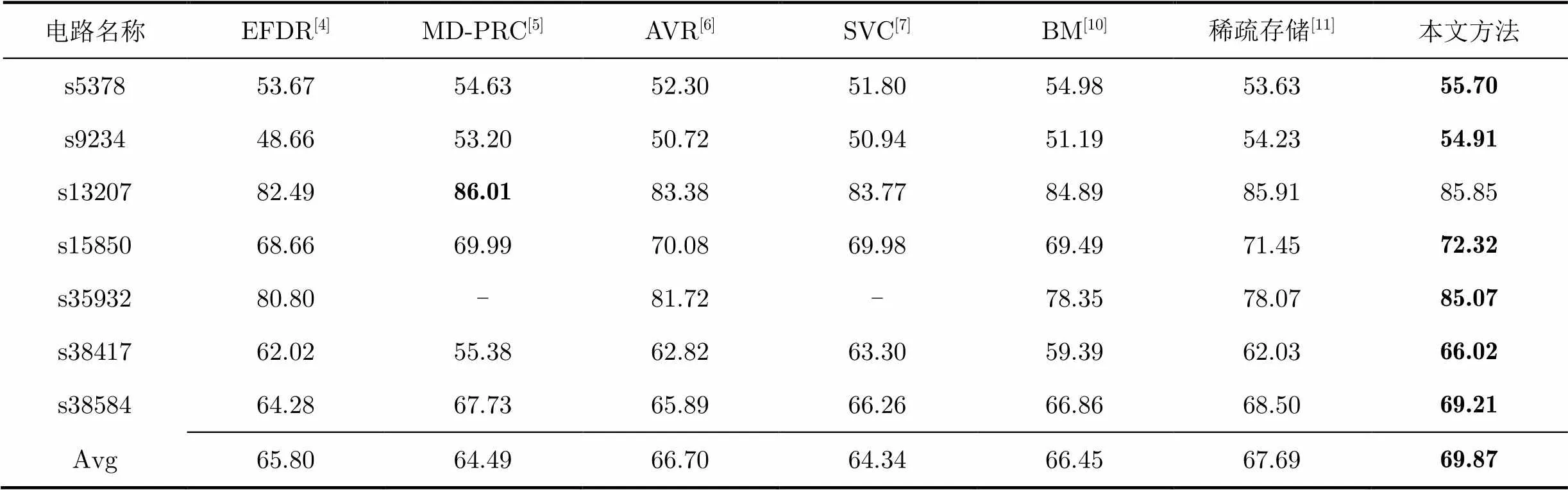
电路名称EFDR[4]MD-PRC[5]AVR[6]SVC[7]BM[10]稀疏存储[11]本文方法 s537853.6754.6352.3051.8054.9853.6355.70 s923448.6653.2050.7250.9451.1954.2354.91 s1320782.4986.0183.3883.7784.8985.9185.85 s1585068.6669.9970.0869.9869.4971.4572.32 s3593280.80-81.72-78.3578.0785.07 s3841762.0255.3862.8263.3059.3962.0366.02 s3858464.2867.7365.8966.2666.8668.5069.21 Avg65.8064.4966.7064.3466.4567.6969.87

对比表中的其他国内外参考文献，除s13207电路外，本文方法的压缩效果都是最优的，且本文方法还有解码电路简单的优势，这些数据也充分说明了本编码压缩方法的有效性。

7 结论

针对测试集中不同测试向量的游程分布存在巨大差异的特点，本文提出了一种自适应EFDR编码的测试数据压缩方法。本文方法以EFDR编码为基础，增加了一个用于表示后缀与前缀编码长度差值的参数，对测试集中的不同测试向量，选用不同的值进行编码，有效提高了测试数据压缩率。在解码方面，本方法较EFDR编码仅需增加少量硬件资源，硬件解码开销仍然较低。综上所述，本文方法具有较好的应用前景。

[1] Mehta U S, Dasgupta K S, and Evashrayee N J. Un-length-based test data compression techniques: how far from entropy and power bounds a survey[J]., 2010(1): 1-9.

[2] 刘铁桥, 邝继顺, 蔡烁. 一种将测试集嵌入到Test-per-Clock位流中的方法[J]. 计算机研究与发展, 2014, 51(9): 2022-2029.

Liu Tie-qiao, Kuang Ji-shun, and Cai Shuo. A new method of embedding test patterns into test-per-clock bit stream[J]., 2014, 51(9): 2022-2029.

[3] Anshuman C and Krishnendu C. Frequency-Directed Run- length(FDR) codes with application to system-on-a-chip test data compression[C]. Proceedings of the 19th IEEE VLSI Test Symposium, Atlantic, 2001: 42-47.

[4] EL-Maleh A H. Test data compression for system-on-a-chip using Extended Frequency-Directed Run-Length Code[J].&, 2008(2): 155-163.

[5] Dauh T W and Jen L L. Test data compression using multi-dimensional pattern run-length codes[J]., 2010, 26(3): 393-400.

[6] Ye B, Zhao Q, Zhou D,.. Test data compression using alternating variable run-length code[J].,, 2011(44): 103-110.

[7] 梁华国, 蒋翠云, 罗强. 应用对称编码的测试数据压缩方法[J]. 计算机研究与发展, 2011, 48(12): 2391-2399.

Liang Hua-guo, Jiang Cui-yun, and Luo Qiang. Test data compression and decompression using symmetry-variable codes[J]., 2011, 48(12): 2391-2399.

[8] 马会, 邝继顺, 马伟. 基于一位标识的测试向量混合编码压缩方法[J]. 电子测量与仪器学报, 2013, 27(4): 312-318.

Ma Hui, Kuang Ji-shun, and Ma Wei. Hybrid coding compression method of test vector based on an identification [J]., 2013, 27(4): 312-318.

[9] Gonciari P T, AI-Hashimi B M, and Nicolici N. Variable- length input Huffman coding for system-on-a-chip test[J]., 2003, 22(6): 783-789.

[10] EL-Maleh A H. Efficient test compression technique based on block merging[J].&, 2008, 5(2): 327-335.

[11] Zhang L and Kuang J S. Test data compression using selective sparse storage[J]., 2011, 27(4): 565-577.

[12] 刘杰, 易茂祥, 朱勇. 采用字典词条衍生模式的测试数据压缩[J]. 电子与信息学报, 2012, 34(1): 231-235.

Liu Jie, Yi Mao-xiang, and Zhu Yong. Test data compression using entry derivative mode of dictionary[J].&, 2012, 34(1): 231-235.

[13] Sismanoglou P and Nikolos D. Test data compression based on reuse and bit-flipping of parts of dictionary entries[C]. Proceedings of 17th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Warsaw, 2014: 110-115.

[14] Tyszer J, Filipek M, Mrugalski G,.. New test compression scheme based on low power BIST[C]. Processdings of 18th IEEE European Test Symposium, Avignon, 2013: 1-6.

[15] Chloupek M, Jenicek J, Novak O,.. Test pattern decompression in parallel scan chain architecture[C]. Proceedings of 16th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Karlovy, 2013: 219-223.

[16] 方昊, 姚博, 宋晓笛. 双游程编码的无关位填充算法[J]. 电子学报, 2009, 37(1): 1-7.

Fang Hao, Yao Bo, and Song Xiao-di. The algorithm of filling X bits in dual-run-length coding[J]., 2009, 37(1): 1-7.

Adaptive EFDR Coding Method for Test Data Compression

Kuang Ji-shun Zhou Ying-bo Cai Shuo

(&,,410082,)

An adaptive Extended Frequency-Directed Run-length (EFDR) code method for test data compression is presented in this paper. The method is based on EFDR code, and adds an additional parameter, which is used to represent the code length difference between tail and prefix. According to the distribution of the runs in each test vector of the test set, the method selects the most suitablevalues to code, and it can improve the compression ratio. For the decompression, according to the size of the codeword, the run length of the original test data can be obtained with a simple mathematical operation. Meanwhile, those codeword under different parameter values can be decoded by the same decompression circuit. Thus, the decompression circuit can keep in a low hardware cost level. The experimental result shows that the average compression rate of the proposed method can achieve to 69.87%, over 4.07% than original EFDR code method.

Test data compression; Extended Frequency-Directed Run-length (EFDR) code; Adaptive EFDR code; decode

TP302

A

1009-5896(2015)10-2529-07

10.11999/JEIT150177

2015-02-02；改回日期：2015-05-21；

2015-07-06

周颖波 zhoubobo@163.com

国家自然科学基金(61472123, 60673085)

The National Natural Science Foundation of China (61472123, 60673085)

邝继顺： 男，1959年生，博士，教授，研究方向为集成电路测试与设计，嵌入式系统.

周颖波： 男，1984年生，博士生，研究方向为集成电路测试.

蔡 烁： 男，1982年生，博士生，研究方向为集成电路测试.