一种用于压缩感知理论的投影矩阵优化算法
2015-12-13吴光文张爱军王昌明
吴光文 张爱军 王昌明
1 引言
文献[1~3]在 2006年提出了压缩感知理论(Compressed Sensing, CS)。该理论指出,对于稀疏信号,可以通过少量的观测数据恢复原信号,且观测数据的量远小于传统的香农-奈奎斯特采样定理规定的最小数据量,该理论使得高分辨率信号的采样能够突破当前硬件速度限制,实现高速采样和数据压缩。
自然界中的多数信号具有一定的规律性,这种规律性体现在数学形式上就是:用一组特定的基底表示信号时,变换系数是稀疏的(绝大多数的系数为零或者绝对值非常小)。稀疏性是CS的理论基础,利用信号稀疏性,构造 CS系统包括两个步骤:设计感知机构(编码机构)和选取合适的重构方法(解码机构)[4]。精确信号重构(解码)所需要的数据量依赖于感知矩阵与稀疏字典之间的相关性和信号自身的稀疏度[5],而投影矩阵的性能是决定编码质量的关键。作为 CS理论研究的一个重要方向,现有的文献对投影矩阵的约束条件进行了研究,这些约束条件主要包括约束等距性质,零空间性质和相关系数[611]-。然而,判断投影矩阵是否具备约束等距性质和零空间性质是组合复杂度问题,实际用于投影矩阵性能分析非常困难[12]。
文献[13,14]引入了相关系数的概念,在CS理论中,相关系数的含义是指投影矩阵与稀疏字典之间列向量内积的最大值,其物理意义是两者最差相似性[6]。文献[6~10]的研究表明,通过减少投影矩阵与稀疏字典的相关系数可以提高 CS的重构性能,即相关系数越小,精确重构信号所需的观测值数目越少,信号适应的稀疏度范围越大。
文献[6]提出了一种阈值平均系数方法表示投影矩阵与稀疏字典的相关性,并通过线性收缩 Gram矩阵中绝对值大于限定阈值的非对角元的方法迭代减小相关系数,取得了较好的实验效果。但是,该方法的计算过程只有收缩系数非常接近1时才近似凸函数[6]。而当线性收缩系数近似为1时,收缩速度非常慢。另外,该算法在使用处理过的Gram矩阵计算降阶投影矩阵时会产生干扰,产生绝对值较大的相关系数[4],本文4.1节的实验结果表明该算法产生的相关系数比较大,甚至比优化前更大。文献[7]用等角紧框架 (Equiangular Tight Frame, ETF)Welch界作为投影矩阵和稀疏字典相关系数的极限最小值,将ETF作为优化目标建立一个变形的凸集合,使用梯度下降法逼近最优凸集合中的矩阵,计算投影矩阵。相对于文献[6]算法,此算法更稳定,但是在算法中步长因子β要根据经验确定,β的选择对算法影响比较大[4]。
本文对投影矩阵与稀疏字典的相关性进行研究,优化产生具有最小相关性的投影矩阵,提高信号重构的精度并降低编码机构对信号稀疏度的要求。设计连续可导的阈值函数,对Gram矩阵的非对角元进行收缩处理。使用基于沃尔夫条件的梯度下降法迭代逼近最优投影矩阵,提高算法的稳定度。
2 压缩感知的基本理论
CS理论定义[4]:假设信号 x ∈Rn在一组字典Ψ =(Ψ1,Ψ2, …,Ψn)上具有s( s < <n)稀疏度,通过其在投影矩阵 Φ = ( φ1, φ2, …,φn) 上的 m ( m ≥s) 个线性观测值y ( i)= x, φi,i ∈ { 1,2,… ,m }能够获得精确重构的过程,即

式中,Φ为投影矩阵,Ψ为稀疏字典,y为观测值。
由于信号是稀疏的且信号恢复为病态求逆过程,信号重建可以理解为寻找最小0l范数解的过程。初始信号的稀疏表示向量0α满足:
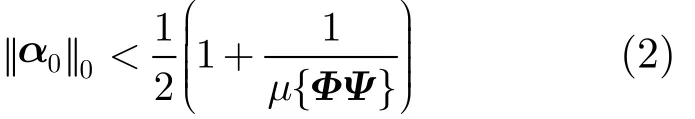
选定投影矩阵Φ,信号的重构问题转化为求解式(3),使用重构算法(如BP, OMP)能够计算出重构信号的稀疏表示α,进而重构原始信号x[6]:
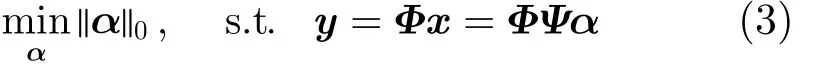
由式(2),投影矩阵和稀疏字典的相关性为信号准确重建提供保证,相关系数越小,精确重构信号所需的观测值数目越少,或者说适应信号的稀疏度范围越大。投影矩阵和稀疏字典的相关系数定义为[6]

其中D是感知矩阵,理论上说,相关系数{}μ D越小,感知(编码)原始信号后蕴含的信息量越多,但是相关系数有一个下界,即Welch界,如式(5)所示。
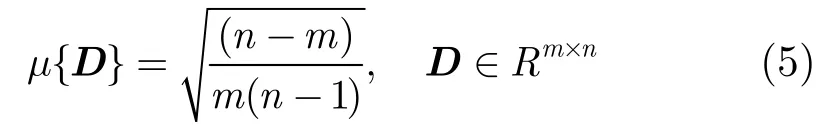
3 投影矩阵的优化算法
3.1 感知矩阵相关系数

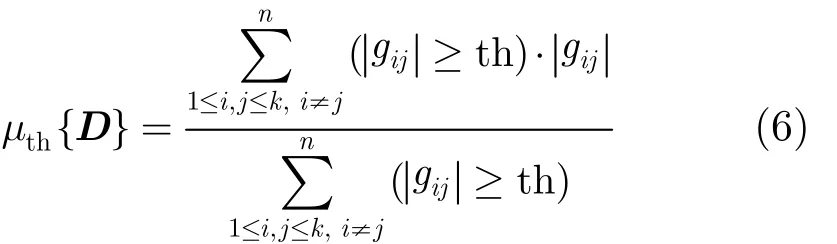
式中,th[0,1)∈为阈值,式(6)的含义为绝对值大于等于阈值th的G矩阵的非对角元的绝对平均值,能较好地评价投影矩阵的总体相关性。
3.2 Gram矩阵的阈值函数
应用阈值函数处理投影矩阵与稀疏字典生成的Gram 矩阵非对角元,可以使其逼近最优目标。因此,阈值函数对投影矩阵的优化过程起到关键作用,文献[6]中所用的线性优化方法,只有当线性收缩系数γ非常接近1时,才能保证优化过程是收敛的。本文提出一种阈值函数,此函数在单极性区间为凸函数,在(-1,1)区间连续且可导,能够在保证收敛速度的情况下尽量保留原始数据特征。

式(7)中有两个参数,th和m, th选恒定值且须th≥ μwelch, μwelch为Welch界。另外式(7)满足

式(8)表明,式(7)不仅在阈值±th处连续,而且可导。m为大于1的可变参数,当m由小变大时,函数的压缩程度变大,不同m值对应的函数如图 1所示。图1中,th = 0 .2,当m值越大,原始数据的特征改变越大,整体迭代算法的速度越快;m值越小,原始数据的特征改变越少,整体迭代算法的速度越慢,稳定性越好。
图2显示了不同m取值时迭代收缩1000步对应的阈值平均相关系数的曲线,稀疏字典为200×400的随机矩阵,原始的投影矩阵为30×200的高斯分布的随机矩阵 Φ ,阈值选择 t h =0.2 ≥ μwelch=0.1758。m取值分别为1.4, 2.0, 8.0。从图2中发现,3个m取值对应的曲线都收敛,且随着m值变大收敛速度变快。大量实验表明,m在区间[1,+∞)中取其它值时,函数曲线变换趋势和图2类似。
3.3 更新投影矩阵
优化投影矩阵需要在每个迭代步骤中从收缩非对角元的Gram矩阵中解算出对应的投影矩阵Φ。文献[6]先用Cholesky分解Gram矩阵,再用Moore-Penrose逆求投影矩阵,此方法会引入干扰误差,产生较大的相关系数。文献[7]提出梯度逼近法求解投影矩阵Φ,运算的精度高,算法更加稳定。但是文献[7]的方法受迭代步长的影响,本文引入基于沃尔夫条件的梯度下降法,用快速逼近每次迭代过程产生的Gram矩阵的方法计算投影矩阵Φ。

式中,kG 为第k步迭代收缩后的Gram矩阵,用梯度下降法由kΦ计算1k+Φ。定义函数,
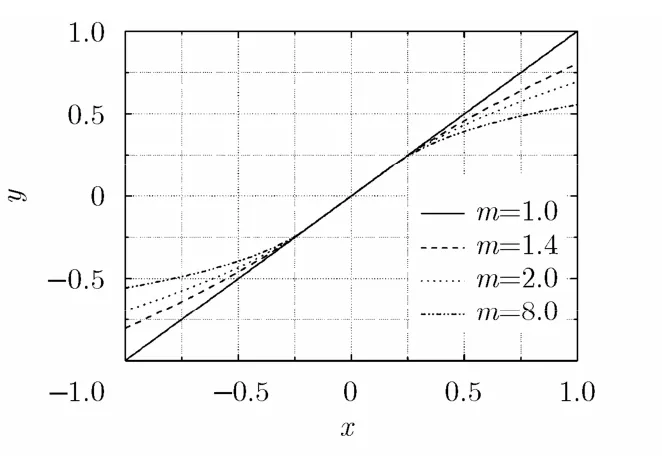
图1 Gram矩阵的阈值函数

根据文献[15],

为了区别于梯度下降法中迭代过程的标识,将式(11)简写作 ∇ J = 4 Φ Ψ ( ΨTΦTΦ Ψ -)ΨT,梯度下降法的迭代步骤为
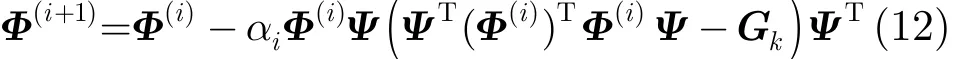
其中迭代运算的初始值 Φ(0)=Φk,当式(9)迭代运算达到精度要求时,令=Φ(i+1), i为梯度下降法迭代的步数。计算式(12)的一个关键步骤是求解步长αi,文献[7]已经证实J(Φk) 并非简单的二次函数。因此,一些简单的确定迭代步长的方法在这里不适用。引入文献[16]提出的基于沃尔夫条件的梯度下降法来解决这个问题。梯度下降法求极值的迭代过程的实质就是保证式(13)成立,
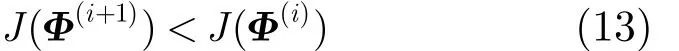
保证式(13)成立的一个实用的规则是沃尔夫条件:
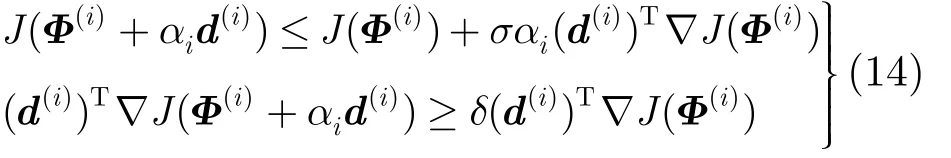
式 (14)中 , 0 < σ < δ < 1 为 给 定 的 常 数 ,(d(i))T∇ J(Φ(i)) 为函数J( Φ) 在d(i)方向上的方向导数。式(14)的第1个不等式叫做Armijo规则,该规则的数学含义是:步长αi越大,函数J( Φ)的值改变越大。式(14)的第2个条件的含义是:J( Φ)在点上的方向导数的值必须大于等于δ倍的初始值 Φ(i)的导数值。
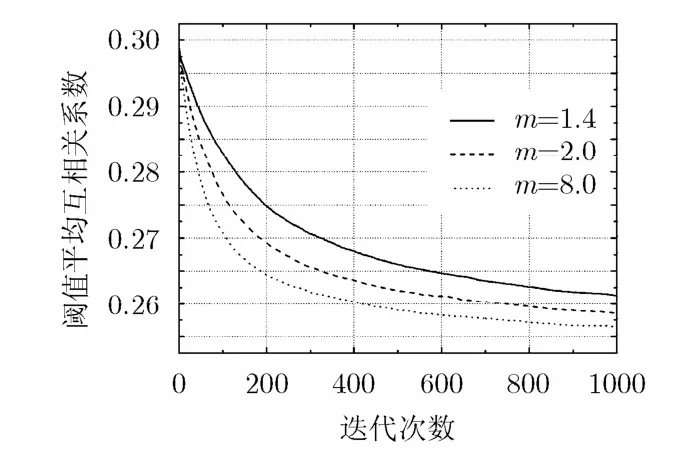
图2 阈值平均相关系数
在实用中σ取值应非常小,但δ要取大值[16],本文取值 σ =10-4, δ=0.9,使用回溯算法确定符合沃尔夫条件的迭代步长αi,算法如图3所示。
根据图3所示算法求得迭代步长αi,将步长代入式(12)即可用梯度下降法求得满足最小误差的Φ(i+1),此即优化后的投影矩阵Φ 。投影矩阵优化
k+1算法分为两大步,第1步更新Gram矩阵,第2步更新投影矩阵。将这两步细化后的具体的步骤如图4所示。迭代次数Iter可以是确定的数值,还有另一种方法控制迭代结束,就是判断连续两次相关系数之间的差值,如果差值小于设定的值,结束迭代过程。

图3 回溯算法求步长流程图
3.4 算法分析
收敛性分析 沃尔夫条件是对梯度下降法中线性搜索方向和步长的限制条件,在式(14)第 1个不等式中,α 为步长,(d(i))T∇ J (Φ(i)) 为方向导数,这
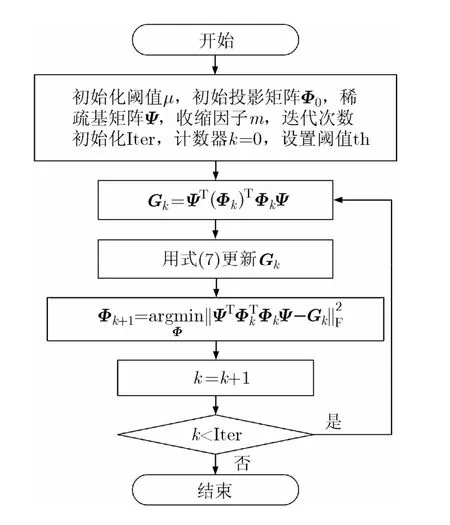
图4 投影矩阵优化流程
i个不等式保证函数J的下降幅度与步长αi和方向导数 (d(i))T∇ J (Φ(i)) 这两个量是比例关系,即保证每次迭代下降足够大的量,此式又称作阿米贺条件(Armijo condition)。式(14)中的第 2 个不等式是曲率条件,保证目标函数在步长αi处的斜率是(d(i))T∇ J (Φ(i)) 的 δ倍。只要满足沃尔夫条件,算法的收敛性就会满足,即沃尔夫条件是梯度下降算法有效性的充分条件,文献[17]给出了满足沃尔夫条件的步长αi的存在性证明。
算法时间复杂度 本文用计算机浮点数运算的次数表示算法的时间复杂度。假设投影矩阵Φ为N×M矩阵,Ψ为M×M矩阵,则Gram矩阵计算中 , 浮 点 运 算 的 次 数 为 M2(2N - 1 )+ 2M N(2M- 1 );更新Gram矩阵的运算中,使用式(7)对非对角元素压缩,在选定阈值函数后,,(m - 1 )th是常数,每个非对角元的压缩需要执行两次乘法运算,一次开方运算和一次减法运算,此处Gram矩阵为M×M矩阵,但对角元素不参与运算,所以浮点数运算的最大次数是 4 (M2- M ),此时对应所有非对角元全大于阈值th的情况;更新投影矩阵的迭代运算中,假设梯度下降法的迭代步数为K,浮点数运算的次数为 1 2K M2N - 3 KMN。算法时间复杂度可以表示为: I (12K M2N - 3 K MN + 3M2+ 6 M2N - 4 M - 2 M N), I = I ter 是算法的总体迭代次数。
算法性能边界 使用本文提出的Gram矩阵非对角元收缩算法对投影矩阵进行优化时,投影矩阵不会产生大量的零值元素,重构算法的适用种类比较多。相关实验表明,该算法可以配合常用的重构算法对信号压缩感知处理,如 BP算法,匹配追踪(Match Pursuit, MP)算法,OMP算法,压缩采样匹配追踪(Compressive Sampling Matching Pursuit,CoSaMP)算法,正则化正交匹配追踪(Regularized Orthogonal Matching Puisuit, ROMP)算法等,均可以重构优化投影矩阵观测的原始信号。
4 仿真实验
为了验证本文算法的有效性,选择高斯分布的随机矩阵作为原始投影矩阵,分别使用文献[6]方法、文献[7]方法和本文方法优化原始投影矩阵,然后用这3种优化的投影矩阵和原始的投影矩阵分别进行实验。首先考察各种投影矩阵的相关系数,进而用各种投影矩阵压缩感知稀疏向量、1维和2维信号,考察不同投影矩阵对应的重构信号误差情况。
4.1 优化相关系数实验
选择初始投影矩阵Φ为30×200的高斯分布随机矩阵,Ψ为200×400的稀疏字典。文献[6]优化方法选择:阈值th = 0 .2,收缩因子 γ : γ1=0.55,γ2= 0 .75,γ3= 0 .95,迭代1000次;文献[7]方法选择:th = 0 .2,迭代次数100,每次迭代过程中求最佳观测矩阵的迭代次数 50,迭代步长 β : β1=0.01,β2= 0 .02;本文方法选择:th = 0 .2, σ = 0 .0001,δ= 0 .9,收缩系数 m = 2 ,迭代次数为Iter = 1 00,求最佳观测矩阵的迭代次数为50。实验结果为各种算法迭代结束后相关系数μmax和大于设定阈值的相关系数平均值μav,如表1所示。
表1中的实验结果表明,各种算法优化原始投影矩阵后,大于设定阈值的相关系数平均值μav都有不同程度的下降,说明这3种优化算法都能够实现降低平均相关性的目的。其中经文献[6]方法优化投影矩阵后,μmax相对其它两种优化方法偏大,在γ1=0.55时甚至比原始投影矩阵的μmax更大。即用文献[6]方法优化投影矩阵后,代表相关性的参数μmax在某些情况下变大了,而非变小。本文在γ取值在 0.50~0.99之间,以不同的步长改变γ的值,做了大量的实验,实验结果表明,当0.50 ≤ γ ≤0.70时,μmax比优化前的值大;当0.75≤ γ ≤ 0 .95时,μmax比优化前的值小,且随着γ变大而μmax逐渐变大;产生这种现象的原因主要是在处理的Gram矩阵计算降阶投影矩阵时产生了干扰,因而产生了绝对值较大的相关系数。如果将文献[6]方法优化的投影矩阵用在信号处理中,信号处理的总体效果变好,因为μav变小了;但是有少数的局部成分会比优化前更差,因为μmax比较大。文献[7]方法优化投影矩阵后,μmax和μav都有较大的下降,体现了较好的性能,如果将文献[7]方法优化的投影矩阵用在信号处理中,处理的总体效果和局部效果都比原始投影矩阵好。但是,当迭代步长β取不同值时,对μmax和μav的影响较大,实际应用中,使用者需要根据经验和实际信号的特征选择最佳迭代步长,且计算过程中容易陷入局部最优的情况而找不到全局最优值。和其他方法比较,本文提出的优化算法在迭代步数相同、运算量不增加的情况下,maxμ和avμ的值最小,优化的效果最好。
4.2 随机稀疏向量实验
为了验证投影矩阵优化算法在整个压缩感知过程中的有效性,使用确定稀疏度的稀疏向量作为原始信号。先使用感知矩阵对原始信号编码产生观测信号,再使用BP算法和OMP算法对观测信号进行重构,根据重构的误差验证编码的效果,进而检验投影矩阵的性能。实验选取100000个长度是120,稀疏度是 4的向量(非零值随机分布),稀疏字典为80120×的单位随机矩阵,观测值n取区间[16,40]内的偶数,原始投影矩阵为 n×80的高斯分布随机矩阵,另外原始投影矩阵分别经过文中提到的3种方法优化,共4种投影矩阵用于实验,选择迭代次数为1000次。纵坐标为重构误差的对数表示,实验所用的一部分代码来自SparseLab工具箱[18]。结果如图5所示。
图5中的曲线变化趋势表明,随观测值增加,4种投影矩阵对应信号重构误差逐渐减小。比较图5(a)4种投影矩阵对应的曲线,3种优化后的投影矩阵对应的效果均优于原始投影矩阵,说明这3种优化方法对投影矩阵的性能具有改善作用。而本文方法的效果比其它算法效果更好。图 5(b)中的曲线变化趋势同图 5(a),说明了本文方法相对于其它算法的优势不受重构算法的影响。

表1 不同投影矩阵对应的相关系数
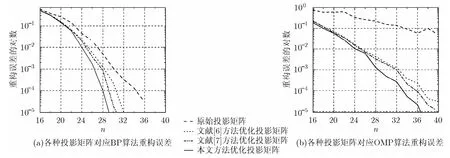
图5 4种投影矩阵对应重构误差随观测值n变化曲线
4.3 信号仿真实验
使用不同投影矩阵对1维和2维信号分别进行压缩感知实验,对观测值使用 OMP算法重构,比较各种算法的优化效果。1维信号选择 blocks,Doppler信号,均使用小波变换稀疏原始信号。其中 blocks信号用 haar小波,Doppler信号用Symmlet8小波。比较重构信号,本文方法优化的投影矩阵对应的重构信号最逼近原始信号。其中,重构的Doppler信号如图6所示,因blocks信号的重构效果图可以得出同样的结论,这里省略。
用信噪比和均方根误差两项指标对不同算法进行比较,如表 2,表 3所示。从表中看出,相对于其它投影矩阵,使用本文的方法对投影矩阵优化后,重构信号的信噪比最高,均方根误差最小。
选择大小为256×256的Lenna灰度图像,首先使用离散 Symmlet8小波对原始图像进行稀疏化处理,再使用不同投影矩阵进行压缩感知处理,最后进行图像重建,不同的投影矩阵处理的结果如图7和表4所示。2维信号处理的结果同样表明本文算法相对于其它优化算法有较大的优越性。
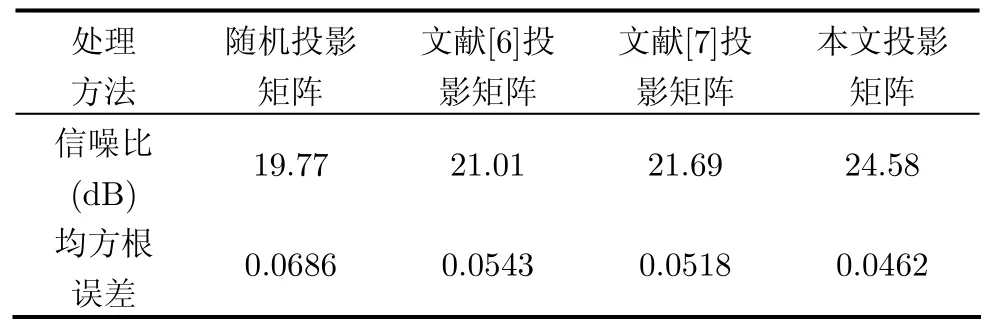
表2 不同投影矩阵对应的重构blocks信号指标
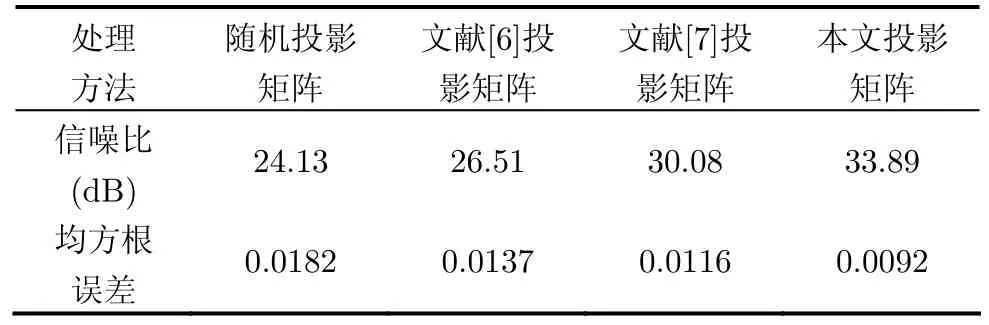
表3 不同投影矩阵对应的重构doppler信号指标

表4 不同投影矩阵对应的重构Lenna图像指标
5 结束语
本文对压缩感知投影矩阵的优化问题进行了研究,提出了连续可导的收缩阈值函数,保证了收缩Gram 矩阵非对角元的迭代过程的收敛性。用梯度下降法逼近投影矩阵的方法提高了优化过程中投影矩阵算法的精度和稳定性,克服了用Moore-Penrose逆来求解投影矩阵产生的干扰误差问题。使用基于沃尔夫条件的梯度下降法,解决了迭代步长对算法性能影响较大的问题。通过对随机稀疏向量使用各种投影矩阵的压缩感知实验,考查使用BP和OMP算法重构信号时产生的误差,证明了本文所提算法在提高信号重构性能的优越性。通过对基本的小波测试信号和图像进行压缩感知处理,使用 OMP算法对感知后的信号进行重构,实验结果表明本文的算法在压缩感知处理实际信号时,优于实验中的其它算法。本文的研究工作还有许多有待改进的地方,例如如何优化收缩阈值函数的数学表达式,以构造相关性更小的投影矩阵;研究如何实现投影矩阵优化和感知信号重构的协同问题。

图6 不同投影矩阵对应的重构Doppler信号

图7 不同投影矩阵对应的重构Lenna图像
[1] Donoho D L, Elad M, and Temlyakov V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006,52(1): 6-18.
[2] Candes E J, Romberg J K, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics, 2006,59(8): 1207-1223
[3] Candes E J and Tao T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12):5406-5425.
[4] 郑红, 李振. 压缩感知理论投影矩阵优化方法综述[J]. 数据采集与处理, 2014, 52(1): 43-53.Zheng Hong and Li Zhen. Survey on optimization methods for projection matrix in compress sensing theory[J]. Journal of Data Acquisition and Processing, 2014, 52(1): 43-53.
[5] 戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报,2011, 34(3): 425-434.Dai Qiong-hai, Fu Chang-jun, and Ji Xiang-yang. Research on compressed sensing[J]. Chinese Journal of Computers,2011, 34(3): 425-434.
[6] Elad M. Optimized projections for compressed sensing[J].IEEE Transactions on Signal Processing, 2007, 55(12):5695-5703.
[7] Abolghasemi V, Ferdowsi S, and Sanei S. A gradient-based alternating minimization approach for optimization of the measurement matrix in compressive sensing[J]. Signal Processing, 2012, 92(3): 999-1009.
[8] 李佳, 王强, 沈毅, 等. 压缩感知中测量矩阵与重建算法的协同构造[J]. 电子学报, 2013, 41(1): 29-34.Li Jia, Wang Qiang, Shen Yi, et al.. Collaborative construction of measurement matrix and reconstruction algorithm in compressive sensing[J]. Acta Electronica Sinica,2013, 41(1): 29-34.
[9] Zhang Qi-heng, Fu Yu-li, Li Hai-feng, et al.. Optimized projection matrix for compressed sensing[J]. Circuit System Signal Processing, 2014, 33(5): 1627-1636.
[10] Xu Jian-ping, Pi Yi-ming, and Cao Zong-jie. Optimized projection matrix for compressive sensing[J]. EURASIP Journal on Advances in Signal Processing, 2010,doi:10.1155/2010/560349.
[11] 林波, 张增辉, 朱炬波. 基于压缩感知的 DOA估计稀疏化模型与性能分析[J]. 电子与信息学报, 2014, 36(3): 589-594.Lin Bo, Zhang Zeng-hui, and Zhu Ju-bo. Sparsity model and performance analysis of DOA estimation with compressive sensing[J]. Journal of Electronics & Information Technology,2014, 36(3): 589-594.
[12] Donoho D L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797-829.
[13] Donoho D L and Stark P B. Uncertainty principles and signal recovery[J]. SIAM Journal on Applied Mathematics, 1989,49(3): 906-931.
[14] Donoho D L and Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via minimization[J].Proceedings of the National Academy of Science, 2003, 100(5):2197-2202.
[15] Petersen K B and Pedersen M S. The matrix cookbook[OL].http://www.matrixcookbook.com, 2013.10.
[16] Barth T J, Griebel M, Keyes D E, et al.. Scientific computing with MATLAB and octave[OL]. http://www.springer.com/series/5151, 2013.12.
[17] Jorge N and Wright S J. Numerical Optimization Theoretical and Practical Aspects[M]. 2nd Edition, New York: Springer-Verlag Berlin and Heidelberg GmbH & Co. K, 2006: 30-60.
[18] Stodden V and Donoho D. SparseLab21-core[OL]. http://sparselab.stanford.edu, 2013.10.
