一种基于逆序广义2近邻的图像多重复制粘贴篡改检测算法

李 岩 刘 念 张 斌 袁开国 杨义先

1 引言

随着计算机和网络技术的发展，数字图像篡改问题日益严重。被篡改后的数字图像所携带的错误信息有可能对公众舆论产生错误的导向。数字图像取证技术不依靠任何事先嵌入的数字水印或数字签名就可以对图像的完整性进行鉴别，该技术已经成为图像处理领域的一个重要研究课题和研究热点[18]-。

复制粘贴是一种很常见的数字图像篡改手段。近年来，有许多关于复制粘贴篡改检测的论文发表[13]-。复制粘贴篡改检测大致可以分为两类：基于块的检测方法[9,10]和基于特征点的检测方法[1114]-。这些文献中提出的方法可以很好地解决复制粘贴篡改检测问题，但却没有提到如何解决多重复制粘贴篡改问题。

广义 2近邻（generalized 2 Nearest-Neighbor,g2NN）算法[15]是一种可以解决多重复制粘贴篡改检测的算法。但经本文实验发现，如果图像中有某块区域被复制后在多处地方粘贴，那么g2NN算法的检测结果中有可能会遗漏某些复制粘贴区域。

本文研究数字图像的多重复制粘贴篡改检测技术，在g2NN算法的基础上，对其进行改进，提出逆序广义 2近邻（Reversed generalized 2 Nearest-Neighbor, Rg2NN）算法，弥补了g2NN算法的缺点，可以检测到所有复制粘贴区域，提高了检测准确率。在本文中，首先对图像进行加速鲁棒特征[16]（Speeded Up Robust Features, SURF）提取，然后使用优先（Best Bin First, BBF）算法[17]对每个特征点计算近邻，并使用 Rg2NN算法对特征点进行匹配，借鉴文献[18]的方法，对复制粘贴区域的特征点进行划分，通过匹配特征点之间的仿射变换关系，计算出复制粘贴的区域轮廓。

2 特征匹配算法

在使用特征点匹配方法进行复制粘贴篡改检测的文献中，提取图像的特征点后，需要对特征点进行匹配，根据特征点的匹配情况，计算出对应的复制粘贴区域。

2.1 g2NN算法

2.2 Rg2NN算法

本文认为g2NN算法存在如下缺点：假设特征点 xa和特征点 xb的距离为 dab，特征点 xa和特征点xc的距离为 dac。当特征点 xb和特征点 xc都和特征点 xa匹配时， dab和 dac都很小，但 dab和 dac的比值dab/dac有可能较大（大于 Tg2NN）。这时，若使用g2NN算法，就会认为特征点 xb和特征点 xc都不和特征点xa匹配。

本文对g2NN算法做出如下改进并提出Rg2NN算法。

（1）在Rg2NN算法中，逆序计算特征点距离之间的比值，即依次计算n-1,… , 2 ） ， 若Rg2NN， 且Tk-1＜ TRg2NN，那么待检测点和距其 { d1, d2,… , dk-2}的k- 2 个特征点均相似。

（2）计算和特征点 xi相匹配的特征点时，只和特征点 { xi+1,xi+2,… , xn}进行计算。因为 { x1, x2,… ,xi-1}在之前已经计算过。避免计算得到 xi和 xj相匹配后，又得到 xj和 xi相匹配的重复结果。

（3）在 Npix像素范围之外计算匹配特征点[19]。避免距离较近的点由于相似的纹理导致特征点相似。

在待检测图像中，假设源区域O被复制后分别粘贴于 D1,D2和 D3，每块区域中分别有特征点 x0,x1, x2和 x3，如图1所示。特征描述符之间的欧几里德距离及相邻距离的比值如表 1所示。使用Rg2NN算法，逆向计算相邻距离的比值，当计算到时，认为特征点 x1,x2和 x3均和特征点 x0匹配。而使用g2NN算法，计算得到因此仅认为 x1和 x0匹配，忽略了 x2,x3和 x0的匹配关系。由此可见，使用Rg2NN算法可以准确计算出全部匹配特征点，而g2NN算法会漏掉某些特征点之间的匹配关系。

图1 Rg2NN特征点匹配示例

3 基于Rg2NN的图像多重复制粘贴篡改检测

本文提出一种用于检测数字图像多重复制粘贴篡改的算法。算法总共分为4步：

（1）特征提取。给定待检测图像，使用特征提取算法计算待检测图像中的特征点。

（2）特征匹配。计算每个特征点的近邻，并使用Rg2NN算法从近邻特征点计算匹配特征点。

（3）特征点区域划分。根据匹配特征点之间的仿射变换关系对特征点的区域进行划分。

（4）多重复制粘贴区域定位。计算每块复制粘贴区域的轮廓，把所有区域轮廓叠加，得到检测结果。

表1 特征点之间的距离

在以下各小节中，将对算法的4个步骤进行详细阐述。

3.1 特征提取算法

文献[20]提出的尺度不变特征变换（Scale Invariant Feature Transform, SIFT）算法在计算机视觉领域应用广泛。文献[16]提出 SURF算法，在各方面性能（比如可重复性、区分性、鲁棒性等）都接近甚至超过SIFT，而且在运算速度上比SIFT更胜一筹。本文选用SURF特征检测算法。

3.2 Rg2NN特征匹配算法

使用BBF算法对所有特征点计算近邻后，在特征匹配阶段，使用 Rg2NN算法。如上文所述，Rg2NN算法比g2NN算法计算出来的匹配特征点更加准确，能够避免g2NN算法对匹配特征点的遗漏情况。

3.3 特征点区域划分

文献[15]提出一种只考虑特征点的坐标，而不考虑特征点匹配关系的区域划分算法。其缺点有2个：（1）不能区分距离较近的复制粘贴区域，（2）不能区分特征点分布不均匀的复制粘贴区域。为了解决该问题，文献[18]提出一种基于杰卡德距离连接[21]（Jaccard distance Linkage, J-Linkage）的算法，把拥有同样仿射变换的特征点归为一类。

3.4 多重复制粘贴区域定位

假设有n对匹配的复制粘贴区域，分别计算各对区域之间的仿射变换矩阵 {T1, T2,… ,Tn}。把Ti及其逆矩阵作用于待检测图像 Io，得到前向仿射变换图像 If和后向仿射变换图像 Ib。使用零均值归一化互相关（Zero mean Normalized Cross-Correlation, ZNCC）算法分别计算 Io和 If, Ib的相关性[18]。去除高斯白噪声后，用阈值 TBW把结果二值化，去掉面积小于图像面积 Asmall的孤立区域，最后使用数学形态学[22]方法连通区域，去除空洞。对每个 Ti进行上述计算，把所有结果叠加，得到复制粘贴区域定位结果。

4 实验结果与分析

本文提出的算法在Matlab R2012上进行实验，运行环境为个人PC机，CPU主频2.2 GHz，内存4 GB。实验中使用的参数如表2所示。参数阈值的选择将在第4.3节进行实验分析。

4.1 测试图库集

本文实验使用的测试图库集以 I N R I A Copydays dataset[23]为基础，对图像进行多重复制粘贴篡改。在原始图像中选择一块或几块任意形状、任意尺寸的区域，复制后，在图像中进行一次或多次粘贴。为了使篡改区域和原始区域更好地融合，可以把篡改区域缩放 0.8～1.2倍，旋转 0～180°之间的任意角度，并模糊边缘。将 INRIA Copydays dataset中的157张图像进行上述处理后，生成157张多重复制粘贴篡改图像。

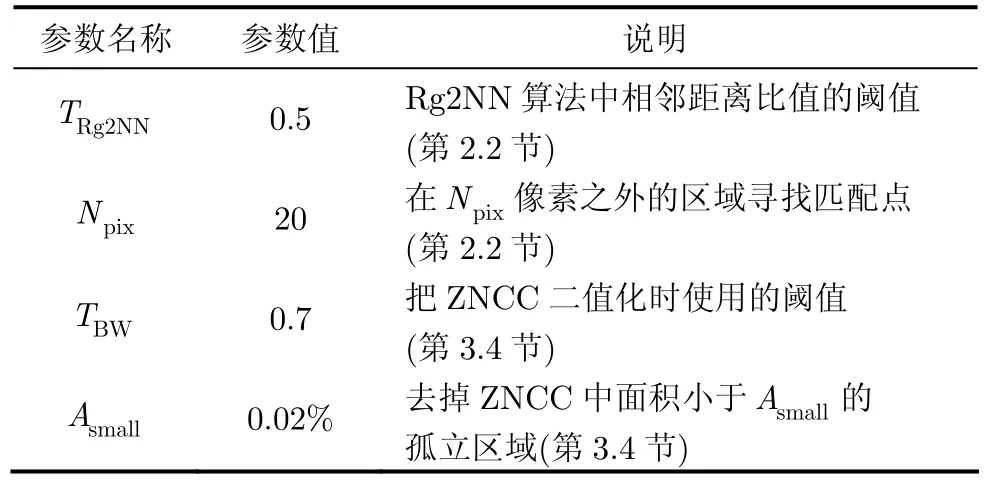
表2 实验中使用的参数

本文测试图库集中的示例图像如图2所示。其中，图 2（a）和图 2（d）分别为 INRIA Copydays dataset中文件名为201300和207000的未被篡改的图像，图 2（b）和图 2（e）分别为其经过复制粘贴篡改的图像，图 2（c）和图 2（f）分别为被篡改图像的复制粘贴区域显示。多重复制粘贴篡改有两种情况：（1）多块区域分别被复制后粘贴到其他多个地方，如图2（c）所示。（2）一块区域被复制后被粘贴到多个地方，如图2（f）所示。把201300图像的A0区域复制后，竖直向下位移305像素，水平向左位移468像素，缩放0.9倍，并逆时针旋转6°后，粘贴于图像中，得到 A1区域，如图 2（c）所示。其他区域的篡改方法类似，不再赘述。

4.2 评测标准

使用像素检测准确率（Pixels Detection Accuracy, PDA）和像素虚警率（Pixel False Positive,PFP）对算法进行量化评估[19]。其中，PDA 指被复制粘贴的像素实际被检测到的概率，PFP指检测为复制粘贴区域而实际上不是复制粘贴区域的像素个数占检测为复制粘贴区域的像素个数的比值。

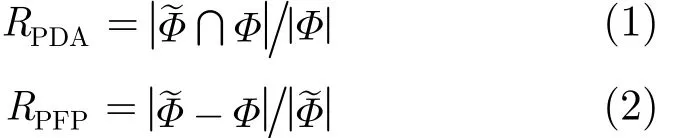
其中，PDAR 表示计算得到的像素检测准确率，PFPR表示计算得到的像素虚警率。Φ为复制粘贴区域的实际像素，~Φ为被检测为复制粘贴区域的像素。x为x中的像素个数。

期望、熵和超熵是代表云模型的三大数字特征。期望作为整个云图的中心值，是隶属度最大、最能表达定性要求的点；熵值则表达出了云的模糊性，指的是云模型在整个坐标区域的跨度大小；超熵代表了不确定性，超熵越大，云模型的离散程度越大，云图越分散。

另外，使用复制粘贴区域块数检测成功率（Block Detection Rate, BDR）表示算法检测出来的复制粘贴区域的块数占被篡改图像复制粘贴区域总块数的比率：

图2 测试图像示例

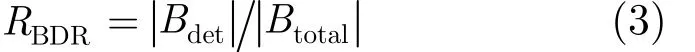
其中，Bdet表示检测出来的复制粘贴区域的块数，Btotal表示复制粘贴区域的实际总块数。 RBDR表示计算得到的复制粘贴区域块数检测成功率。

4.3 性能分析

Rg2NN算法中的各个参数对算法的检测性能有不同的影响，调整各参数，找出最佳阈值。

以0.05为步长，在0.1到0.9范围内对 TRg2NN进行调整，画出真阳性率（True Positive Rate, TPR）和假阳性率（False Positive Rate, FPR）的受试者工作特征（Receiver-Operator Characteristics, ROC）曲线，如图3（a）所示。其中，TPR表示篡改图像被成功识别的比率，FPR表示原始图像被识别为篡改图像的比率（在图像中计算出4对具有相同仿射变换关系的匹配特征点时，即把该图像判断为篡改图像）。在 TRg2NN为0.5时，取得最佳值，此时TPR=0.9873, FPR=0.051。Npix设为0或5时，虽然PDA较高，但距离过近的特征点因为相似的纹理特征被误判为匹配特征点，所以 PFP非常高。pixN 设为10到40之间的值时，均可得到理想的结果，本文实验中设为20。把BWT 以0.05为步长，从0.1到0.9进行调整，PDA和PFP的ROC曲线如图3（b）所示。BWT 设为0.7时取得最佳结果。当smallA 为0.01%和 0.02%时，均不会把较小的复制粘贴区域误当作噪声，而且smallA 为0.02%时滤除噪声的效果更好。当smallA 大于0.02%时，虽然可以滤除更多的噪声，但也会误删除较小的复制粘贴区域，导致 PDA降低，如图 3（c）所示。

4.4 算法比较

能够对多重复制粘贴篡改进行检测的算法除Rg2NN和g2NN外，还有文献[19]的算法。文献[19]提出，对图像循环使用检测算法，每次检测出一对复制粘贴区域，在下次检测时，掩盖上次计算出来的复制粘贴区域，不再提取其中的特征点。把每次循环的计算结果合并在一起，得到最终多重复制粘贴篡改检测结果。把这种方法和SURF特征提取算法、2NN特征匹配算法相结合，以便能够和本文算法比较。

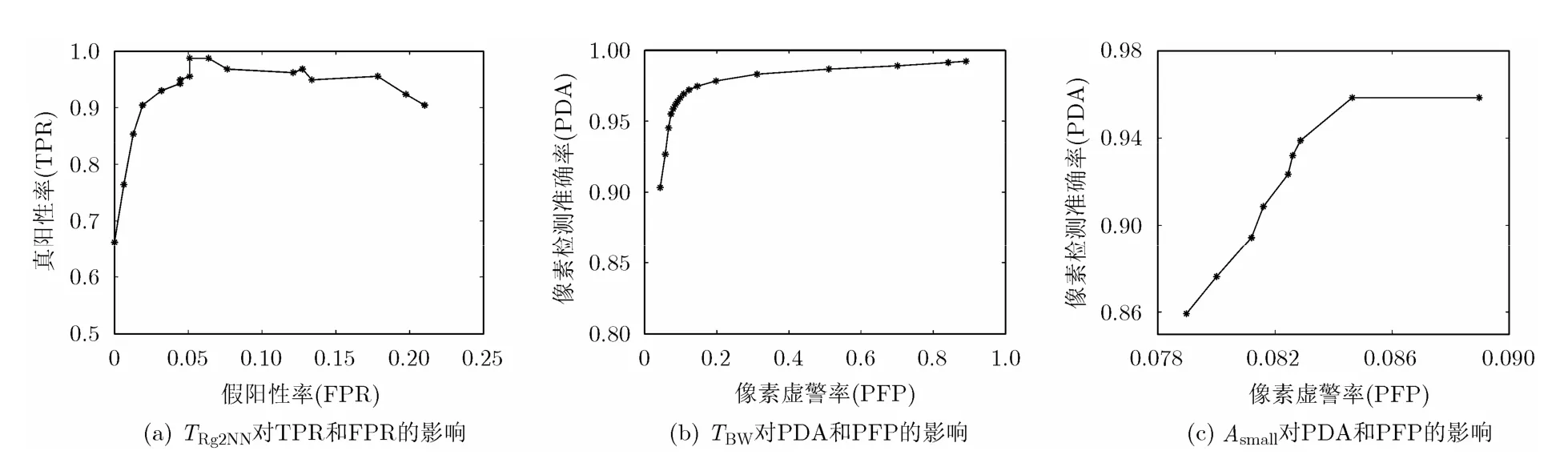
图3 算法参数对检测性能的影响

文献[19]的缺陷是当复制粘贴区域块数为奇数时，不能得到准确的检测结果。g2NN算法计算匹配特征点时不够准确全面，因此在计算复制粘贴区域轮廓时会漏检某些区域或不够精确。分别使用g2NN算法、文献[19]算法和Rg2NN算法对图2中的篡改图像进行检测，计算结果如图4所示。

4.5 鲁棒性测试

图像被篡改后，通常会被加入高斯白噪声或使用JPEG算法进行有损压缩，以降低图像质量，增加图像取证的难度。对测试图库集中的所有被篡改图像使用JPEG算法进行压缩，压缩后的图像质量分别为100, 90, 80, 70和60。分别使用2NN算法、g2NN算法、文献[19]算法和Rg2NN算法对压缩后的图像进行检测，BDR, PDA和 PFP分别如图5（a）～5（c）所示。对图像加入不同程度的高斯白噪声后，图像的峰值信噪比（Peak Signal to Noise Ratio,PSNR）分别为50, 45, 40, 35和30。分别使用2NN算法、g2NN算法、文献[19]算法和本文提出的Rg2NN算法对加入高斯白噪声的图像进行检测，BDR, PDA 和 PFP 分别如图 6（a）～6（c）所示。

4.6 计算时间

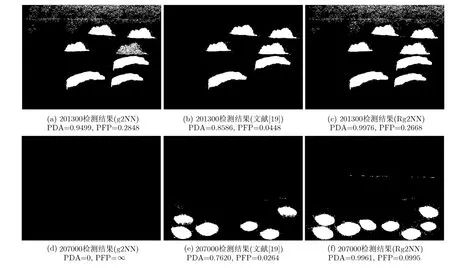
图4 多重复制粘贴篡改检测结果

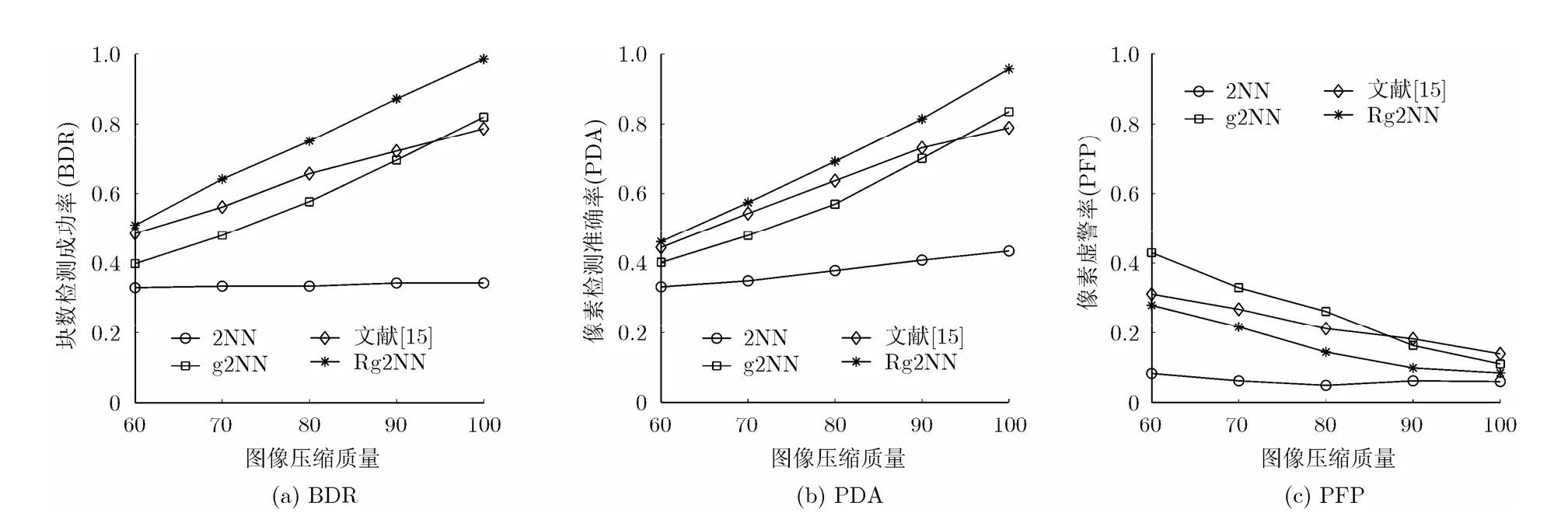
图5 JPEG有损压缩对算法的影响

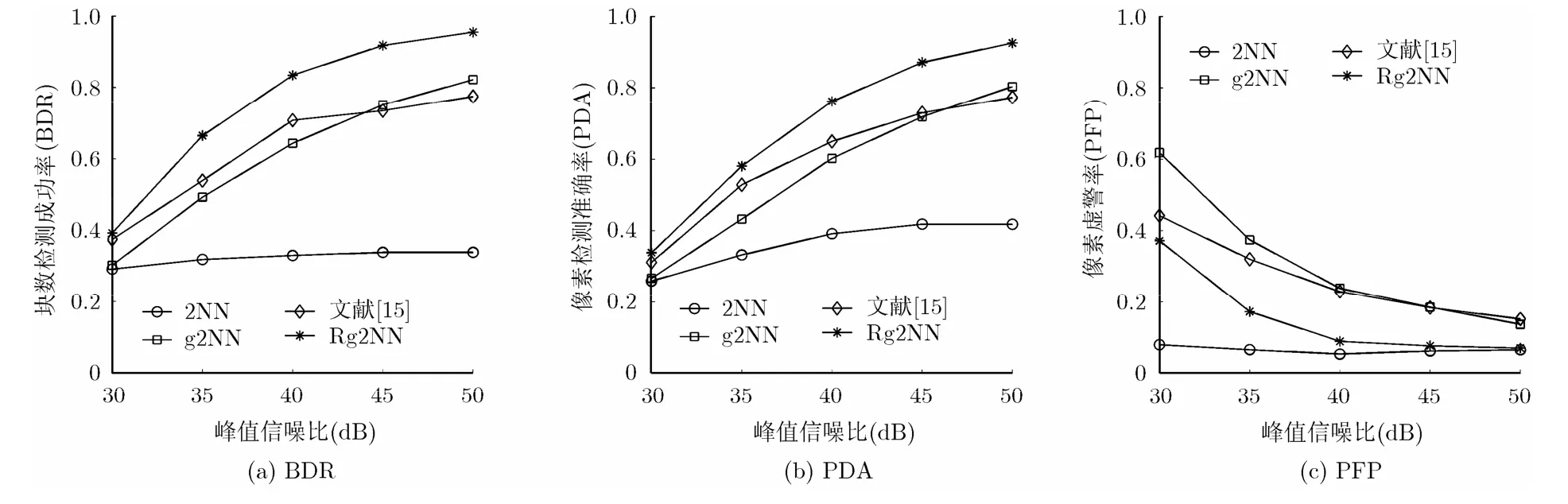
图6 高斯白噪声对算法的影响

由于 Rg2NN算法采用逆序方式计算匹配特征点，需要比g2NN算法计算更多相邻距离的比值，因此Rg2NN算法比g2NN算法的计算时间更长。另外，由于 Rg2NN算法计算得到的匹配特征点更多更加准确，因此在对特征点进行区域划分和对多重复制粘贴区域进行定位时也需要更多的计算时间。2NN算法只比较最近距离和次近距离的比值，因此计算时间少于g2NN算法。文献[19]算法需要反复对图像进行特征提取，计算匹配特征点，因此也比较耗时。使用本文的测试图库集进行实验，Rg2NN算法的平均计算时间为44.00 s, 2NN算法为20.48 s, g2NN 算法为 24.79 s，文献[19]算法为 53.37 s。

5 结束语

本文提出一种数字图像多重复制粘贴篡改检测算法，首先提取待检测图像中的SURF特征点，然后使用 BBF算法对每个特征点计算近邻，并使用Rg2NN算法计算匹配特征点，根据特征点之间的仿射变换关系划分特征点区域，最后对多重复制粘贴区域进行定位。该算法采用逆序方式计算特征点匹配对，避免了g2NN算法中匹配特征点的漏检情况，当待检测图像中有多重复制粘贴篡改发生时，可以更加准确的计算出特征点之间的仿射变换关系，并准确计算出每块复制粘贴区域。

[1] Qazi T, Hayat K, Khan S U, et al.. Survey on blind image forgery detection[J]. IET Image Processing, 2013, 7（7）:660-670.

[2] Al-Qershi O M and Khoo B E. Passive detection of copymove forgery in digital images: state-of-the-art[J]. Forensic Science International, 2013, 231（1/3）: 284-295.

[3] Ali Qureshi M and Deriche M. A review on copy move image forgery detection techniques[C]. Proceedings of the 11th International Multi-Conference on Systems, Signals &Devices （SSD）, Barcelona, Spain, 2014: 1-5.

[4] 王青, 张荣. 基于DCT系数双量化映射关系的图像盲取证算法[J]. 电子与信息学报, 2014, 36（9）: 2068-2074.Wang Qing and Zhang Rong. Exposing digital image forgeries based on double quantization mapping relation of DCT coefficient[J]. Journal of Electronics & Information Technology, 2014, 36（9）: 2068-2074.

[5] Wu Y, Deng Y, Duan H, et al.. Dual tree complex wavelet transform approach to copy-rotate-move forgery detection[J].SCIENCE CHINA Information Sciences, 2014, 57（1）: 1-12.

[6] Wang W, Dong J, and Tan T N. Exploring DCT coefficient quantization effects for local tampering detection[J]. IEEE Transactions on Information Forensics and Security, 2014,9（10）: 1653-1666.

[7] Niu S Z, Meng X Z, and Cui H L. Digital image forensics using orthogonal 1-D objects[J]. Chinese Journal of Electronics, 2014, 23（3）: 545-549.

[8] Liu B, Pun C M, and Yuan X C. Digital image forgery detection using JPEG features and local noise discrepancies[J]. The Scientific World Journal, 2014（1）: 1-12.

[9] Fridrich A J, Soukal B D, and Lukáš A J. Detection of copy-move forgery in digital images[C]. Proceedings of the Digital Forensic Research Workshop, Cleveland, USA, 2003:55-61.

[10] Popescu A C and Farid H. Exposing digital forgeries by detecting duplicated image regions[R]. Department of Computer Science, Dartmouth College, 2004.

[11] Jaberi M, Bebis G, Hussain M, et al.. Accurate and robust localization of duplicated region in copy-move image forgery[J]. Machine Vision and Applications, 2014, 25（2）: 451-475.

[12] Bo X, Junwen W, Guangjie L, et al.. Image copy-move forgery detection based on SURF[C]. Proceedings of the International Conference on Multimedia Information Networking and Security （MINES）, Nanjing, China, 2010:889-892.

[13] Mishra P, Mishra N, Sharma S, et al.. Region duplication forgery detection technique based on SURF and HAC[J]. The Scientific World Journal, 2013（1）: 1-8.

[14] Chen L, Lu W, Ni J, et al.. Region duplication detection based on Harris corner points and step sector statistics[J].Journal of Visual Communication and Image Representation,2013, 24（3）: 244-254.

[15] Amerini I, Ballan L, Caldelli R, et al.. A SIFT-based forensic method for copy-move attack detection and transformation recovery[J]. IEEE Transactions on Information Forensics and Security, 2011, 6（3）: 1099-1110.

[16] Bay H, Ess A, Tuytelaars T, et al.. Speeded-up robust features （SURF）[J]. Computer Vision and Image Understanding, 2008, 110（3）: 346-359.

[17] Beis J S and Lowe D G. Shape indexing using approximate nearest-neighbour search in high-dimensional spaces[C].Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, Puerto Rico, 1997: 1000-1006.

[18] Amerini I, Ballan L, Caldelli R, et al.. Copy-move forgery detection and localization by means of robust clustering with J-linkage[J]. Signal Processing: Image Communication, 2013,28（6）: 659-669.

[19] Kakar P and Sudha N. Exposing postprocessed copy-paste forgeries through transform-invariant features[J]. IEEE Transactions on Information Forensics and Security, 2012,7（3）: 1018-1028.

[20] Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004,60（2）: 91-110.

[21] Toldo R and Fusiello A. Robust multiple structures estimation with J-linkage[C]. Proceedings of the 10th European Conference on Computer Vision, Marseille, France,2008, 5302: 537-547.

[22] Suzuki S. Topological structural analysis of digitized binary images by border following[J]. Computer Vision, Graphics,and Image Processing, 1985, 30（1）: 32-46.

[23] Jegou H, Douze M, and Schmid C. Hamming embedding and weak geometric consistency for large scale image search[C].Proceedings of the 10th European Conference on Computer Vision, Marseille, France, 2008, 5302: 304-317.