基于可重构测量模型的网络测量任务部署算法

王 晶 汪斌强 张校辉

1 引言

随着网络技术的飞速发展以及网络应用的空前膨胀，网络规模、网络链路速率以及各种新兴网络应用都对网络测量提出了新需求和新挑战[1]。网络测量不仅需要满足更加多样化的测量需求，提供更加准确、实时的测量结果，还需要支持并发测量任务的动态加载。网络测量资源与多测量需求之间的矛盾日趋凸显。

针对测量资源与测量需求之间的矛盾，现有主流的研究方法可分为两类。一类从测量体系结构着手，设计新型测量模型和算法，从根本上提高网络测量技术的灵活性和可扩展性。此类研究的代表成果包括美国加利福尼亚大学Yuan等人[2]提出的可编程测量，文献[3, 4]提出的软件定义网络测量（Software Defined Measurement, SDM）、东南大学研制的虚拟化网络测量平台[5]以及中科院的研究团队提出的云服务网络测量与分析架构[6]等。另外一类研究更加关注测量任务部署、网络测量资源分配与测量准确性之间的关系[712]-，从测量任务和资源部署及调度算法着手解决上述问题，认为提高网络测量资源的利用率是解决该问题的根本途径。其中Qin等人[12]提出了一种基于无向图着色的测量任务调度算法 GCTS，分析由于测量资源争用而导致的任务冲突问题，并给出解决方案。美国南加州大学的研究团队在文献[3, 4]中分析讨论了在SDM中测量资源与测量准确性之间的关系，明确指出测量资源的分配和调度是 SDM 的重要研究内容，并且针对测量任务之间的 TCAM 资源分配问题给出一种启发式的算法。

为了解决在有限测量资源上承载多样化测量任务的问题，可重构的网络测量模型NMRM[13]（Network Measurement Reconfiguration Model）通过分层方法，将测量资源与测量需求分离，实现灵活、可扩展的网络测量功能。NMRM中的适配层依据测量任务和网络测量资源状况，为测量需求计算出最合适的任务部署方案。如何调度网络测量资源，为测量任务分配合理的测量构件，在不同任务之间复用测量构件，会直接影响 NMRM 中的资源利用率以及对于多样化并行测量任务支持的能力，因此测量任务部署问题是NMRM中的重要研究内容。

本文基于NMRM提出一种测量任务部署算法。首先对可重构测量模型中的任务部署问题进行抽象描述，并将问题转换为网络节点映射问题；然后给出问题的优化求解方法；最后通过实验仿真对算法进行分析验证。实验结果表明在任务部署成功率和任务平均等待时间这两个性能上，本文算法都比传统的GCTS算法有更好的表现，并且当任务冲突率和任务规模数量增加时，算法的部署成功率都能保证在90%以上。

本文第2节对可重构网络测量中的测量任务部署问题进行数学建模及转换；第3节给出详细的任务部署算法；第4节进行算法性能分析与仿真实验；第5节进行总结。

2 问题描述

2.1 测量任务部署模型

基于可重构测量模型的网络测量任务部署模型包括测量网络、测量构件和测量任务这3个重要元素，首先对它们进行描述。

（1）测量网络 测量网络是指由包含测量资源的测量节点及节点间的链路组成的底层物理网络，用无向图 GM=（NM, EM）表示， NM是测量节点集合， EM是边链路集合。在可重构的测量网络中，测量网络等价于实际的网络。NM中第i个网络节点ni上已配置的测量构件用集合 Ci表示，总计算资源和总存储资源分别用和示；节点u, v间的边链路 eu,v上的总传输带宽资源用表示。

（2）测量构件 测量构件是组合构成测量算法的基本单元[13]，通过构件间的组合，能够动态灵活地实现各种测量功能，从而支持各类测量任务。测量构件消耗的资源可用资源消耗函数来刻画，本文中仅考虑测量构件的计算资源、存储资源和带宽资源消耗。计算资源消耗函数cj）和存储资源消耗函数（i, cj），分别用于计算测量网络节点 ni中测量构件 cj所消耗的计算资源和存储资源。带宽资源消耗函数（i, ck, j, cl）用于计算节点 ni中测量构件 ck和节点 nj中测量构件 cl通信所消耗的链路带宽资源。不同构件的资源消耗函数不尽相同。节点剩余的计算资源、存储资源分别用和表示，节点间链路剩余的带宽资源用表示，计算公式分别

其中k表示节点 ni上配置的测量构件总数，costc）为节点上用于其它功能的计算资源开销，costm（）为节点上用于其它功能的存储资源开销；n, m分别表示节点 nu和 nv上配置的测量构件总数量， c ostb（e ）为链路上的其它带宽资源开销。

u, v（3）测量任务测量任务是对测量对象、测量内容等要求的综合描述。测量对象拓扑 GT是测量网络GM的子图，用 GT=（NT, ET） 表示，且 NT⊆NM,ET⊆EM。测量内容包括网络流量特征、带宽、传输时延、拓扑结构等。依据测量内容和测量拓扑，结合测量工具和方法可直接计算得到测量任务的优选测量构件配置集合 CT。 CT是在不考虑网络整体测量资源分布情况下，为完成测量任务，在网络测量节点上所需配置的测量构件集合的最优方案。CT中测量构件所部署节点以及构件间通信的链路构成测量构件优选配置网络，由无向加权图GP=（NP, EP）表示，对于 ∀ n '∈ NP，满足 n '∈NM,∈ EP，满足∈EM。优选配置网络和优选测量构件配置集合构成测量任务的优选部署方案。而在实际测量任务部署时，由于任务间存在资源竞争和冲突，因此测量优选部署方案并不一定是全网最优的部署方案。

对于一个测量任务，在 NMRM 模型中可能存在多个等价部署方案。因此 NMRM 模型中的测量任务部署问题可以描述为依据全网资源及任务状态在多个等价部署方案中选择最佳方案的问题。基于以上分析和描述，测量任务的部署问题可以抽象为测量任务优选配置网络 GP到底层测量网络 GM的满足测量构件资源消耗约束等要求的映射问题, CT是底层测量网络为测量任务分配的测量构件集合，M:GP↦ （GM, CT） 。

测量任务优选配置网络到底层测量网络的映射可以分解为节点映射和链路映射。节点映射是指在底层网络中为 GP的节点选择合适的部署位置。为提高映射效率，只在等价测量节点中为 GP中的节点寻找映射点。等价测量节点是指能够完成与已知优选部署节点相同测量功能、满足相同测量性能的测量节点，用EQ）表示优选网络节点的等价节点集合。节点的映射过程可形式化描述为 Mn:NP↦EQ（NP）。在可重构的网络测量模型中，等价节点与优选网络节点上的测量构件配置并不一定相同，不同的构件配置通过组合关系后可达到等效的测量能力。但由于网络测量结果的准确性和实时性会受到测量点物理位置的影响，因此等价节点间的网络距离会受到测量任务的制约。EQ）中的节点满其中，dis（ni）是节点距离的跳数， DT是由测量任务T确定的等价节点半径，描述了节点与其等价节点之间的最远距离。图1为测量节点的映射示意图。假设图1中，对于节点A存在两个等价节点E和F，可以通过在E和F上配置不同的测量构件完成相同的测量任务。

链路映射是指在底层网络中为 GP中的链路选择部署路径Path= l1,l2,…,lk, li是部署路径上的一条链路。测量链路的映射依赖于通信测量构件部署节点之间的路径连接情况，用 P H）表示在节点和之间可用于任务 T的测量链路部署路径集合。图2是测量路径与部署路径集合之间的映射关系示意图。GP中的链路用于部署主动测量任务时测量构件间通信。在进行链路映射时，应确保链路部署路径上瓶颈链路的剩余带宽与用于任务T的测量构件间通信所消耗的传输带宽率比值大于α，即 P H）中的路径满足：。其中，公式中的分母部分是节点 nu和 nv之间用于任务 T的测量构件间通信所消耗的传输带宽资源， Rb是

图1 测量节点映过程射示意图

图2 测量路径映射示意图

u, v

该部署路径上的瓶颈链路的剩余传输资源，α是预先设定的一个阈值，它代表主动测量任务对于链路带宽剩余比例的要求水平。链路的映射过程可形式化描述为： Me: EP↦ P H（EP）。

2.2 测量任务部署原则

基于合理利用网络有限资源，降低测量任务部署成本，使底层网络能够尽可能多地承载测量任务，提高测量任务部署成功率，本文提出3条测量任务部署原则。

（1）测量资源均衡利用原则：在部署测量任务时，要尽量将测量任务均匀地部署到网络节点上。

（2）部署代价最小化原则：通过将具有相同测量构件需求的测量任务映射到相同底层节点的方法，利用测量构件复用的特点，降低测量构件组合开销；在进行链路映射时应尽可能减小测量节点构件间通信路径的长度，以降低构件通信开销。

（3）链路优先映射原则：在进行测量任务部署时，若存在链路映射，则优先考虑按优选部署网络中的方案进行链路映射。

3 基于可重构测量模型的测量任务部署算法

3.1 评价指标

测量任务部署问题由节点映射和链路映射两部分问题构成，因此分别对节点和路径进行评价。

首先定义节点的测量任务适合度γ（n',n），描述底层测量节点n对于测量任务优选部署节点n'的适合度。式（7）是节点测量任务适合度的计算公式，其中K是测量任务在优选配置节点n'上部署的测量构件总数； xk∈ { 0,1}，当 ck∈Cn,xk= 1 ，否则xk=0; λ1, λ2为权重因子，且λ1+λ2=1。在式（4）中，与λ1相乘的部分描述了n上的剩余计算资源和存储资源能力，与λ2相乘的部分表示在nM已配置的测量构件在 nP所需配置测量构件中占有的比例。σ是一个极小正数，用于避免当n中没有配置优选测量构件时，λ2的加权部分为0。φ（n',n）是节点作为链路映射的一个端点时，它对于优选部署节点的适宜度。当优选部署节点n'的连接度大于0且n' = n时，即n'就是n，且是链路映射的一个端点，那么φ（n',n）=D（ n'）；否则若节点n'的连接度等于0，即n'不是链路映射的端点时，φ（n',n）=0。D（ n'）是节点n'的连接度。其中和的计算公式为式（1），式（2）。

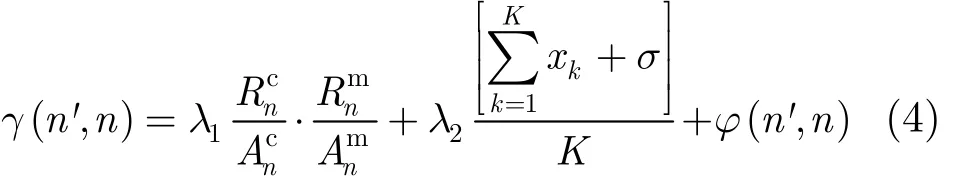
通过式（4）计算得到的γ，不仅考虑了节点资源的处理能力和节点上测量构件的类型，同时还考虑了当存在构件通信时应尽可能将优选节点映射到其节点本身。λ1和λ2的比值体现了在对节点的评价时，剩余资源与构件类型的比重。γ的值越大，说明节点的评价越高，越适合作为n'的映射目标。

u,v i,j i,j

算θ的前一个连乘项表示部署路径是否与优选部署网络中的链路相同，后一个连乘项的物理意义是部署路径上每条链路的带宽资源空闲率的乘积。θ＞1时，表示部署路径与优选链路一致；θ＜1时，表示部署路径与优选链路不一致。因此，θ值越大的部署路径，越适合作为 pu,v的映射目标。

3.2 部署算法

测量任务部署算法划分为两个处理步骤：

步骤1 预处理过程。当测量任务T到达后，首先生成任务 T的优选配置网络 GP和优选测量构件配置集合 CT，依据任务计算得到 GP中每个节点的等价节点集合；

步骤2 GP网络映射过程。首先将 GP中的节点分为连接度为0的节点集合和连接度不为0的节点集合，然后先映射中的节点以及节点之间的链路，最后映射中的节点。

表1中的算法采用广度优选搜索的方法遍历进行描述，在实际的部署算法中可采用其他的遍历算法。任务部署时，由于节点和链路的映射存在先后顺序，可能会出现由于节点或链路的资源不能满足映射要求的情况，从而导致映射失败。为此，算法在选择最优映射节点和链路时（算法的第 6, 13, 19,28步），还同时记录一个次优的映射目标作为备选项，当在最优目标上映射失败时，立刻选择次优目标进行重新映射，从而提高测量任务部署的成功率。

3.3 算法性能理论分析

首先对MTDANMRM算法的最坏时间复杂度进行分析。由于算法中的1, 2两步不涉及映射过程，这部分的时间开销可假设为一个常量κ，转换得到的 GP中的节点数量为n。算法的最坏执行情况为优选部署网络 GP是一个全连通图，在这种情况下算法每次在对一个节点进行映射后映射完一个节点，需要为其相邻的所有边进行映射。映射每条边的时间是寻找K条最短路径的时间，该值与底层网络 GM规模相关，在分析算法间复杂度时可假设底层网络规模固定，该部分开销用常数η表示。那么，MTDANMRM 算法的最坏时间复杂度的计算公式就为

MTDANMRM 算法将测量任务部署问题转换为优选部署网络 GP到底层基础网络 GM的映射问题，虽然算法的时间复杂度为 O （ n2），但由于MTDANMRM通过测量等价测量节点替换以及测量构件配置加载等的方法，替代非重构模型下测量任务部署过程中测量任务延时等待的方法，使得测量任务在实际部署过程中的等待时间反而有所降低，具体仿真结果见4.2节。

表1 基于测量重构模型的测量任务部署算法

MTDANMRM 算法的收敛性表现为通过运算可得到在有限测量资源上部署多样化的测量任务的优化方案，可用测量任务部署成功率对算法的收敛性进行描述。用4.1节中描述的仿真环境进行实验，仿真测量任务的部署成功率。设置任务数量为1000，任务冲突概率为0.5，共进行1000次独立实验，统计任务部署成功率95%≥的情况，结果如表2。仿真结果表明，在1000次实验中部署成功率超过95%的次数占总实验次数的 98.3%，由此证明MTDANMRM算法具有较好的收敛性。

表2 算法部署成功率仿真结果

4 算法性能仿真与分析

4.1 模拟仿真环境及方法

仿真实验在Pentium 4 CPU 2.8 GHz, 1.0 G内存的处理器上进行，测量任务的设置参考文献[12]中的方法，底层测量网络拓扑由 GT-ITM[14]生成，包含200个节点和1083条链路。实验假设测量任务的存活时间在[11,100]单位时间上服从均匀分布，任务执行时间在[2,10]上服从均匀分布，测量任务到达事件服从均值为5的泊松分布。底层网络包含200个节点和1125条链路，节点上的存储资源和计算资源分别在[1,100]和[1,10]的区间上服从均匀分布，链路带宽在[50,100]之间服从均匀分布。仿真实验共支持10种测量构件组合，每种测量构件所需要的资源计算函数为确定函数。另外，假设每个测量构件的配置和组合时间不超过测量任务执行时间的1/β。每组仿真分别独立进行100次实验，仿真结果为实验平均值。

假设每个测量任务将随机转换为一个优选配置网络 GP, GP中的节点数服从[3, 8]区间上的均匀分布，节点位置按任务之间的冲突概率[14]随机确定，每个节点所需要配置的测量构件数量在[1,5]区间上服从均匀分布，构件类型在10种构件间随机产生，依据其产生的构件类型确定节点之间的链路。

4.2 仿真实验结果分析

图3 不同遍历方法下测量任务部署成功率

分别用广度优先搜索和深度优先搜索方法对算法进行仿真，通过实验结果来分析不同遍历方法对于MTDANMRM性能的影响，设定参数 λ1= 0 .5,λ2= 0 .5。我们观察了在不同任务冲突概率下测量任务的部署成功率，在100个测量任务和500个测量任务的情况下分别进行仿真实验。图3为不同遍历方法下算法的部署成功率。图中的两条曲线基本吻合，说明图的遍历算法对于MTDANMRM算法性能的影响不大。后续的仿真实验均选用广度优先搜索方法。λ1, λ2是算法中两个重要的参数，直接影响算法对于等价节点的选择。通过仿真实验，观察参数λ1,λ2对算法性能的影响。实验分别仿真了不同λ取值情况下，测量任务部署成功率、测量任务平均等待时间、测量节点资源利用均衡性这3个性能指标，其中节点资源利用均衡性用节点资源利用率的均方差来刻画。实验设定任务冲突概率为0.5，任务数量为100，图4是实验仿真的结果。结果表明，λ值的变化对于算法的任务部署成功率影响不大，但其对于任务平均等待时间和测量节点资源利用率均方差这两个指标的影响较大。随着2λ取值的增加，任务的平均等待时间减小，而测量节点的资源利用率均方差增大。这是由于1λ的值越大，算法在进行节点映射时越趋向于选择资源剩余多的节点，这样会导致节点资源利用率越趋于均衡；而2λ的值越大，算法越趋向于选择具有同类型测量构件的节点，这样在进行测量任务部署时会减少新测量构件配置和组合的时间。

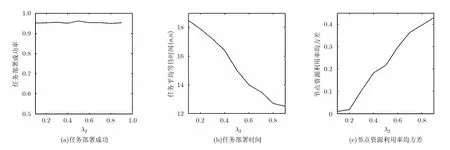
图4不同λ取值下算法性能仿真

图5 是在任务数量为100时，不同任务冲突概率情况下算法性能仿真结果。图 5（a）中的数据说明在任务部署成功率方面， MTDANMRM算法明显高于 GCTS，并且随着任务冲突概率的增加，两个算法之间的差异越大，即在任务冲突概率较大的情况下，本文的MTDANMRM算法具更高的部署成功率。从仿真数据上看，任务部署成率不低于90%。这是由于MTDANMRM算法基于可重构的网络测量模型，当测量任务发生冲突时，若任务所需的测量构件相同，可通过复用构件的方式提高任务部署成功率。图 5（b）是任务平均等待时间的仿真结果，图中下方的3条曲线分别为MTDANMRM算法在不同的β取值下的仿真结果。实验结果证明，MTDANMRM 算法的任务平均等待时间远小于GCTS算法，任务冲突概率对于任务平均等待时间的影响不明显，这是由于两种算法导致任务等待时间不同的原因，MTDANMRM算法中导致任务等待的时间主要来源于测量构件的配置和组合，若测量构件不需要重新配置，那么将不会引入等待时间。此外，β会对 MTDANMRM算法的任务等待时间造成影响，β值越小，那么测量构件的配置和组合时间将越长，导致任务平均等待时间越长。

图5 不同任务冲突概率下的仿真结果

图6 不同任务数量规模下的仿真结果

图6 是当任务冲突概率为0.5时，不同任务数量下算法性能仿真结果。图6（a）中的实验结果说明，随着测量任务数量的增加，GCTS的任务部署成功率会明显下降，而MTDANMRM算法的任务部署成功率受任务数量的影响较小，在任务数量为1000时，其部署成功率仍可达92.21%。在任务平均等待时间上，两种算法的仿真结果均会随着部署任务数量的增加而增加，但MTDANMRM较GCTS的平均等待时间有显著下降，并且随着β值的增加，任务平均等待时间会有所降低。

4.3 真实环境实验分析

在模拟仿真基础上，为进一步验证算法性能，采用NetFPGA 搭建了包含6个网络交换节点和1个控制节点的网络流量测量实验系统，图7是网络拓扑结构。图7中的N1～N6节点是6个用NetFPGA实现的底层交换节点，每个交换节点上通过编程可实现均匀抽样、关键字匹配、hash映射、计数器4种测量构件，C是控制节点 ，通过运行MTDANMRM算法对测量任务进行优化部署，并通过openflow协议接口对6个交换节点上的构件进行配置。每个交换节点上的TCAM, SRAM等资源以及每种测量构件的资源占用情况均通过编程进行设置，交换节点之间的流量通过测试仪注入。

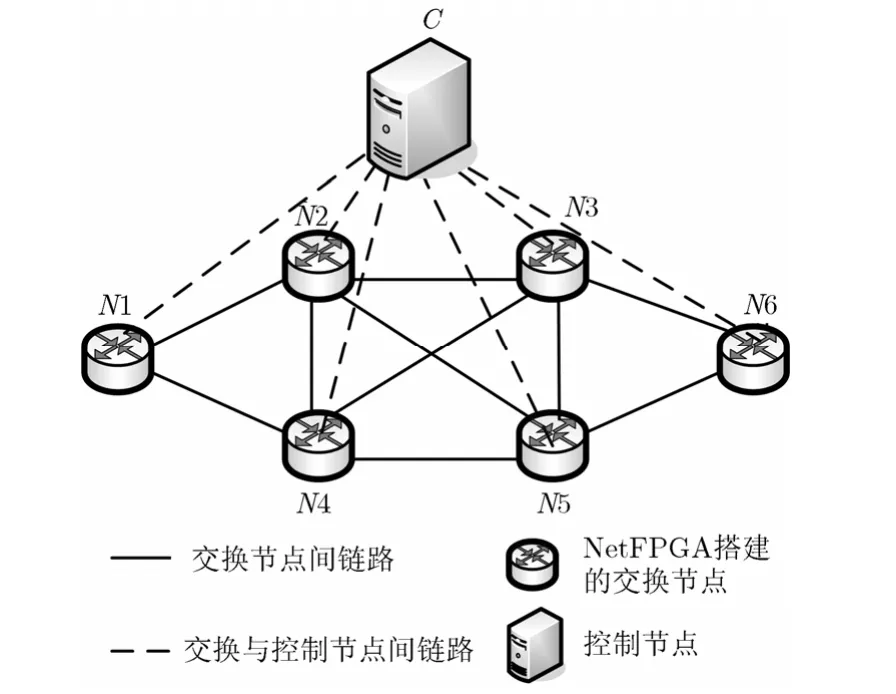
图7 不同任务数量规模下仿真结果

在实验网络中部署 10个独立的测量任务来测试算法在资源利用均衡性、任务部署成功率方面的性能。用于测试的测量任务属于最大流识别、可用带宽测量以及流量分布统计这3个类型，每种测量任务需要通过在节点上部署不同的测量构件来完成，表3是具体的测量任务。MTDANMRM算法中的参数设置为 λ1= 0 .5, λ2= 0 .5。实验结果显示，通过MTDANMRM算法，任务部署成功率达100%，网络节点资源利用率均方差为0.153。此外，对任务1,4,7,10的测量结果进行统计分析，它们对最大流的识别率均超过 98.2%。真实环境的实验结果与仿真数据实验结果一致说明，MTDANMRM算法在进行多样化测量任务部署时，能够有效提高任务部署成功率，改善测量资源利用不均衡的问题。

5 结束语

本文针对有限测量资源与多样化测量需求之间的矛盾日趋激化的问题，基于可重构的网络测量模型，设计了一种网络测量任务部署算法MTDANMRM。该算法将测量任务转换为测量优选配置网络，利用测量构件的组合复用原理，通过网络映射算法对问题进行求解，实现了全网范围内的测量任务优化部署，从而达到高效利用网络测量资源和支持测量任务动态并发部署的目的。

MTDANMRM 算法对于部署失败的任务没有给出合理的调度策略。如何将现有任务进行合理的迁移，对网络测量资源进行重新整合，是有待进一步研究的问题。此外网络测量任务到达特征、测量构件组合方法、测量构件资源消耗函数等都是后续研究的重点。

表3 测量任务内容

[1] 周爱平, 程光, 郭晓军, 高速网络流量测量方法[J]. 软件学报，2014, 25（1）: 135-153.Zhou A P, Cheng G, and Guo X J. High-Speed network traffic measurement method[J]. Journal of Software, 2014, 25（1）:135-153

[2] Yuan L, Chuah C N, and Mohapatra. ProgME: towards programmable network measurement[J]. IEEE/ACM Transactions on Networking, 2011, 19（1）: 115-128.

[3] Masoud M, Minlan Y, and Ramesh G. Resource/accuracy tradeoffs in Software-defined measurement[C]. HotSDN 2013- Proceedings of the 2013 ACM SIGCOMM Workshop on Hot Topics in Software Defined Networking, Hong Kong, China,2013: 73-78.

[4] Minlan Y, Jose L, and Rui M. Software defined traffic measurement with opensketch[C]. 10th USENIX Symposium on Networked Systems Design and Implementation, Lombard,IL, USA, 2013: 29-42.

[5] 曹争, 何建斌, 基于虚拟化的网络测量平台[J]. 通信学报,2013, 34（Sppl. 2）, 84-89.Cao Zheng, and He Jian-bin. Virtualization based network measurement platform[J]. Journal on Communications, 2013,34（Sppl. 2）: 84-89.

[6] 张潇丹, 李俊. 一种基于云服务模式的网络测量与分析架构[J]. 计算机应用研究, 2012, 29（2）: 725-729.Zhang Xiao-dan and Li Jun. Network measurement and analysis architecture of cloud service[J]. Application Research of Computer, 2012, 29（2）: 725-729.

[7] Masoud M and Minlan Y. DREAM: dynamic resource allocation for software-defined measurement[C]. Proceedings of the 2014 ACM Conference on Special Interest Group on Data Communication, Chigaco, IL, USA, 2014: 419-430.

[8] Yu C and Lumezanu C. FlowSense: monitoring network utilization with zero measurement cost[C]. Proceedings of Passive and Active Measurement 14th International Conference, Hong Kong, China, 2013: 31-41.

[9] Chowdhury S R and Bari M F. PayLess: a low cost network monitoring framework for software Defined Networks[C].2014 IEEE/IFIP Network Operations and Management Symposium, Krakow, Poland, 2014: 1-9.

[10] Tootoonchian A and Ghobadi M. OpenTM: traffic matrix estimator for openflow networks[C]. Proceedings of Passive and Active Measurement 11th International Conference,Zurich, Switzerland, 2010: 201-210.

[11] Yu Y and Qian C. Distributed collaborative monitoring in software defined networks[C]. Proceedings of the ACM SIGCOMM 2014 Workshop on Hot Topics in Software Defined Networking, Chigaco, IL, USA, 2014: 85-90.

[12] Qin Zhen, Cessa R R, and Ansari N. Task-execution scheduling schemes for network measurement and monitoring[J]. Computer Communications, 2010, 33（2）:124-135.

[13] Wan Jing, Wang B Q, and Zhu Ke. How to support the diversity of network measurement requirements[C]. The 2014 3rd of the International Conference On Sensor, Measurement And Intelligent Meterials, Zhuhai, China, Dec 5-7, 2014.

[14] Zegura E, Calvert K, and Bhattacharjee S. How to model an Internetwork[C]. Proceedings of the IEEE INFOCOM, San Francisco, CA, USA, 1996: 594-602.