分簇无线传感器网络中根校验全分集LDPC码设计与能效分析

郭 锐 刘春于 张 华 包建荣③ 姜 斌

1 引言

传感器节点能量有限，无线传感器网络差错控制技术需要在纠错性能和能耗之间折中。文献[1]首次以能效（energy efficiency）作为无线传感器网络差错控制技术能量消耗和可靠性之间折中的度量。近年来，文献[2,3]研究了基于LT喷泉码分布式不等错误保护（Un-equal Error Protecting, UEP）的差错控制方案；文献[4]对无线传感器网络中喷泉码的度分布进行了优化设计。文献[5]提出了在无线传感器网络中采用非二进制码字的纠错编码方案。文献[6]研究了Raptor码字的纠错编码方案。随着LDPC码编译码技术的发展，文献[7]研究了LDPC码在无线传感器网络中的纠错性能。文献[8]研究了采用ALOHA协议的无线传感器网络中，基于LDPC码的编码方案与码字速率设计。以上无线传感器网络纠错编码方案中，不论采用何种编码码字，都采用发端重传的 ARQ机制，但重传不仅会导致能耗的增加，而且在较差的信道环境中，收效甚微。

在无线传感器网络中，传感器节点采集的数据经不同的路由路径到达汇聚节点，其中蕴含着分集资源。根校验全分集LDPC码在块衰落信道下能取得分集增益[911]-；文献[12]通过设计特殊结构的LDPC码字在中继信道上实现不同的分集。文献[13]研究了无线传感器网络中通过空时编码，利用其协作分集的方式来提高编码性能的方法。因此，本文设计在无线传感器网络中能取得全分集的根校验LDPC码的结构，并给出编码方法与能耗。

2 分簇无线传感器网络结构

分簇无线传感器网络结构如图1所示，图中标出了A, B, C 3三个簇，节点被分成若干个簇，每簇由一个簇头节点和若干个簇成员节点组成。簇内的传感器节点将探测到的信息传递到簇头节点，簇头节点对收集到的本簇数据进行融合处理后传给汇聚节点（汇聚节点通常不受能量限制约束）。

图1 分簇无线传感器网络体系结构图

为了提高簇内通信的分集增益，降低因信道恶化或部分节点通信能力降低而导致整个传感器网络性能的下降，簇内传感器节点可以采用编码协作的方式与簇头进行通信。本文研究存在簇内编码协作情况下，根校验全分集LDPC码的构造与编码方案。首先，研究所采用的编码协作方案的固有分集；其次，设计速率兼容根校验全分集LDPC码并分析所提编码方案的能效。

3 无线传感器网络簇内编码协作通信

3.1 簇内编码协作通信方案

如图2所示，假设簇内两相邻节点S1, S2（称为伙伴节点）进行编码协作将数据传递给簇头节点D。簇内传感器节点以TDMA的方式与簇头进行通信，在第1帧，每个节点向伙伴节点和簇头节点广播自己的信息，在第2帧，S1或S2根据能否正确的译码出接收到伙伴节点的信息（第 1帧时采用 CRC校验），要么传输伙伴节点的信息，要么传输自己节点的信息。可以分为以下4种情况：

图2 簇内2节点编码协作通信示意图

假设第1帧、第2帧传输的码字长度分别为N1,N2，则在一个传输过程总码长 N = N1+ N2。协作水平为 b = N2/N。C11为节点S1第1帧传输的数据，C12为节点S1第2帧传输的数据，C21为节点S2第1帧传输的数据，C22为节点S2第2帧传输的数据（节点S1和节点S2在不同的时隙发送）。

簇头节点D需要知道当前传输采用以上哪种协作方式，这里采用节点S1，节点S2在传输中增加1 bit数据来指示当前状态。

3.2 编码协作方案的固有分集

编码码字的分集阶数等于系统固有分集数时称为全分集，假设接收端已知信道状态信息，信道增益服从平坦瑞利衰落，传感器节点i与簇头节点之间的瞬时信噪比记着 γi,d（n），则 gi,d（n）服从指数分布，其 均 值 记 为 Γi,d=E [ γi,d（n）]。 其 成 对 差 错 概 率（Pairwise Error Probability, PEP）表示为[14]

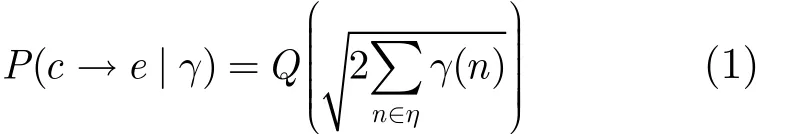
γ（ n）为接收端瞬时信噪比。c是传输的码字，e是译码后的码字。η 是所有 c（ n）≠ e（ n）n的集合。η=d是c和e之间的汉明距离。收发两端相互独立情况下，则条件成对差错概率可以表示为P（ d|γ）。

假设簇内每个传感器节点传输的两帧期间，信道的衰落保持不变，不同传感器节点传输期间，信道衰落不同，即 γi,d（ n ） = γi,d（n = 1,2,…,N ） ,i, j ∈{1,2}。因此，编码协作情况1下，节点S1的条件PEP可以表示为

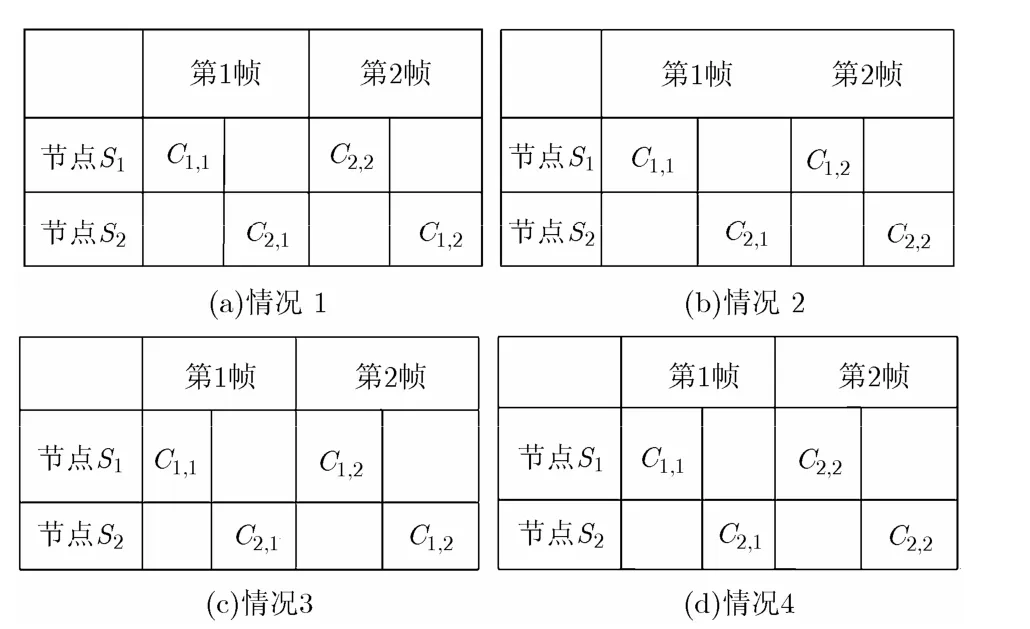
图3 两节点编码协作传输帧结构图

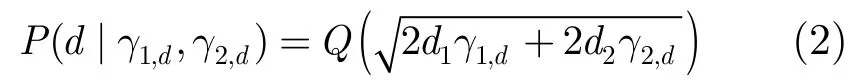
d1, d2分别为节点 S1，节点 S2发生错误的比特数。d1+ d2= d 。因此，有d位发生错误的PEP表示为

P（⋅）表示概率密度函数。利用Q函数的替代形式以及矩母函数（MGF），可得

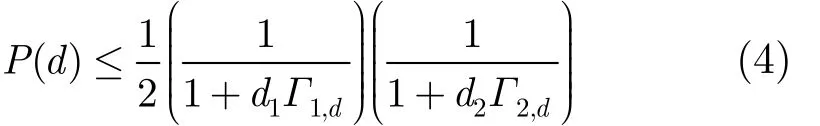
Γ1,d, Γ2,d分别为相应节点S1，节点S2发送时链路瞬时信噪比均值。当d1, d2非0，信噪比较大时，P（ d ）∝1/（Γ1,dΓ2,d） ，即分集阶数为2。

4 全分集LDPC码字的构造与实现

图4给出了在迭代译码算法下能取得分集阶数为2的全分集LDPC码的校验矩阵，称为根校验全分集LDPC码。图中I为单位矩阵，0为零矩阵。其中，1C , 2C为根校验节点，1C通过度数为1的根连接与信息比特1i相连，而与信息比特2i、奇偶校验比特2p则以任意度数连接，其度数由 H2i, H2p的列重决定；同样，2C通过度数为1的根连接与信息比特2i相连，而与在α1上传输的信息比特1i、奇偶校验比特1p则以任意度数连接，其度数由 H1i, H1p的列重决定，连线上的数字表示连接的度。假如传输过程中，2i发生了丢失或者不能译码成功，1i能够成功译码。采用根校验全分集LDPC码字能够通过译码恢复2i。

在无线传感器网络中采用所提协作编码方案，编码后的码字分为两帧，传感器节点 S1, S2与簇头节点需要实现对不同速率码字的编译码操作，因此需要设计速率兼容的全分集LDPC码，其校验矩阵构造如图5所示。

设计速率兼容LDPC码，主要有两种方法：打孔和扩展。扩展法设计速率兼容LDPC码通过增加校验比特来获得可变的速率。如图6所示，编码比特被分成3部分，信息比特i，两类校验比特1p,2p。第1帧，传输信息比特i、校验比特1p；第2帧，假设协作节点能正确译码接收到的信息，传输校验比特2p。

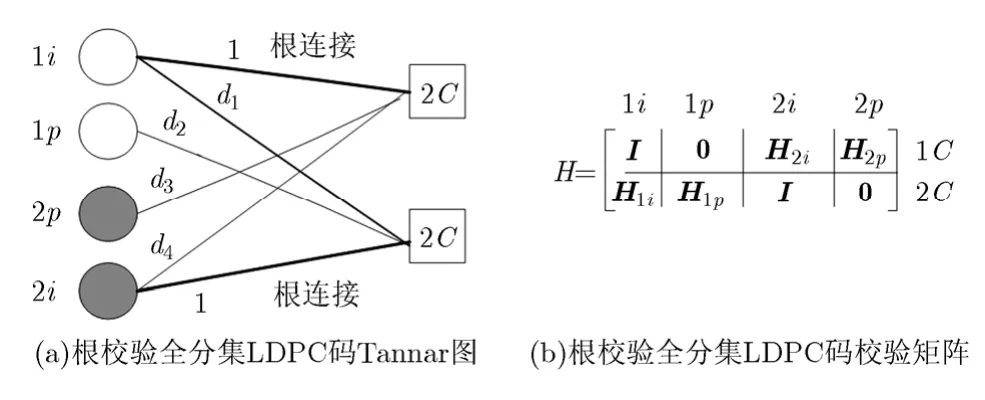
图4 根校验全分集LDPC码的Tanner图及其校验矩阵

将结构如图4的全分集LDPC码校验矩阵嵌入到图5所示结构的LDPC中，代替上述结构码字的H2部分，实现速率兼容全分集 LDPC码的设计。若要使2p和2i具有相同的编码增益，需要对称的码字结构。将图5码结构中的 H1以及0填充部分，用H1s和 H1r代替，得到如图6所示的速率兼容根校验全分集LDPC码。

图5 速率兼容LDPC码校验矩阵构造示意图

H1s保护1i, 1p, H1r保护2i,2p。为了方便起见， H1s,H1r可以具有同样的结构。假设 H1s的度分布多项式为 （λ1（ x ） ,ρ1（x）） ，根校验全分集 LDPC码的度分布多项式为 （λ2（ x ） ,ρ2（x）） ，则构造的速率兼容根校验全分集LDPC用多项式 （λ1（ x ） ,ρ1（ x ） ,λ2（x）,ρ2（x））来表示。H1s,H1r在满足度分布的情况下，可以随机生成，也可是具有QC结构的校验矩阵。为了方便对 H ,H 系统化，,设计成满秩矩1s1r阵。,是 H ,H 最右侧的方阵。H 具有全1s1r2分集LDPC码结构。

编码时，首先根据1sH ,1rH 确定校验位12,''p p，再根据2H决定（1,2）pp。然后将矩阵通过列变换实现系统化。译码时候，可以根据上述4种情况进行译码，比如在情况 1，汇聚节点将接受到的两帧组合起来，在包含1sH ,1rH 以及2H 的矩阵上进行译码。在情况4，只需要第1帧在1sH 上译码。

5 所提编码方案的能效分析

无线传感网络中，能量消耗包括发送和接收端所有电路模块的能耗和发射能耗[15]，如图7所示。

各参数的含义如下：PDAC,Pmix,PLAN,PIFA,Pfilt,PADC,Penc和 Pdec分别表示D/A转换器、混频器、低噪放大器、中频放大器、接收端滤波器、A/D转化器，LDPC编码器和LDPC译码器每处理1 bit的能耗，发射端电路能耗：

对于BPSK调制系统，在给定比特错误概率Pb时的PPA表示为[16]系统的发射能耗：

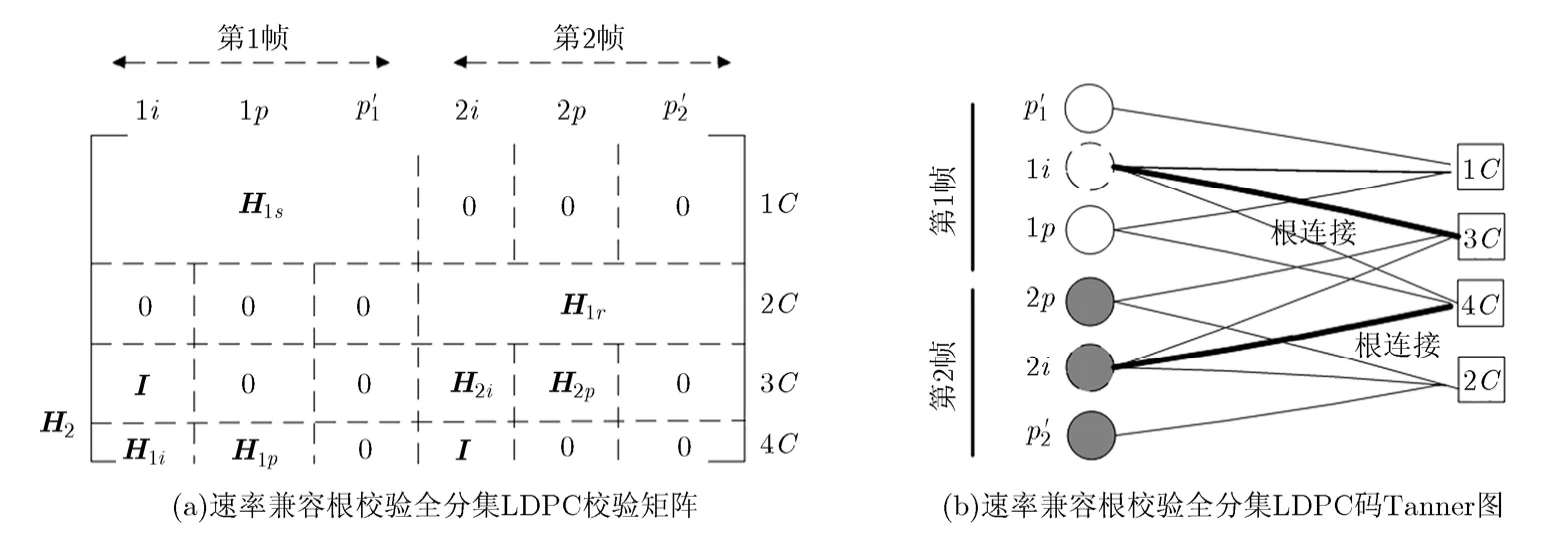
图6 速率兼容根校验全分集LDPC校验矩阵及Tanner图

式中 α =（ε/ κ）-1,ε调制星座的峰均比，κ 是RF功率放人器的泄露效率，Pb为平均误比特率，Rb为比特传输速率，N0为单边带噪声功率谱密度，Mt是硬件过程变化和其它加性背景噪声以及其它干扰的连接边缘补偿， Nf= Nr/N0为接收噪声模型， Nr为输入端总的噪声功率谱密度， Gt,Gr分别表示发射机和接收机的天线增益，为链路边缘补偿，d为传输距离，λ和发射频率有关。

接收端电路耗能：

总消耗能耗=接收端电路能耗RecP +发射端电路能耗transP +系统的发射能耗PAP 。以一含有M个传感器节点的簇为例，其中每两个相邻的传感器节点进行编码协作，与簇头节点进行通信。这里假设完全协作（情况1），协作水平0.5β=。假设第1帧传输K bit信息，编码后码字长度为 /2N （两帧总长为N）（忽略循环冗余码校验（Cyclic Redundancy,CRC）校验位长度），则总能耗为

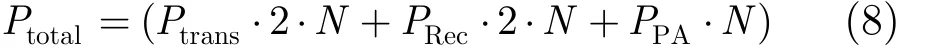
6 仿真结果与分析

本节研究了所提算法的性能。首先仿真了所构造码字的文字差错率（Word Error Rate, WER）性能。实验中，分别仿真了（3,9,3,6）规则根校验全分解 LDPC码与非规则根校验全分集 LDPC码的性能，码字的校验矩阵结构如图6所示，码率分别 Rc=1/3和 0.45。非规则码字多项式分布 （ λ1（x ） ,ρ1（x）,λ2（ x ） ,ρ2（x）） 表示为

实验中，采用 BPSK调制，噪声 zi～N （ 0,σ2）,σ2=N/2，信道的衰落α 服从独立的瑞利分布，0j译码采用BP迭代译码算法，最大迭代次数50次。每次重传的码字长度一样 N = 6 000，信息长度K= 2 000，同时还比较了一同样码率的随机LDPC码性能。 其BER性能如图8，图9所示。

同时为了比较所提编码方案与简单 LDPC编码，以及自动发送请求（Automatic Repeat Request,ARQ）方案的能效，仿真了达到不同BER时，传输每比特信息能效。采用 MATLAB软件进行仿真，网络的仿真环境为：100个初始能量为0.5 J的传感器节点随机地分布在半径为100 m的圆形区域内，Sink节点在圆心处，仿真网络参数如表1所示。

图10显示了当WER为 1 0-3时，未编码传输方案、采用文献[17]方法构造的随机 LDPC码编码方案、ARQ随机LDPC编码方案和本文构造的非规则根校验LDPC码编码方案传输单位比特的能耗，从图中可以看出，未编码方案，在噪声功率较低时，能耗较低，随着噪声的增加，需要显著地增加发射功率来达到特定的WER，应用FEC编码后，则噪声门限大大提高，而且随着噪声的增加，成功传输每比特消耗的能耗增加缓慢，即在信道条件较差的环境，本文构造的码字性能更优。图11给出了达到误比特率为10-4时，能耗对比情况，得到与图10相同的结论，只是，此时噪声门限要比图10低。

表1 网络的其它参数设置

从图 10，图 11中可以看出，当信道噪声较小时，不用 FEC编码或者用一些冗余度低的简单编码，反而更节能；当信道条件差时，需要利用纠错能力强的编码。因此，需要在FEC的可靠性所带来的能量节省与 FEC编解码能耗和冗余度之间寻找一个平衡。

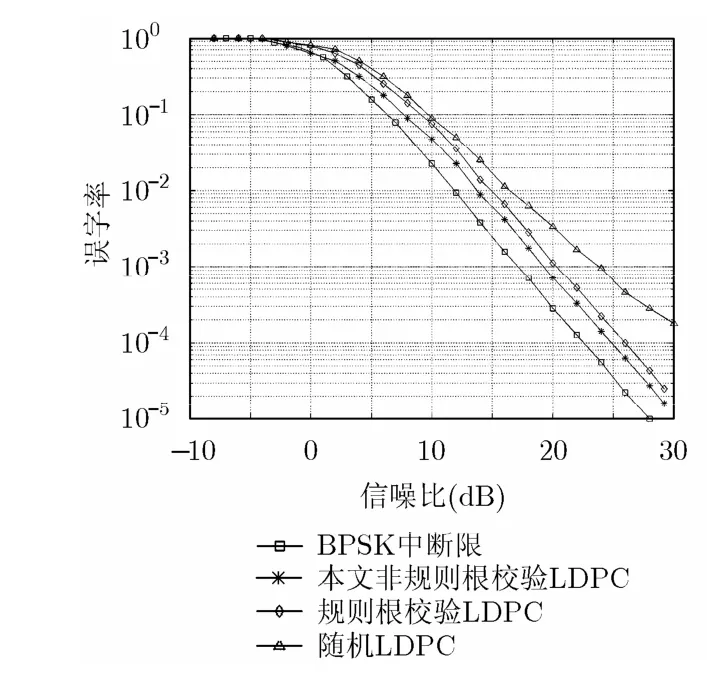
图8 不同码字性能比较（Rc=1/3）

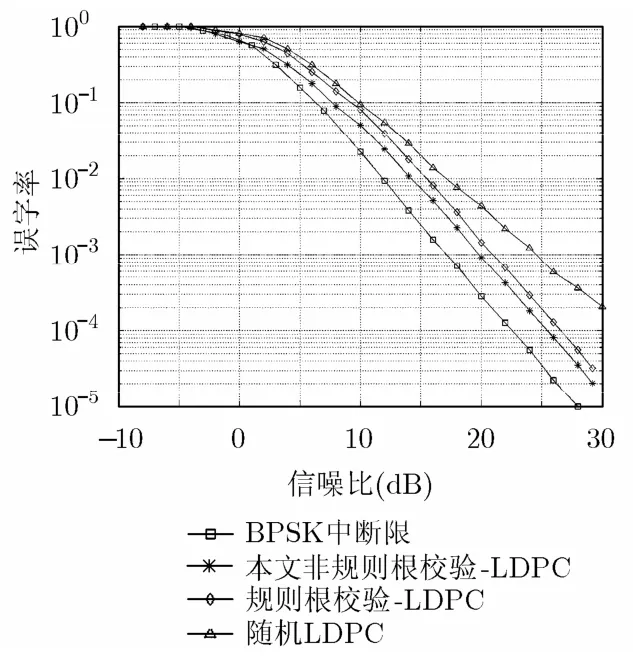
图9 不同码字性能比较（Rc=0.45）

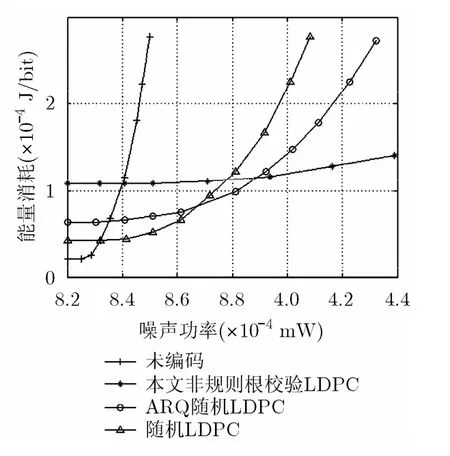
图10 各种传输方案能耗 （ WER=10-3）

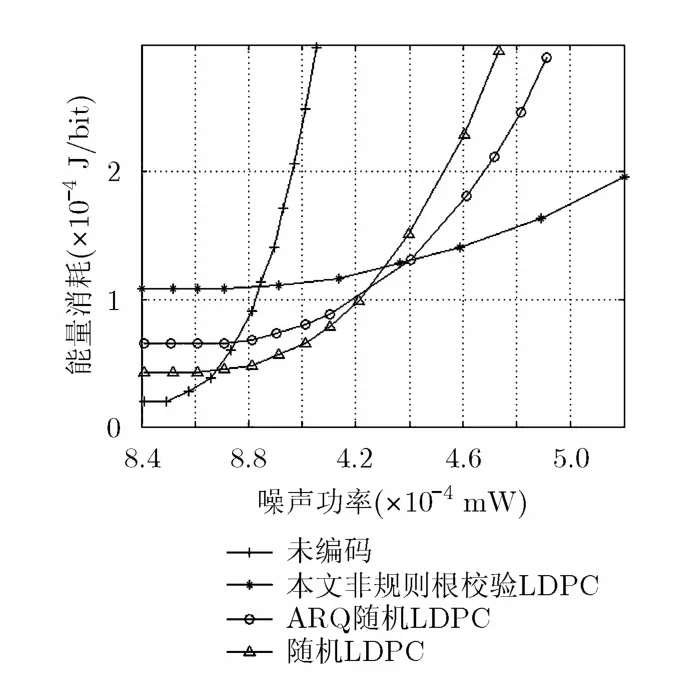
图11 各种传输方案能耗图（WER= 1 0-4）

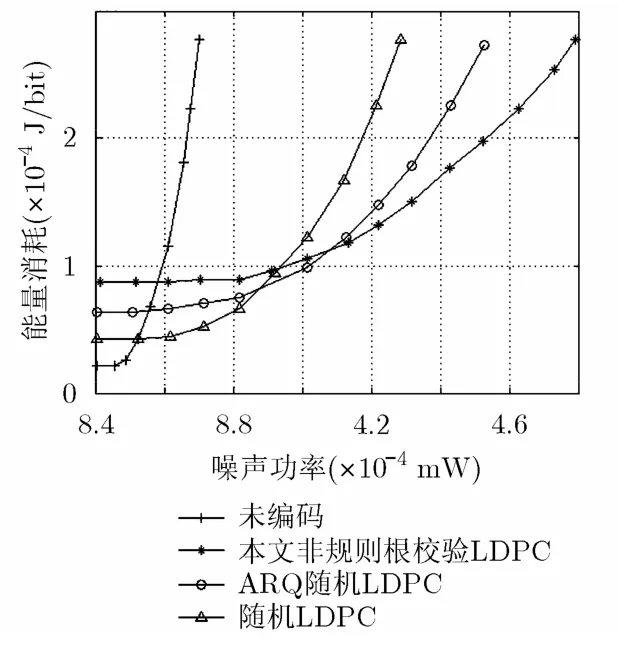
图12 源-目的信道与协作信道不同噪声性能 （ BER= 1 0-4）

图13 源-目的信道与协作信道 不同噪声性能 （ BER=10-3）

为了验证本文提出的基于根校验全分集 LDPC码在对抗某一链路突然恶化时的优势，本文仿真了源节点-目的节点信道，与协作中继信道经历不同噪声影响时的能效，假设协作信道上噪声比源-目的信道的噪声小（小 0 .5×10-4mW ）。图 12，图 13采用文献[17]方法构造的随机LDPC码编码方案，ARQ随机 LDPC编码方案和本文构造的非规则根校验LDPC码编码方案能量消耗比较。可以明显看出，采用本文所提全分集根校验 LDPC码能够降低能耗。这是因为基于根校验全分集LDPC的编码方案中，信道条件较好的协作信道可以弥补源部分性能损失。

7 结束语

本文研究了分簇无线传感器网络中，基于全分集LDPC码的编码协作簇内通信方案，并给出速率容根校验全分集LDPC码的设计。以能效作为最终目标，给出了各种编码方案的能效分析，仿真结果表明，在信道条件较差的情况下，采用根校验全积分LDPC码能够降低无线传感器网络的能耗，提高网络的生命期。

[1] Sankarasubramaniam Y, Akyildiz I F, and McLaughlin S W.Energy efficiency based packet size optimization in wireless sensor networks[C]. Proceedings of the 1st IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 2003: 1-8.

[2] Yue J, Lin Z, Li J, et al.. Unequal error protection distributed network-channel coding based on LT codes for wireless sensor networks[C]. Proceedings of the IEEE Wireless Communications and Networking Conference （WCNC）,Shanghai, China, 2013: 1482-1487.

[3] Jafarizadeh S and Jamalipour A. Data persistency in wireless sensor networks using distributed luby transform codes[J]. IEEE Sensors Journal, 2013, 13（12）: 4880-4890.

[4] Yue J, Lin Z, Vucetic B, et al.. The design of degree distribution for distributed fountain codes in wireless sensor networks[C]. Proceedings of the IEEE International Conference on Communications （ICC）, Sydney, Australia,2014: 5796-5801.

[5] Qassim Y and Magana M E. Error-tolerant non-binary error correction code for low power wireless sensor networks[C].Proceedings of the International Conference on Information Networking （ICOIN）, Phuket, Thailand, 2014: 23-17.

[6] Yue J, Lin Z, Vucetic B, et al.. Performance analysis of distributed raptor codes in wireless sensor networks[J]. IEEE Transactions on Communications, 2013, 61（10）: 4357-4368.

[7] Rahhal J S. LDPC coding for MIMO wireless sensor networks with clustering[C]. Proceedings of the International Conference on Digital Information and Communication Technology and it's Applications （DICTAP）, Bangkok, Thailand, 2012:58-61.

[8] Kissling C and Clazzer F. LDPC code performance and optimum code rate for contention resolution diversity ALOHA[C]. Proceedings of the IEEE Global Communications Conference, Atlanta, GA, USA, 2013: 2932-2938.

[9] Boutros J J, Guillen I, Fabregas A, et al..Low-density parity-check codes for nonergodic block-fading channels[J]. IEEE Transactions on Information Theory, 2010, 56（9）: 4286-4300.

[10] Lechner G, Nguyen K D, Guillen I, et al.. Optimal power control for LDPC codesinblock-fading channels[J]. IEEE Transactions on Communications, 2011, 59（7）: 1759-1765.

[11] Healy C T and Lamare R C D. Full diversity LDPC codes with a reduced structure for general block fading channels[C].Proceedings of the Tenth International Symposium on Wireless Communication Systems, Ilmenau, Germany, 2013:1-5.

[12] Paola P, Gianluigi L, and Marco C. Unequal diversity LDPC codes for relay channels[J]. IEEE Transactions on Wireless Communications, 2013, 12（11）: 5646-5655.

[13] Tian Z. Distributed space-time coding with decode-and-forw ard-amplify-and-forward selection relaying protocol in coope rative wireless sensor networks[J]. IET Wireless Sensor Systems,2013, 3（1）: 9-15.

[14] Hunter T E, Sanayei S, and Nosratinia A. Outage analysis of coded cooperation[J]. IEEE Transactions on Information Theory, 2006, 52（2）: 375-391.

[15] Balakrishnan G, Mei Y, Yingtao J, et al.. Performance analysis of error control codes for wireless sensor networks[C].Proceedings of the Fourth International Conference on Information Technology, Las Vegas, NV, USA, 2007: 876-879.

[16] Xiao H and Banihashemi A H. Improved progressive-edgegrowth （PEG） construction of irregular LDPC codes[J].IEEE Communications Letters, 2004, 12（8）: 715-717.

[17] MacKay D J C. Source code for progressive edge growth parity-check matrix construction[OL].http://www. Available:phy.cam.ac.uk/Mackay/PEGECC. html, 2010.