径向位移对井壁稳定性影响的分析方法

祁斌，陈平，夏宏泉，涂君君

（1．油气藏地质及开发工程国家重点实验室 西南石油大学，四川 成都610500；2．巴中市发展和改革委员会，四川 巴中636000；3．西南油气分公司油地处，四川 成都610016；4．西南油气分公司工程监督中心，四川 德阳618000）

0 引 言

在油气井井壁稳定性分析方面，研究钻井液液柱压力与地层三压力之间平衡关系的方法很多，而研究地层岩石弹性载荷及径向位移和井壁稳定性之间的定量分析方法却很少见。未钻开前地层岩石只受到原地应力作用。当地层被钻开后，井壁在受到原地应力作用的同时还受到人为因素产生的附加应力作用［1］。实践证明，钻井过程中井壁岩石只发生微小弹性形变，可采用线性叠加原理进行井壁受力分析。本文将加载在井壁上的应力分为2个部分，一部分来自原地应力，另一部分来自外界因素产生的附加应力场，如钻井液液柱压力、抽提或激动压力等产生的附加应力；逐次分析后，采用叠加原理判断总应力作用下的井壁岩石稳定特性［2］；从钻井时地层岩石应力分布特征着手，在一定假设的前提下，借助测井资料建立地层岩石弹性极限载荷和井壁径向位移计算模型，并开展两者关系研究，用以评价地层岩石力学特性与井壁稳定性的关系，为钻井工程提供参考和指导依据。因原地应力引起的井壁应力分布计算模型已完备，本文重点开展外界因素引起的井壁应力变化对井壁位移影响的研究。

1 应力场模型的建立

1．1 附加应力场模型建立

假设井筒半径为a，地层压力为pp，由外界因素产生的井筒内附加应力场Q为

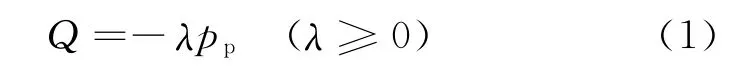
式中，负号表示该应力场指向井壁；λ为引入的地层载荷系数，是附加应力与地层压力的比值，用来描述地层承载附加应力的能力。式（1）之所以用地层压力pp描述，一是为了在后续公式推导中强调真实地层条件下各种客观因素对井壁岩石应力分布特征影响；二是在实际应用中减少经验参数的个数，提高计算精度和可靠性。井筒内应力场分布特征服从边界条件

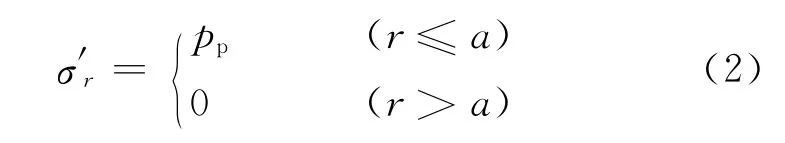
式中，σ′r为附加应力产生的井筒径向应力，MPa；r为地层到井轴的距离，cm。

根据上述假设，附加应力是钻井液液柱压力、抽提或激动压力等钻井施工过程中人为因素产生的各种压力的综合反映［3］。在利用平衡方程、几何方程和本构方程求解时，只需求得径向应力、周向应力和井壁径向位移的解即可［4］。其解为

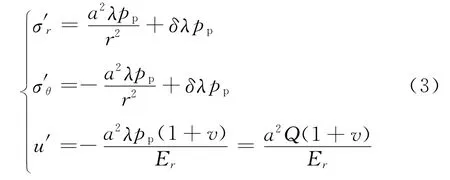
式中，σ′θ为附加应力产生的周向应力，MPa；u′为井壁径向位移，cm；E为弹性模量，MPa；v为泊松比。

1．2 原地应力场径向位移模型的求解

在原地应力平衡方程、本构方程和相应边界条件给定的情况下，结合几何方程求取直井井壁径向位移［5］，其解为

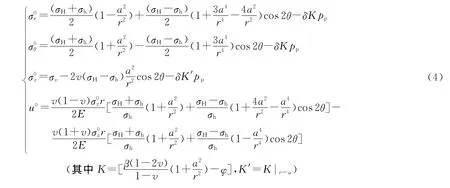
式中，u0为原地应力引起的径向位移；σ0r和σ0θ分别为原地应力引起的井壁径向、周向应力，MPa；在渗透性地层δ＝1，非渗透性地层δ＝0；β为有效应力系数（Biot系数）；σH、σh分别为最大、最小水平地应力，MPa；θ为井周方位角，（°）。

由于井壁岩石为小变形弹性体［6］，根据线性叠加原理，井壁上的总径向和周向应力为

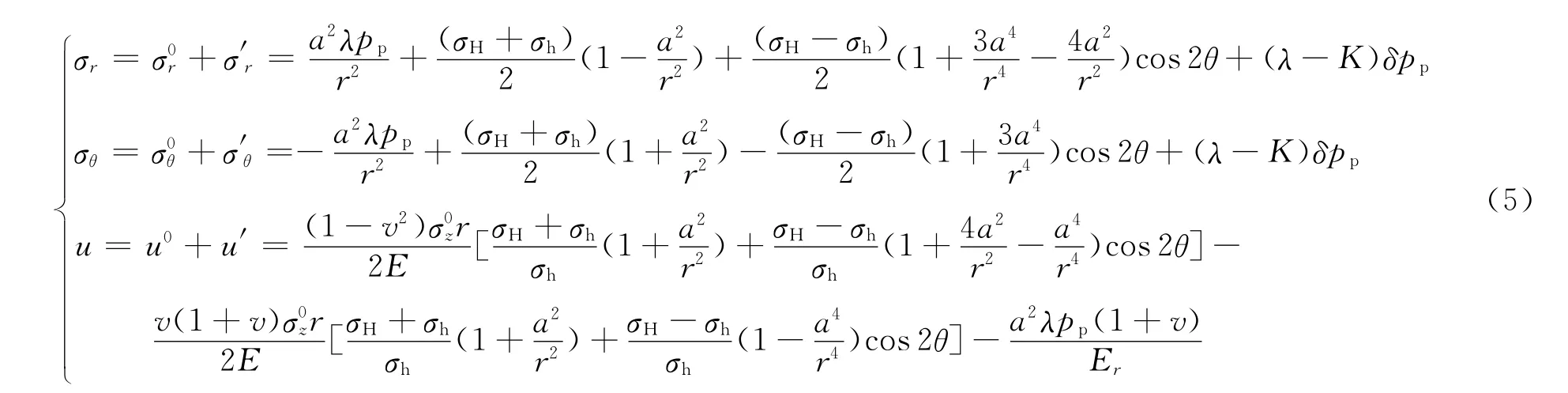
式中，σr和σθ分别为井壁径向、周向总应力，MPa；u为总应力作用下的井壁径向位移，cm。

2 井壁稳定性分析中关键参数计算

2．1 弹性极限载荷系数的计算

根据Mohr－Coulomb准则，岩石破坏时有

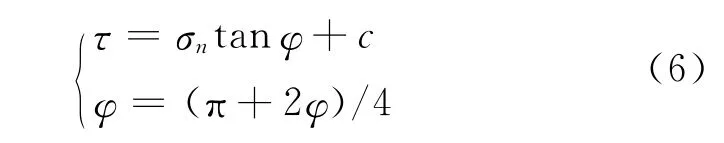
式中，τ为岩石剪切强度；σn为岩石所受剪应力；φ为岩石内摩擦角；c为岩石内聚力。

根据井壁岩石应力分布特征［7］，在r＝a时，井壁上的径向和切向总应力为

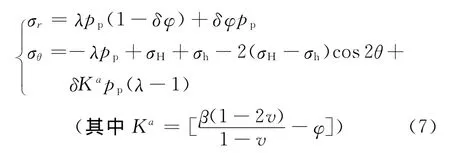
当δ＝0时，将式（7）相关参数代入式（6），有

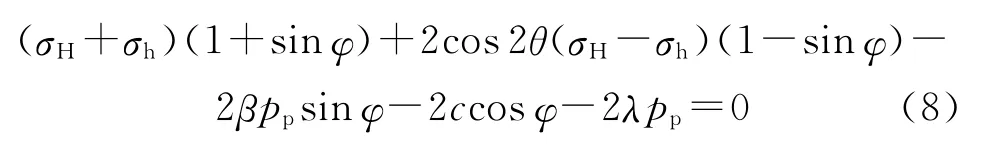
因此，最先在井壁处r＝a发生剪切破坏时，有

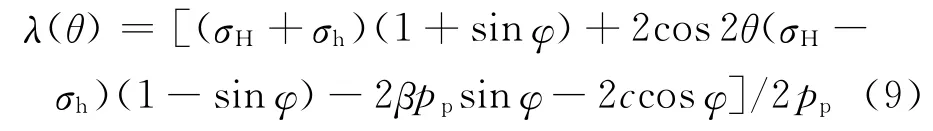
对于同一深度地层，式（9）中的弹性载荷系数λ只是井周方位角θ的函数，其他相关参数都是源自地层条件下岩石所受的应力分量和岩石固有特性参数［8］。当θ已知时，可获得该方位的弹性极限载荷系数λe，当λ≤λe时，地层永远处于弹性状态，而不发生剪切破坏。在θ＝90°和θ＝270°处，井壁弹性载荷系数最小，承受附加应力的能力较弱，该方位易发生剪切破坏。在钻井过程中，为防止因剪切破坏引起的井壁失稳，一定要保持井筒压力与地层压力的比值小于θ＝90°和θ＝270°处井壁的弹性载荷系数。

在同一深度地层弹性载荷系数λ只与井周方位角θ有关，式（9）可改写为

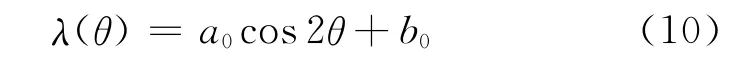
式中，a0、b0为常数。

2．2 径向位移的计算

当r＝a和δ＝0时，将式（9）代入式（5），可以得到径向位移计算式

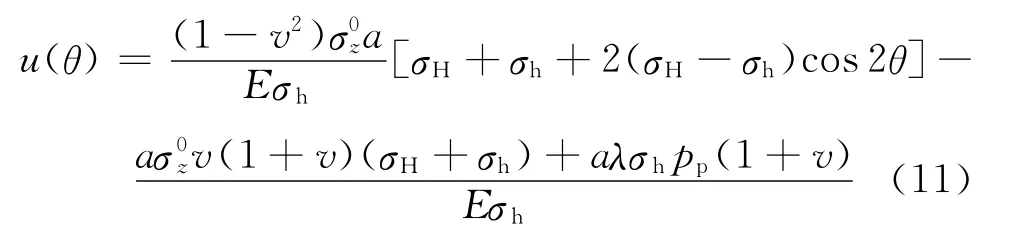
式中，径向位移为负，表示井壁产生径向弹性形变指向井壁。径向位移的大小与弹性载荷系数成正比，这也表明，当λ≤λe时，采用同一密度（弹性载荷系数不变的情况下）钻井液对某段地层钻进时，弹性极限系数较小的地层径向形变较大，易发生剪切破坏；弹性极限系数较大的地层径向形变较小，不易破坏。同理，对同一深度地层该式也可表示为

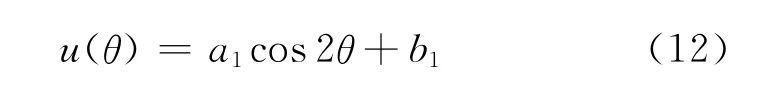
式中，a1、b1为常数。

3 应用实例分析

基于上述计算模型，开展蓬莱地区蓬莱2井须家河组地层附加应力场与井壁稳定性分析。根据该井须家河组的测井资料计算地层泊松比、弹性模量、抗压强度、抗剪强度、地层压力和水平主应力，并将这些数据代入式（9）和式（11），计算承受附加应力的能力较弱，易发生剪切破坏的θ＝90°和θ＝270°处的地层弹性极限载荷系数及弹性状态下的最大径向位移，分析钻井过程中附加应力场对井壁稳定性影响，确定附加应力上限值。

经对计算结果分析，蓬莱2井的地层弹性极限载荷系数与极限径向位移成幂增长正比关系（见图1），弹性极限载荷系数上限基本自上到下依次增大（见图2）。首先，该段地层弹性载荷系数最大值为2．02，最小值为1．54，钻井时为确保井壁稳定性，整个井段的附加应力与地层压力的比值应小于1．54，否则井壁进入塑性形变，当附加应力场激动时易失稳。其次，当地层弹性载荷系数大于1．82（径向位移为0．46cm）时，径向位移易发生突变，导致部分井段扩径。因此，在该井钻进或下钻过程中，需保证附加应力场与地层压力的比值小于1．54，以防压力激动导致部分井段发生塑性形变或失稳。

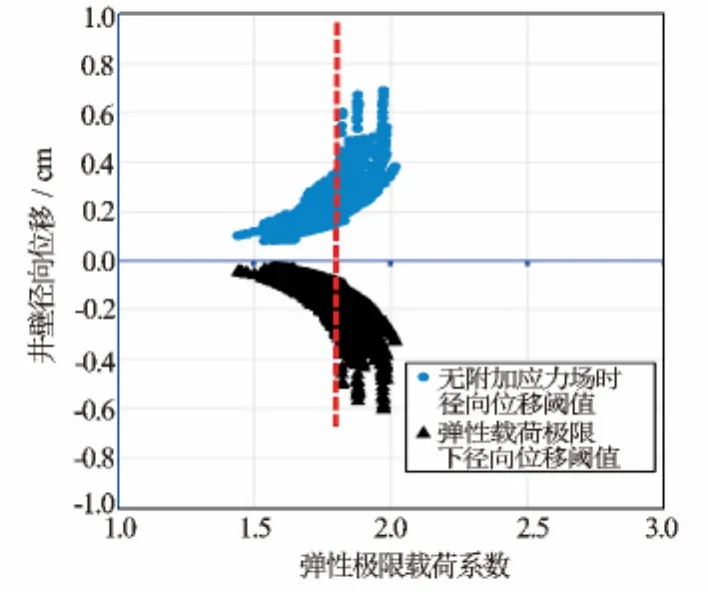
图1 弹性载荷系数与径向位移关系

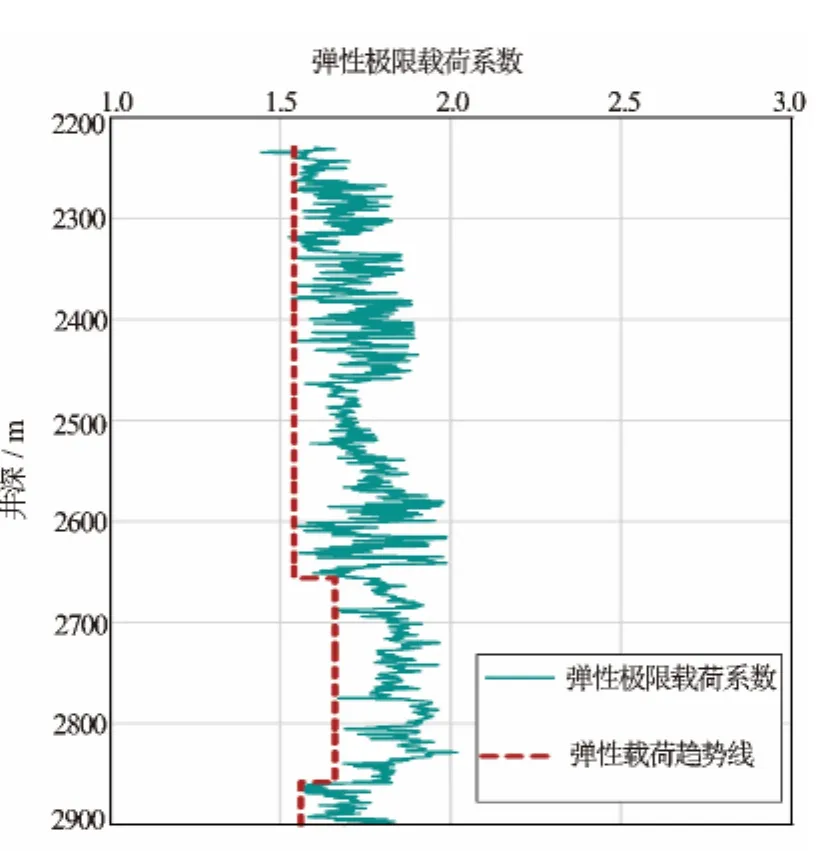
图2 地层弹性极限载荷系数

图3中，地层2656m段以上地层径向位移下限偏小，附加应力场的激动很容易使该段地层产生大于径向位移下限的塑性形变而导致井壁失稳；而2656～2858m地层径向位移下限偏大，井壁抗压力激动能力较强，不易失稳。现场施工证明2656m以上地层扩径要比其以下地层严重。同时，该井径向位移最大值为0．76cm、最小值0．12cm，其中径向位移较大值出现在2242～2458m须五段和2570～2642m须三段，该类层段岩性主要是泥岩，并伴有少量砂岩硬夹层，其中泥岩地层的径向位移要大于砂岩地层（见图3）。径向位移差异的存在，易引起两者的接触面滑动，导致井壁坍塌掉块进而扩径。实践证明，在该类地层确实存在井壁掉块扩径或下钻遇阻现象。

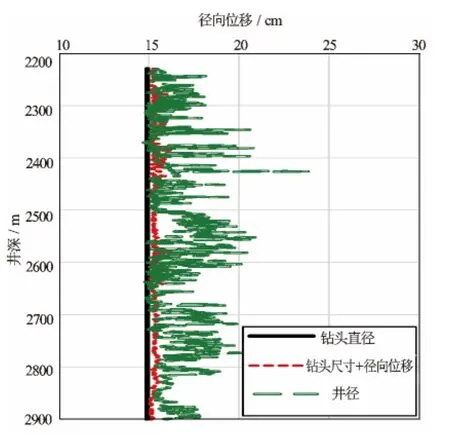
图3 地层极限径向位移与井径对比

4 结 论

（1）引入弹性载荷系数建立了直井井筒内附加应力场计算模型，并结合直井井壁围岩应力分布模型和摩尔－库伦准则得到了井壁弹性载荷系数和径向位移计算方法，利用该方法可得到原地应力条件下地层的弹性极限载荷系数和最大径向位移。

（2）在井筒同一深度θ＝90°和θ＝270°方位处，弹性载荷系数和径向位移出现极小值，说明该方位井壁承受附加应力的能力最弱，井壁抗压力激动能力差，应以该方位的弹性载荷系数和径向位移上限作为参考，设计合理的钻井液密度。

（3）蓬莱2井的地层弹性极限载荷系数上限值自上到下依次增大。该井段附加应力场激动时的最大应力与地层压力的比值应小于1．54，否则井壁发生塑性形变或失稳。当地层弹性载荷系数大于1．82（径向位移为0．46cm）时，径向位移易发生突变，导致井壁失稳扩径。该井须家河组2656m以上地层径向位移下限偏小，附加应力场的激动很容易使该段地层产生大于径向位移下限的塑性形变而导致井壁失稳；2656～2858m段地层径向位移下限偏大，井壁抗压力激动能力较强，不易失稳。同时，泥岩与砂岩硬夹层径向位移差异较大，易引起两者的接触面滑动，导致井壁掉块扩径或下钻遇阻。

（4）径向位移在地层稳定性趋势分析方面具有较好的应用效果，但该数值相对较小，在定量评价方面尚需进一步完善。

［1］殷有泉．岩石力学与岩石工程的稳定性［M］．北京：北京大学出版社，2011，3：28－44．

［2］祁斌，夏宏泉．塔里木奥陶系地层应力计算方法研究［J］．测井技术，2008，32（6）：553－555．

［3］王珂，戴俊生．地应力与断层封闭性之间的定量关系［J］．石油学报，2012，33（1）：74－78．

［4］王连捷，孙东生，林为人，等．地应力测量的非弹性应变恢复法及应用实例［J］．地球物理学报，2012，55（5）：1674－1677．

［5］魏周拓，范宜仁，陈雪莲，等．横波各向异性在裂缝和应力分析中的应用［J］．地球物理学进展，2012，27（2）：218－224．

［6］Matsuki K．Anelastic Strain Recovery Compliance of Rocks and Its Application to In－situ Stress Measurement［J］．Int J Rock Mech Mining Sci，2008，45（6）：1－7．

［7］Tang C A，Hudson J A．Rock Failure Mechanisms—Explained and Illustrated［M］．London：Taylor and Francis，2010：20－32．

［8］JAEA．Final Report on the Surface－based Investigation（phase 1）at the Mizunami Underground Laboratory Project［R］．2007：17－28．