频率域地－井垂直电磁法响应特征数值模拟

王智，潘和平，骆玉虎

（中国地质大学（武汉）地球物理与空间信息学院，湖北 武汉430074）

0 引 言

井间电磁勘探方法广泛应用于油气勘探领域，但金属套管井限制了井间电磁法横向探测范围［1］，目前最大探测距离不超过1km。地－井电磁法能达到4km半径的勘探范围，但也只能识别油水平面展布，难以精细分辨储层纵向变化［2－3］。地－井电磁法是另一种具有潜力的方法，国内外对地－井电磁法的研究比较少，Augustin［4］、Wilt等［5］曾对地－井电磁法圈定油气藏进行了数值模拟研究；魏宝君等［6］进行了地－井电磁系统成像研究，均取得了一定效果。但是，传统地－井电磁法横向分辨率低，受近地表强电磁场耦合干扰严重，使该法的应用受到限制。张荣锋等提出固定井源距垂直电磁剖面地井电磁成像方案，但其分辨率和勘探范围依然有限［7］。李静和等［7］提出地－井垂直电磁 Walkaway剖面法（地面激发、接收装置固定在井孔中，得到以接收点垂直位置为纵坐标，以不同频率点或者趋肤泛围为横坐标的测深剖面，称为地－井垂直电磁剖面），主要采用积分方程法对模型进行模拟研究。

电磁法数值模拟主要有3种方法：有限差分法［8－9］、有限单元法［10－11］和积分方程法［12］。有限差分法是用差商代替微商，将待求解的连续微分方程变换为离散的差分方程，通过求解差分方程得到原微分方程的近似解；有限单元法是一种求解场的变分问题的数值方法，通过变分原理，等价变换成变分方程；积分方程法是从场参数（场强或场位）所满足的微分方程边值问题出发，通过某些变换导出有关参数（场强、位、积累电荷密度或散射电流密度）所满足的积分方程，用近似计算方法求积分方程的数值解。

积分方程法只需对异常体进行剖分和求积，不必计算整个区域的场，不涉及微分方程法中的吸收边界等复杂问题。该方法存在对复杂模型的适应性差、方法的精确度严重依赖于系数矩阵的精度以及系数矩阵的精度往往无法保证等缺点。有限元法推导过程相对简单，对于变分问题自然边界条件已经隐含地得到满足，只需考虑强边界条件，在处理复杂的几何形状时适应性好。本文针对频率域地－井垂直电磁法，应用有限元法对不同的模型进行模拟研究，通过模拟均匀介质背景下相对高电阻率与低电阻率条件下目标体的异常特征，分析和讨论了模型参数变化、不同埋深、异常体与收发位置关系变化时的电磁响应特征和规律，为了解与研究地－井垂直电磁法的探测能力提供参考。

1 频率域地－井垂直电磁有限元法基本原理

1．1 工作方法

在井中（沿z方向）从浅至深一定范围内按一定间距布设电场接收装置，在地面井口处布设激发场源，激发频率（1～1000Hz）从高频至低频扫描，以位于不同深度的井中测点为纵轴刻度，以频率为横轴，可获得1张垂直电磁剖面［13］。

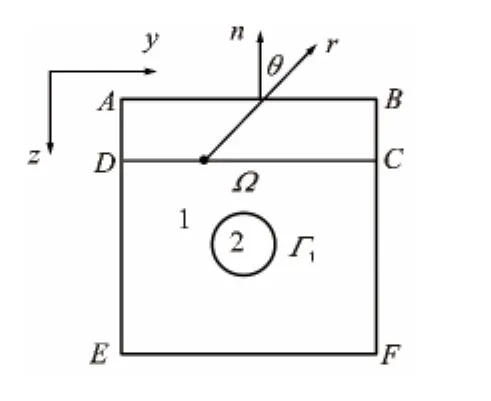
图1 研究区域

1．2 基本原理

假定地下电性结构是二维，将原点取在地面上，平行于走向方向为x轴，垂直方向为y轴，垂直向下方向为z轴，外加源的方向为x方向，此时只存在不随走向而变的x方向的电场（见图1）。取外边界足够大，所包围的区域为Ω，使局部不均匀体的异常场在外边界上为0。图1中，圆圈为局部异常体，Γ1为异常体的边界，r为电磁波的传播方向，n为外边界的外法向方向，θ为r与n的夹角。从麦克斯韦方程组出发得到的有源电磁场的边值问题为

边值问题的式［1（b）］、式［1（c）］为内边界条件，分别表示在介质分界面上电场和磁场的切向分量连续。式［1（d）］为计算区域截断边界即外边界条件，是由电磁波的传播方程u＝u0e－kr求导后与传播方程两边分别乘以k后相加得到的。其中，r为源到边界上任一点的距离，k为空气中的波数时，k0＝和η0分别为空气中的介电常数和磁导率；当k为地层中的波数时和μ分别为地层中的介电常数和磁导率。对于电磁法，频率足够低，可忽略位移电流的影响，地层中的波数可写为

与式（1）中的边值问题等价的变分为

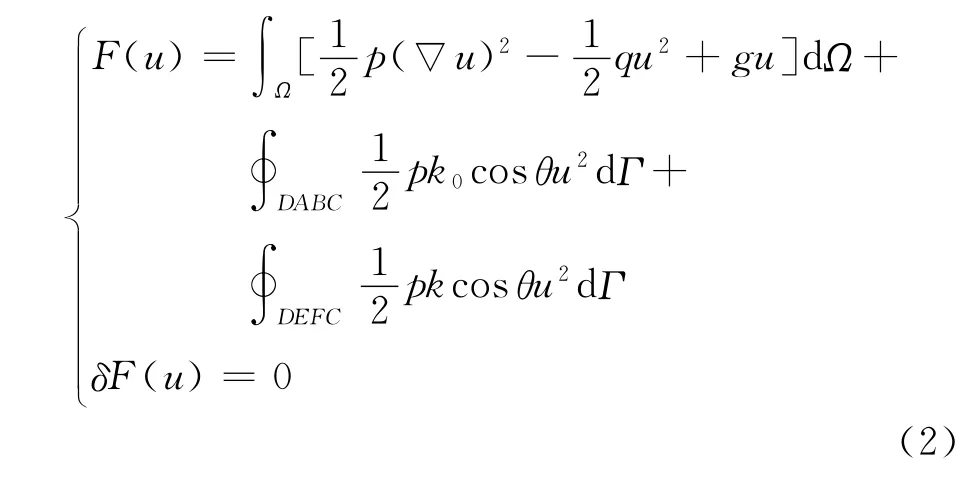
1．3 有限元法

区域Ω采用矩形网格剖分，利用双线性插值表示小单元内的场值（见图2），图2中1、2、3、4为小单元角点的编号，Dy、Dz分别为小单元的边长。

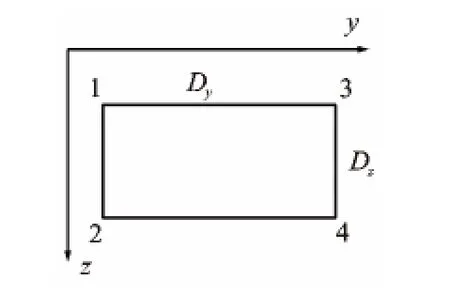
图2 网格剖分与小单元编号

单元中的场值u可用形函数表示为

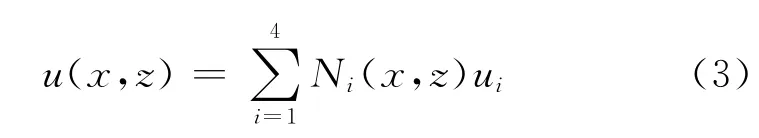
将式（3）代入式（2），经整理可得到方程

插值所用的形函数以及K1e、K2e、P、K4e、K5e系数矩阵的数值请参考文献［14］。

将K1e、K2e、P、K4e、K5e扩展成全体结点的矩阵并对式（4）取变分

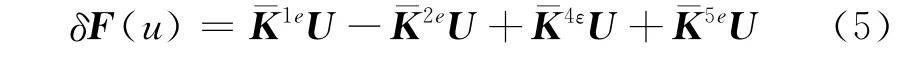
令式（5）为0可得线性方程组KU＝P，U为电场矢量；P为源项。解方程组，即可得到各节点的电场值。

1．4 线性方程组求解

BICGSTAB算法的主要思想是基于双边Lanczos算法和基于残差正交子空间的迭代算法［15］。预处理矩阵M采用不完全LU分解。一种不完全LU分解是指把A分解为¯L和¯U，它们对应的元素与L和U对应的元素相同，但2个因子分别于A的下、上三角部分有完全相同的非0结构。这种分解就是无填充的不完全LU分解，记为ILU（0）［15］。

1．5 压缩存储总体系数矩阵

用有限元方法作数值模拟时，由小单元集成后所有节点的总体系数矩阵是一个大型稀疏矩阵，包含了大量的0元素，网格节点越多，0值也越多。结合稀疏矩阵的特点选用较为常用的CSR存贮格式。

2 频率域地－井垂直电磁法响应特征模拟

2．1 算法正确性的验证

在上述理论的基础上，编制了相应的程序。为了验证程序的正确性和有效性，本文利用均匀半空间的解析解与数值解对比进行验证。

对于均匀半空间，供电电源为线源，在地面的观测场为

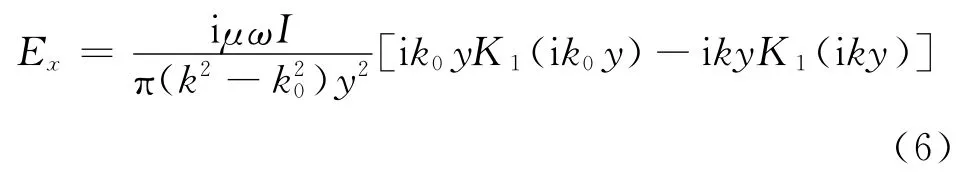
式中，K1（z）为第二类一阶变形的虚宗量贝塞尔函数；k为地层中的波数；k0为空气中的波数；y为偏移距；ε和μ分别为地层中的介电常数和磁导率。图3中均匀半空间的电阻率值为100．0Ω·m。图3（a）与图3（b）分别为f＝4Hz与f＝1024Hz时计算得到的电场值与解析解结果的对比，从2幅图中均可以看出数值解与解析解的结果十分接近，频率越高，边界条件越能减少边界的影响。这与文献［13］的结论一致。

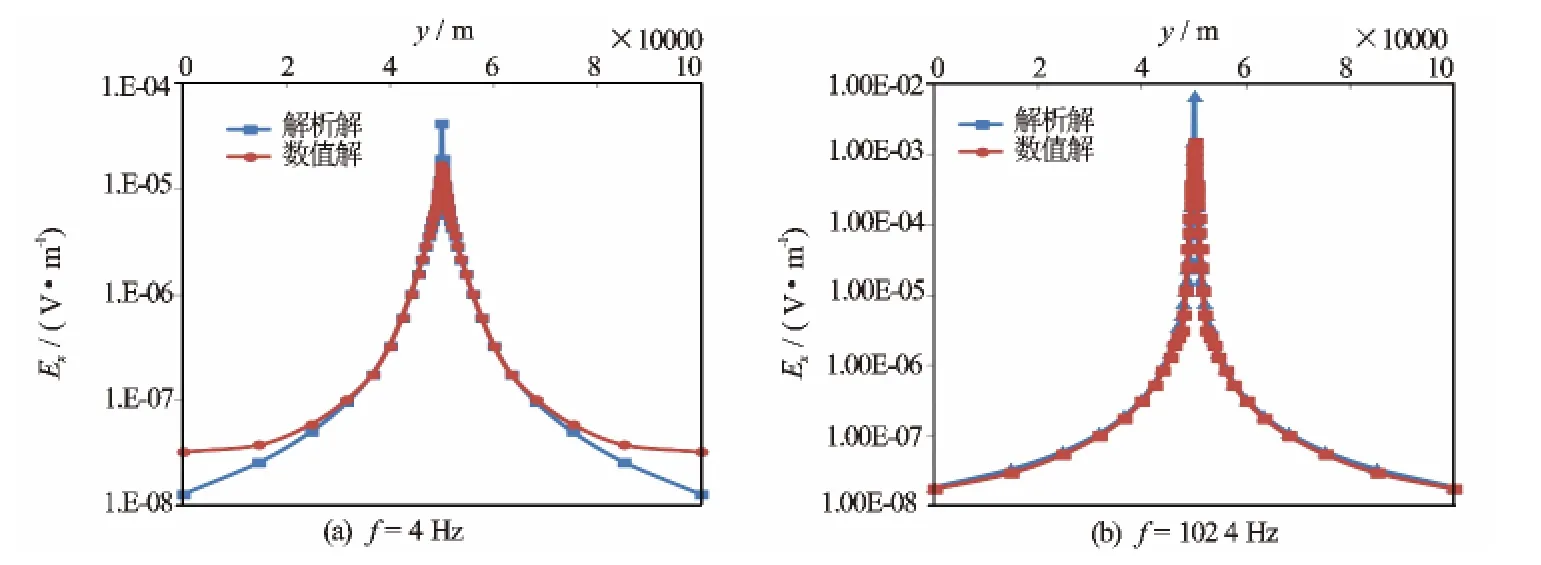
图3 均匀半空间下的电场数值模拟结果与解析解的对比

根据上述算法模拟均匀半空间条件下的频率域地井电磁法响应特征。本文模型将源置于中间网格一个节点上。选取参数：横向剖分时源所在位置附近的网格间距较小，向两侧逐渐加大，网格数为50；纵向方向网格，空中以较大的网格间距递增，向地层中先进行均匀剖分，均匀部分网格间距为20m，网格数为50，然后逐渐增大。所有模拟介质中，空气为不导电介质，电导率定为1．0×1012S·m－1。用上述有限元方法和网格剖分方式对勘探区均匀半空间中所赋存异常体进行模拟。结合地－井激电法的分析模式，从异常体性质、异常体与收发位置关系分析异常特征规律。

2．2 异常体性质对频率域地－井垂直电磁法的影响

2．2．1 均匀半空间中低电阻率异常体

埋深200m低电阻率异常体位于纵向11～16号节点之间，埋深400m低电阻率异常体位于纵向21～26号节点之间，低电阻率异常体电阻率为10Ω·m，围岩电阻率为100Ω·m。模型各项参数见图4，频率选择范围为20～212Hz，图5至图7是利用本文所述方法由低电阻率模型得到的正演模拟结果。

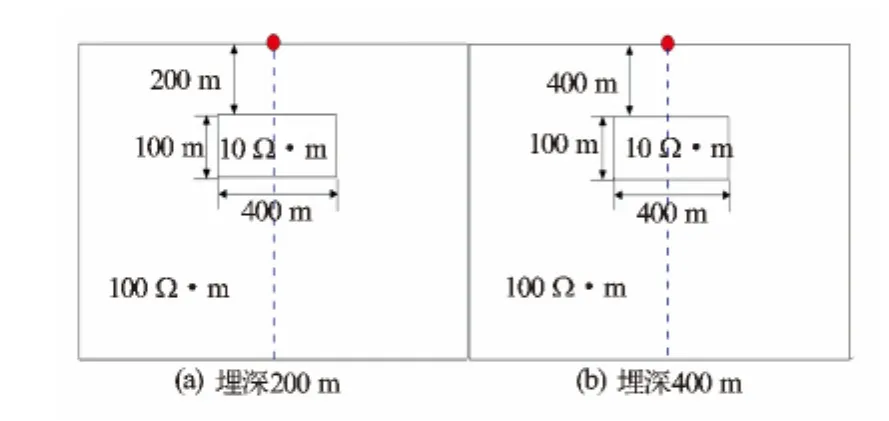
图4 低电阻率异常体模型

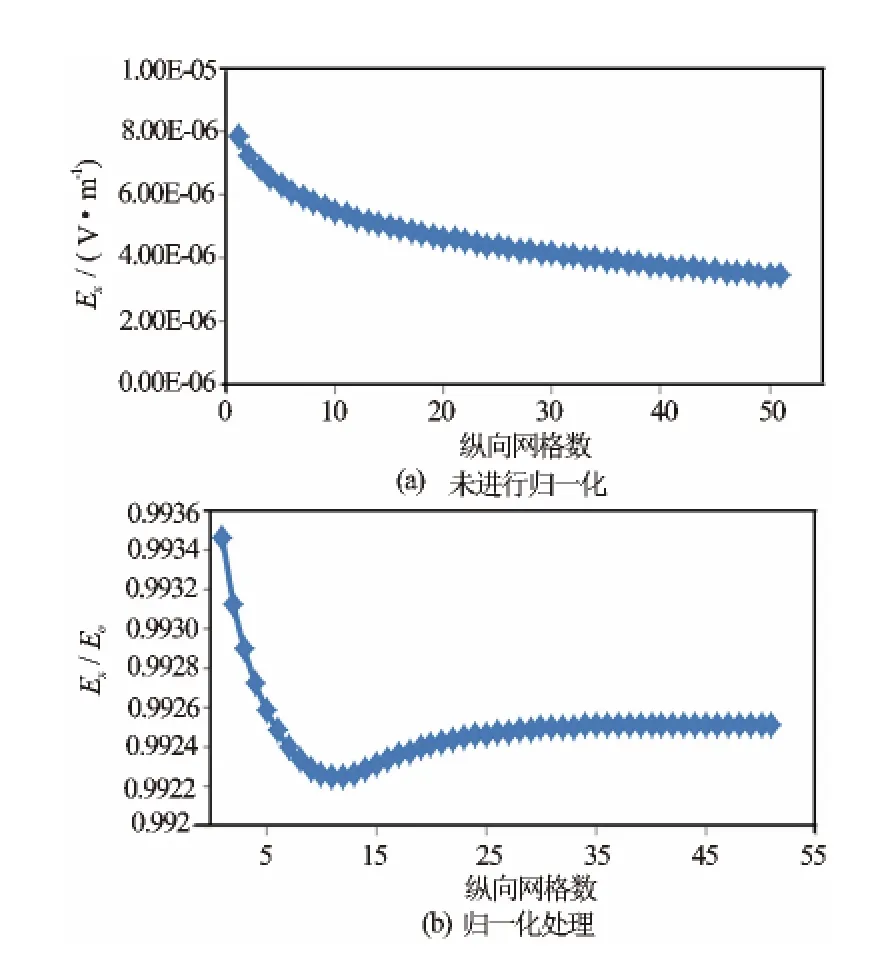
图5 频率1Hz正演模拟结果

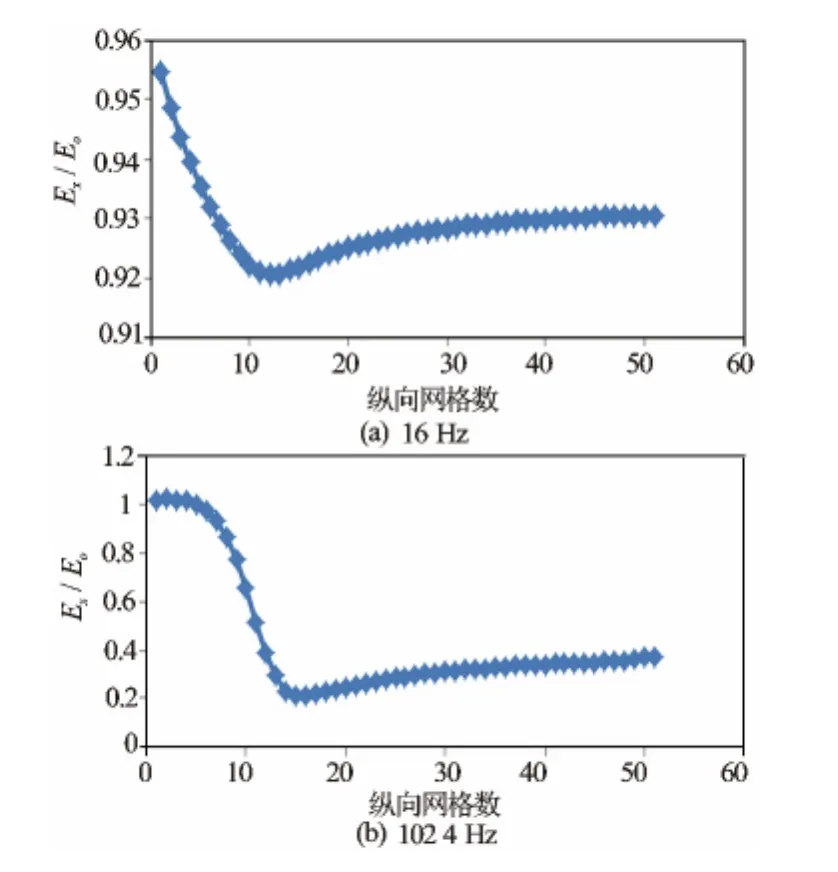
图6 不同频率下使用均匀半空间场归一化后正演模拟结果

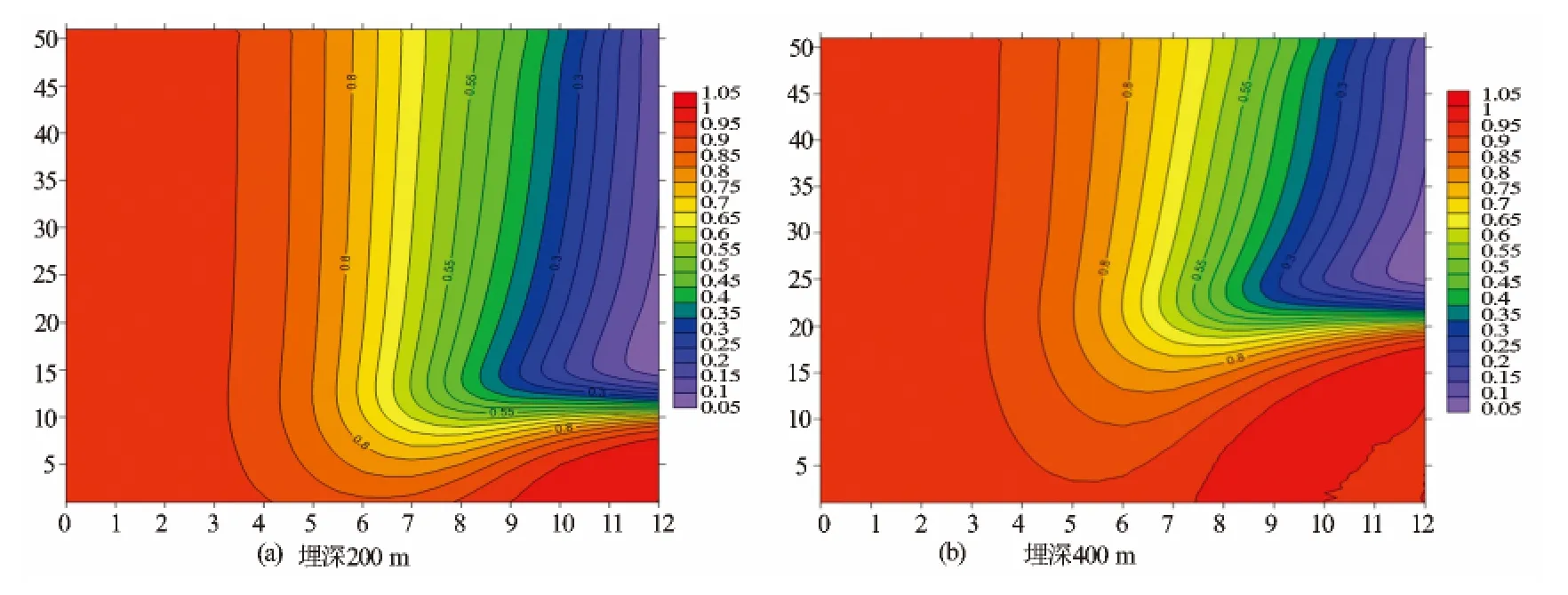
图7 均匀半空间电场归一化后的地电断面图

从图5（a）可以看出，场在源附近表现为较大的值，在纵向上，场值随着网格增大而减小，说明随着离开源的距离的增大，场在衰减，而在低电阻率异常体的11号网格附近，场值有不太明显的畸变，说明二次场相对于一次场值很小，异常的信息小，却依然包含在总场当中，为了对低电阻率体引起的电磁异常有较直观的了解，将不同频率产生的电场用均匀半空间的电场做归一化［14］，以突显纯异常引起的电场变化。正演结果图如图5（b）；从图6中可以看出，归一化后异常明显，随着频率的增加，异常极值逐渐向深部转移；图7为归一化后的电场地电断面图，以纵向网格数为纵轴，频率的对数为横轴。可以看到明显的异常，异常体附近等值线密集，在异常体周围呈现较低的电场值，低频反映异常的能力较弱。对于如此微小的异常能够在图7中反映出来，说明本文所述的方法对异常体的纵向分辨能力较强。由图7可以看出，本文所述的方法对不同的埋深的异常体的探测能力依然有效。

2．2．2 均匀半空间高电阻率异常体

高电阻率异常体位于纵向11～16号节点之间，电阻率为1000Ω·m，围岩电阻率为100Ω·m。模型各项参数如图8所示。

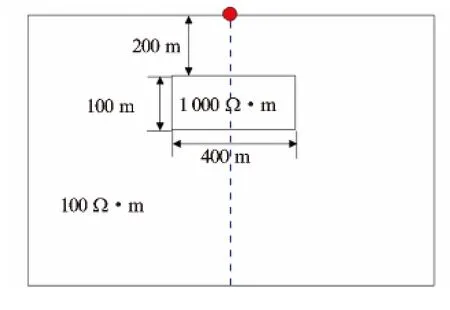
图8 埋深200m高电阻率异常体模型

图9为归一化后的地电断面图。从图9中可以看到明显的异常带，在异常体周围呈现较高的电场值，在高频段可以看到明显的异常，随着频率的增加，异常极值依然逐渐向深部转移，异常体附近等值线密集。对比图7（a）与图9，低电阻率异常体与高电阻率异常体在本方法中均能较好的反应出来，纵向分辨率较高，在高电阻率异常体模型中，能够较好反应异常体的频段范围，与低电阻率体相比较窄，约在27～212Hz。

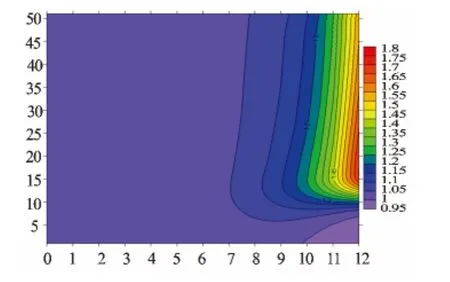
图9 均匀半空间电场归一化后电断面图

2．3 异常体与收发位置关系对频率域地－井垂直电磁法的影响

选取低电阻率异常体模型，各项模型参数图10，蓝色虚线分别代表井的不同位置。用上述有限元方法和网格剖分方式对异常体进行数值模拟。

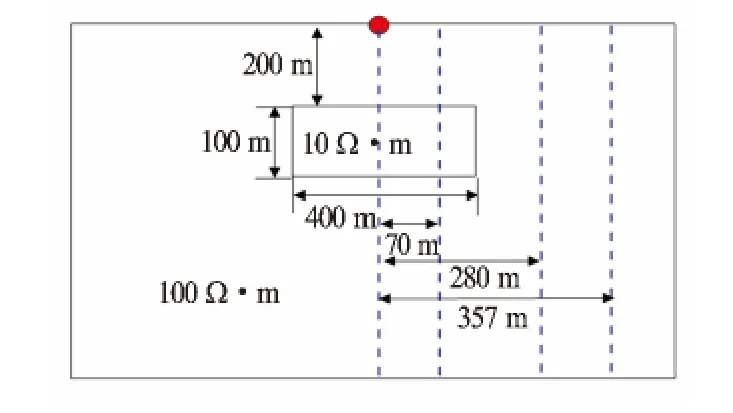
图10 埋深200m低电阻率异常体模型

图11为归一化后的地电断面图，可以看到较为明显的异常带，在异常体周围呈现较低的电场值，在高频段异常响应较强，随着频率的增加，异常极值依然逐渐向深部转移；对比图11（a）与（b），随着收发距的增加，异常体的异常响应越来越弱（归一化值往1靠近），异常等值线的密集带逐渐减稀疏，反应异常体的能力减弱，纵向的分辨率变差（见图11）。因此，在实际应用时要选择一个较小的收发距。

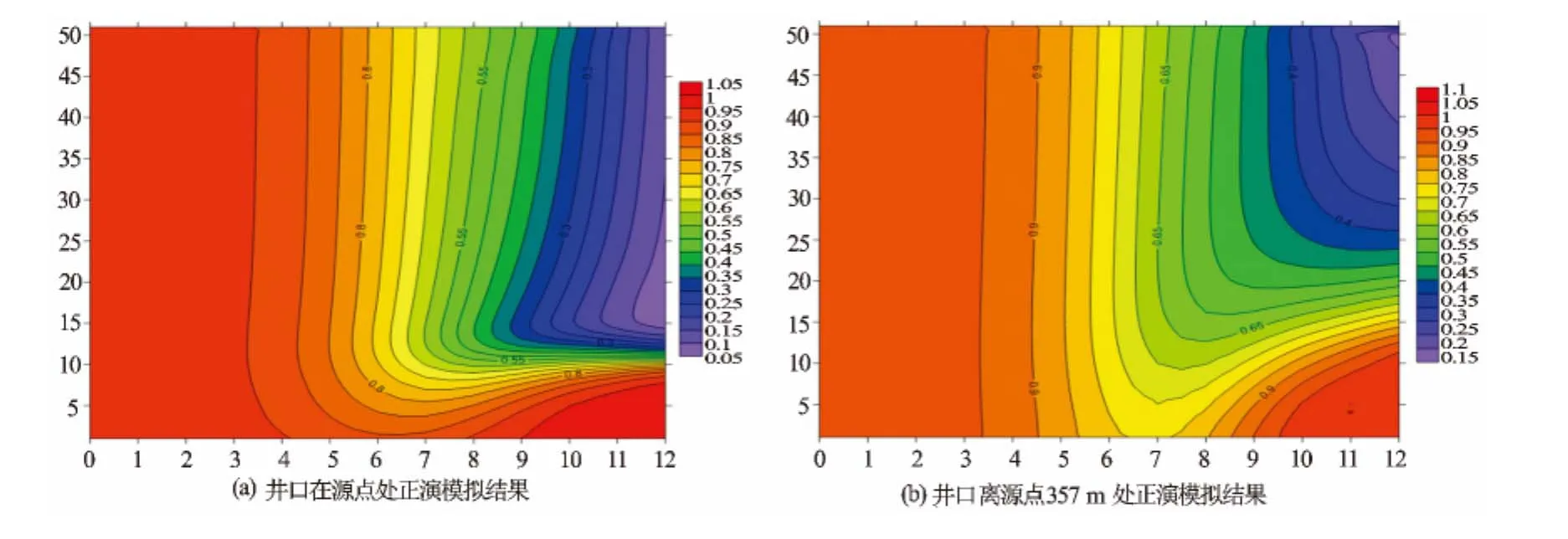
图11 归一化后地电断面图

3 结 论

（1）异常体的响应结果在图中都表现较为明显，说明了正演算法的有效性和正确性，算法中引入压缩存储数组，减少了内存占有量，便于迭代算法解方程组时程序的调用。

（2）随着频率的增加，电场的异常极值逐渐向深部移动，较高频段对异常体的反应较强，在实际应用中，尽可能选择一个合适的频率段；随着收发距的增加，异常逐渐减弱，异常等值线的密集带逐渐减稀疏，纵向分辨的能力变差，实际应用时要选择一个较小的收发距。

（3）模拟研究为地－井电磁法三维反演奠定了基础。

（4）频率域地－井电磁法响应特征规律复杂，本文只考虑了异常体电阻率的大小、埋深、异常体与收发位置关系对其异常产生的影响，模型的尺寸、形状以及各种组合异常体同样需要考虑；选取的场源及模型都是在二维情况下计算的，为了得到更好的模拟效果，需选择更适当的场源进行三维模拟提高模拟精度。

（5）在地井观测方式下，为了突出异常体的响应，减小总场对二次场的影响，采用的是利用背景场进行归一化的方法。在实际的工作中很难准确得到背景场的值。为了更有效地在总场中提取微弱的二次场异常是一个更重要的问题，需要更进一步深入的研究。

［1］杨曦，潘和平．井间电磁场数值模拟及成像技术［J］．物探与化探，2009，33（2）：140－147．

［2］何展翔．圈定油气藏边界的井地电法研究［D］．成都：成都理工大学，2006．

［3］王志刚，何展翔，魏文博，等．井地电法的准解析近似三维反演研究［J］．石油地球物理勘探，2007，42（2）：220－225．

［4］Augustin A M，Kennedy W D，Morrison H F，et al．A Theoretical Study of Surface to Borehole Electromagnetic Logging in Cased Holes［J］．Gephysics，1989，54（1）：90－99．

［5］Wilt M J，Alumbaugh D L，Morrison H F，et al．Croswwell Electromagnetic Tomography：System Design Considerations and Field Results［J］．Gephysics，1995，60（3）：871－885．

［6］魏宝君，张庚骥．地面－井孔电磁系统成像方法研究［J］．石油大学学报：自然科学版，1999，23（6）：24－29．

［7］李静和，何展翔．地井垂直电磁 Walkaway剖面法油藏开发三维模型电场响应特征［J］．石油地球物理勘探，2012，47（4）：653－666．

［8］周峰，潘和平，文国军，等．基于有限差分的井中激发极化三维正演［J］．电波科学学报，2010，25（4）：785－792．

［9］孟庆鑫，潘和平．地－井瞬变电磁响应特征数值模拟分析［J］．地球物理学报，2012，55（3）：1046－1053．

［10］孙向阳，聂在平，李爱勇，等．用高阶叠层矢量有限元法计算随钻测井的三维电磁响应［J］．电波科学学报，2009，24（2）：273－279．

［11］刘申芬，李天成，慕洪涛．三维井地电阻率有限元数值模拟及反演［J］．物探与化探，2009，33（1）：88－90．

［12］李琳，李丽娟，高长征，等．电介质半空间两耦合线天线的时域积分方程法［J］．电波科学学报，2008，23（3）：411－416．

［13］王若，王妙月，底青云．频率域线源大地电磁法有限元正演模拟［J］．地球物理学报，2006，49（6）：1858－1866．

［14］李杰．频率域可控源二维有限元正演数值模拟［D］．长沙：中南大学，2010．

［15］柳建新，蒋鹏飞，童孝忠，等．不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用［J］．中南大学学报：自然科学版，2009，40（2）：484－491．