基于ICCG方法的随钻方位电磁波测井响应模拟研究

谢关宝，杨震，赵文杰

（1．中石化石油工程技术研究院，北京100101；2．中国石油大学（北京），北京102249；3．中石化胜利油田博士后工作站，山东 东营257017）

0 引 言

传统随钻电磁波电阻率测井仪采用同轴发射－接收线圈，这种仪器结构和方法不能反映地层方位信息，在地质导向应用过程中存在很大局限性。新一代随钻电磁波电阻率测井仪装有倾斜（或水平）发射／接收线圈，可提供地层方位信息［1］。2005年斯伦贝谢公司推出第一代随钻方位电磁波电阻率测井仪PeriScope，2006年贝克休斯公司推出随钻方位电磁波电阻率测井仪APR，2007年哈里伯顿公司推出随钻方位电磁波电阻率测井仪 ADR［2－4］，其特点是采用复合线圈系、多种频率测量，提供多种探测深度的幅度比和相位差。本文以三线圈系为基础，模拟带有倾斜接收线圈的方位电磁波电阻率仪器的响应规律，为仪器研发和地质导向应用提供理论依据。

1 数学建模

1．1 数学物理模型

计算模型为单发双收线圈系，发射线圈T与仪器轴垂直（见图1），接收线圈相对于仪器轴存在一定夹角。假设地层坐标系为xyz，仪器轴相对于水平地层的倾角为α，方位角为β（相对于x轴），接收线圈磁矩与仪器轴线所在垂面夹角为γ。仪器的参考坐标系为x′y′z′，地层坐标系与仪器坐标系之间的磁矩转换关系为

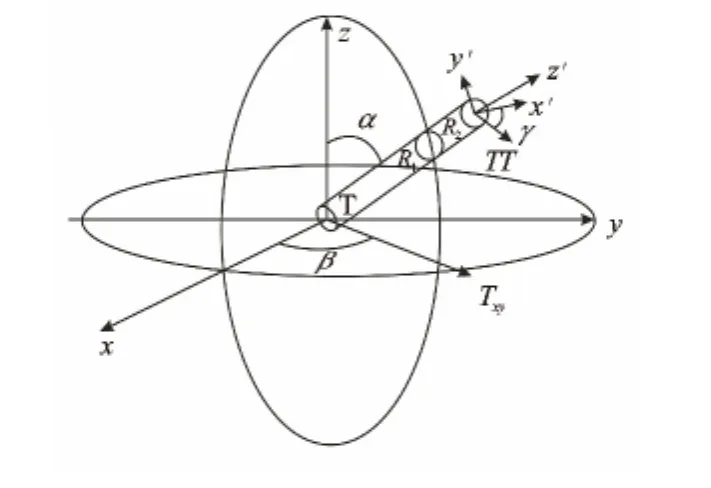
图1 三线圈系坐标示意图

电磁场数值模拟中的频率域麦克斯韦方程［5］可表示为

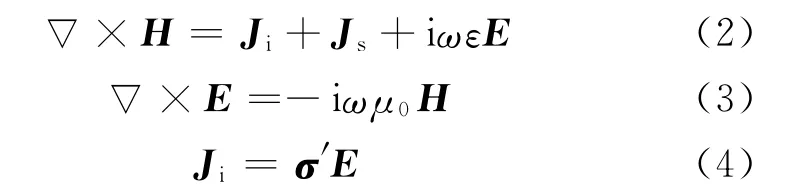
式中，H、E分别为磁场强度和电场强度；Ji为感应电流密度；Js为源电流密度；ω为角频率；μ0＝4π×10－7（H／m）；σ′为复电导率张量，σ′＝σ＋iωε；ε为介电常数。为了得到场源附近精确的电磁场分布，需要精细的网格划分，因此把式（2）中的总电场分解为背景场Eb和散射场E′，即

由式（2）至式（5）得

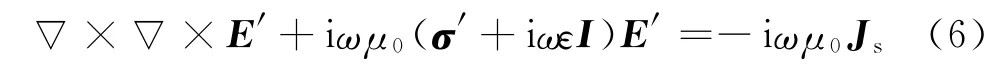
式中，Js＝［（σ′－σ′0I）＋iω（ε－ε0）I］E0；σ′0为背景电导率；ε和ε0分别为介电常数和背景介电常数，由于ε和ε0的数量级很小，故Js≈（σ′－σ′0I）E0。

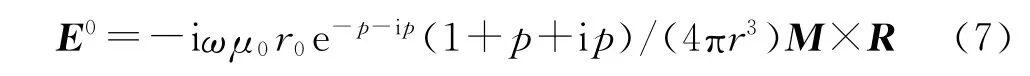
在直角坐标系中，对式（6）进行有限差分离散。离散时采用KANE S Yee提出的交错网格［6］（见图2）。在交错网格中，电场E在单元棱边上采样，磁场H在单元面中心采样。该方法的优点在于微分Maxwell方程组成的梯度、旋度、散度关系式对其差分模拟依然成立，从而保证了在无源区电流守恒，即

使用交错网格对微分方程进行有限差分离散不会产生赝解［7］。

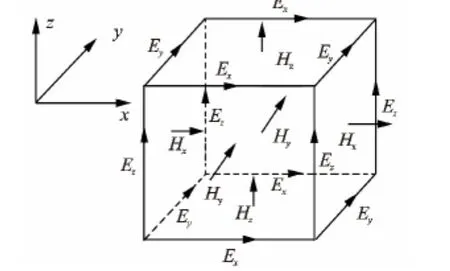
图2 交错网格示意图

考虑地层为有耗媒质，电磁波衰减较快，在数值模拟过程中须采用有限空间作为求解区域。在区域边界上，电场E满足Dirichlet边界条件0，其中∂Ω为求解区域Ω的边界。

散射电磁场可分解为

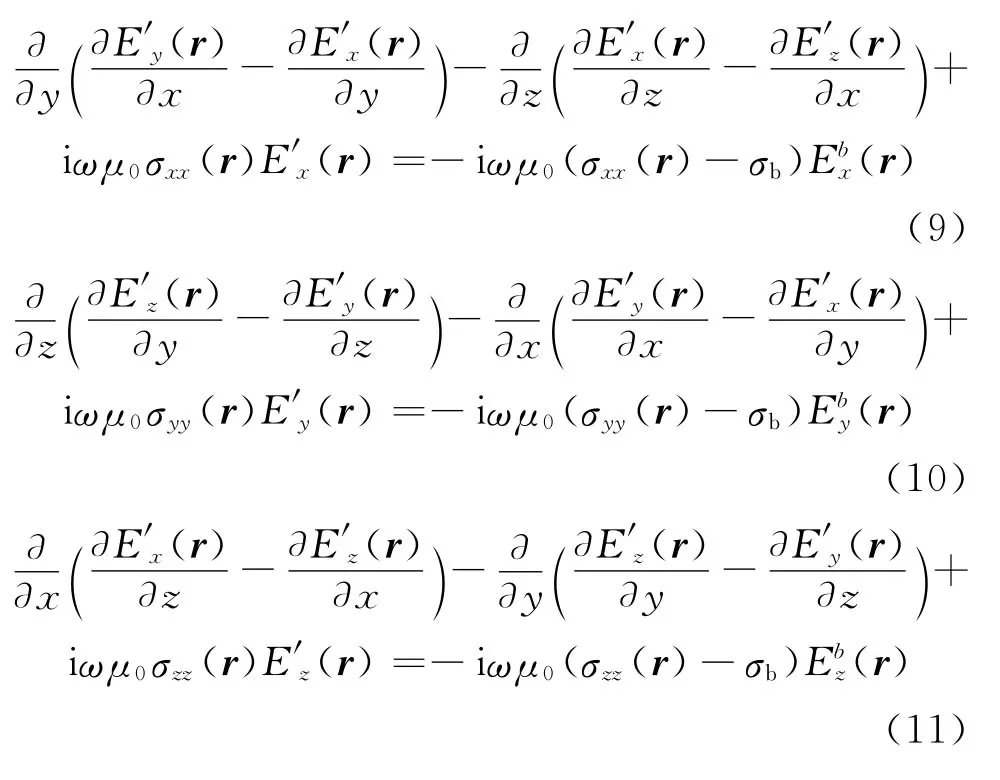
式中，σxx（r）、σyy（r）和σzz（r）分别为x、y和z方向的电导率；σb为背景电导率。

对每一个节点的x、y、z分量分别按式（9）至式（11）进行差分，所有节点形成等效方程组

式中，A为超大型正定对称稀疏复数矩阵，完全存储需较大内存，对方程进行差分计算发现，矩阵A每行最多只有13个非0元素（见图3），这是应用ICCG方法的基础。在安装矩阵A的过程中，只需安装内点，对于和Dirichlet边界相邻的内点，在其对应方程中，略去和边界点对应的项即可。建立地层模型在x、y、z方向上分别有Nx、Ny、Nz个节点，施加Dirichlet边界条件后，共有3NxNyNz－5（NxNy＋NyNz＋NxNz）＋8（Nx＋Ny＋Nz）－12个未知数，即形成3NxNyNz－5（NxNy＋NyNz＋NxNz）＋8（Nx＋Ny＋Nz）－12个方程。

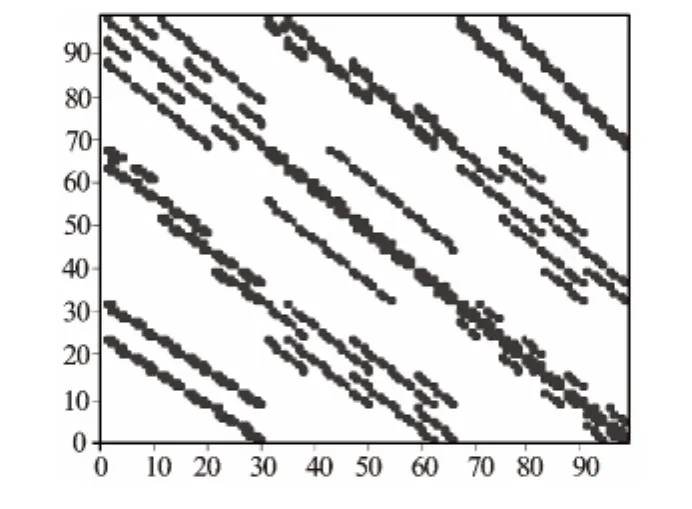
图3 稀疏矩阵非0元素分布

得到地层电磁场分布后，则可进一步得到2个接收线圈上的感应电动势VR1和VR2，则实际测井记录的幅度比和相位差为［8］

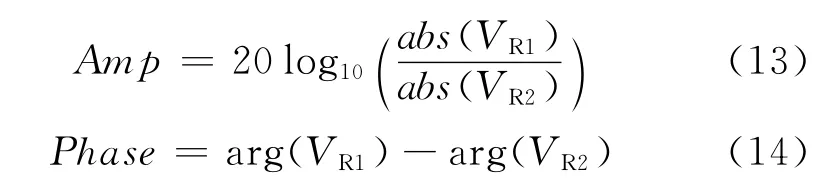
式中，arg表示取相位角。根据幅度衰减和相位差转换就可以得到随钻电磁波电阻率。

1．2 改进的ICCG算法

共轭梯度法理论上n步之内可以收敛，但一般情况下n次迭代难以得到满意精度的解，需要反复迭代，大大限制了共轭梯度的应用，需要引入预条件技术，预条件的思路是寻找A的一个近似分解

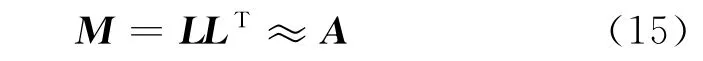
尽管ICCG方法实现了对称正定矩阵高效分解，但在计算过程中并不能保证不出现对角元为负或幅值很小的情况。当对角元为负时，会影响预处理矩阵的正定性，与矩阵A的近似程度也会下降；当对角元幅值很小时，必然引起舍入误差增大，从而影响分解质量和求解效率。本文采用张永杰［9］等提出的对角元修正方法提高ICCG方法的分解质量和求解效率。

令T为预处理矩阵M＝LLT第i行的1范数，即

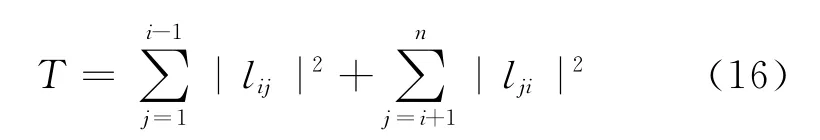
式中，lij、lji分别为下三角矩阵L中的元素。当分解过程中对角元dii＜T时，取dii＝T；对角元dii＞T时，不进行修正。

图4为分别用改进的ICCG和ICCG计算同一方程的收敛过程比较，很明显，改进的ICCG的残差随迭代次数的增加迅速下降，而普通ICCG方法中，残差的震荡性比较强，需迭代更多的次数［10］。

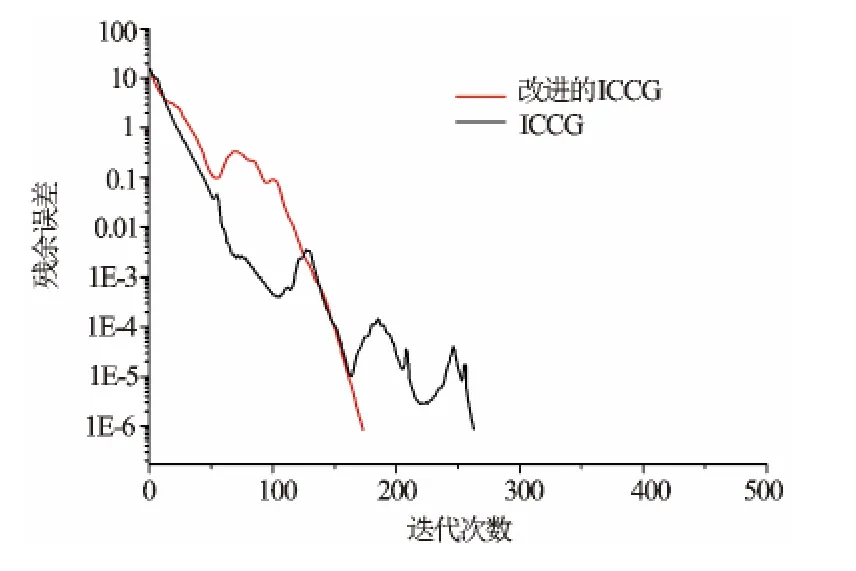
图4 改进的ICCG和ICCG收敛过程比较

2 数值模拟结果分析

计算模型中2个接收线圈与发射线圈之间的距离分别为0．6m和0．76m，仪器工作频率为2MHz，地层的相对介电系数εr＝10。地层模型为三层各向同性地层，电阻率分别为1、10Ω·m和1Ω·m，井眼于地层的相对倾角为80°（见图5），地层界面位置为z0＝1．5m，z1＝3．5m。图6、图7分别模拟了在钻进过程中，接收线圈处于不同方位角时的幅度比和相位差（接收线圈与仪器轴的夹角为45°）。该计算方法的正确性和准确性在以前发表的文章［11］中与一维解析解进行了对比，结果相吻合，证明了该计算方法准确可靠。

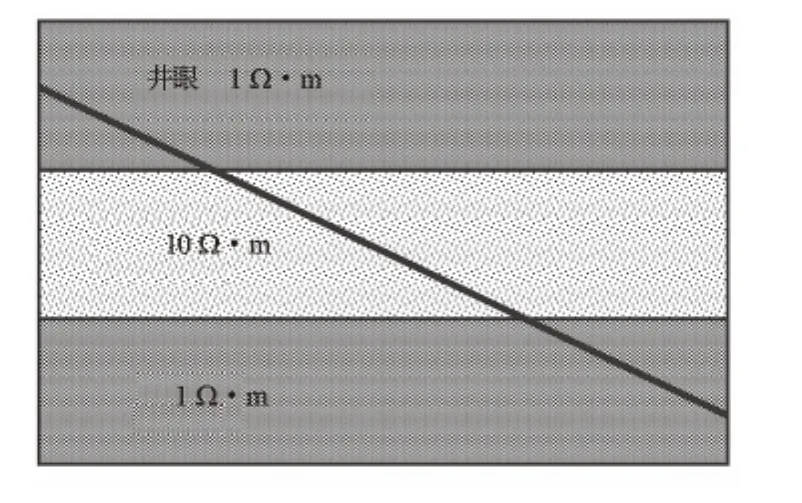
图5 井眼轨迹示意图

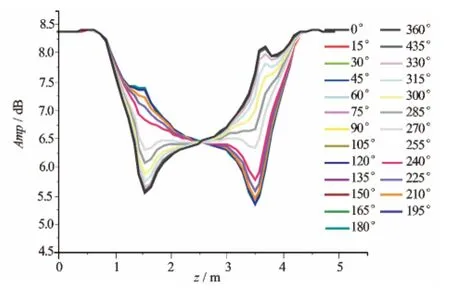
图6 方位电磁波电阻率仪器随接收线圈方位变化幅度比模拟结果（θR＝45°）

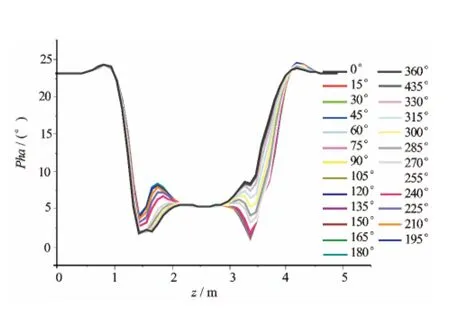
图7 方位电磁波电阻率仪器随接收线圈方位变化相位差模拟结果（θR＝45°）

通过模拟结果可以看出，当方位电磁波仪器以较大相对倾角（80°）穿过地层界面时，仪器响应同样出现极化角［12］，该极化角对地层界面同样有良好的识别作用。但与传统的电磁波电阻率仪器响应不同，极化角幅度和位置与接收线圈的方位有关系，正是这种关系的存在，采用该种结构的仪器可以实现对方位的识别。接收线圈在界面处的感应电动势随方位角γ周期性变化。这种响应的变化只是出现在地层界面处，而离开地层界面一定距离后，仪器的响应不再随接收线圈方位角的变化而变化，这就使仪器在能够区别地层方位进行精确地质导向的时候同时具备了地层评价的能力。

在仪器旋转过程中，当接收线圈的磁矩与地层界面垂直时（γ＝0°和γ＝180°），极化角幅度最大，此时对地层定位能力最强［12］。当接收线圈磁矩与地层界面平行时（γ＝90°和γ＝270°），仪器响应与常规电磁波电阻率仪器相同。

图8、图9为模拟接收线圈与仪器轴夹角为60°的情况下的仪器响应。随着接收线圈倾斜角增加，幅度比和相位差的极化角在地层界面处幅度有所增加，变化更加明显。这是由于随着相对倾斜角的增加，在地层界面附近会导致磁场的ZX分量增加，这对于定向应该是有利的；但随着倾斜角的增加，接收线圈处的感应电动势中能反映地层电阻率的电磁场ZZ分量比重降低，导致幅度比和相位差的误差增大，不利于地层评价。因此目前国外公司商业应用的方位电磁波仪器普遍选择θR＝45°的方案。

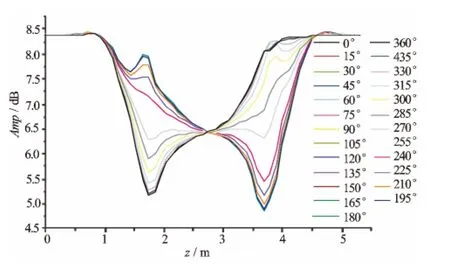
图8 方位电磁波电阻率仪器随接收线圈方位变化幅度比模拟结果（θR＝60°）

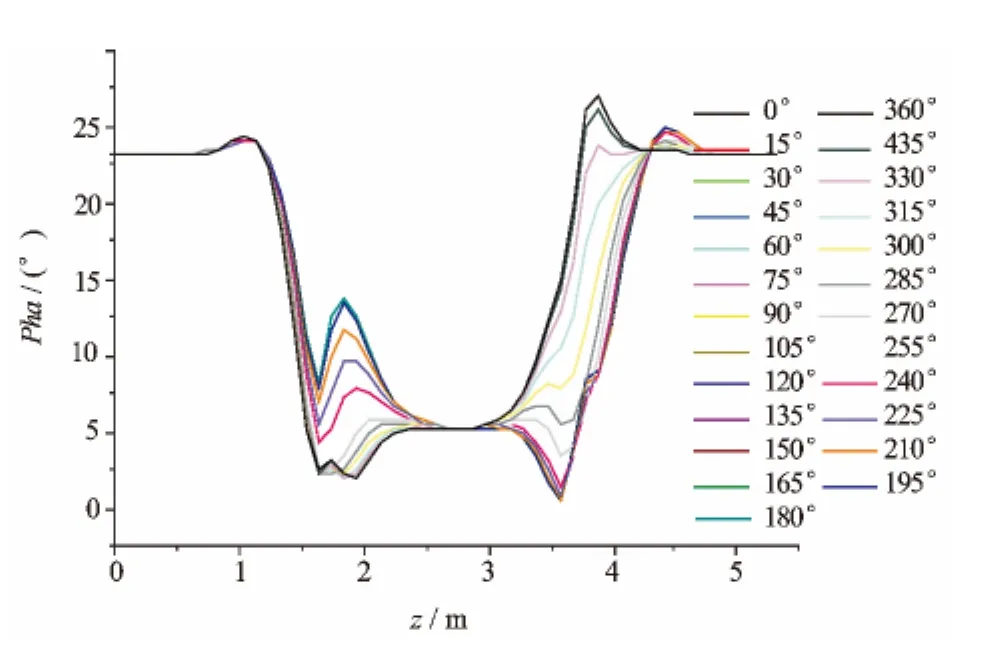
图9 方位电磁波电阻率仪器随接收线圈方位变化相位差模拟结果（θR＝60°）

在图10地层模型中，仪器在钻进过程中可能会遇到10Ω·m的目的层，分别位于仪器的上方或下方，常规随钻电磁波电阻率仪器响应是相同的，反映不出地层模型的差异。但在实际钻井过程中，如果遇到类似地质情况，需要调整钻头钻进方向，以使钻头进入可能含油的高电阻率地层，常规随钻电磁波电阻率仪器就无能为力了，但通过方位电磁波电阻率仪器的响应（见图11），可以明显区别判断2种地层模型，实现地质导向。

图10 地层模型示意图

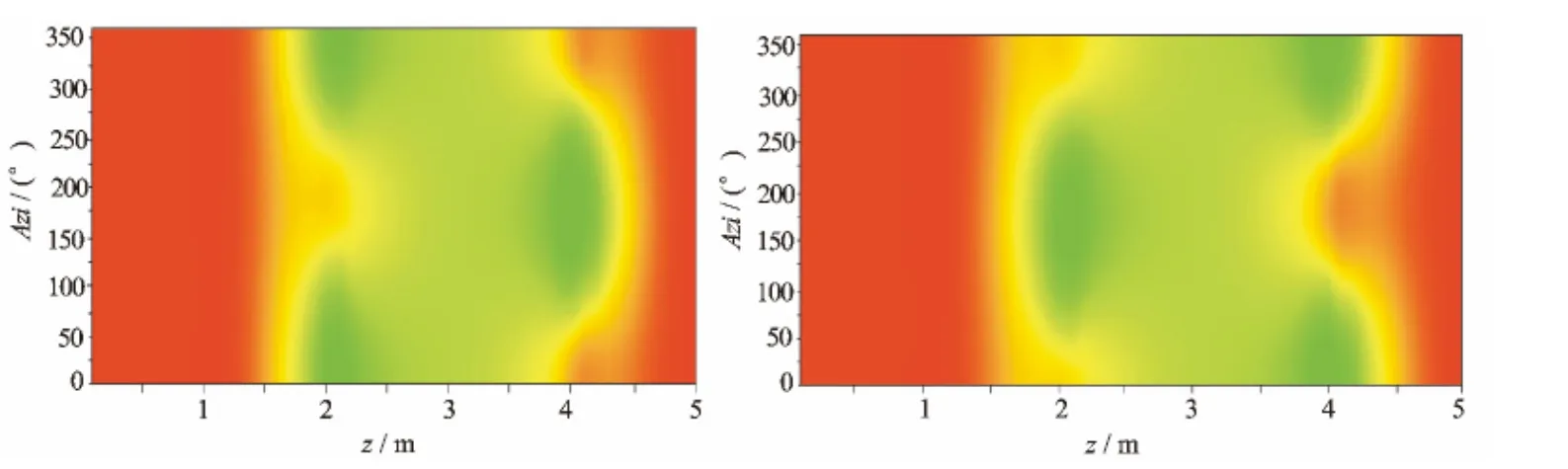
图11 方位电磁波电阻率响应模拟结果

3 结 论

（1）随钻方位电磁波电阻率测井仪在钻进过程中，仪器响应会出现极化角，该现象只出现在地层界面处，且在离开界面时不随接收线圈方位角的变化而变化，从而结合方位信息，可以指导钻头钻进方向，实现地质导向。

（2）在仪器旋转过程中当接收线圈的磁矩与地层界面垂直时（γ＝0°和γ＝180°），极化角的幅度最大，此时对地层的定位能力最强；当接收线圈的磁矩与地层界面平行时（γ＝90°和γ＝270°），仪器的响应与常规的电磁波电阻率仪器相同。

（3）接收线圈与仪器轴的夹角影响极化角的幅度，夹角太小会导致界面指示作用减弱，夹角太大则会影响仪器地层评价的精度。

［1］Prensky S．Recent Advances in LWD／MWD and Formation Evaluation［J］．World Oil，2006，227（3）：69－74．

［2］Li Q，Omeragic D，Chou L，et al．New Directional Electromagnetic Tool for Proactive Geosteering and Accurate Formation Evaluation While Drilling［C］∥SPWLA 46th Annual Logging Symposium，Paper UU，June 2005．

［3］Bittar M S，Klein J，Beste R，et al．A New Azimuthal Deep Reading Resistivity Tool for Geosteering and Advanced Formation Evaluation［C］∥SPE Annual Technical Conference and Exhibition Transactions，SPE Pa－per 109971，November 2007．

［4］Zhang Zhiyi，Christophe Gonguet，Vinit Rajan，et al．Diectional LWD Resistivity Tools and Their Business Impacts［C］∥ SPWLA 49th Annual Logging Symposium，Paper FFFF，May 2008．

［5］梁灿彬，秦光戎，梁竹健．电磁学［M］．北京：高等教育出版社，1985．

［6］KANE S Yee．Numerical Ssolution of Initial Boundary Problem Involving Maxwell’s Equation in Isotropic Media［C］∥IEEE Transactions Antennas Propagation，1966，14（3）：302－307．

［7］杨震，范宜仁，文艺，等．三维频率域随钻电磁波测井数值模拟［J］．地球物理学进展，2009，24（5）：1833－1838．

［8］杨锦舟，魏宝君，林楠．倾斜线圈随钻电磁波电阻率测量仪器基本原理及其在地质导向中的应用［J］．中国石油大学学报：自然科学版，2009，33（1）：44－49．

［9］张永杰，孙秦，李江海．大型稀疏线性方程组的改进ICCG方法［J］．计算物理，2007，24（5）：581－584．

［10］杨震．非均匀复杂地层随钻电磁波测井响应研究［D］．东营：中国石油大学（华东），2009．

［11］杨震，刘庆成，岳步江．随钻电磁波测井资料中“极化角”的形成机理及影响因素分析［J］．测井技术，2010，34（3）：210－214．

［12］魏宝君，田坤，张旭．定向电磁波传播随钻测量基本理论及其在地层界面探测中的应用［J］．地球物理学报，2010，53（10）：2507－2515．