Monte Carlo Simulation of Ti-6Al-4V Grain Growth during Fast Heat Treatment

Amir Reza Ansari Dezfoli,Weng-Sing Hwang,2

Monte Carlo Simulation of Ti-6Al-4V Grain Growth during Fast Heat Treatment

Amir Reza Ansari Dezfoli1,Weng-Sing Hwang1,2

Investigations of the microstructural evolution of Titanium(Ti)alloys during high temperature processes and heat treatment are attracting more attention due to wide variety of applications for such alloys.In most of these processes the Titanium alloys are subjected to fast heating or cooling rates.In this paper,Monte Carlo simulation is used to simulate the grain growth kinetics of Ti-6Al-4V alloy during fast heat treatment.Here,Monte Carlo simulation of grain growth is based on the Q-state Potts model.Our model is calibrated using the parabolic grain growth law,where the empirical constants are taken from the literature.The simulation results are compared with the experimental data,and this comparison shows good agreement between the two.

Ti-6Al-4V;Grain growth;Monte Carlo simulation;Q-state Potts model;Fast heat treatment.

1 Introduction

Titanium undergoes a phase transformation from α-phase(hexagonal close-pack)to β-phase(body-centered cubic)at a temperature 883°C[Donachie(2000)].Adding other element to pure Titanium leads to stabilization of the α or β phase.For example,Al is known as an α-stabilizer element while V is considered as a β-stabilizer[Blackburn(1967);Kattner,Lin,and Chang(1992);Zhang,Cao,and Guo(2014)].Ti-6Al-4V is one of the most important Titanium alloys,and contains a mixture of Ti,Al and V with the chemical formula Ti-6.04Al-4.03V-0.12Fe-0.09O-0.03C-0.009N[Ahmed and Rack(1998)].Ti-6Al-4V has a number of superior properties,such as high corrosion resistivity,high strength,good formability and low density.Due to these properties Ti-6Al-4V is used in applications such as aircraft turbine engine components,aircraft structural components,aerospace fas-teners,high-performance automotive parts,marine applications,medical devices,and sports equipment[PalDey and Deevi(2003);Wang(1996)].

In order to enhance the mechanical properties of Ti-6Al-4V products,post-production heat treatment is necessary[Vrancken,Thijs,Kruth,and Van Humbeeck(2012)].Experimental investigations proved that at room temperature the microstructure of Ti-6Al-4V contains elongated α grains surrounded by small amount of β-phase[Elmer,Palmer,Babu,and Specht(2005);Vrancken,Thijs,Kruth,and Van Humbeeck(2012)].If Ti-6Al-4V is heated above 995°C,a fully homogeneous β-phase microstructure is formed[Vrancken,Thijs,Kruth,and Van Humbeeck(2012);Weiss and Semiatin(1998)].The heat treatment of Ti-6Al-4V can be classified based on the heat treatment temperature compared to the β-transus temperature.The heat treatment can be proceed at subtransus temperature(a temperature less than β-transus,995°C)or super-transus temperature(a temperature higher than β-transus,995°C).β-phase grain growth is obviously predominant during heat treatment in the supertransus condition.Based on the required time,the heat treatment can be also divided into two major categories:long-time(furnace,t＞100s)and short-time(salt pot and induction,0＜t＜100s)methods[Ivasishin,Shevchenko,and Semiatin(2002)].Therefore,if the duration of Ti-6Al-4V heat treatment is less than 100s and the temperature more than 995°C,the grain growth is considered as short-time β grain growth.

The β-grain size,which is the average grain size after heat treatment,is an important factor in determining the final mechanical properties of the Titanium alloys produced using short-time heat treatment[Ivasishin,Shevchenko,and Semiatin(2002);Ivasishin(2001)].Some experimental efforts have been made in order to predict β grain size during short time heat treatments[Ivasishin,Shevchenko,and Semiatin(2002);Semiatin,Soper,and Sukonnik(1996)].In this study,we use the Monte Carlo method to investigate the β-grain growth of Ti-6Al-4V in short time heat treatment,as this method has been widely used to simulate grain growth in isothermal and non-isothermal conditions[Gao and Thompson(1996);Mishra and DebRoy(2004a,b);Yang,Sista,Elmer,and DebRoy(2000)].In addition the Monte Carlo method is used to simulate different processes and phenomena in engineering in micro and micro scales[Bhuvaraghan,Srinivasan,Maffeo,and Prakash(2010);Chen,Ma,and Gao(2012);Hernández-Rivera,Tikare,Wang,and Wang(2013);Huang,Tsai,Liu,Jeng,and Yang(2009);Liu,Liu,and Liu(2013)].At the first step,the temperature history is calculated using Lumped theory.In the next step,the relation between real time and Monte Carlo steps is developed using the experimental results obtained by Semiatin,Soper,and Sukonnik(1996).Using these two steps,the grain structure of Ti-6Al-4V alloy is simulated.The comparison made in the final step in this paper proves that good correspondence is obtained between the simulation results and the experimental results available in the literature.

2 Simulation Procedure

2.1 Heat Transfer Model

A 25×38×1.3mm Ti-6Al-4V system is considered.In order to make a comparison between theoretical and experiment data,the dimensions of the system are chosen to be the same as in Semiatin,Soper and Sukonnik(1996)’s experimental study.Initially,the temperature of the system is considered at room temperature,T0(298K).The system is then heated up using a hot liquid bath with the constant temperature,T∞.

The temperature uniformity of the system is checked by Lumped theory[Cengel and Hernán Pérez(2004);Incropera(2011)].In this theory,the Biot Number,Bi,is used to check the ratio between heat transfer resistance inside and on the surface of the system.The temperature in the system can be considered uniform for systems with a Biot number smaller than 1.The Biot number is expressed as[Incropera(2011)]:

The characteristic length,lc,is defined as the ratio between the volume of the body and the surface area of the system,such as:

If the criteria for Lumped theory are accepted then the heat transfer into the system during the time step,dt,can increase the energy of the system equal to ρVcpdT/dt[Incropera(2011)].Therefore:

Simplifying the above equation,considering(T(t=0)=T0andand using integration,the solution of Equation(3)can then be written as;

2.2 Grain Growth

In order to simulate the grain structure during heat treatment,the Q-state Potts model is used,and this is a general case of the Monte-Carlo method for grain growth simulation,the details of which can found in the literature[Anderson,Srolovitz,Grest,and Sahni(1984);Saito and Enomoto(1992)].In this method,the micro structure is mapped onto discrete cells.Each cell in the simulation can have one of the 1 to Q states,which represent different crystallographic directions for grain growth.During the simulation it is necessary to consider a large number of grain orientations,Q,otherwise grains with the same orientation impinge infrequently.For Q＞30,the final results are essentially independent of Q[Anderson,Srolovitz,Grest,and Sahni(1984)].

In a Monte-Carlo simulation the energy of the system is described as[Anderson,Srolovitz,Grest,and Sahni(1984);Saito and Enomoto(1992)]:

N is the number of cells and z indicates the number of nearest neighbors to cell number i.The Kronecker delta function is defined as δ(qi,qj)=1 if qi=qj,and 0 otherwise.

Generally,the simulation algorithm of grain growth is based on the tendency of lattice points to achieve minimum energy.The basic Monte-Carlo algorithm can be brie fly explained as follows:

•Randomly select a cell.

•Assign a new state,q,for the cell.

•Calculate the energy difference before and after the change.

•If the energy of the system is decreased,the random change is kept.

•If the energy is increased,the random change is a?llowed? to remain with a probability equal to the Boltzmann factor,

Each Monte-Carlo time step(MCS)requires N attempted state changes,where N is the number of cells.The most important challenge in the Monte Carlo method is finding a relation between real time and MCS.The simulated grain growth kinetics can be defined by the following equation[Gao and Thompson(1996)]:

L is the average grain size,dl is the cell length in Monte Carlo space,and K1and n1are model constants.On the other hand,most of the grain growth phenomena in materials can be described by the following parabolic equation[Gao and Thompson(1996)]:

Where L is the average grain size,t is the real time and L0is the initial grain size.Gao and Thompson used equations(6)and(7)and proposed the following equation in order to set a relation between the MCS and real time during grain growth[Gao and Thompson(1996)]:

Two parameters in Equation 6,K1and n1,should be found before setting a relation between MCS and real time.Taking the logarithm of both sides of Equation 6 gives:

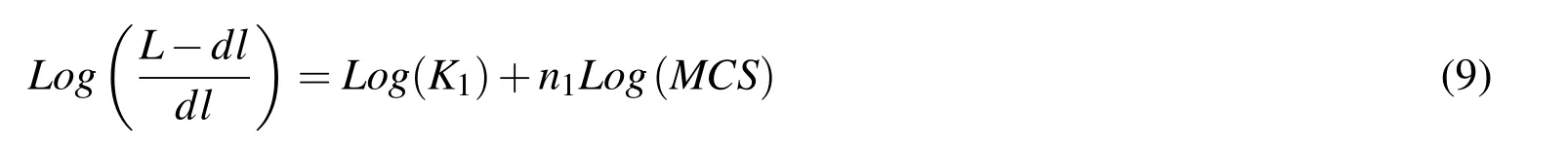
3 Results and discussion

The simulation set-up is exactly the same as that used in the experimental study carried by Semiatin,Soper and Sukonnik(1996).A Ti-6Al-4V sheet with dimensions of 25×38×1.3 mm is considered.This sample is heated in a liquid salt-pot at temperatures of 1032°C and 1088°C.In Semiatin study the samples were immediately water quenched to avoid grain changes during cooling.In this work the change in grain structure is also neglected during the cooling time.All the physical properties of the material used in this study are listed in Table 1.

Figure 1:Monte Carlo results.(a)G?rain s?ize versus MCS for Q=30 and T=1563 K.(b)Fitting graph for Plot ofVs.Log(MCS).

Table 1:Data used for the calculation of the grain growth kinetics of Ti-6Al-4V.

The convective heat transfer coefficient is considered equal to 585 j/sm2K[Semiatin,Soper,and Sukonnik(1996)].In this condition the Biot number is 0.01,which is very small,and thus the criterion for Lumped theory is met.The temperature history as a function of time during the heat treatment is shown in Figure 2.

The relation between MCS with respect to real time and temperature is demonstrated in Figure 3.Equation 8 is used in order to calculate the corresponding MCS for each time.In reality,the experimental results show that in the initial sample both α -and β -phases are available.During the heating up process,the α -phase starts to convert to the β -phase.B-phase dissolution is then completed at the β-transus temperature.The time required for this in our case is almost 7 seconds,which is named the sub-transus period.An earlier experimental investigation showed that the grain growth during the sub-transus period is very small[Semiatin,Soper,and Sukonnik(1996)].Figure 3 also reveals that the MCS before the β-transus temperature is reached is almost zero,which means there is no grain growth below the β-transus temperature.

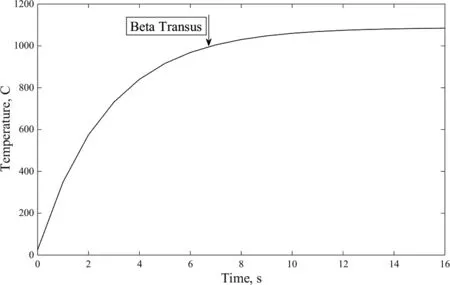
Figure 2:Temperature history in the sheet using the Lumped model.

Figure 3:The relationship of the MCS with real time and temperature during the simulation.(a)Real time Vs.MCS,(b)Temperature Vs.MCS.

In order to calculate grain size,a(200×200)grid system is considered corresponding to a domain size of(200×40µm)×(200×40µm)=(8.0×8.0)mm.The grain size of the system is calculated during 100s heat treatment.Due to the statistical properties of the Monte Carlo method,for each case more than 10 repetitions were conducted and the average values are reported.The grain structures for different times are shown in Figure 4.The simulated morphology of the system shows that the grain size increases as a function of time during heating up.This occurs due to a reduction in the total energy of the system,which is achieved by reducing the total area of the grain boundary.This phenomena is consisted with the Monte Carlo procedure,in which any change is kept if leads to a more stable thermodynamic state.

Figure 5 shows a comparison of the grain sizes in different experimental studies,empirical equations and our Monte Carlo simulation.The empirical equations are based on Equation 7.The coefficients from an earlier study[Semiatin,Soper,and Sukonnik(1994)]are n=2.0,Q=251 kJ/mol and k=2.02,while in the current study they are n=2,Q=312 kJ/mol and k=1110[Semiatin,Soper,and Sukonnik(1996)].

Figure 4:Grain structure by the Monte Carlo method after(a)50 s,and(b)100 s.

Figure 5:Predicted grain size Vs.time based on the Monte Carlo method(this study),experimental data[Semiatin,Soper,and Sukonnik(1994,1996)]and empirical parabolic grain-growth law equation[Semiatin,Soper,and Sukonnik(1994,1996)]at 1088°C.

This comparison also proves the good prediction of grain size made by the Monte Carlo method.A large difference is indicated in Figure 5 between the results in Semiatin(1994)on the one hand,and our Monte Carlo results and those in Semiatin(1996)on the other.Mathematically,a much smaller k in the earlier case leads to the prediction of slow grain growth during the heat treatment.Physically,this difference is due to the presence of molybdenum in the samples used by Semiatin(1994),where the diffusivity of molybdenum in beta Ti is slow as found by[Zwicker(1974)].

All procedures were repeated for the liquid salt-pot at a temperature of 1032°C,and the results are shown in Figure 6.The comparison again shows good agreement between the experimental and simulation results.

Figure 6:Predicted grain size Vs.time based on the Monte Carlo method(this study),experimental data[Semiatin,Soper,and Sukonnik(1994,1996)]and the empirical parabolic grain-growth law equation[Semiatin,Soper,and Sukonnik(1994,1996)]at 1032°C.

4 Conclusion

A Monte Carlo simulation based on the Q-states Potts model is applied in this work to study the kinetics of beta grain growth during short-time supertransus heat treatment of Ti-6Al4V.The relations between the Monte Carlo simulation iterations and real time-temperature kinetics are developed based on the parabolic grain growth law.The results of this simulation correlate well with the experimental results.This study thus shows that the Monte Carlo simulation of grain growth methodology can be applied to simulate the Ti-6Al-4V microstructure during manufacturing processes that involve fast heat treatment.

Ahmed,T.;Rack,H.(1998):Phase transformations during cooling in α +β titanium alloys.Materials Science and Engineering:A,vol.243,pp.206–211.

Anderson,M.;Srolovitz,D.;Grest,G.;Sahni,P.(1984):Computer simulation of grain growth—I.Kinetics.Acta metallurgica,vol.32,pp.783–791.

Bhuvaraghan,B.;Srinivasan,S.M.;Maffeo,B.;Prakash,O.(2010):Analytical solution for single and multiple impacts with strain-rate effects for shot peening.Computer Modeling in Engineering and Sciences(CMES),vol.57,pp.137.

Blackburn,M.(1967):The ordering transformation in titanium-aluminum alloys containing up to 25 at.pct aluminum(Ti-Al alloys ordering transformation studied by electron microscopy and electron and X-ray diffraction,showing existence of three phase fields).AIME,Transactions,vol.239,pp.1200–1208.

Brook,G.(1998).Smithells light metals handbook.Butterworth-Heinemann.

Cengel,Y.A.;Hernán Pérez,J.(2004):Heat transfer:a practical approach.Transferencia de calor.

Chen,T.;Ma,H.;Gao,W.(2012):Comprehensive investigation into the accuracy and applicability of Monte Carlo simulations in stochastic structural analysis.Computer Modeling in Engineering&Sciences(CMES),vol.87,pp.239–269.

Donachie,M.J.(2000).Titanium:a technical guide.ASM international.

Elmer,J.;Palmer,T.;Babu,S.;Specht,E.(2005):Low temperature relaxation of residual stress in Ti-6Al-4V.Scripta Materialia,vol.52,pp.1051–1056.

Gao,J.;Thompson,R.(1996):Real time-temperature models for Monte Carlo simulations of normal grain growth.Acta Materialia,vol.44,pp.4565–4570.

Hernández-Rivera,E.;Tikare,V.;Wang,L.;Wang,H.(2013):Numerical simulation of radiation-induced chemical segregation and phase transformation in a binary system.CMC:Computers,Materials&Continua,vol.38,pp.91–103.

Huang,M.-J.;Tsai,T.-C.;Liu,L.-C.;Jeng,M.-s.;Yang,C.-C.(2009):A fast Monte-Carlo solver for phonon transport in nanostructured semiconductors.Computer Modeling in Engineering and Sciences(CMES),vol.42,pp.107.

Incropera,F.P.(2011).Fundamentals of heat and mass transfer.John Wiley&Sons.

Ivasishin,O.;Shevchenko,S.;Semiatin,S.(2002):Effect of crystallographic texture on the isothermal beta grain-growth kinetics of Ti-6Al-4V.Materials Science and Engineering:A,vol.332,pp.343–350.

Ivasishin,O.M.(2001):Mechanism of beta-grain growth in alpha/beta titanium alloys during continuous,Rapid Heating.DTIC Document.

Kattner,U.;Lin,J.-C.;Chang,Y.(1992):Thermodynamic assessment and calculation of the Ti-Al system.Metallurgical Transactions A,vol.23,pp.2081–2090.

Liu,X.;Liu,Y.;Liu,H.(2013):Magnetorheological fluids particles simulation through integration of Monte Carlo method and GPU accelerated technology.CMES:Computer Modeling in Engineering&Sciences,vol.91,pp.65–80.

Mishra,S.;DebRoy,T.(2004a):Grain topology in Ti-6Al-4V welds—Monte Carlo simulation and experiments.Journal of Physics D:Applied Physics,vol.37,pp.2191.

Mishra,S.;DebRoy,T.(2004b):Measurements and Monte Carlo simulation of grain growth in the heat-affected zone of Ti-6Al-4V welds.Acta Materialia,vol.52,pp.1183–1192.

PalDey,S.;Deevi,S.(2003):Single layer and multilayer wear resistant coatings of(Ti,Al)N:a review.Materials Science and Engineering:A,vol.342,pp.58–79.

Saito,Y.;Enomoto,M.(1992):Monte Carlo simulation of grain growth.ISIJ international,vol.32,pp.267–274.

Semiatin,S.;Soper,J.;Sukonnik,I.(1994):Grain growth in a conventional titanium alloy during rapid,continuous heat treatment.Scripta metallurgica et materialia,vol.30,pp.951–955.

Semiatin,S.;Soper,J.;Sukonnik,I.(1996):Short-time beta grain growth kinetics for a conventional titanium alloy.Acta materialia,vol.44,pp.1979–1986.

Tian,J.;Han,X.;Long,S.;Xie,G.(2009):An analysis of the heat conduction problem for plates with the functionally graded material using the hybrid numerical method.Computers,Materials&Continua(CMC),vol.10,pp.229.

Vrancken,B.;Thijs,L.;Kruth,J.-P.;Van Humbeeck,J.(2012):Heat treatment of Ti6Al4V produced by Selective Laser Melting:Microstructure and mechanical properties.Journal of Alloys and Compounds,vol.541,pp.177–185.

Wang,K.(1996):The use of titanium for medical applications in the USA.Materials Science and Engineering:A,vol.213,pp.134–137.

Weiss,I.;Semiatin,S.(1998):Thermomechanical processing of beta titanium alloys—an overview.Materials Science and Engineering:A,vol.243,pp.46–65.

Welsch,G.;Boyer,R.;Collings,E.(1993).Materials properties handbook:titanium alloys.ASM international.

Yang,Z.;Sista,S.;Elmer,J.;DebRoy,T.(2000):Three dimensional Monte Carlo simulation of grain growth during GTA welding of titanium.Acta Materialia,vol.48,pp.4813–4825.

Zhang,M.-K.;Cao,B.-Y.;Guo,Y.-C.(2014):Numerical studies on damping of thermal waves.International Journal of Thermal Sciences,vol.84,pp.9–20.

Zwicker,U.(1974):Titan und titanlegierungen.

1Department of Materials Science and Engineering,National Cheng Kung University,University Road,Tainan 701,Taiwan

2Corresponding author.E-mail:wshwang@mail.ncku.edu.tw