New Spectral Solutions of Multi-Term Fractional-Order Initial Value Problems With Error Analysis

W.M.Abd-Elhameedand Y.H.Youssri

New Spectral Solutions of Multi-Term Fractional-Order Initial Value Problems With Error Analysis

W.M.Abd-Elhameed1，2and Y.H.Youssri2

In this paper,a new spectral algorithm for solving linear and nonlinear fractional-order initial value problems is established.The key idea for obtaining the suggested spectral numerical solutions for these equations is actually based on utilizing the ultraspherical wavelets along with applying the collocation method to reduce the fractional differential equation with its initial conditions into a system of linear or nonlinear algebraic equations in the unknown expansion coefficients.The convergence and error analysis of the suggested ultraspherical wavelets expansion are carefully discussed.For the sake of testing the proposed algorithm,some numerical examples are considered.The numerical results indicate that the resulting approximate solutions are close to the analytical solutions and they are more accurate than those obtained by some other existing techniques in literature.

Wavelets,ultraspherical polynomials,collocation method,fractionalorder differential equations

1 Introduction

Fractional calculus is an extension of derivatives and integrals to non-integer orders and has been widely used to model scientific and engineering problems.Fractionalorder differential equations have prominent roles in various disciplines.Due to their great importance,they have been investigated by a large number of authors from both theoretical and practical points of view(see,for example,[Diethelm(2010);Brunner,Pedas,and Vainikko(2001);Kilbas,Srivastava,and Trujillo(2006);Podlubny(1998);Kilbas,Marichev,and Samko(1993);Wang,Liu,Chen,Liu,and Liu(2015)]).It is well-known that many physical phenomena in acoustics,damping laws electroanalytical chemistry,neuron modeling,diffusion processing and material sciences(see for example,[Al-Mdallal,Syam,and Anwar(2010);Çenesiz,Keskin,and Kurnaz(2010);Daftardar-Gejji and Jafari(2005)])are described by fractional-order differential equations.Various algorithms are developed for handling different kinds of fractional differential equations.Some of these methods are,Adomian decomposition method[Momani(2007);Jafari and Seif i(2009)],variational iteration method[Sweilam,Khader,and Al-Bar(2007);Das(2009)]and fractional differential transform method[Arikoglu and Ozkol(2009);Erturk,Momani,and Odibat(2008)].

Spectral methods have important roles in many fields of applied science.The main characteristic of spectral methods is that the approximate solutions of differential equations are expressed in terms of truncated series of various orthogonal polynomials.There are three popular techniques for spectral methods,they are the collocation,tau and Galerkin methods(see,for instance[Abd-Elhameed,Doha,and Youssri(2013a,b);Abd-Elhameed(2014);Elgohary,Dong,Junkins,and Atluri(2014);Costabile and Napoli(2015);Abd-Elhameed(2015)]).

The subject of wavelets has recently drawn a great deal of attention from mathematical scientists in various disciplines.Wavelets have been used for solving ordinary and fractional differential equations.For example,a huge number of articles employ Legendre and Chebyshev wavelets for treating ordinary differential equations as well as fractional differential equations(see,for instance[Zhu and Fan(2012);Sadek,Abualrub,and Abukhaled(2007)]).In this paper,we aim to employ ultraspherical wavelets in handling fractional differential equations.A motivation for constructing and employing ultraspherical wavelets is that the Chebyshev and Legendre wavelets can be deduced as special cases of the ultraspherical wavelets.The ultraspherical polynomials have received considerable attention in recent decades,from both theoretical and practical points of view(see,for example[Elgindy and Smith-Miles(2013a)]).Some authors are interested in employing these polynomials for solving various kinds of differential equations.In this respect,Elgindy and Smith-Miles in[Elgindy and Smith-Miles(2013b)],treated boundary value problems,integral,and integro-differential equations using ultraspherical integration matrices.Moreover,Doha and Abd-Elhameed employed ultraspherical polynomials for solving one and two dimensional second-order differential equations in[Doha and Abd-Elhameed(2002)].In addition,the same authors in[Doha and Abd-Elhameed(2005)]developed some accurate spectral solutions for treating the parabolic and elliptic partial differential equations based on the ultraspherical tau method.

The main aim of this article is twofold:

•Deriving the ultraspherical wavelets operational matrix of the fractional integration.

•Analyzing efficient spectral wavelets algorithm for treating fractional-order differential equations via ultraspherical wavelets operational matrices of the fractional integration.

The contents of the paper are arranged as follows.Section 2 is devoted to presenting mathematical preliminaries containing some basic definitions in the fractional calculus theory which are required for establishing our results.Also,some relevant properties of ultraspherical polynomials and their shifted ones are presented and the ultraspherical wavelets are constructed.In Section 3,we investigate in detail the convergence and error analysis of the suggested ultraspherical wavelets expansion.In Section 4,the ultraspherical wavelets operational matrix of the fractional integration is derived.In Section 5,we present and implement an algorithm for solving multi-term fractional-order initial value problems based on employing the constructed ultraspherical wavelets operational matrix.In Section 6,some numerical examples are given to ensure the efficiency,simplicity and applicability of the suggested algorithm.Finally,conclusions are reported in Section 7.

2 Preliminaries

2.1 Some definitions and properties of fractional calculus

In this section,we present some notations,definitions and preliminary facts of the fractional calculus theory which will be useful throughout this article.

Definition 1.The Riemann-Liouville fractional integral operatorIαof order α on the usual Lebesgue spaceL1[0，1]is defined as

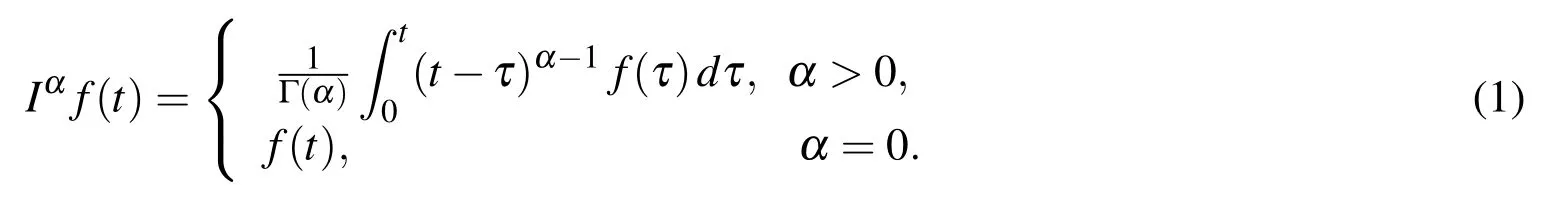
The operatorIαhas the following properties:

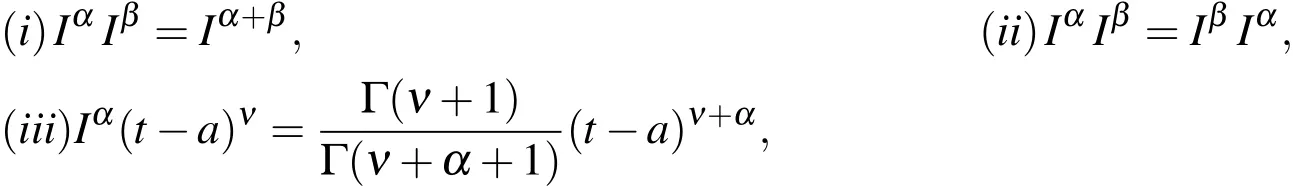
wheref∈L1[0，1]，α，β ≥ 0，and ν ＞ -1.

Definition 2.The Riemann-Liouville fractional derivative of order α＞0 is defined by

Definition 3.The Caputo definition of fractional differential operator is given by

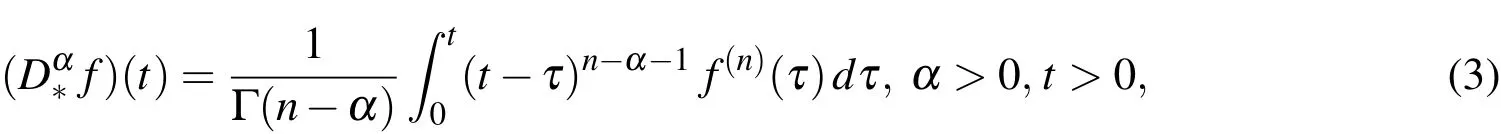
wheren-1≤α ＜n，n∈N.

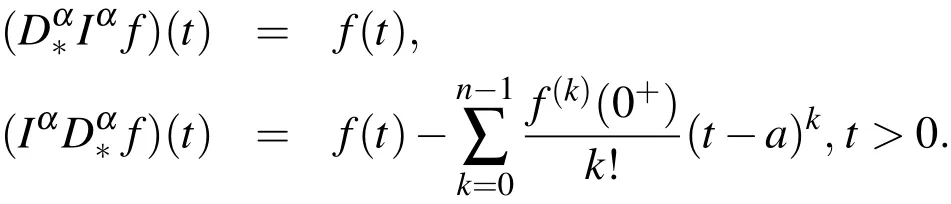
For comprehensive study on the properties of fractional derivatives and integrals,one can see for example,[Podlubny(1998)].

2.2 Some properties of ultraspherical polynomials and their shifted ones

The ultraspherical polynomials(x)(a special type of Jacobi polynomials)associated with the real parameter(λ ＞-),are a sequence of orthogonal polynomials defined on(-1,1),with respect to the weight functionThe orthogonality relation is given by

It should be noted here that the ultraspherical polynomials(x)are normalized such that(1)=1.This normalization is characterized by an advantage that the polynomials(x)are identical with the Chebyshev polynomials of the first kindTn(x),(x)are the Legendre polynomialsLn(x),and(x)are equal to(1/(n+1))Un(x),whereUn(x)are the Chebyshev polynomials of the second kind.The polynomials(x)may be generated by using the recurrence relation

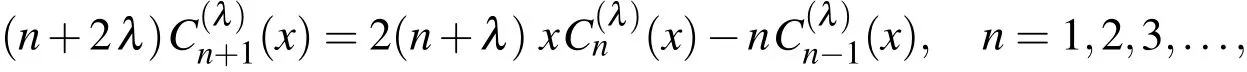
For more properties and relations of ultraspherical polynomials,see for instance[Andrews,Askey,and Roy(1999)].

The shifted ultraspherical polynomialsare a sequence of orthogonal polynomials defined on(0,1),with respect to the weight function˜w(x)=

They also may be generated by using the recurrence relation

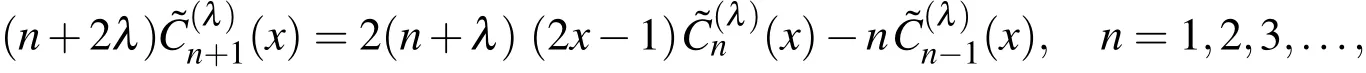
It is worthy to note here that,it is easy to transform all relations and properties of ultraspherical polynomials to give the corresponding relations and properties of the shifted ultraspherical polynomials.

Now,the following integral formula(see,[Andrews,Askey,and Roy(1999)])is needed

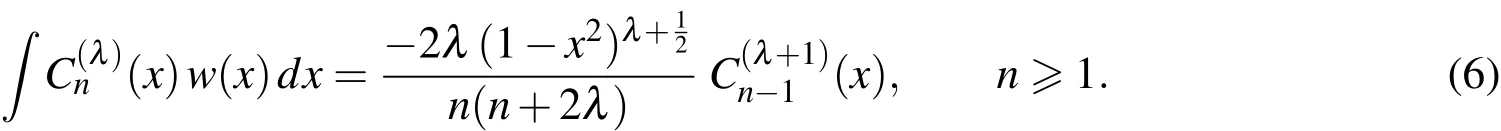
Also,the following theorem is essential in investigating the convergence analysis for the suggested ultraspherical wavelets expansion.

Theorem 1.(Bernstein-type inequality)[Giordano and Laforgia(2003)].The following inequality holds for ultraspherical polynomials:

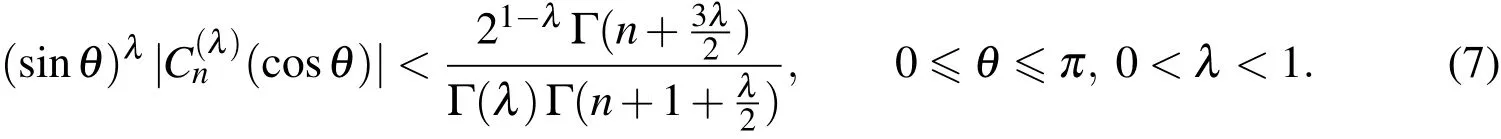
2.3 Ultraspherical wavelets

Wavelets constitute a family of functions constructed from dilation and translation of single function called the mother wavelet.When the dilation parameterAand the translation parameterBvary continuously,we have the following family of continuous wavelets:

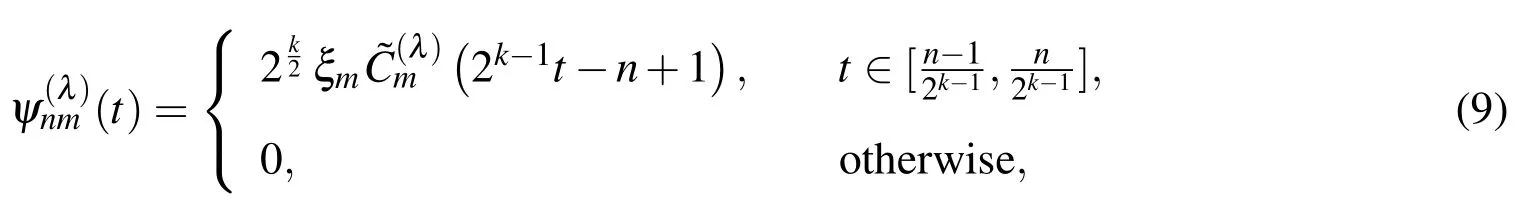
wherem=0(1)M-1，n=1(1)2k-1，and

Remark1.It is worthy noting here that(t)is identical to the Legendre waveletsin[Razzaghi and Yousefi(2000);Yousefi(2006)],(t)is identical to the first kind Chebyshev wavelets in[Babolian and Fattahzadeh(2007);Yuanlu(2010)]and(t)is identical to the second kind Chebyshev wavelets in[Maleknejad,Sohrabi,and Rostami(2007)].

Now,consider a functionf(t)defined on[0，1]and suppose thatf(t)may be expanded in terms of ultraspherical wavelets as

where

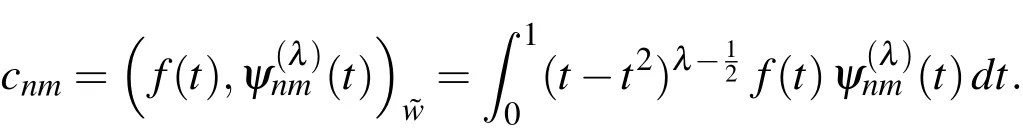
Assume thatf(t)is approximated in terms of ultraspherical wavelets as

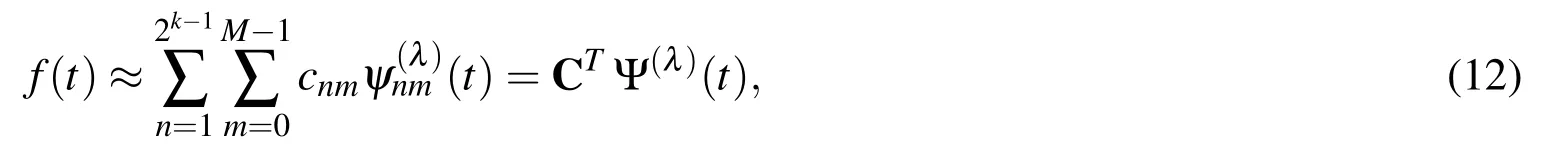
where C and Ψ(λ)(t)are 2k-1M× 1 matrices given by

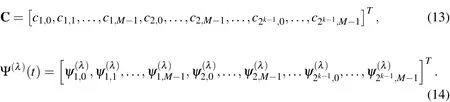
3 Convergence and error analysis

In this section,we give a comprehensive study on the convergence and error analysis of the suggested ultraspherical wavelets expansion.In this respect,we will state and prove two important theorems,in the first,we follow[Abd-Elhameed and Youssri(2014)]to show that the ultraspherical wavelets expansion of a functionf(x)with a bounded second derivative converges uniformly tof(x),and in the second,we give an upper bound for the error(innorm)of the truncated ultraspherical wavelets expansion.

The following lemma is needed.

Lemma 1.(see,[Stewart(2012)],p.742)Let f(x)be a continuous,positive,decreasing function for x≥n.If f(k)=ak，provided that∑anis convergent,and

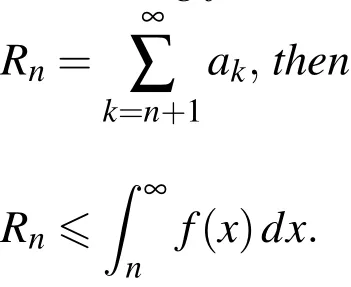
Theorem 2.A functioncan be ex-panded as an infinite series of ultraspherical wavelets,which converges uniformly to f(x)，given that|f′′(x)|≤L.Explicitly,the expansion coefficients in(12)satisfy the inequality

Proof.If we start with the definition(9)and apply the inner product of(t)to both sides of(12),then one can write the coefficientscnmin the form

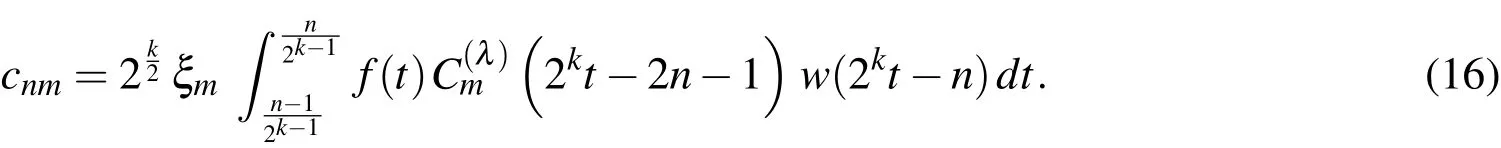
If the right hand side of(16)is integrated by parts,then in virtue of relation(6),Eq.(16)is turned into

Repeated use of integration by parts and making use of the substitution:2kt-2n-1=cosθ，enable one to write

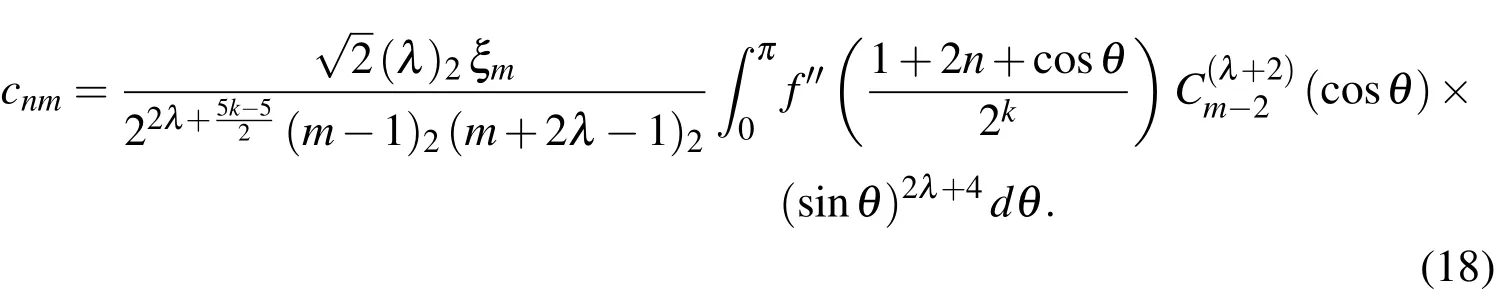
Now,assuming thatm＞ 2,taking into account the assumption|f′′(t)|≤L，and with the aid of Theorem 1,we obtain

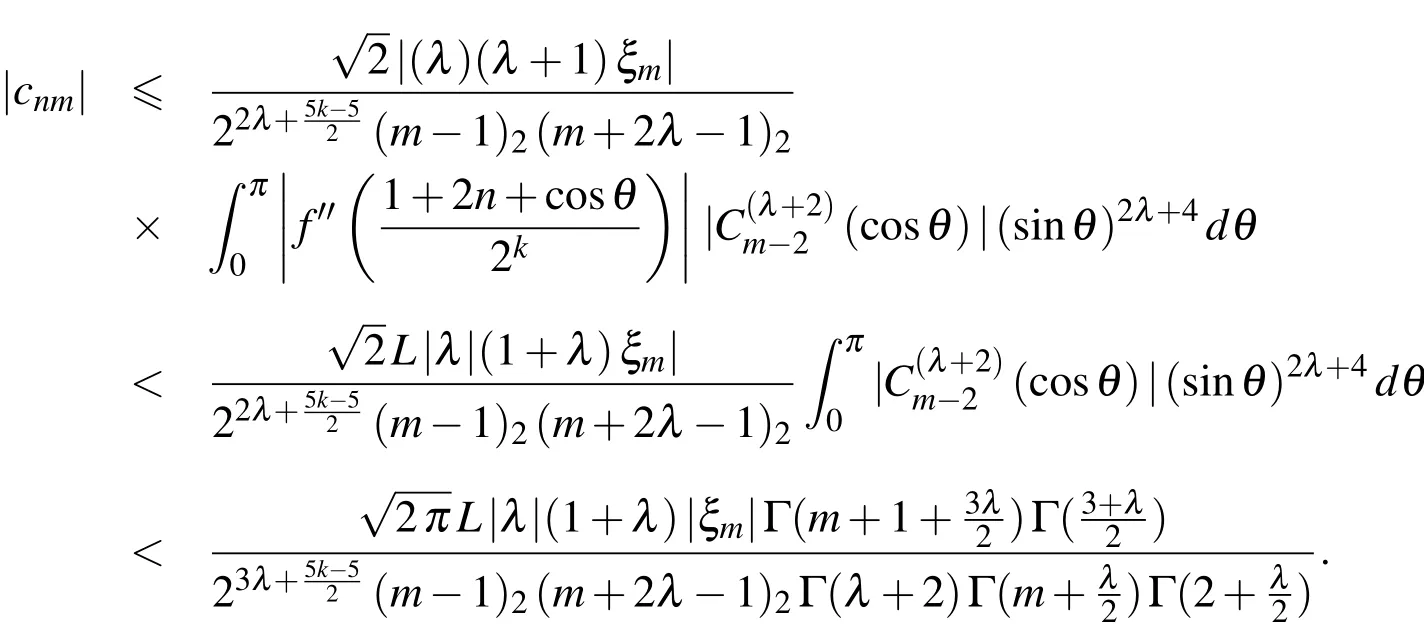
Since λ ＞ 0 andn＜ 2k-1，therefore with the aid of relation(10),we get

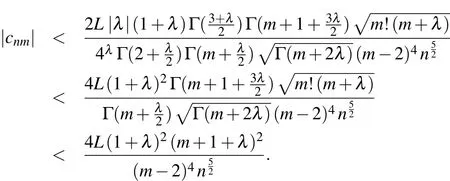
This completes the proof of the theorem.

Note.It should be noted here that,for large values ofmandn,and making use of the well known Stirling’s formula(see,[Li(2006)]),it can be easily shown thatis of

Theorem 3.If f，λsatisfy the hypothesis of Theorem 2,and if we consider theultraspherical wavelets expansion，then the followingerror estimate(innorm)is obtained

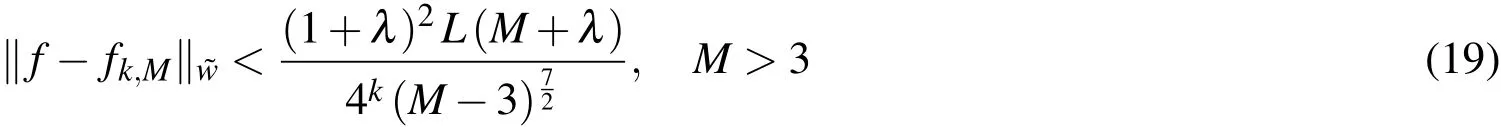
Proof.From Eq.(11),and making use of the orthonormality property ofwe get

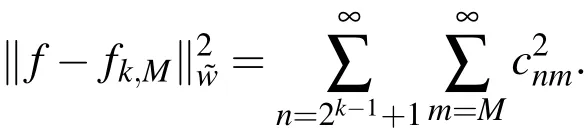
In virtue of Theorem 2,one can write

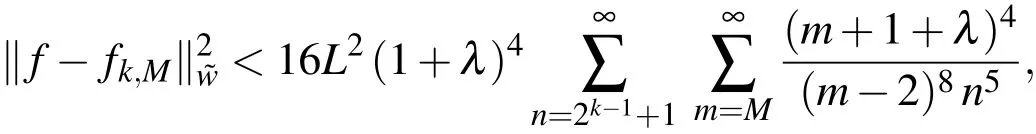
and the application of Lemma 1 leads to

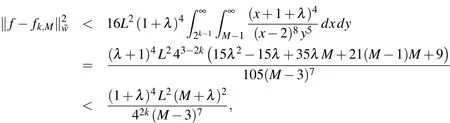
and hence

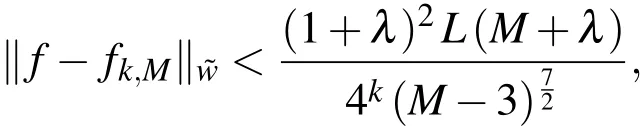
which completes the proof of the theorem.

Note.It should be noted here that,for large values ofkandM,it can be easily shown thatis of

4 Construction of ultraspherical wavelets operational matrix of the fractional integration(UWOMFI)

In this section,we describe in detail the derivation of the shifted ultraspherical wavelets operational matrix of the fractional integration.From now on,we setWe select the collocation pointstito be the zeros of the shifted ultraspherical polynomials of degreem′on the interval[0，1].We define the ultraspherical wavelets matrix Φm′×m′as

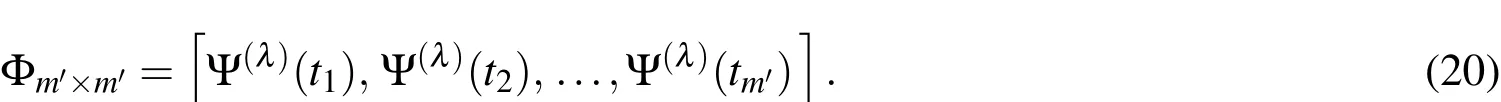
Correspondingly,we have

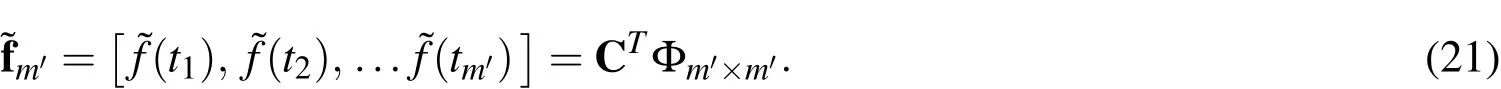
Since the shifted ultraspherical wavelets matrix Φm′×m′is an invertible matrix,the ultraspherical wavelets coefficient vector CTcan be obtained from the relation

Now,and if we assume thatf(t)can be expanded in terms of the shifted ultraspherical wavelets as in Eq.(12),then the Riemann-Liouville fractional integration in(1)becomes

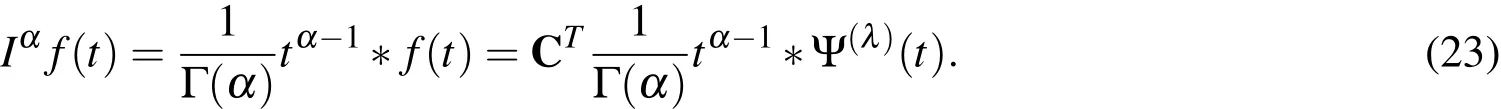
Thus iftα-1∗f(t)can be integrated,then expanded in the shifted ultraspherical wavelets,the Riemann-Liouville fractional integration is solved via the shifted ultraspherical wavelets.

Now,define the followingm-set of Block Pulse Function(BPF)on the interval[0，1)as(see,[Zhu and Fan(2012)])

wherei=0(1)m.The functionsbi(t)are disjoint and orthogonal,in the sense that

From the orthogonality property of BPF,it is possible to expand functions in terms of their block pulse series,so for everyf(t)∈ [0，1),one can write:

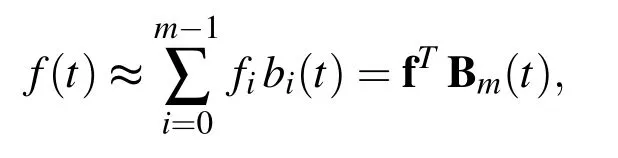
where

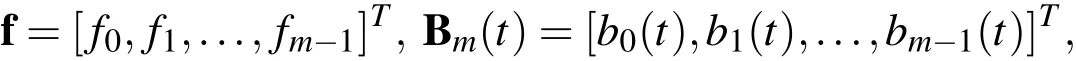
and

Similarly,the shifted ultraspherical wavelets may be expanded into anm′-term Block Pulse Functions as

The Block Pulse operational matrix of the fractional integrationFαis given by Kilicman in[Kilicman and Al Zhour(2007)].This matrix has the following explicit form

where

and

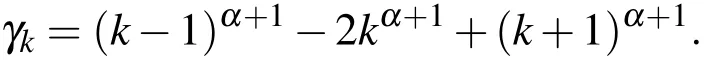
Now,for the sake of deriving the shifted ultraspherical wavelets operational matrix of the fractional integration,let

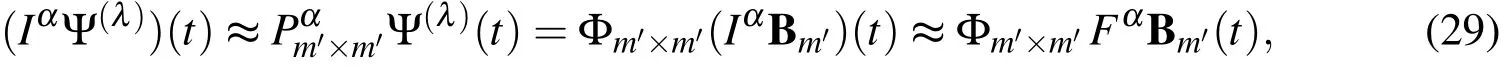
and consequently,Eqs.(28)and(29)lead to

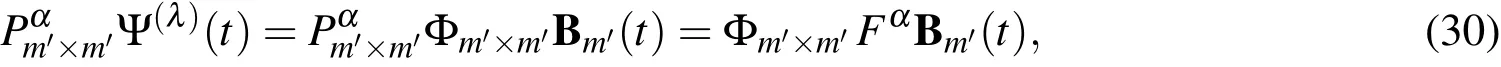
and therefore the ultraspherical wavelets operational matrix of the fractional integrationis given by

It should be noted that the operational matrixcontains many zero entries.This special structure,of course reduces the required computations.The calculation for the matrixis carried out once and is used to solve fractional order as well as integer order differential equations.

5 A new matrix algorithm for solving multi-term fractional-order differential equation

Consider the one-dimensional multi-term fractional-order differential equation

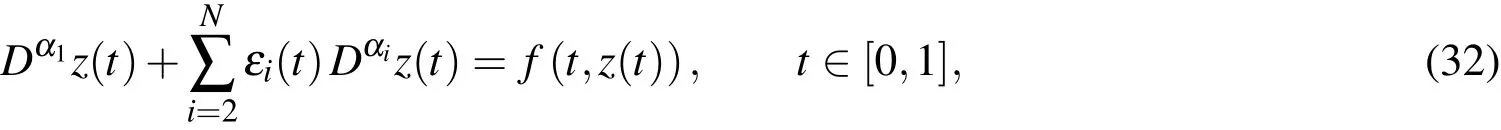
governed by the initial conditions

where

and εi:[0，1]→R，i=2(1)N，f:[0，1]×R→R is a given continuous function.The functionz(t)may be approximated by the ultraspherical wavelets as

Based on Eqs.(4),(29)and(34),we have the following approximations

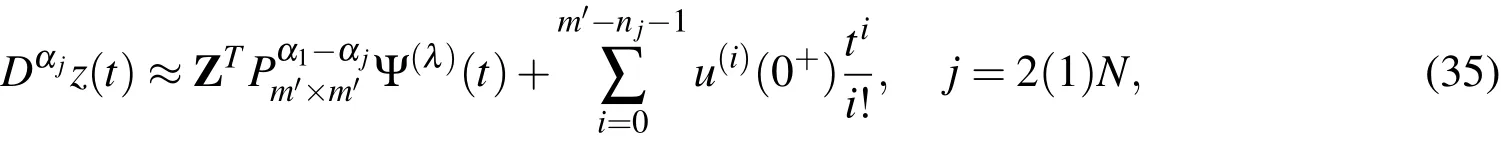
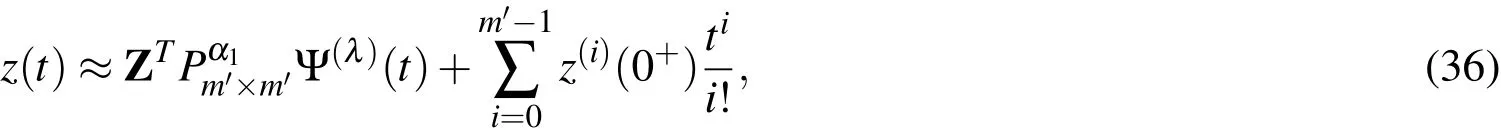
and hence the residual of Eq.(32)takes the form

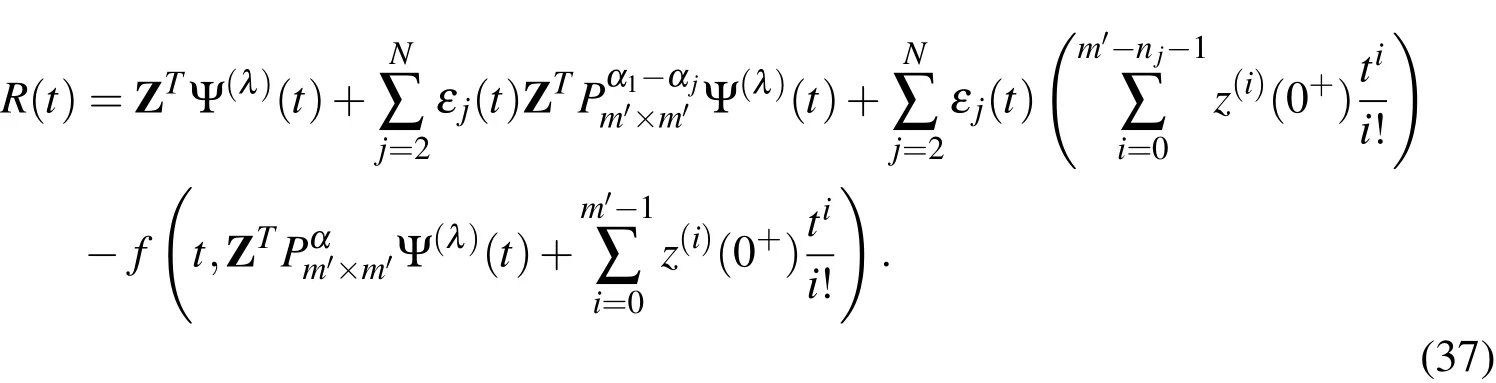
Now,Eq.(37)is enforced to be satisfied exactly at the pointstj，j=1(1)m′-n1which are selected to be the first(m′-n1)roots of the polynomial(t),then we have

Moreover,the initial conditions(33)yield

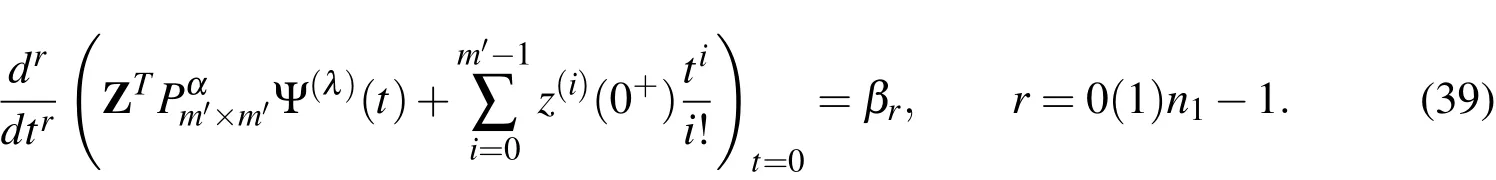
Eqs.(38)together with Eqs.(39)constitutem′nonlinear equations in the expansion coefficients,cnm，which can be solved with the aid of the well-known Newton’s iterative method.

6 Numerical examples

In this section,the ultraspherical wavelets collocation method(UWCM)which employs the operational matrix of fractional integration is applied for handling some numerical examples accompanied with some comparisons hoping to demonstrate the efficiency and applicability of the proposed algorithm.

Example 1.Consider the following nonlinear initial value problem(see,[Pedas and Tamme(2014)]):

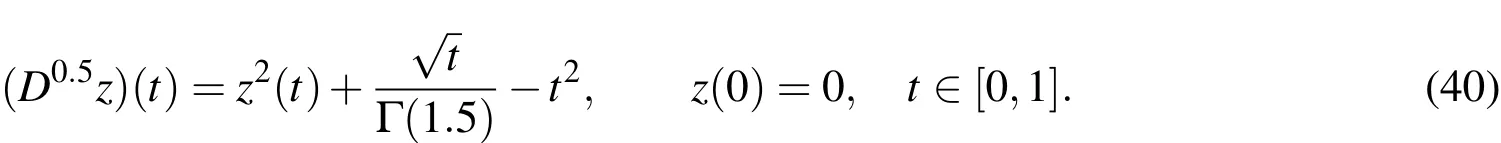
The exact solution of(40)is z(t)=t.We apply UWCM to Eq.(40)for the case

corresponding to k=1，M=2(m′=2)andλ =,The initial condition and theevaluation of the residual of Eq.(40)at the collocation pointyield thefollowing two equations

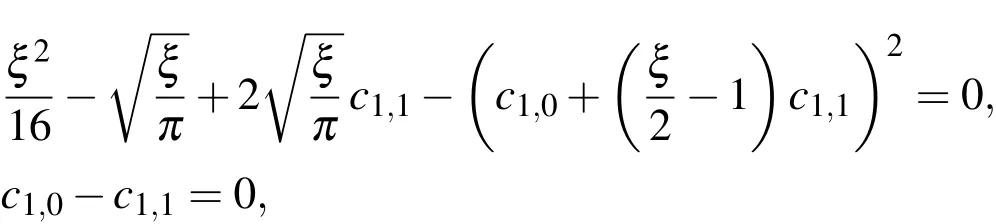
whereThis system can be solved to give

and consequently

which is the exact solution.

Example 2.Consider the following nonlinear initial value problem(see,[Sweilam,Khader,and Al-Bar(2007);Gejji and Jafari(2007);Saadatmandi and Dehghan(2010);Kazem,Abbasbandy,and Kumar(2013);Kazem(2013)]):

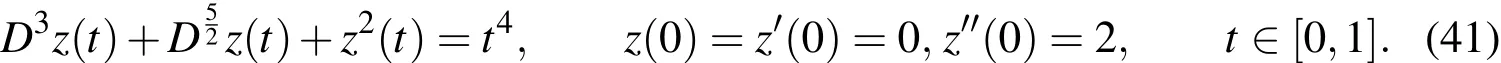
The exact solution of(41)is z(t)=t2.If UWCM is applied on Eq.(41),for the case corresponding to k=1，M=4(m′=4),andλ =1，then we have the following approximations

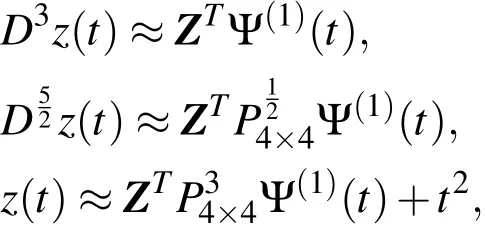
and hence the residual of Eq.(41)is given by

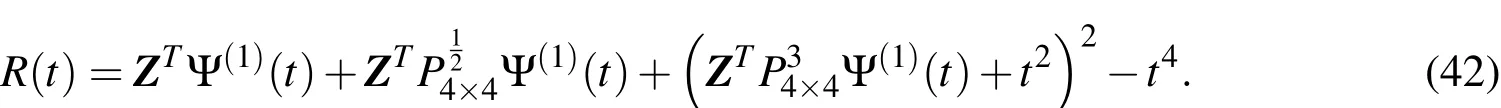
If R(t)is enforced to vanish at the collocation point，then the resultingequation jointly with the three equations resulted from the satisfaction of the initial conditions,yield a system of four equations whose solution is

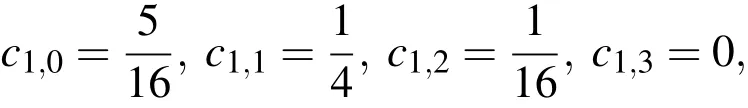
and consequently

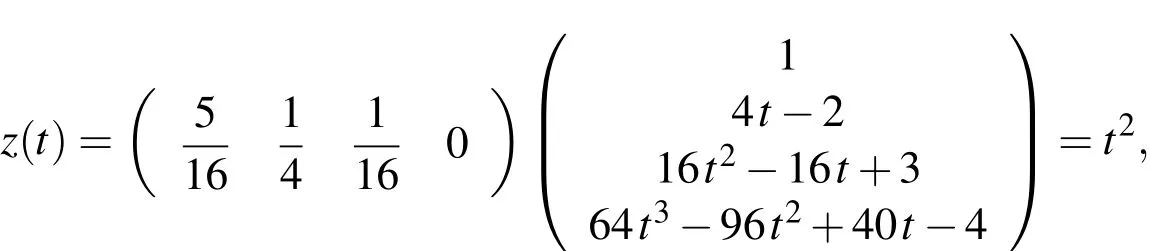
which is the exact solution.

Example3.Consider the following linear initial value problem(see,[Doha,Bhrawy,and Ezz-Eldien(2011);Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)]):

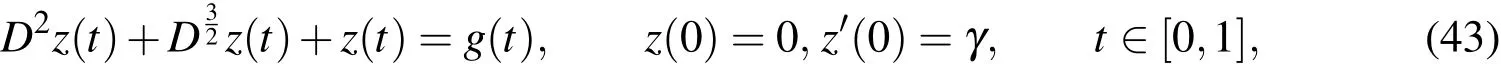
where g(t)is chosen such that the exact solution of(43)is z(t)=sin(γt).In Table 1,we display the maximum absolute error E resulted from the application of UWCM for the case k=2,with various choices of M，γandλ.In addition,Table 2 illustrates a comparison between the results obtained by UWCM with those obtained by using the following two methods:

•Shifted Chebyshev tau method(SCT)in[Doha,Bhrawy,and Ezz-Eldien(2011)].

•Shifted Jacobi tau method(SJT)in[Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)].

The results in Table 2 show that our algorithm is more accurate if compared with the two methods developed in[Doha,Bhrawy,and Ezz-Eldien(2011)]and[Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)].

Table 1:Maximum absolute error of Example 3

Example4.Consider the following linear initial value problem(see,[Doha,Bhrawy,and Ezz-Eldien(2011)]):

Table 2:Comparison between the best errors of Example 3

where g(t)is chosen such that the exact solution of(44)is z(t)=exp(γt).In Table 3,we list the maximum absolute errors E by using UWCM for the case k=3with various choices of M，γandλ.Moreover,in Table 4,we give a comparison between the present method with the shifted Chebyshev tau method(SCT)obtained in[Doha,Bhrawy,and Ezz-Eldien(2011)].In addition,in Figure 1,we illustrate the exact and numerical wavelets solutions for the case corresponding toγ=6，k=3，M=1and for various values ofλ.The results in Table 4 show that the error resulted from the application of our method are smaller than those obtained if SCT method in[Doha,Bhrawy,and Ezz-Eldien(2011)]is applied.

Table 3:Maximum absolute error of Example 4

Table 4:Comparison best errors of Example 4

Example 5.Consider the following linear initial value problem(see,[Bhrawy,

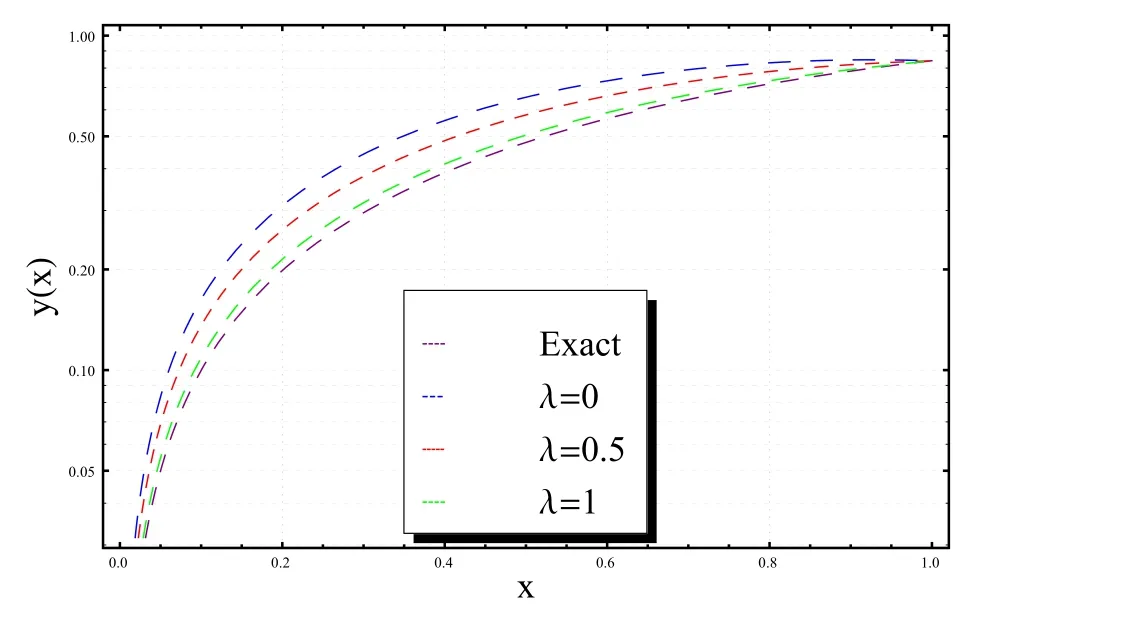
Figure 1:Different solutions of Example 4.

Alofi,and Ezz-Eldien(2011);Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)]):

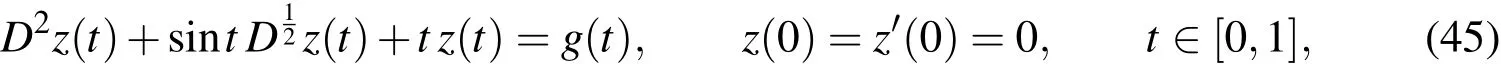
where

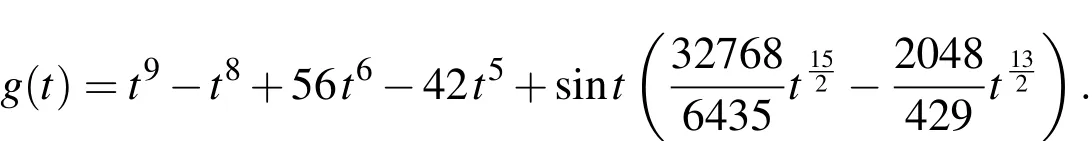
The exact solution for(45)is z(t)=t8-t7.In Table,5 we introduce the maximum absolute error E resulted from the application of UWCM for the case k=1，M=8(m′=8)with various choices ofλ,while in Table 6,we give a comparison between the best errors obtained from the application of UWCM with those obtained by the following two methods

•Quadrature shifted Legendre tau method(Q-SLT)in[Bhrawy,Alofi,and Ezz-Eldien(2011)].

•Quadrature shifted Jacobi tau method(Q-SJT)in[Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)].

Moreover,in Figure 2,we illustrate the exact and numerical wavelets solutions in case of k=1，M=8and for various values ofλ.

Remark 2.The results of Tables 3 and 5 ensure that the results corresponding to the first kind of Chebyshev wavelets expansion(in case ofλ=0)are not always better than the other expansions(see,[Doha and Abd-Elhameed(2005)]and[Light(1986)]).

Table 5:Maximum absolute error of Example 5

Table 6:Comparison between the best errors of Example 5

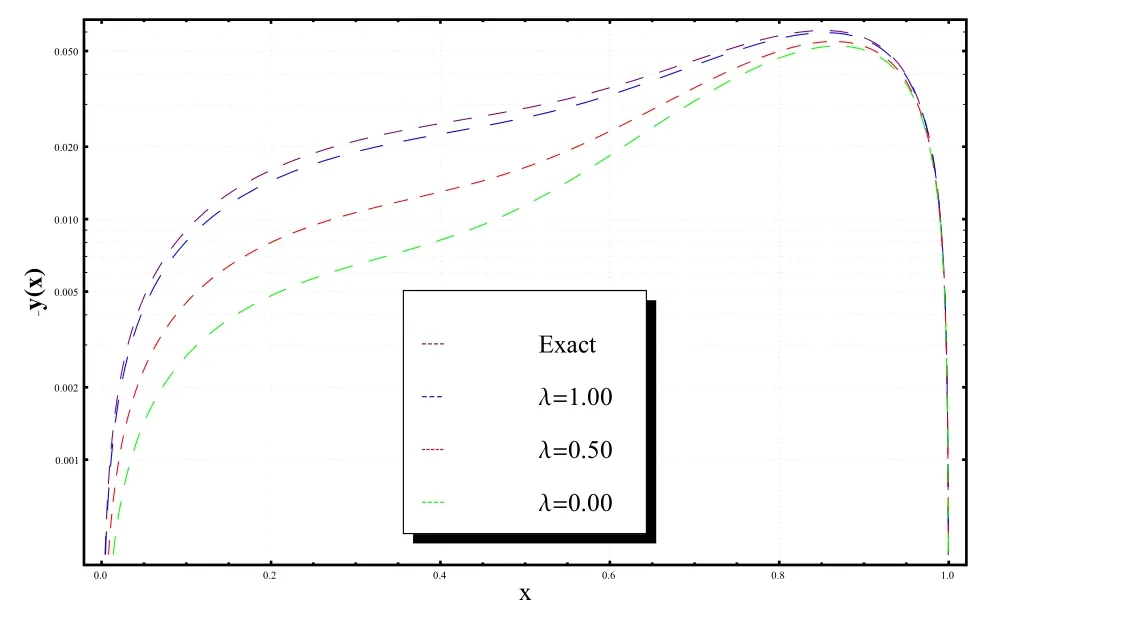
Figure 2:Different solutions of Example 5

Example 6.Consider the following nonlinear initial value problem(see,[Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)]):

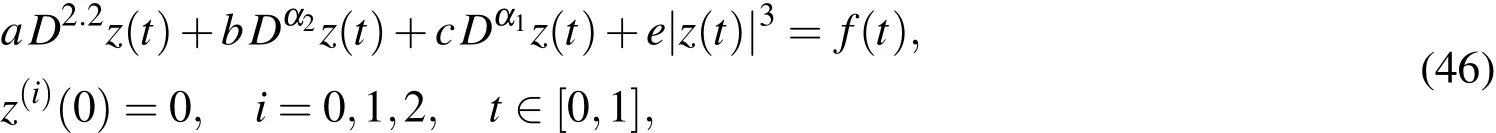
where

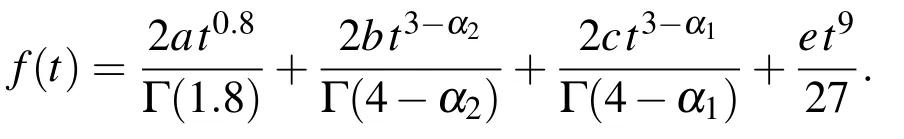
The exact solution of(46)is z(t)=.We apply UWCM to Eq.(46),for the casecorresponding to k=1，M=3(m′=3)andλ =.In this case

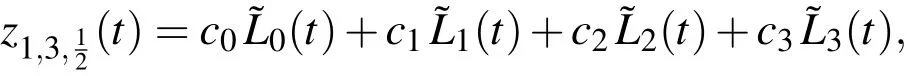
whereis the well-known shifted Legendre polynomial of degree i on[0，1]andWe solve Eq.(46)for a=b=c=e=1，α2=1.25，α1=0.75.(see,[Doha,Bhrawy,Baleanu,and Ezz-Eldien(2013)]).In this case,we have the following approximations

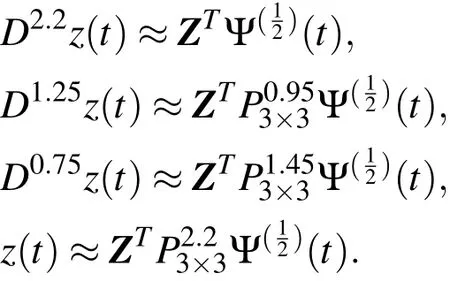
The residual of Eq.(46)is given by

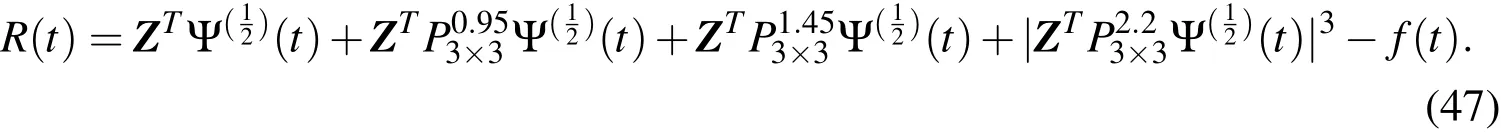
If Eq.(47)is collocated at the first root of L˜4(t),i.e,at t1=thenwe get

Moreover,the use of the initial conditions yield

The system of equations(48)-(51)can be solved to give

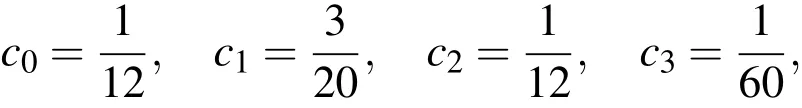
and consequently

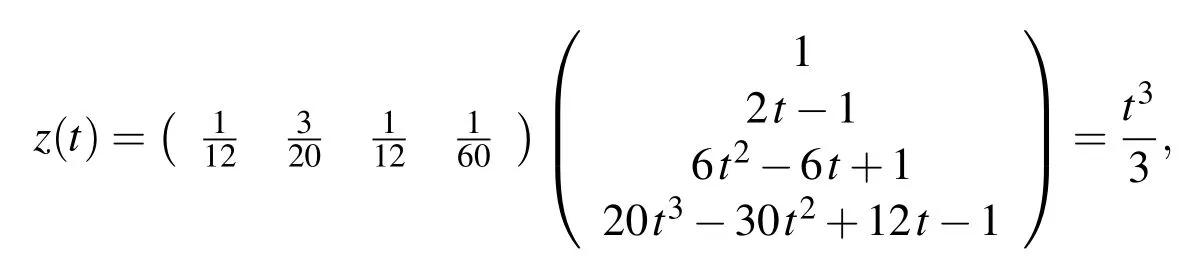
which is the exact solution.

7 Conclusions

In this paper,we have presented a new algorithm for obtaining some numerical spectral solutions for multi-term fractional-order initial value problems.The derivation of this algorithm is essentially based on constructing the ultraspherical wavelets operational matrix of the fractional integration.The convergence and error analysis of the suggested expansion is carefully investigated.One of the main advantages of the presented algorithm are its availability for application on both linear and non linear fractional-order initial value problems.Another advantage of the developed algorithm is its high accuracy since accurate approximate solutions can be achieved by using a few number of terms of the ultraspherical wavelets expansion.

Acknowledgement:The authors would like to thank the anonymous referees for carefully reading the manuscript and also for their valuable comments which improved the manuscript in its present form.

Abd-Elhameed,W.(2014):On solving linear and nonlinear sixth-order two point boundary value problems via an elegant harmonic numbers operational matrix of derivatives.CMES:Computer Modeling in Engineering&Sciences,vol.101,no.3,pp.159–185.

Abd-Elhameed,W.(2015):New Galerkin operational matrix of derivatives for solving Lane-Emden singular-type equations.The European Physical Journal Plus,vol.130,no.3,pp.1–12.

Abd-Elhameed,W.;Doha,E.;Youssri,Y.(2013a): Efficient spectral-Petrov-Galerkin methods for third-and fifth-order differential equations using general parameters generalized Jacobi polynomials.Quaestiones Mathematicae,vol.36,no.1,pp.15–38.

Abd-Elhameed,W.;Doha,E.;Youssri,Y.(2013b):New spectral second kind Chebyshev wavelets algorithm for solving linear and nonlinear second-order differential equations involving singular and Bratu type equations.Abstract and Applied Analysis,vol.2013.

Abd-Elhameed,W.;Youssri,Y.(2014):New ultraspherical wavelets spectral solutions for fractional Riccati differential equations.Abstract and Applied Analysis,vol.2014,Article ID 626275,8 pages.

Al-Mdallal,Q.;Syam,M.I.;Anwar,M.(2010):A collocation-shooting method for solving fractional boundary value problems.Communications in Nonlinear Science and Numerical Simulation,vol.15,no.12,pp.3814–3822.

Andrews,G.;Askey,R.;Roy,R.(1999):SpecialFunctions.Cambridge University Press,Cambridge.

Arikoglu,A.;Ozkol,I.(2009): Solution of fractional integro-differential equations by using fractional differential transform method.Chaos,Solitons&Fractals,vol.40,no.2,pp.521–529.

Babolian,E.;Fattahzadeh,F.(2007): Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration.Applied Mathematics and computation,vol.188,no.1,pp.417–426.

Bhrawy,A.;Alofi,A.;Ezz-Eldien,S.(2011): A quadrature tau method for variable coefficients fractional differential equations.Applied Mathematics Letters,vol.24,no.12,pp.2146–2152.

Brunner,H.;Pedas,A.;Vainikko,G.(2001):Piecewise polynomial collocation methods for linear Volterra integro-differential equations with weakly singular kernels.SIAM Journal on Numerical Analysis,vol.39,no.3,pp.957–982.

Çenesiz,Y.;Keskin,Y.;Kurnaz,A.(2010):The solution of the Bagley–Torvik equation with the generalized Taylor collocation method.Journal of the Franklin Institute,vol.347,no.2,pp.452–466.

Costabile,F.;Napoli,A.(2015):Collocation for high order differential equations with two-points Hermite boundary conditions.Applied Numerical Mathematics,vol.87,pp.157–167.

Daftardar-Gejji,V.;Jafari,H.(2005): Adomian decomposition:a tool for solving a system of fractional differential equations.Journal of Mathematical Analysis and Applications,vol.301,no.2,pp.508–518.

Das,S.(2009):Analytical solution of a fractional diffusion equation by variational iteration method.Computers&Mathematics with Applications,vol.57,no.3,pp.483–487.

Diethelm,K.(2010):The analysis of fractional differential equations:An application-oriented exposition using differential operators ofCaputo type,volume 2004.Springer Science&Business Media.

Doha,E.;Abd-Elhameed,W.(2002):Efficient spectral-Galerkin algorithms for direct solution of second-order equations using ultraspherical polynomials.SIAM Journal on Scientific Computing,vol.24,no.2,pp.548–571.

Doha,E.;Abd-Elhameed,W.(2005): Accurate spectral solutions for the parabolic and elliptic partial differential equations by the ultraspherical tau method.Journal of computational and applied mathematics,vol.181,no.1,pp.24–45.

Doha,E.;Bhrawy,A.;Baleanu,D.;Ezz-Eldien,S.(2013):On shifted Jacobi spectral approximations for solving fractional differential equations.Applied Mathematics and Computation,vol.219,no.15,pp.8042–8056.

Doha,E.;Bhrawy,A.;Ezz-Eldien,S.(2011): Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations.Applied Mathematical Modelling,vol.35,no.12,pp.5662–5672.

Elgindy,K.;Smith-Miles,K.(2013a):On the optimization of Gegenbauer operational matrix of integration.Advances in Computational Mathematics,vol.39,no.3-4,pp.511–524.

Elgindy,K.;Smith-Miles,K.(2013b): Solving boundary value problems,integral,and integro-differential equations using Gegenbauer integration matrices.Journal of Computational and Applied Mathematics,vol.237,no.1,pp.307–325.

Elgohary,T.;Dong,L.;Junkins,J.;Atluri,S.(2014): Time domain inverse problems in nonlinear systems using collocation&radial basis functions.CMES:Computer Modeling in Engineering&Sciences,vol.100,no.1,pp.59–84.

Erturk,V.;Momani,S.;Odibat,Z.(2008): Application of generalized differential transform method to multi-order fractional differential equations.Communications in Nonlinear Science and Numerical Simulation,vol.13,no.8,pp.1642–1654.

Gejji,V.;Jafari,H.(2007):Solving a multi-order fractional differential equation.Applied Mathematics and Computation,vol.189,pp.541–548.

Giordano,C.;Laforgia,A.(2003):On the Bernstein-type inequalities for ultraspherical polynomials.Journal of computational and applied mathematics,vol.153,no.1,pp.243–248.

Jafari,H.;Seifi,S.(2009):Solving a system of nonlinear fractional partial differential equations using homotopy analysis method.Communications in Nonlinear Science and Numerical Simulation,vol.14,no.5,pp.1962–1969.

Kazem,S.(2013):An integral operational matrix based on Jacobi polynomials for solving fractional-order differential equations.Applied Mathematical Modelling,vol.37,no.3,pp.1126–1136.

Kazem,S.;Abbasbandy,S.;Kumar,S.(2013): Fractional-order Legendre functions for solving fractional-order differential equations.Applied Mathematical Modelling,vol.37,no.7,pp.5498–5510.

Kilbas,A.;Marichev,O.;Samko,S.(1993):Fractional integrals and derivatives(theory and applications).Gordon and Breach,Switzerland.

Kilbas,A.;Srivastava,H.;Trujillo,J.(2006):Theory and applications of fractional differential equations,volume 204.Elsevier Science Limited.

Kilicman,A.;Al Zhour,Z.(2007):Kronecker operational matrices for fractional calculus and some applications.Applied Mathematics and Computation,vol.187,no.1,pp.250–265.

Li,Y.(2006):A note on an identity of the gamma function and Stirling’s formula.Real Analysis Exchange,vol.32,no.1,pp.267–272.

Light,W.(1986): Are Chebyshev expansions really better?Bulletin of the Institute of Mathematics and its Applications,vol.22,pp.180–181.

Maleknejad,K.;Sohrabi,S.;Rostami,Y.(2007):Numerical solution of nonlinear Volterra integral equations of the second kind by using Chebyshev polynomials.Applied Mathematics and Computation,vol.188,no.1,pp.123–128.

Momani,S.(2007):An algorithm for solving the fractional convection–diffusion equation with nonlinear source term.Communications in Nonlinear Science and Numerical Simulation,vol.12,no.7,pp.1283–1290.

Pedas,A.;Tamme,E.(2014): Numerical solution of nonlinear fractional differential equations by spline collocation methods.Journal of Computational and Applied Mathematics,vol.255,pp.216–230.

Podlubny,I.(1998):Fractional Differential Equations:an introduction to fractional derivatives,fractional differential equations,to methods of their solution and some of their applications,volume 198.Academic press.

Razzaghi,M.;Yousefi,S.(2000): Legendre wavelets direct method for variational problems.Mathematics and Computers in Simulation,vol.53,no.3,pp.185–192.

Saadatmandi,A.;Dehghan,M.(2010): A new operational matrix for solving fractional-order differential equations.Computers&Mathematics with applications,vol.59,no.3,pp.1326–1336.

Sadek,I.;Abualrub,T.;Abukhaled,M.(2007): A computational method for solving optimal control of a system of parallel beams using Legendre wavelets.Mathematical and Computer Modelling,vol.45,no.9,pp.1253–1264.

Stewart,J.(2012):Single Variable Essential Calculus:Early Transcendentals.Cengage Learning.

Sweilam,N.;Khader,M.;Al-Bar,R.(2007):Numerical studies for a multi-order fractional differential equation.Physics Letters A,vol.371,no.1,pp.26–33.

Wang,J.;Liu,L.;Chen,Y.;Liu,L.;Liu,D.(2015): Numerical study for a class of variable order fractional integral-differential equation in terms of Bernstein polynomials.CMES:Computer Modeling in Engineering&Sciences,vol.105,no.1,pp.69–85.

Yousefi,S.(2006): Legendre wavelets method for solving differential equations of Lane–Emden type.Applied Mathematics and Computation,vol.181,no.2,pp.1417–1422.

Yuanlu,L.(2010): Solving a nonlinear fractional differential equation using Chebyshev wavelets.Communications in Nonlinear Science and Numerical Simulation,vol.15,no.9,pp.2284–2292.

Zhu,L.;Fan,Q.(2012): Solving fractional nonlinear Fredholm integrodifferential equations by the second kind Chebyshev wavelet.Communications in Nonlinear Science and Numerical Simulation,vol.17,no.6,pp.2333–2341.

1Department of Mathematics,Faculty of Science,University of Jeddah,Jeddah,Saudi Arabia.

2Department of Mathematics,Faculty of Science,Cairo University,Giza 12613,Egypt.