Finding the Generalized Solitary Wave Solutions within the(G′/G)-Expansion Method

K.Sayevand,Yasir Khan,E.Moradiand M.Fardi

Finding the Generalized Solitary Wave Solutions within the(G′/G)-Expansion Method

K.Sayevand1,Yasir Khan2,E.Moradi3and M.Fardi4

In this study,the solitary wave solutions for third order equal-width wave-Burgers(EW-Burgers)equation,the second order Bratu and sinh-Bratu type equations will be discussed.The EW-Burgers equation models the propagation of nonlinear and dispersive waves with certain dissipative effects and furthermore the Bratu type problem appears a simplification of the solid fuel ignition model in thermal combustion theory.Our methodology,is investigated by using(G′/G)-expansion method.The obtained results can be extended to the other models.

(G′/G)-expansion method,Nonlinear evolution equations,EW-Burgers equation,Bratu and sinh-Bratu type equations.

1 Introduction

It is well known that most of the phenomena that appear in physics can be described by partial differential equations Ebaid(2007),Bekir and Boz(2008),Yan(1996),Parkes(2010)and Ramos(2006).In this paper,the following problems will be investigated:

a.Canonical EW-Burgers equation as a special case of the generalized regularized long-wave(GRLW)equation which can be written as following

where α,γ,δ and β are given non-negative real constants andp≥ |t|+2，is a constant.

The equal width wave equation is a model partial differential equation for the simulation of one-dimensional wave propagation in nonlinear media with dispersion processes.This equation is an important mathematical model arising in many different physical contexts to describe many phenomena which are simultaneously involved in nonlinearity,dissipation,dispersion,and instability,especially at the description of turbulence processes Ebaid(2007).

b.The nonlinear second order Bratu and sinh-Bratu type equations in the following form

The The Bratu type problem can be used as the model of thermal reaction process,chemical reaction theory,radiative heat transfer and nanotechnology to the expansion of universe Wazwaz(2005),Abbasbandy,Hashemi,and Liu(2011)and Boyd(2011).The solving procedure of this method,by the help of Maple,Matlab,or any Mathematical package,is of utter simplicity.

Recently,several direct methods such as Exp-function method Bekir and Boz(2008)and Yan(1996),sine-cosine method Parkes(2010),tanh-coth method Wang,Zhou,and Li(1996),the homogeneous balance method Wang and Li(2005b),F-expansion method Wang and Li(2005a)and also wavelet methods Ray and Gupta(2014);Gupta and Ray(2014)have been proposed to obtain exact solutions of nonlinear partial differential equations.Using these methods many exact solutions,including the solitary wave solutions,shock wave solutions and periodic wave solutions are obtained for some kinds of nonlinear evolution equations.

The application of(G′/G)-expansion method to obtain more explicit traveling wave solutions to many nonlinear differential equations has been developed by many researchers Wang,Zhang,and Li(2008),Zayed and Gepreel(2009)Aslan and Özi¸s(2009)and Bekir(2008).The(G′/G)-expansion method is based on the assumption that the travelling wave solutions can be expressed by a polynomial in(G′/G).It has been shown that this method is straightforward,concise,basic and effective.Eq.(1)and Eq.(2)for different values of α，β，δ，γ andpare presented in Table 1 and Table 2 respectively.Finally,the paper is organized as follows.In the next section,the basic(G′/G)-expansion method is introduced.Application ofG′/G-expansion method to our equations is presented in Section 3.Section 4 ends this work with a brief conclusion.

2 The basic(G′/G)-expansion method

We suppose that the given nonlinear partial differentialu(x，t)to be in the form

Table 1:Eq.(1)for different values of α，β，δ，γ and p

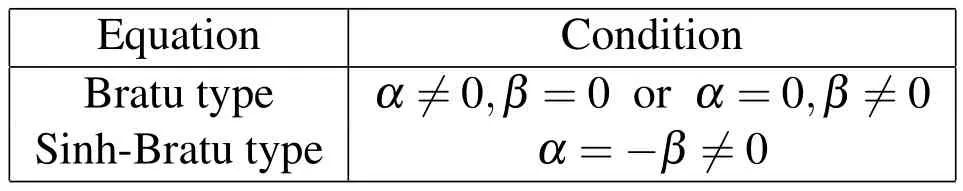
Table 2:Eq.(2)for different values of α，β，δ，γ and p

wherePis a multivariate polynomial in its arguments.In the following,it is explained the essential steps for implementing(G′/G)-expansion method.

Step 1.Taking the change of variable ξ =x-wt，givesu(x，t)=U(ξ),wherewis a constant parameter to be determined later.Substituting ξ=x-wtinto the Eq.(3)yields an ODE forU(ξ)of the form

Step 2.Introduce the approach

whereG=G(ξ)satisfies the differential equation

hereNis a positive integer(to be determined).Thebj，j=0，···，Nand λ and µ are real constants withbN/=0,and the prime denotes derivative with respect to ξ.(G′/G)satisfies the differential equation

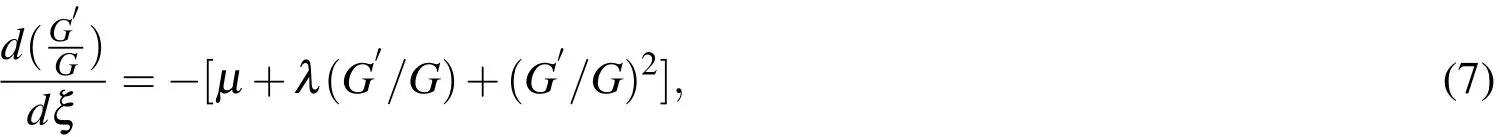
and so,

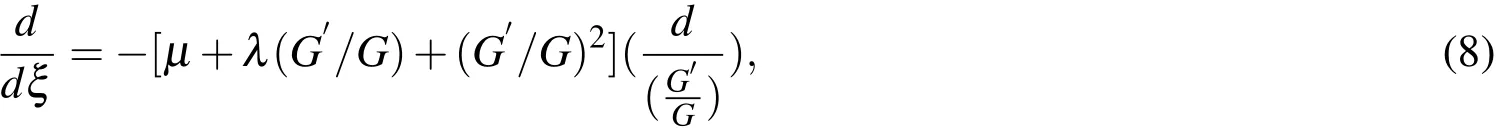
and

Substituting Eq.(5)and(8)and(9)into the ODE from step 1,yields an algebraic equation in powers of the(G′/G).Then,the positive integerNis determined by the balance of linear and nonlinear terms of the highest order in the resulting algebraic equation.

Step 3.WithNbeing determined,the coefficients of each power of(G′/G)in the algebraic equation from Step 2 put equal to zero.This yields a system of algebraic equations involvingbj，j=0，...，N，wand the integration constants.Finally,the general solution of Eq.(6)is to be substituted into Eq.(5).

3 Application of G′/G-expansion method to EW-Burgers equation

To look for travelling wave solutions of Eq.(1),we use the wave transformation ξ=x-wtand change Eq.(2)into the form of an ODE

Integrating it with respect to ξ and setting the constant of integration to zero,we obtain

Now,we make an approach Eq.(6)for the solution of Eq.(10).Balancing the termsU2andU′′in Eq.(11),then we get 2N=N+2 which yields the leading term orderN=2.Therefore,we can write the solution of Eq.(11)in the form

Substituting Eq.(12)into Eq.(11),collecting the coefficients ofand set it to zero we obtain the system of algebraic equations forb0，b1，b2andw.Then,solving the system by Mathematica 7.,we obtain the following answers

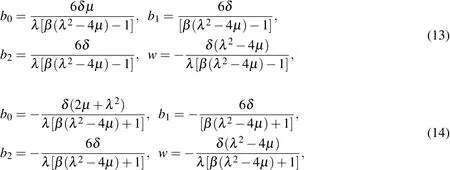
where λ and µ are arbitrary constants.Substituting Eqs.(13)and(14)into Eq.(12)yields

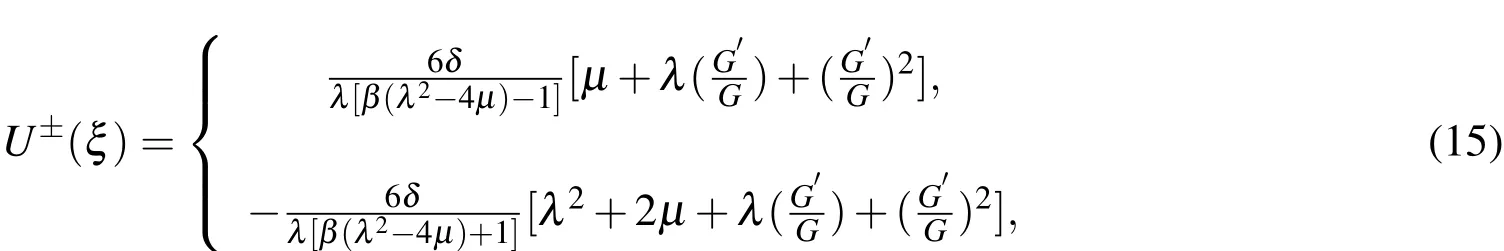
1.when λ2-4µ ＞ 0，we have

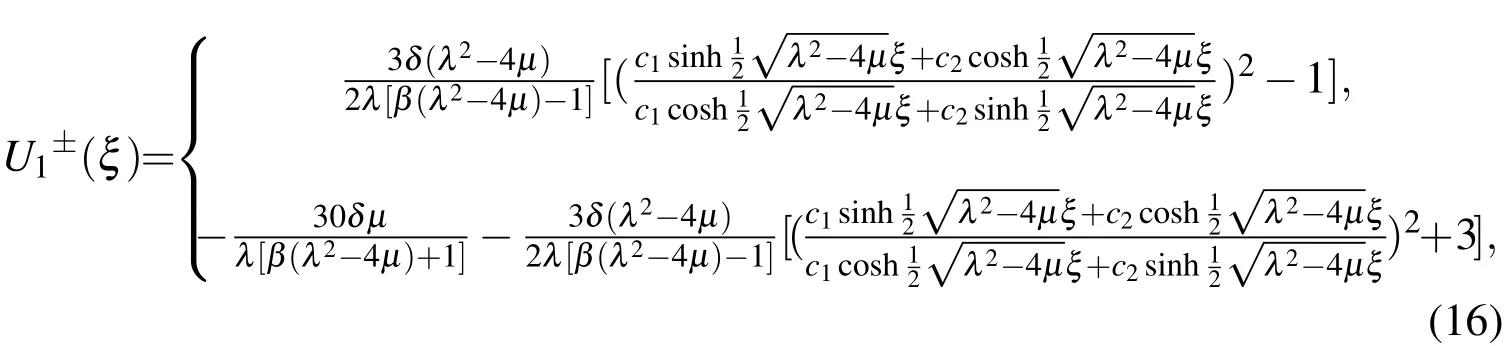
2.when λ2-4µ ＜ 0，we have

3.when λ2-4µ =0，we have

wherec1，c2in Eq.(16),d1，d2in Eq.(17)andx0in Eq.(18)are arbitrary real constants.

4 Application of G′/G-expansion method to Bratu and sinh-Bratu type equations

4.1 The Bratu type equations

We first consider the Bratu type equations

To look for solutions of Eq.(28),we use the wave transformation ξ=kx+x0and change Eq.(28)into the form of an ODE

Using the transformationU(ξ)=lnv(ξ),will change Eq.(29)into the ODE in the form

substituting Eqs.(8),(9)and(13)into Eq.(12),collecting the coefficients of，and set it to zero we obtain a system of algebraic equations forb0，b1，b2andk，that solving this system by Mathematica 7.gives

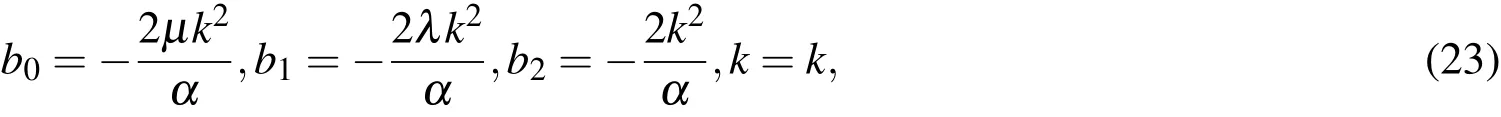
where λ and µ are arbitrary constants.Substituting Eq.(31)into Eq.(12)yields

where ξ=kx+x0.Substituting the general solutions of Eq.(5)into Eq.(15)we have three types of solutions of the Bratu type equations as follows

1.When λ2-4µ ＞ 0，we have

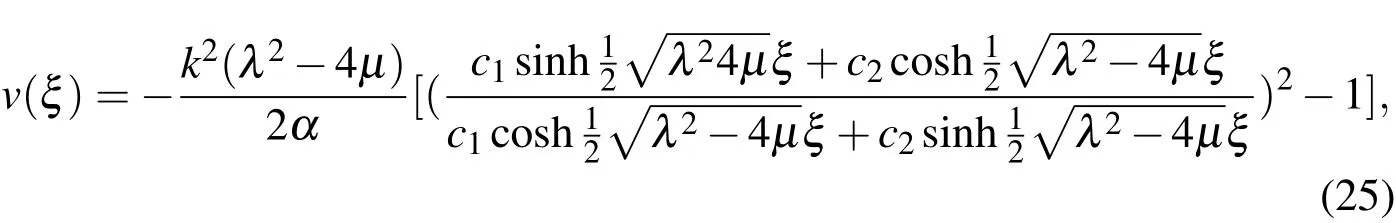
2.When λ2-4µ ＜ 0,we have

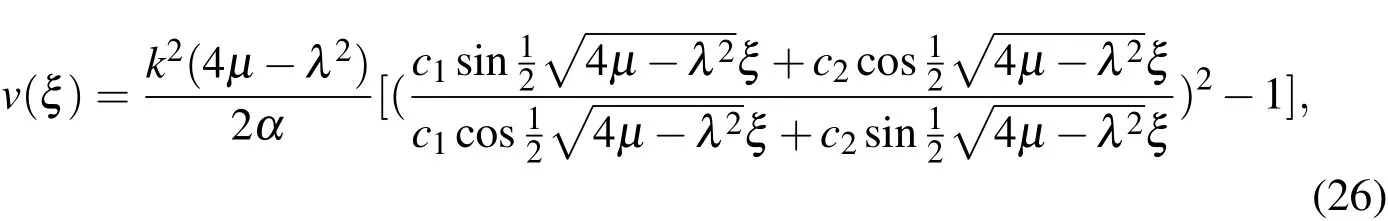
3.When λ2-4µ =0，we have

where ξ =kx+x0，c1andc2in Eqs.(16)and(17),andin Eq.(18)are arbitrary constants.In particular,if we choosec2/=0，c12＜c22then the solution Eq.(16)give the solution

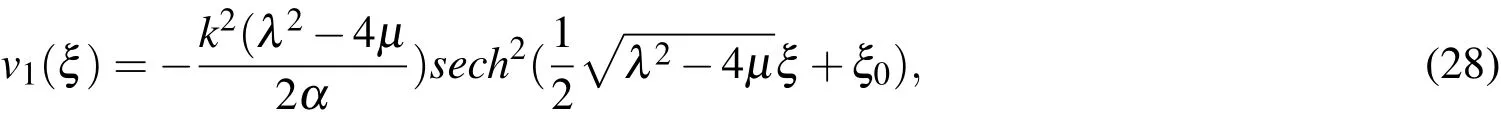
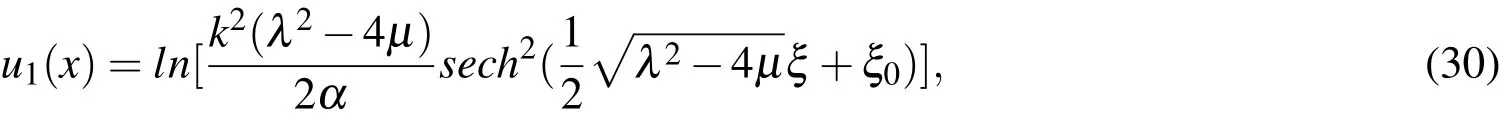
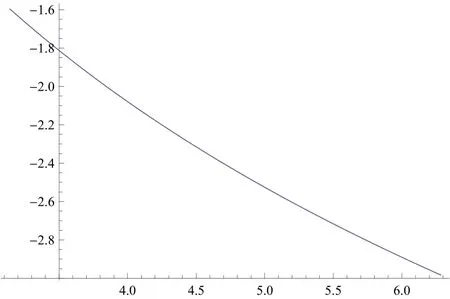
Figure 1:Approximate solution of Eq.(20)where α =-1 and x ∈ [1，2].

4.2 The sinh-Bratu type equations

We secondly consider sinh-Bratu type equations

Figure 2:Approximate solution of Eq.(20)where α =-1.5 and x∈ [1，2].

In order to apply the(G′/G)method,we use the transformation ξ =kx+x0and change Eq.(33)into the form

And then we use the transformationU(ξ)=lnv(ξ),so that

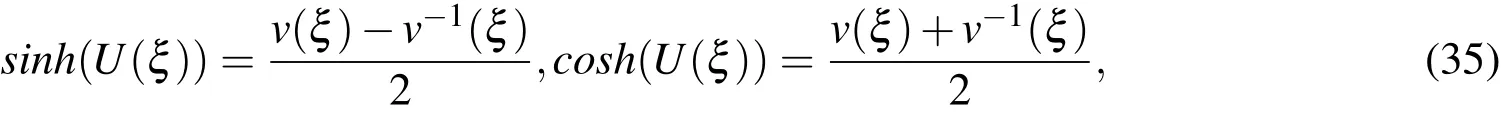
this transformation will change Eq.(34)into the ODE in the form

substituting Eqs.(8),(9)and(37)into Eq.(36),collecting the coefficients of，and set it to zero we obtain a system of algebraic equations forb0，b1，b2andk.By solving the resulted system with the help of Mathematca 7.we have the following sets of solutions

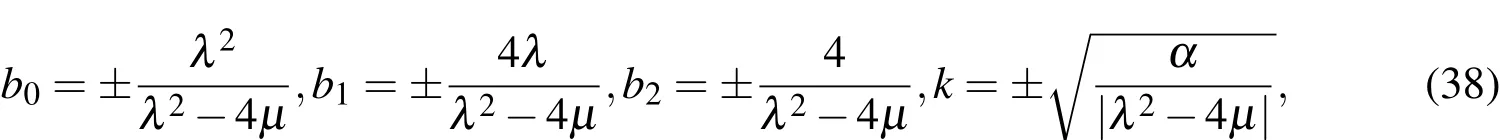
where λ,µ and λ2/=4µ are arbitrary constants.Substituting Eq.(38)into Eq.(37)yields

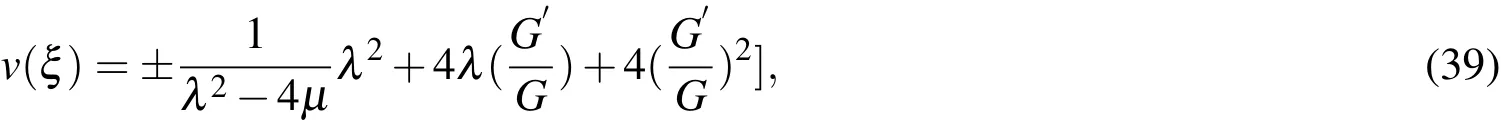
where ξ=kx+x0.By substituting the general solutions of Eq.(5)into Eq.(39)we have three types of solutions of the sinh-Bratu type equations as follows

1.When λ2-4µ ＞ 0，we have

2.When λ2-4µ ＜ 0,we have

In particular,if we choosec2/=0，c12＜c22then the solutions Eqs.(40)and(41)give the following solutions

Figure 3:Approximate solution of Eq.(33)where µ =0.125，λ =0.7，k=1，x0=0，ξ0=1 and x∈ [π，2π]

Figure 4:Approximate solution of Eq.(33)where µ =0.125，λ =0.7，k=1，x0=0，ξ1=1 and x∈ [π，2π].

Remark:The computations associated in Figures[1-4]were performed by using Mathematica 7.

5 Conclusions

In this paper,we apply the(G′/G)-expansion method to third order EW-Burgers equation and Bratu and sinh-Bratu type equations.Our results show that the(G′/G)-expansion method is entirely efficient and well suited for finding exact solutions of these equation.The advantage of this method over other methods is that we can obtain the exact solution by using a simple computer program.

Abbasbandy,S.;Hashemi,M.;Liu,C.-S.(2011): The lie-group shooting method for solving the bratu equation.Communications in Nonlinear Science and Numerical Simulation,vol.16,no.11,pp.4238–4249.

Aslan,˙I.;Özi¸s,T.(2009):On the validity and reliability of the(g′/g)-expansion method by using higher-order nonlinear equations.Applied Mathematics and Computation,vol.211,no.2,pp.531–536.

Bekir,A.(2008): Application of the-expansion method for nonlinear evolution equations.Physics Letters A,vol.372,no.19,pp.3400–3406.

Bekir,A.;Boz,A.(2008):Exact solutions for nonlinear evolution equations using exp-function method.Physics Letters A,vol.372,no.10,pp.1619–1625.

Boyd,J.P.(2011):One-point pseudospectral collocation for the one-dimensional bratu equation.Applied Mathematics and Computation,vol.217,no.12,pp.5553–5565.

Ebaid,A.(2007): Exact solitary wave solutions for some nonlinear evolution equations via exp-function method.Physics Letters A,vol.365,no.3,pp.213–219.

Gupta,A.;Ray,S.S.(2014):Traveling wave solution of fractional kdv-burgerkuramoto equation describing nonlinear physical phenomena.AIP Advances,vol.4,no.9,pp.097120.

Parkes,E.(2010):Observations on the tanh–coth expansion method for finding solutions to nonlinear evolution equations.Applied Mathematics and Computation,vol.217,no.4,pp.1749–1754.

Ramos,J.(2006):Explicit finite difference methods for the ew and rlw equations.Applied mathematics and computation,vol.179,no.2,pp.622–638.

Ray,S.S.;Gupta,A.(2014):An approach with haar wavelet collocation method for numerical simulations of modified kdv and modified burgers equations.CMES:Computer Modeling in Engineering&Sciences,vol.103,no.5,pp.315–341.

Wang,M.;Li,X.(2005):Applications of f-expansion to periodic wave solutions for a new hamiltonian amplitude equation.Chaos,Solitons&Fractals,vol.24,no.5,pp.1257–1268.

Wang,M.;Li,X.(2005): Extended f-expansion method and periodic wave solutions for the generalized zakharov equations.Physics Letters A,vol.343,no.1,pp.48–54.

Wang,M.;Zhang,J.;Li,X.(2008):Application of the-expansion to travelling wave solutions of the broer–kaup and the approximate long water wave equations.Applied Mathematics and Computation,vol.206,no.1,pp.321–326.

Wang,M.;Zhou,Y.;Li,Z.(1996): Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics.Physics Letters A,vol.216,no.1,pp.67–75.

Wazwaz,A.-M.(2005):Adomian decomposition method for a reliable treatment of the bratu-type equations.Applied Mathematics and Computation,vol.166,no.3,pp.652–663.

Yan,C.(1996):A simple transformation for nonlinear waves.Physics Letters A,vol.224,no.1,pp.77–84.

Zayed,E.;Gepreel,K.A.(2009): The(g′/g)-expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics.Journal of Mathematical Physics,vol.50,no.1,pp.013502.

1Faculty of Mathematical Sciences,Malayer University,Malayer,Iran.

2Department of Mathematics,University of Hafr Al-Batin,Hafr Al-Batin 31991,Saudi Arabia,Corresponding author.E-mail:yasirmath@yahoo.com

3Faculty of Mathematical Sciences and Computer,Kharazmi University,Tehran,Iran.

4Department of Mathematics,Islamic Azad University,Najafabad Branch,Najafabad,Iran.