The Influence of Gravitational Field on Generalized Thermoelasticity with Two-Temperature under Three-Phase-Lag Model

Mohamed I.A.Othman,W.M.Hasonaand Nehal T.Mansour

The Influence of Gravitational Field on Generalized Thermoelasticity with Two-Temperature under Three-Phase-Lag Model

Mohamed I.A.Othman1,2,3,W.M.Hasona2,4and Nehal T.Mansour2,5

The problem of the generalized thermoelastic medium for three different theories under the effect of a gravitational field is investigated.The Lord-Shulman,Green-Naghdi III,three-phase-lag theories are discussed with two temperature.The normal mode analysis is used to obtain the analytical expressions of the displacement components,force stress,thermodynamic temperature and conductive temperature.The numerical results are given and presented graphically,when the thermal force is applied.Comparisons are made with the results predicted by three-phase-lag model,Green-Naghdi III and Lord-Shulman theories in the presence and absence of gravity as well as two temperature.

gravity,three-phase-lag,thermoelastic,thermodynamic temperature,conductive temperature,normal-mode.

Nomenclature

λ,µ Lame’s parameter counterparts

u,wdisplacement components

ggravity

athe volume coefficient of thermal expansion

δijKronecker delta

ρ mass density

cespecific heat at constant strain

K(≥0) thermal conductivity

K∗material characteristic of the theory

Tthermodynamic temperature

T0reference temperature

φ conductive temperature

τvphase lag of thermal displacement gradient

τtphase lag of temperature gradient

τqphase lag of heat flux

b constant material"two temperature parameter"

ωijskew symmetric tensor called the rotation tensor

1 Introduction

The effect of mechanical and thermal disturbances on an elastic body is studied by the theory of thermoelasticity.This theory has two defects,it has been studied by Biot(1956).He deals with a defect of the uncoupled theory that mechanical causes have no effect on temperature.This theory predicts an in finite speed of propagation of heat waves which is a defect that it shares with the uncoupled theory.The first theory was studied by Lord and Shulman(1967),who formulated the generalized thermoelasticity theory involving one thermal relaxation time.The second theory was discussed by Green-Lindsay(1972).They introduced two different relaxation times in the entropy expression and stress-strain relations.The third generalization of the coupled theory of thermoelasticity introduced by Green and Naghdi(1993)whose developed different theories labeled type I,type II,and type III.The Green-Naghdi(G-N)theory of type I in the linearized theory is equivalent to the classical coupled thermoelasticity theory,the(G-N)theory of type II does not admit energy dissipation,and the third(G-N)theory of type III admits dissipation of energy and the heat flux is a combination of type I and type II.The fourth generalization of the coupled theory of thermoelasticity is developed by Tzau(1995)and Chandrasekhariah(1998)and is referred to the dual-phase-lag thermoelasticity.Abbas and Othman(2012)have studied the generalized thermoelsticity of thermal shock problem in an isotropic hollow cylinder and temperature dependent elastic moduli.Raychoudhuri(2007)has recently introduced the three-phase-lag,heat conduction equation in which the Fourier law of heat conduction is replaced by an approximation to a modi fication of the Fourier law with the introduction of three different phase-lag for the heat flux vector,the temperature gradient and the thermal displacement gradient.The stability of the three-phase-lag,the heat conduction equation is discussed by Quintanilla and Racke(2008).Reflection and transmission of waves from the imperfect boundary between two heat conducting micropolar thermoelastic solids by Marin(2014a).Weak solutions in elasticity of dipolar bodies with stretch were studied by Marin(2013).On temporal behav-ior of solutions in thermoelasticity of porous micropolar bodies by Marin(2014b).The effect of initial stress on generalized thermoelastic medium with three-phaselag model under temperature dependent properties has studied by Othman et al.(2014a).Subsequently Kar and Kanoria(2009)have employed this theory of thermoelasticity with three-phase-lag to discuss a problem of thermoelastic interactions on functional graded orthotropic hollow sphere under thermal shock.

In the classical theory of elasticity,the gravity effect is generally neglected.Generalized thermoelastic medium with temperature-dependent properties for different theories under the effect of gravity field has studied by Othman et al.(2013a).The effect of gravity in the problem of propagation of waves in solids,in particular on an elastic globe,was first studied by Bromwich(1898).The influence of the gravitational field and rotation on a generalized thermoelastic medium using a dual-phase-lag model has studied by Othman et al.(2013b).Subsequently,an investigation of the influence of the gravitational field and rotation on thermoelastic solid with voids under Green-Naghdi theory was considered by Othman et al.(2013c).The effect of gravity on the surface waves,on the propagation of waves in an elastic layer has been studied by De and Sengupta(1974 and 1978).The effect of rotation on micropolar generalized thermoelasticity with two temperature using a dual-phase-lag model has studied by Othman et al.(2014b).Generalized thermoelsticity of thermal shock problem in a non-homo-geneous isotropic hollow cylinder with energy dissipation studied by Othman and Abbas(2012).

The two temperature theory of thermoelasticity was introduced by Gurtin and Williams(1967),Chen and Gurtin(1968),and Chen et al.(1968),in which the classical Clausius-Duhem inequality was replaced by another one depending on two temperature;the conductive temperature and the thermodynamic temperature,the first is due to the thermal processes,and the second is due to the mechanical processes inherent between the particles and the layers of elastic material,this theory was also investigated by Iesan(1970).The two-temperature model was underrated and unnoticed for many years thereafter.Only in the last decade has the theory been noticed,developed in many works,and find its applications,mainly in the problems in which the discontinuities of stresses have no physical interpretations.Among the authors who contribute to develop this theory,Quintanilla(2004)studied existence,structural stability,convergence and spatial behavior of this theory.Youssef (2006) introduced the generalized Fourier’s law to the field equations of the two-temperature theory of thermoelasticity and proved the uniqueness of the solution for homogeneous isotropic material,Puri and Jordan(2006)studied the propagation of harmonic plane waves.Recently,Magaña and Quintanilla(2009)have studied the uniqueness and growth solutions for the model proposed by Youssef(2006).

The present paper is concerned with the investigations related to the effect of gravity with two temperature on a generalized thermoelastic medium based on threephase-lag model by applying the normal mode analysis.Also,the effect of gravity and two-temperature on the physical quantities are discussed numerically and illustrated graphically.

2 Formulation of the problem and basic equations

We consider a homogeneous thermoelastic half-space with two-temperature under the influence of gravity.All the considered quantities are functions of the time variabletand of the coordinatesxandzWe consider the normal source acting on the plane surface of generalized thermoelastic half-space under the influence of gravity.The system of governing equations of a linear thermoelasticity with gravity and without body forces consists of:

The stress-strain relation written as:

The equation of motion in the absence of body force

The equation of heat conduction under three phase lag model

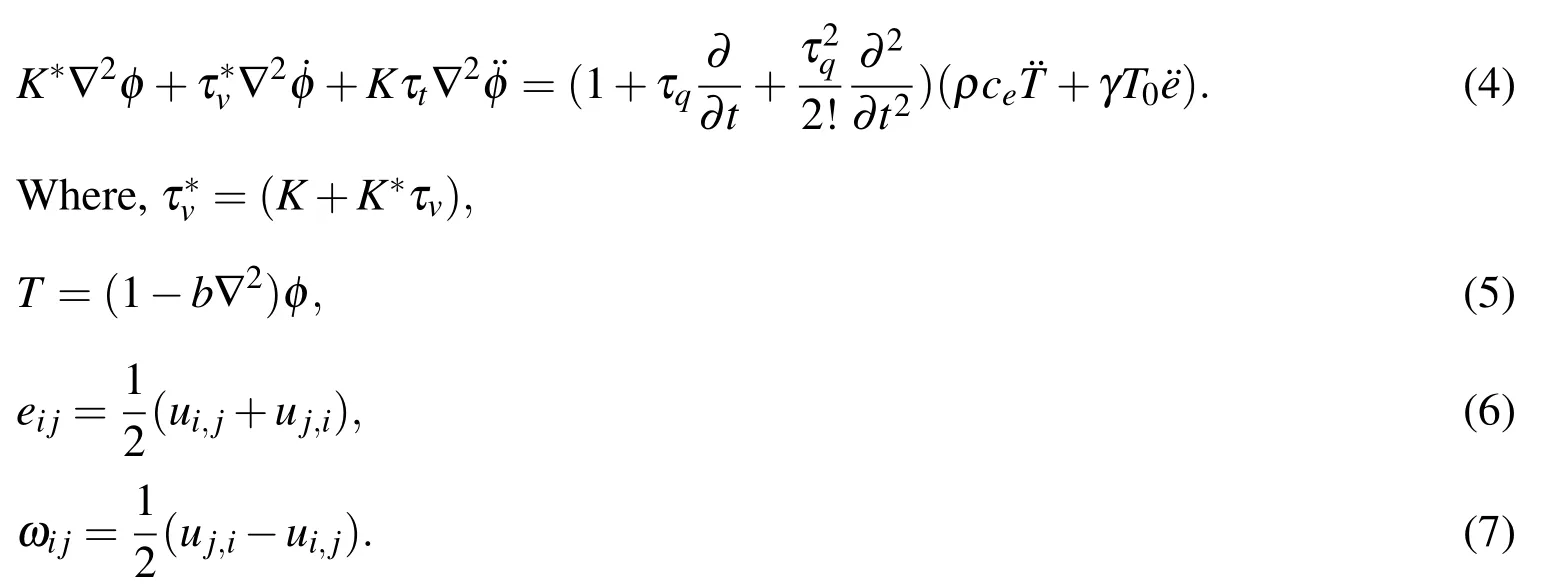
For a two dimensional problem inxz-plane,Eqs.(2)-(4)can be written as:

For the purpose of numerical evaluation,we introduce dimensions variables

Using the above dimensions quantities,Eqs.(8)-(10)become

We define displacement potentialsqand ψ which relate to displacement componentsuandwas,

Using Eq.(14)in Eqs.(11)-(13),we obtain:

3 Normal mode analysis

The solution of the considered physical variable can be decomposed in terms of normal modes as the following form

Where,ω is the complex time constant andais the wave number inx-direction.Using(18)in Eqs.(15)-(17),we obtain

The solution of Eq.(22)has the form

Where,Mn(n=1,2,3)are some constants,are the roots of the characteristic equation of Eq.(22).

Dimensionless variables of the stress components yields the following,

Using Eq.(14)and Eqs.(23)-(26)in(27)-(29)

Where,

4 Boundary conditions

The boundary conditions on the plane surfacez=0 are:

Using Eqs.(32),(34)and(35)in boundary conditions(36),we get three equations in three constantsMn(n=1,2,3)as:

Solving Eqs.(37)-(39)the constantsMn(n=1,2,3)are defined as follows:

Where,

5 Numerical results

To study the effect of gravity and two-temperature,we now present some numerical results.For this purpose,copper is taken as the thermoelastic material for which we take the following values of the different physical constants.

The numerical technique,outlined above,was used for the distribution of the real part of the temperatureT,the displacement componentsu,wand the stress components σxx,σzz,σxzfor the problem.There are three lines expressing theories are,the"solid line"expresses the 3PHL theory,the"cross line"expresses the L-S theory,and the"dashed line"expresses the G-N III theory.Figs.1(a,b)-6(a,b)show the distribution of the physical quantities based on L-S,G-N III and 3PHL in the case ofg=0,9.8 respectively.Fig.1(a,b)depict that the displacement componentuincreases with the increase of gravity in the three theories.In the absence and presence of gravity(i.e.g=0,9.8),ubegins to increase then smooth decreases and takes the form of wave and try to return to zero.Fig.2(a,b)exhibit that the displacement componentwincreases with the decrease of gravity,and takes the form of a wave until it develops to zero,that’s mean that the displacementwis inversely proportional with gravity.Fig.3(a,b)demonstrate that the behavior of temperatureTdecreases forg=0,9.8 and takes the form of a wave until it develop to zero.Fig.4(a,b)show that the stress component σxzincreases with the increase of gravitygin L-S,and decreases with the decrease of the gravity in G-N III and 3PHL and takes the form of the wave until it develop to zero.Fig.5(a,b)depict that the stress component σxxbegins from the value zero and satis fies the boundary condition atz=0 in the three theories.The stress component σxxdecreases with the increase of gravity in L-S and 3PHL,and decreases during the period 0≤z≤1,then increasing and takes the form of the wave until it develop to zero atg=9.8 in G-N III,while increases in the period 0≤z≤1,then decreasing and takes the form of the wave until it develop to zero atg=0 in G-N III.Fig.6(a,b)explain that the stress component σzzdecreases in the case ofg=0,9.8 and decays to zero.

Figs.7(a,b)-12(a,b)exhibit the distribution of the physical quantities based on L-S,G-N III and 3PHL in the case ofb=0,0.1.Fig.7(a,b)show that the displacement componentuincreases with the increase ofbin G-N III and L-S theories,while,it decreases with the increase ofbin 3PHL theory,and try to return to zero at infinity in three theories.Fig.8(a,b)demonstrate that the displacement componentwincreases atb=0.1,in three theories,in the range 0≤z≤1,while decreases atb=0,in 3PHL theory,then,increases atb=0,in the range 0≤z≤0.5,in G-N III and L-S theories,and takes the form of the wave until it develop to zero in three theories.Fig.9(a,b)explain that the temperature satis fies the boundary conditions atz=0 and decreases,in the three theories to a minimum value in the range 0≤z≤1,atb=0.1,while,increases forz≥0.75,atb=0,then,it decays to zero in the two cases.Fig.10(a,b)explain that the stress component σxzdecreases atb=0.1,in the range 0≤z≤0.5 of the three theories,while decreases in the range 0≤z≤0.5 forb=0 in the two theories L-S and 3PHL,but it increases forb=0 in G-N III,and takes the form of the wave until it develop to zero in L-S and G-N III and 3PHL theories.Fig.11(a,b)show that the stress component σxxsatis fies the boundary condition and decreases to a minimum value in the range 0≤z≤1,and increases in the range 1≤z≤2,but,decays to zero in the three theories,forb=0.1,while,increases in the range 0≤z≤0.5 forb=0 in 3PHL and G-N III theories and decays to zero,then,decreases in the range 0≤z≤0.5 forb=0,and increases in the range 0.5≤z≤1 forb=0 until it develop to zero in L-S theory.Fig.12(a,b)show that the stress component σzzdecreases forb=0.1,in the three theories,and it decreases forb=0,in L-S and G-N III,but increases forb=0,in 3PHL then,decays to zero.

Figure 1:Distribution of displacement component u in the presence and absence of g.

Figure 2:Distribution of displacement component w in the presence and absence of g.

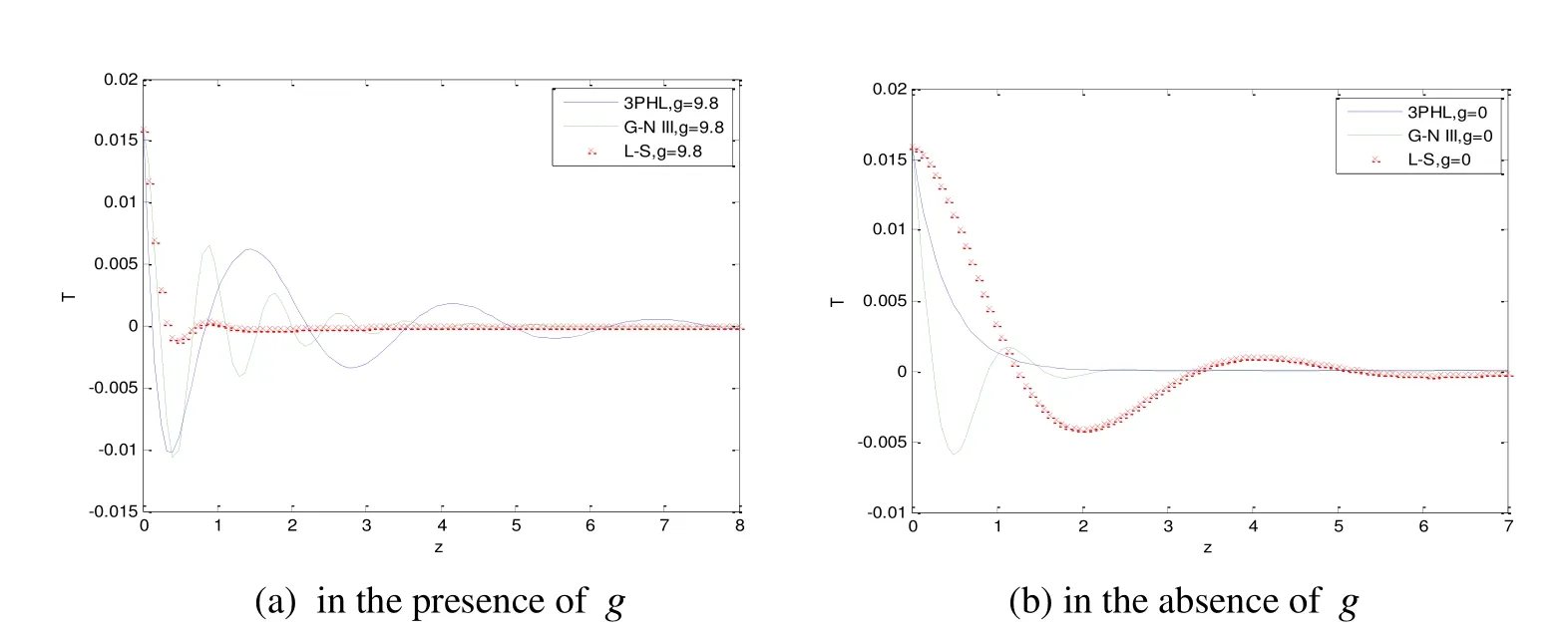
Figure 3:Distribution of the temperature T in the presence and absence of g.

Figure 5:Distribution of the stress component σxxin the presence and absence of g.

Figure 6:Distribution of the stress component σzzin the presence and absence of g.

Figure 7:Distribution of displacement component u in the presence and absence of b.

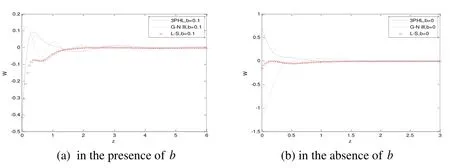
Figure 8:Distribution of displacement component w in the presence and absence of b.

Figure 9:Distribution of the temperature T in the presence and absence of b.

Figure 10:Distribution of the stress component σxzin the presence and absence of b.

Figure 11:Distribution of the stress component σxxin the presence and absence of b.

Figure 12:Distribution of the stress component σzzin the presence and absence of b.

6 Conclusion

By comparing the figures obtained under the three theories,important phenomena are observed:

1.Analytical solutions based upon normal mode analysis of the thermoelastic problem in solids have been developed.

2.The method that is used in the present article is applicable to a wide range of problems in hydrodynamics and thermoelasticity.

3.There are significant differences in the field quantities under GN-III,3PHL and L-S theories.

4.The presence of the gravitational field and two-temperature plays a significant role on all physical quantities.

5.The comparison of the three theories of thermoelasticity,Lord-Shulman theory,three-phase-lag model and Green-Naghdi III is carried out.

6.The value of all the physical quantities converges to zero,and all the functions are continuous.

Abbas,I.A.,Othman,M.I.A.(2012):Generalized thermoelsticity of thermal shock problem in an isotropic hollow cylinder and temperature dependent elastic moduli.Chinese Physics B,vol.21,no.1,pp.14601-14606.

Biot,M.A.(1956):Thermoelasticity and irreversible thermodynamics.Journal of Applied Physics,vol.7,pp.240-253.

Bromwich,T.J.(1898):On the influence of gravity on elastic waves and in particular on the vibrations of an elastic globe.The Proceedings of the London Mathematical Society,vol.30,pp.98-120.

Chandrasekharaiah,D.S.(1998):Hyperbolic thermoelasticity:A review of recent literature.Applied Mechanics Reviews,vol.51,pp.705-729.

Chen,P.J.;Gurtin,M.E.(1968):On a theory of heat conduction involving two temperatures.Journal of Applied Mathematics and Physics,vol.19,pp.614-627.

Chen,P.J.;Gurtin,M.E.;Williams,W.O.(1968):A note on non-simple heat conduction.Journal of Applied Mathematics and Physics,vol.19,pp.969-970.

De,S.N.;Sengurta,P.R.(1974):In fluence of gravity on wave propagation in an elastic layer.The Journal of the Acoustical Society of America,vol.55,pp.919-921.

De,S.N.;Sengurta,P.R.(1976):Surface waves under the influence of gravity.Gerlands Beitr Geophys(Leipzig),vol.85,pp.311-318.

Green,A.E.;Lindsay,K.A.(1972):Thermoelasticity.Journal of Elasticity,vol.2,pp.1-7.

Green,A.E.;Naghdi,P.M.(1993):Thermoelasticity without energy dissipation.Journal of Elasticity,vol.31,pp.189-209.

Gurtin,M.E.;Williams,W.O.(1967):An axiom foundation for continuum thermo-dynamics.Archive for Rational Mechanics and Analysis,vol.26,pp.83-117.

Ie¸san,D.(1970):On the linear coupled thermoelasticity with two-temperatures.Journal of Applied Mathematics and Physics,vol.21,pp.583-591.

Kar,A.;Kanoria,M.(2009):Generalized thermoelastic functionally graded orthotropic hollow sphere under thermal shock with three-phase-lag effect.EuropeanJournal of Mechanics-A/Solids,vol.28,pp.757-767.

Lord,H.W.;Shulman,Y.A.(1967):Generalized dynamical theory of thermoelasticity.Journal of the Mechanics and Physics of Solids,vol.15,pp.299-309.

Magaña,A.;Quintanilla,R.(2009):Uniqueness and growth of solutions in two temperature generalized thermoelastic theories.Mathematics and Mechanics of Solids,vol.14,pp.622-634.

Marin,M.(2013):Weak solutions in elasticity of dipolar bodies with stretch.Carpathian Journal of Math,vol.29,no.1,pp.33-40.

Marin,M.(2014a):Reflection and transmission of waves from imperfect boundary between two heat conducting micropolar thermoelastic solids.Annales Universitatis Scientiarum Ovidius,Mathematics Series,vol.22,no.2,pp.151-175.

Marin,M.(2014b):On temporal behaviour of solutions in thermoelasticity of porous micropolar bodies.Annales Universitatis Scientiarum Ovidius,Mathematics Series,vol.22,no.1,pp.169-188.

Othman,M.I.A.;Abbas,I.A.(2012):Generalized thermoelsticity of thermal shock problem in a non-homogeneous isotropic hollow cylinder with energy dissipation.International Journal of Thermophysics,vol.33,no.5,pp.913-923.

Othman,M.I.A.;Elmaklizi,Y.D.;Said,S.M.(2013a):Generalized thermoelastic medium with temperature-dependent properties for different theories under the effect of gravity field.International Journal of Thermophysics,vol.34,pp.521-537.

Othman,M.I.A.;Hasona,W.M.;Eraki,E.M.(2013b):In fluence of gravity field and rotation on a generalized thermoelastic medium using a dual-phase-lag model.Journal of Thermoelasticity,vol.1,pp.2328-2401.

Othman,M.I.A.;Zidan,M.E.M.;Hilal,M.I.M.(2013c):The influence of gravitational field and rotation on thermoelastic solid with voids under Green-Naghdi theory.Journal of Physics,vol.2,pp.22-34.

Othman,M.I.A.;Hasona,W.M.;Abd-Elaziz,E.M.(2014a):The effect of initial stress on generalized thermoelastic medium with three-phase-lag model under temperature dependent properties.Canadian Journal of Physics,vol.92,pp.448-457.

Othman,M.I.A.;Hasona,W.M.;Abd-Elaziz,E.M.(2014b):Effect of rotation on micropolar generalized thermoelasticity with two temperature using a dualphase-lag model.Canadian Journal of Physics,vol.92,pp.149-158.

Puri,P.;Jordan,P.M.(2006):On the propagation of harmonic plane waves under the two-temperature theory.International Journal of Engineering Science,vol.44,pp.1113-1126.

Quintanilla,R.(2004):On existence,structural stability,convergence and spatial behavior in thermoelasticity with two-temperatures.Acta Mechanica,vol.168,pp.61-73.

Quintanilla,R.;Racke,R.(2008):A note on stability in three-phase-lag heat conduction.International Journal of Heat and Mass Transfer,vol.51,pp.24-29.

Roy Choudhuri,S.K.(2007):On thermoelastic three phase lag model.Journal of Thermal Stresses,vol.30,pp.231-238.

Tzou,D.Y.(1995):A uni fied field approach for heat conduction from macro to microscales.The ASME Journal of Heat Transfer,vol.117,pp.8-16

Youssef,H.M.(2006):Theory of two-temperature generalized thermoelasticity.IMA,Journal of Applied Mathematics,vol.71,pp.383-390.

1Department of Mathematics,Faculty of Science,Taif University 888,Saudi Arabia.

2Department of Mathematics,Faculty of Science,Zagazig University,P.O.Box 44519,Zagazig,Egypt.

3E-mail:m_i_a_othman@yahoo.com

4E-mail:wahedhasona@yahoo.com

5E-mail:nehal.tarek23@yahoo.com