Analytical Solution of Thermo-elastic Stresses and Deformation of Functionally Graded Rotating Hollow Discs with Radially Varying Thermo-mechanical Properties under Internal Pressure

M.R.Akbariand J.Ghanbari,2

Analytical Solution of Thermo-elastic Stresses and Deformation of Functionally Graded Rotating Hollow Discs with Radially Varying Thermo-mechanical Properties under Internal Pressure

M.R.Akbari1and J.Ghanbari1,2

Exact analytical solution for functionally graded hollow discs under internal pressure,thermal load and rotation are provided in this paper.Material properties of discs,i.e.elastic modulus,density and thermal expansion coefficient are assumed to vary in radial direction.Two power functions are assumed for property dependency to study various types of functional grading of materials in the discs.Assuming small deformations,a differential equation is obtained and solved for the Airy stress function.The effects of various grading functions on the stress and deformation distribution are studied and an optimum value for the power is obtained.

Functionally graded materials, Thermo-elastic solution, Rotating discs.

1 Introduction

In functionally graded materials(FGMs),usually two different materials,e.g.a metal and a ceramic,are distributed throughout the body according to a smooth distribution function.The material properties are thus functions of position,gradually changing from one specific material,namely a metal to another,a ceramic.FGMs for their excellent mechanical properties such as high strength impact,creep,erosion and thermal tolerance are highly considered by researchers in extreme loading environments[Suresh and Mortensen(1998)].The metal part of an FGM tolerates mechanical stresses while the ceramic part is a good thermally stable part resisting high erosive conditions[Reddy et al.(1999)].Because of these properties,FGMs are an ideal choice for applications with high temperature and severe temperature gradients.By controlling material distribution in the required dimension,even thin-walled structures are achieved[Niino and Maeda(1990)].

For better understanding the mechanical behavior of FGMs,various methods are employed by researchers to achieve an optimal design for the specific application.Oral and Anlas(2005)have studied mechanical behavior of non-homogeneous cylindrical bodies assuming a power function dependency of mechanical properties on the radius.Horgan and Chan(1999)considered hollow cylinders under internal pressure,also assuming a power function dependency of the mechanical properties on the radius of the cylinder.Nadeau and Ferrari(1999)studied thermal stresses in a non-homogeneous plate with through the thickness variation of the mechanical properties.A closed-form solution for spherical and cylindrical pressure vessels of FGMs is developed by Tutuncu and Ozturk(2001).Liu et al.(2013)developed an analytical methodology using the averaging technique of composites to describe the thermo-elastic and thermo-elastoplastic behavior of a triple-layered FGM system subjected to thermal loadings.Xie and Chi(2014)studied dynamic response sensitivity of a simply supported functionally graded magneto-electroelastic plates by combining analytical method with finite element method.In their work,the FGM parameters are assumed to obey exponential law in the thickness direction Also an exact three-dimensional elastic model for the free vibration analysis of functionally graded sandwich simply-supported plates and shells is proposed by Brischetto(2013).

Rotating discs are common in internal combustion engines,centrifugal compressors,turbine rotors and flywheels and operate in harsh thermal conditions which require an appropriate material to withstand applied thermal and mechanical loads.In recent years,FGMs are considered as a good choice of material for these discs and various studies have been conducted by researches for this purpose.Durodola and Attia(2000)studied hollow and solid FGM discs reinforced by fibers and employed the finite element method for their deformation and stress analysis.Bayat et al.(2009)studied bending of rotating FGM discs using first order shear deformation theory and obtained semi-analytical solution for small deformation case.Kadkhodayan and Golmakani(2011)used von Karman equations for large deformation case and analyzed bending of rotating hollow and solid FGM discs.Asghari and Ghafoori(2010)employed a semi-analytical 3D solution to better study the stress on thick rotating discs.Hosseini Kordkheili and Naghdabadi(2007)presented a semi-analytical thermo-elastic solution for constant thickness hollow and solid rotating FGM discs and compared the results with those of the finite element analysis.Bayat et al.(2009)presented a thermo-elastic solution for variable thickness FGM discs.Ghorbanpour et al.(2010)studied variable thickness discs using a magneto-thermo-elastic analysis and obtained a semi-analytical solution.

In this paper,we present an exact closed-form solution for thermo-elastic analysis of hollow rotating FGM discs under internal presser and temperature gradient throughout the radial direction of the disc.As mentioned earlier,in previous works usually a semi-analytical solution is obtained for discs with radial variation in material properties.In this work,we employed a power function dependency of properties with respect to radial distance instead of the volume fraction of materials.Both internal and external radii are considered as reference position for the grading function and by choosing different values for the power,an optimal value has been obtained for near uniform stress distribution throughout the radial axis of the disc.

2 Problem formulation

2.1 Grading function

A power dependency between the properties and radial distance is used in this paper for the FGM disc.Both inner and outer radius are considered as the reference position.For disc A,the inner radius is considered as the reference position and the material properties depend on radial position as,

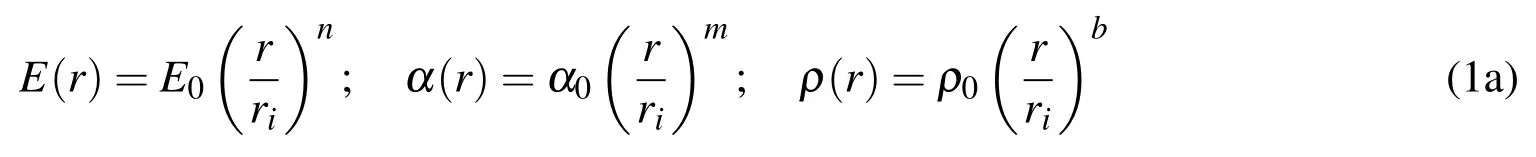
And for disc B,the outer radius is chosen as the reference position,

whereriandroare inner and outer radii of the disc,respectively,andn,m,andbare arbitrary powers related to the grading of the materials.Note that for these powers equal to zero,isotropic material properties will be obtained(see Fig.1)

2.2 Temperature gradient

A temperature gradient is assumed in the radial direction of the rotating disc which is assumed to vary according to,

As can be seen,the temperature on the inner radius is kept asT0and 0 on the outer radius.

2.3 Governing equations

The equilibrium equation in the radial direction for an FGM disc rotating with constant angular velocity of ω assuming a plane stress state can be expressed as,

Figure 1:Schematic of an FG rotating disc subjected to thermal loading.

Since geometry,loadings and material properties have rotational symmetry with respect to the axis of rotation of the disc,both radial and circumferential stresses are just functions ofrand do not depend on θ.Also,the shear stress τrθis identically zero.

Using the general thermo-elastic Hooke’s law,the strain components are,

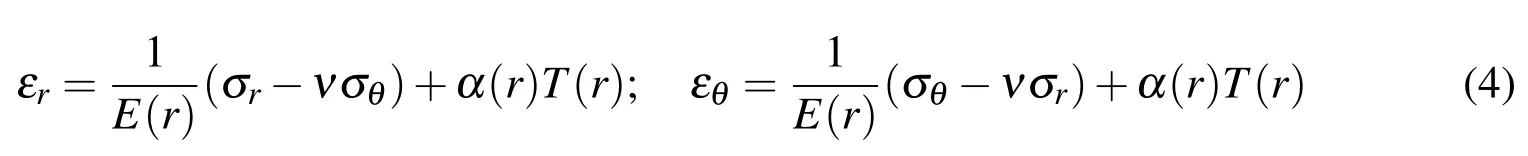
whereT(r)is the temperature given in Eq.2.Note that the Poisson’s ratio is assumed to be constant throughout the disc.

To solve the equilibrium equation in Eq.3,we use the Airy stress function,F,with stress components de fined as,

In axisymmetric plane stress state,the strain-displacement relations are as follows,

whereuis the displacement component along the radial direction.Combining the relations in Eq.6,we have,

Substituting Eq.5 into Eq.4 and the results in Eq.7,we arrive at,

Eq.8 is a non-homogeneous ordinary differential equation and its solution involves a general homogeneous solution and a particular non-homogeneous one.To obtain the solution to the homogeneous equation,we use a substitution of variables like,

whereC1andC2are constants which will be obtained from boundary conditions,and

The particular solution may be obtained as

whereG,H,andJare constants.For disc A,these constants are obtained as,

For disc B,similar expressions are obtained as follows,

Now,the solution to the Eq. 8 is the sum of the homogeneous and non-homogeneous solutions,Eqs.9 and 11,

Using Eq.5,the stress components are derived.For disc A,

Similarly,for disc B,

Using Eq.4,the strain components can be obtained.For disc A,

And for disc B,

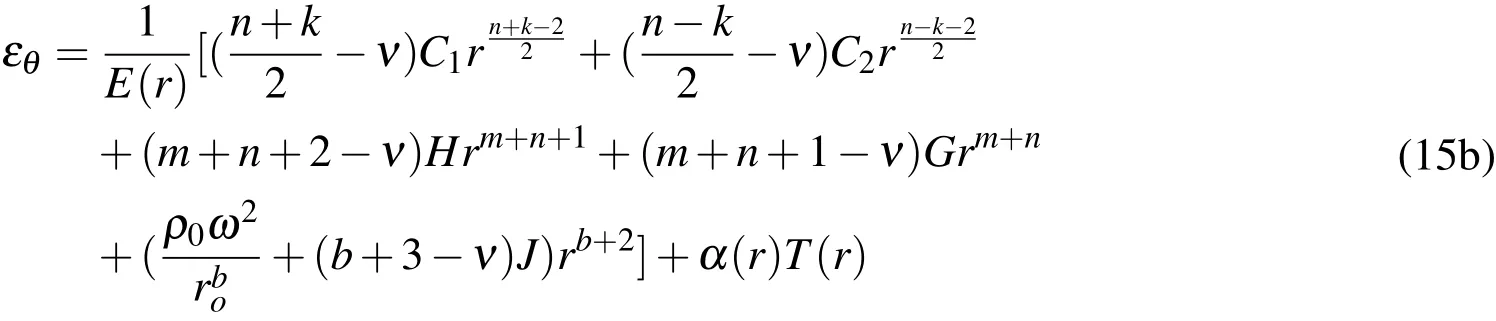
Substituting Eqs.15-a and 15-b into Eq.6,the radial displacement is obtained as,

For disc A;and for disc B as follows,

2.4 Boundary conditions

To fully determine displacements and the stress components of the discs,we need to apply the boundary conditions on the inner and outer radii of the discs.As we mentioned earlier,we assumed that the discs are under internal pressure and the outer surface is traction-free.So,we have

Applying these conditions,constantsC1andC2are determined,

3 Results and discussions

For better illustration and interpretation of the results,we first define dimensionless parameters for material properties,stress,and strains as follows,

To plot the results,we have used the following numerical values for the geometry and mechanical properties of the discs,

Figs.2.a and 2.b show the dimensionless Young’s modulus of disc A and B for different values of the powernwith respect to radial distance.Both positive and negative values fornhave been considered in the analysis.The variation of thermal expansion coefficient α is shown in Figs 2.c and 2.d for discs A and B,respectively.Similar behavior for the density of the discs can be seen in Figs 2.e and 2.f.

By choosing different relations for describing the dependency of properties on the radial distance,we are able to tune the power values in these relations to match those of experimental data or more accurate modeling of merely the mechanical properties of FGM discs,while maintaining the solvability of the derived equations and yielding a closed form solution for the problem.

The results for stress and strain components are illustrated on Figs 3 and 4 Figs 3.a and 3.b show the variation of radial stress through the radial distance of both discs for various values ofn.Disc A shows more sensitivity to the value ofnthan disc B.For decreasing values ofn,the stress distribution on the disc tends to be uniform,especially for disc A.This is also the case for the circumferential stress component shown in Figs 3.c and 3.d.Again,disc A is more sensitive to the value of powern.Forn=1,2,minimum values for the radial stress component occur at the middle of the discs,while forn=0,-1,-2,internal radius has the minimum value for the radial stress,which is equal to the applied internal pressure.Disc B does not show this behavior and the minimum value of the radial stress is always occur on the internal radius of the disc corresponding to the applied pressure.

Figure 2:Material property distribution on the discs:(a)and(b)elastic modulus on discs A and B;(c)and(d)thermal expansion coefficient on discs A and B;(e)and(f)density on discs A and B,respectively with respect to various values for the power in the grading function.

Figure 3:Stress distribution in the radial direction:(a)and(b)radial stress component for discs A and B;(c)and(d)circumferential stress component for discs A and B,respectively.

Considering the circumferential stress component,in disc A,there is a smoother variation along the radius forn=-1,-2 compared to other values ofn.The maximum value of the stress always occur on the outer radius,except for the case ofn=-2 for which internal radius of the disc has the maximum value of the stress.Disc B always has the maximum stress on its outer radius.For decreasing value ofn,stress gradient decreases along the radial direction.

Contrary to the stress components,the strain components tend to decrease with respect to radial distance,as shown in Fig.4.For increasing values ofn,circumferential strain values decrease throughout disc A,but increase in disc B.On the other hand,the radial strain component increases for disc A and decreases for disc B for increasing values ofn.Fig.5 shows the variation of radial displacement for discs

Figure 4:Strain distribution in the radial direction:(a)and(b)radial strain component for discs A and B;(c)and(d)circumferential strain component for discs A and B,respectively.

A and B for various values ofn.For increasing values ofn,radial displacement decreases for disc A,while increases for disc B.

The effects of angular velocity on the stress and deformation components are depicted in Fig.6 for disc A and for the casen=2.For increasing angular velocity,both stress components and radial displacement increase throughout the disc.

For better understanding the effects of temperature gradient on the stresses and displacement of the disc A,various cases are illustrated in Fig.7.For increasing temperature on the inner radius,the radial stress component shows more intensive gradient in the radial direction.The circumferential stress component decreases on the inner radius and increases on the outer radius for increasing temperature gradient.The radial displacement increases for increasing temperature gradient.Note that for Fig 7,the dimensionless parameters are

Figure 5:Radial displacement component distribution in disc A(a),and in disc B(b).

Figure 6:The effects of angular velocity on radial stress(a),and circumferential stress(b)components and radial displacement(c)for disc A.

Figure 7:The effects of temperature gradient on radial(a),and circumferential stress distribution(b)and radial displacement(c)for disc A.

4 Conclusion

An analytical exact solution for functionally graded rotating discs under thermo mechanical loads is obtained in this paper.The discs are assumed to have constant thickness and the grading is on the radial direction.A power grading function is chosen so that a closed form elasticity solution can be obtained.Since the grading is on the radial direction,with the chosen function,mechanical properties on either inner or outer radius are set exactly and on the other side is tuned by the power value.To study the effect of this choice,two discs are considered.In disc A,inner radius is the base for mechanical property variation and in disc B,outer radius is the base.

Stress and strain component variations throughout the radius of the discs are stud-ied.The variation ofnchanges the stress components behavior,from ascending to descending in some cases,while retain the general behavior for strain components.If an optimal design based on stress distribution is desired,it is possible to determine the proper grading of the base materials throughout the grading direction using the proposed method in this paper.

Asghari,M.;Ghafoori,E.(2010):A three-dimensional elasticity solution for functionally graded rotating disks.J.Compos.Struct.,vol.92,pp.1092-1099.

Bayat,M.;Sahari,B.B.;Saleem,M.;Hamouda,A.M.S;Reddy,J.N.(2009):Thermo elastic analysis of functionally graded rotating disks with temperature dependent material properties:uniform and variable thickness.Int.J.Mech.Mater.Des.,vol.5,pp.263-279.

Bayat,M.;Sahari,B.B.;Saleem,M.;Aidy,A.;Wong,S.V.(2009):Bending analysis of a functionally graded rotating disk based on the first order shear deformation theory.J.Appl.Math.Model.,vol.33,pp.4215-4230.

Brischetto,S.(2013):Exact elasticity solution for natural frequencies of functionally graded simply-supported structures.CMES:Computer Modeling in Engineering&Sciences,vol.95,no.5,pp.391-430.

Durodola,J.F.;Attia,O.(2000):Deformation and stresses in FG rotating disks.J.Compos.Sci.Technol.,vol.60,pp.987-995.

Golmakani,M.E.;Kadkhodayan,M.(2011):Nonlinear bending analysis of annular FGM plates using higher-order shear deformation plate theories.J.Compos.Struct.,vol.93,pp.973-982.

Ghorbanpour Arani,A.;Loghman,A.;Shajari,A.R.;Amir,S. (2010):Semianalytical solution of magneto-thermo-elastic stresses for functionally graded variable thickness rotating disks.J.Mech.Sci.Technol.,vol.24,no.10,pp.2107-2117.

Horgan,C.O.;Chan,A.M.(1999):The pressurized hollow cylinder or disk problem for functionally graded isotropic linearly elastic materials.J.Elasticity,vol.55,pp.43-59.

Kordkheili,S.A.H.;Naghdabadi,R.(2007):Thermoelastic analysis of a functionally graded rotating disk.J.Compos.Struct.,vol.79,pp.508-516.

Liu,B.;Dui,G.;Xie,B.;Xin,L.;Xue,L.(2013):A theoretical analysis on elastic and elastoplastic stress solutions for functionally graded materials using averaging technique of composites.CMC:Computers,Materials&Continua,vol.34,no.1,pp.83-94.

Nadeau,J.C.;Ferrari,M.(1999):Microstructural optimization of a functionally graded transversely isotropic layer.J.Mech.Mater.,vol.31,pp.637-651.

Niino,M.;Maeda,S.(1990):Recent development status of functionally gradient materials.J.Thin Wall.Struct.,vol.30,pp.699-703.

Oral,A.;Anlas,G.(2005):Effects of radially varying moduli on stress distribution of nonhomogeneous anisotropic cylindrical bodies.Int.J.Solids Struct.,vol.42,pp.5568-5588.

Reddy,J.N.;Wang,C.M.;Kitipornchai,S.(1999):Axisymmetric bending of functionally graded circular and annular plates.Eur.J.Mech.A/Solids,vol.18,pp.185-199.

Suresh,S.;Mortensen,A.(1998):Fundamentals of functionally graded material.Processing and thermo mechanical behavior of graded metals and metal-ceramic composites.IOM Communications LTD,London,UK.

Tutuncu,N.;Ozturk,M.(2001):Exact solutions for stresses in functionally graded pressure vessels.J.Compos.Part B-Eng.,vol.32,pp.683-686.

Xie,G.Q.;Chi,M.X.(2014):Sensitivity of dynamic response of a simply supported functionally graded magneto-electro-elastic plate to its elastic parameters.CMC:Computers,Materials&Continua,vol.44,no.2,pp.123-140.

1Department of Mechanical Engineering,Qom University of Technology,37195-1519,Qom,Iran.

2Corresponding author.E-mail:ghanbari@qut.ac.ir