组合预测理论在云南电力需求预测中的应用

张劭辉

(云南电网有限责任公司,昆明 650011)

组合预测理论在云南电力需求预测中的应用

张劭辉

(云南电网有限责任公司,昆明 650011)

以云南地区电力需求发展为研究对象,分析了云南地区经济、人口的发展特性,分别构建了云南地区电力需求多元线性回归预测模型以及灰色预测模型,并提出了基于组合预测理论进行修正改进的预测思想。

云南地区；电力需求；组合预测；多元线性回归；灰色预测

1 组合预测模型构建

1.1 多元线性回归模型基本原理

回归预测法即通过对变量的观测数据进行统计分析,确定变量及其影响因素之间的相关关系,从而实现对变量进行预测的目的。

回归预测包括线性回归和非线性回归,其中线性回归又包括一元线性回归和多元线性回归。一元线性回归模型表示为

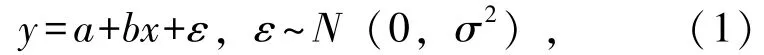
其中x表示自变量,y表示因变量,ε表示随机误差,它与回归系数a,b均是不依赖于x的未知参数,通过估计参数a,b的值从而得到y对x的线性回归方程

多元线性回归分析原理与一元线性回归基本相同,但计算形式较复杂,为研究随机变量y与多个可控变量xp之间的线性相关关系,其中p＞1。非线性回归则是研究自变量与因变量之间为非线性关系的情况,也是实际问题中多见的表现形式,但通常都可以通过变量代换转化为线性关系进行处理,如幂函数关系、指数函数关系等。在解决实际的预测问题时,需要检验回归方程是否具有实用价值。

1.2 灰色预测模型基本原理

灰色预测法就是把随机量 (如负荷)当作在一定范围内变化的灰色量,将无规律的历史数据列经过AGO(累加生成)或IAGO(累减生成)等方法,使其变为具有一定规律的数据列,对生成后的数列建立微分方程模型。GM(1,1)模型是最常用的一种灰色模型,它是由一个只包含单变量 (如负荷)的一阶微分方程构成的模型,最终的灰色预测模型就是通过GM(1,1)模型的时间响应函数模型经过累减还原或累加还原得到的。GM(1,n)模型则表示对n个变量用一阶微分方程建立的灰色模型,用于建立负荷和若干影响变量之间关系的预测模型。

灰色预测解决了以往统计预测的配曲线问题,目标是通过一个模型解决所有预测问题,它的优点在于要求负荷数据少、不考虑分布规律及变化趋势、短期预测精度高、易于检验且噪音干扰小。缺点就在于当数据离散程度比较大时,预测精度较差；不适合长期后推若干年的预测,因为随着时间的推移,未来的扰动因素不断进入,导致预测周期越长,灰度越大,预测值的实际意义越小。

1.3 组合预测模型基本思路

由于多元线性回归模型更多的考虑的影响负荷变化的相关因素,而灰色预测模型能够较为深入的挖掘负荷数据序列本身的变化规律,两种方法具有各自的特色,同时存在着一定的不足。因此,本文结合优选组合预测模型基本思想中的组合赋权理论,依据方差—协方差方法来确定不同预测方法的权重,然后进行加权求和计算,得到新的预测模型。其优点为既可以涵盖多元线性回归预测模型考虑经济、人口等因素的特点,也可以获取灰色预测模型充分挖掘电力需求数据序列自身变化规律的优势。两种预测模型权重大小的确定主要依据各自预测结论数据序列的误差分布情况,组合预测有助于消减单一预测的极端误差,基本计算原理如下：

设f1、f2是两个关于f的无偏预测值,fc是加权平均的预测值,预测误差分别为e1、e2和ec。取ω1和ω2为相应的权系数,且

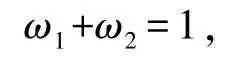
有

要求fc也是无偏的,其误差为：

记Var(e1)=σ11,Var(e2)σ22,cov(e1, e2)=σ12。

则两个预测方法的组合预测权系数分别为：

由于e1、e2相互独立,则σ12=0,有：

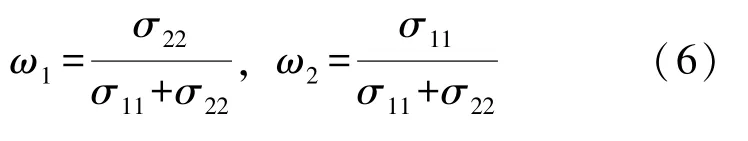
2 预测实证分析

本文针对云南地区电力需求进行预测分析,获取相关基础数据如表1所示：

2.1 基于多元线性回归的预测

本文结合多元线性回归预测模型的基本原理,构建以电力需求总量为因变量 (Y)、GDP(X1)及人口总量 (X2)为因变量的多元线性回归方程如下：

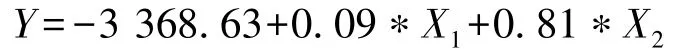
由此,对构建的多元线性回归预测模型进行预测精度计算分析,如表2所示：

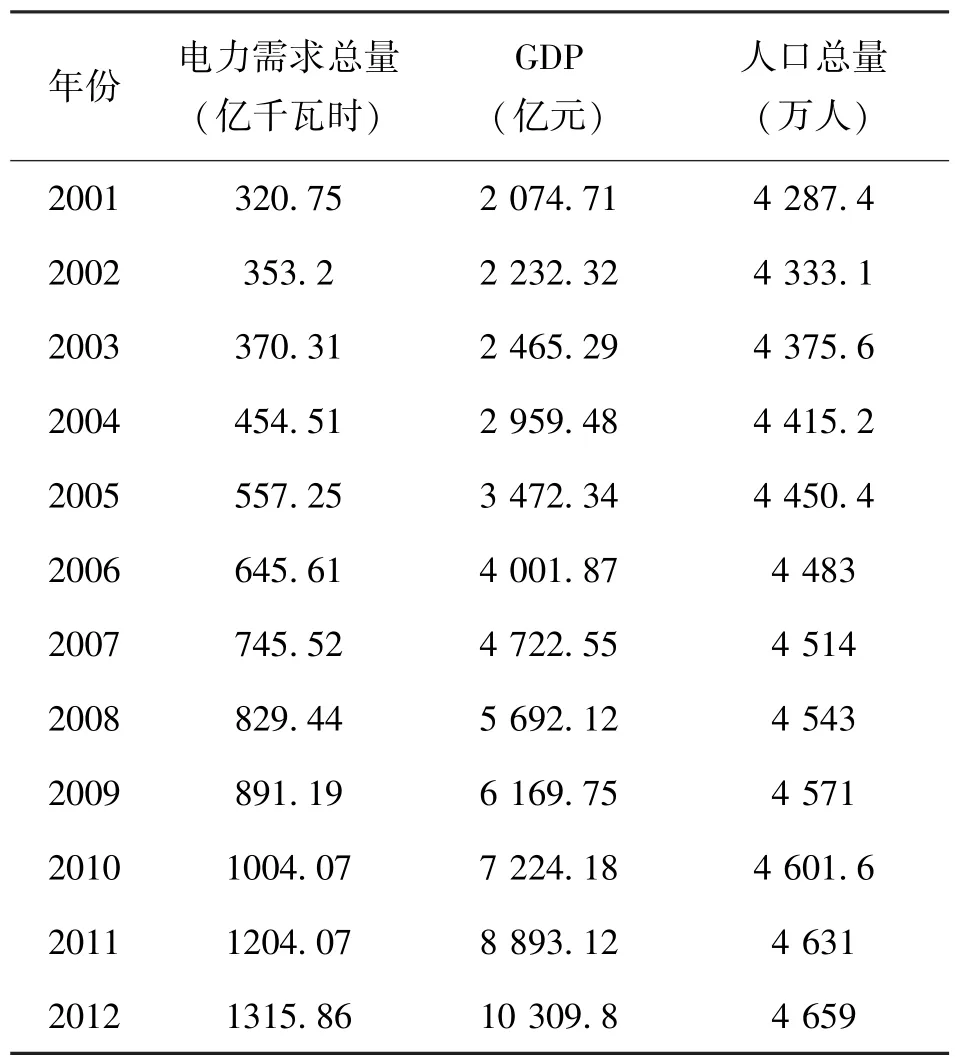
表1 云南地区电力需求及相关因素基础数据

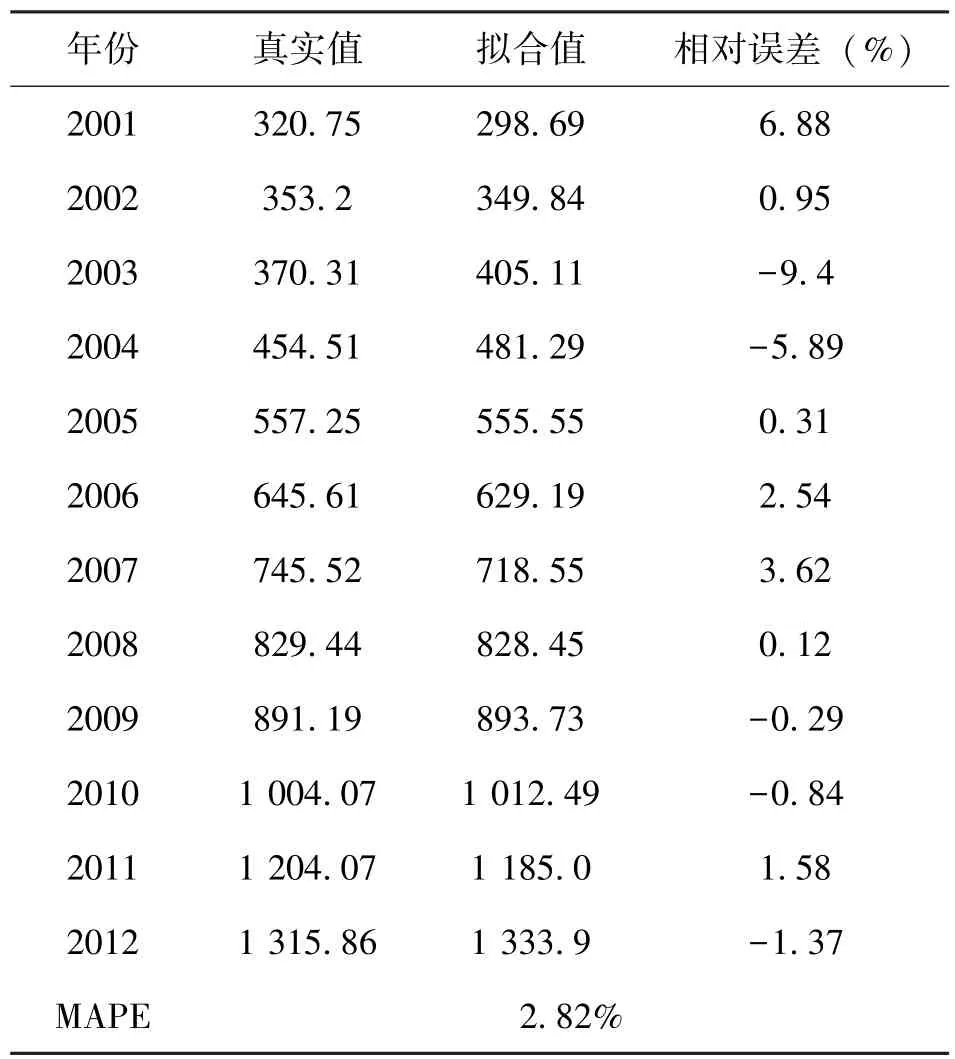
表2 多元线性回归预测模型预测结果分析

由上表中,平均相对误差MAPE值分析,所构建的多元线性回归预测模型预测精度较高,误差率低于5%,具有一定的预测效果。

2.2 基于灰色模型的预测

本文结合灰色预测模型的基本原理,依托历史数据,构建云南省电力需求中长期发展灰色预测模型,真实值与拟合值对比情况如下表所示：

表3 灰色预测模型预测结果分析

由上表中,平均相对误差MAPE值分析,所构建的灰色预测模型预测精度较高,误差率低于5%,具有一定的预测效果,但预测精度相比多元线性回归略有不足。

2.3 用电需求中长期发展组合预测

本文结合构建的基于MV发的组合预测模型基本思想,通过对上述两种预测模型的具体预测结果分析,得到两种方法的组合权重值如下：

综合分析云南地区电力需求发展变化情况,拟定GDP增长率保持平均水平为18%,人口增长率平均水平为0.6%,分别结合多元线性回归、灰色模型、组合预测模型对云南地区电力需求发展进行中长期预测分析,结果如下表所示：

表4 综合预测分析

由此分析,到2015年云南地区电力需求总量将达到 1 982.58亿千瓦时,2020年将达到 3 900.83亿千瓦时。因此,必须全面加强电力发展建设规划,推进电力基础工程建设,保障电力供给安全稳定。

3 结束语

本文以云南地区电力需求发展为研究对象,构建了基于多元线性回归、灰色预测及组合预测模型,并进行了对比计算分析,对未来云南地区电力需求发展进行了展望预测。综合以上分析,多元线性回归能够很好的兼顾经济、人口等其他相关因素进行综合分析,灰色预测模型具有较强的数据序列变化规律挖掘效果,利用组合预测模型能够很好地兼顾两种模型的特性及优势,进行更加科学、准确的预测分析。全面深化开展电力需求发展预测分析,利用先进的预测模型,能够很好地推动电力发展规划及基础建设工作,促进电力安全稳定发展。

[1]宋晓俊.吕梁市中长期负荷综合预测模型的研究 [D].北京：华北电力大学,2011.

[2]王学申,刘刚.电力系统负荷预测方法分析及应用 [J].中国科技信息,2011(11)：23-25.

[3]牛东晓,李春祥,孟明.基于灰色和偏最小二乘方法的年度负荷预测 [J].华东电力,2009,37(6)：989-992.

[4]陈金赛,张新波.基于改进BP人工神经网络的电力负荷预测 [J].杭州电子科技大学学报,2011,31(4)：173-176.

[5]于帆,吴彩红.中长期电网负荷组合预测研究 [J].计算机与数字工程,2011(3)：26-29.

[6]谢传胜,贾晓希,侯文甜.基于方法组合创新思想的电力系统长期负荷预测 [J].水电能源科学,2011,29(10)：207 -209.

Research on Medium and Long-term Development of Electricity Demand Based on the Theory of Combination Forecasting Methods in Yunnan Province

ZHANG Shaohui
(Yunnan Power Grid Corporation,Kunming 650011,China)

This paper base on analyzing the development of the electricity demand and the characteristics of economic and population in Yunnan province,and a method to improve the prediction based on a combination of forecast theory.

Yunnan province；electricity demand；combination of forecast；multiple regression；grey prediction

TM73

B

1006-7345(2015)01-0026-03

2014-07-15

张劭辉 (1979),男,硕士,工程师,云南电网公司,从事电网规划研究和管理工作 (e-mail)zsh_1979＠163.com。