数字网系方法并计及风电系统暂态稳定分析

范玉珍,刘延泉,孙丹

(华北电力大学自动化系,河北 保定 071003)

数字网系方法并计及风电系统暂态稳定分析

范玉珍,刘延泉,孙丹

(华北电力大学自动化系,河北 保定 071003)

为对风电场接入电力系统进行暂态稳定分析,提出了一种基于数字网系方法的电力系统暂态稳定性分析方法。该方法的采样值具有等分布性,可以改善输入随机变量分布空间覆盖程度,只需要较少的仿真次数即可快速估计输出随机变量的概率分布。选用IEEE39节点系统为例,建立风电场出力模型,并进行时域仿真。将本文方法分析结果与基于蒙特卡洛法的精确解进行了对比,对本文所提方法的准确性与快速性进行了验证,结果表明：数字网系方法解决了传统随机性分析方法计算次数多、仿真时间长、占用内存大的问题,它可以较好的估计输出随机变量的概率分布,能有效地处理系统运行中的不确定性问题.

数字网系方法；暂态稳定；风电场；不确定性

0 前言

随着风电等可再生能源的大规模并网,电力系统运行中的随机因素较之过去越来越多,加剧了系统的不确定性,暂态稳定分析也变得更复杂。目前,已有相关文献对含风电场的电力系统暂态稳定特性进行了研究。文献 [1]结合风电场接入系统实例,分析了大容量风电场接入系统后电网的暂态稳定特性。文献 [2]针对含双馈风电场的电力系统进行了暂态稳定性分析。

目前系统暂态稳定性分析的方法主要为蒙塔卡洛 (Monte Carlo)模拟法[3-4],Monte Carlo模拟法在采样规模足够大时具有很高的精度,但耗时长,因此它通常作为一种标准方法来评价其它方法的精度。为了提高计算效率,文献 [5]采用点估计法根据已知输入随机变量的概率分布,求取输出随机变量的各阶矩,该方法虽然具有较快的计算速度,但其输出随机变量的高阶矩误差较大。文献 [6]提出了一种基于TPNT的计及输入变量相关性的半不变量计算方法,该方法由输入随机变量的概率密度函数得到其半不变量,进而采用半不变量代数运算代替卷积运算,提高了计算效率,但要求输入随机变量相互独立或满足线性关系。

数字网系方法属于拟蒙特卡洛法 (quasi-Monte Carlo)的一种,相较于蒙特卡洛模拟的伪随机序列,它生成的拟随机序列的点列分布更加均匀,因而在数学领域得到广泛的应用。对大规模风电场接入电力系统,本文提出一种基于数字网系方法的电力系统暂态稳定分析计算方法,借助数字网系方法良好的等分布抽样特性,只需较少的抽样次数就可以得到更精确的结果。和传统的Monte Carlo方法相比,可以在保证计算精度的同时减少计算时间,更准确高效地研究计及风电的电力系统暂态稳定性。

1 数字网系方法

数字网系方法是一种拟蒙特卡洛法,它可以看做是与Monte Carlo方法相对应的确定性方法,该方法通过确定性采样产生的低差异序列比Monte Carlo方法产生的随机序列分布更加均匀,在相同采样规模下,从而获得比传统的 Monte Carlo方法更高的模拟精度。图1为蒙特卡洛模拟和拟蒙特卡洛模拟产生的区间内的二维随机数,比较两种方法产生的随机数的分布,可以看出,拟随机序列要比伪随机序列的分布均匀的多。

图1a 蒙特卡洛模拟生成的二维伪随机数列

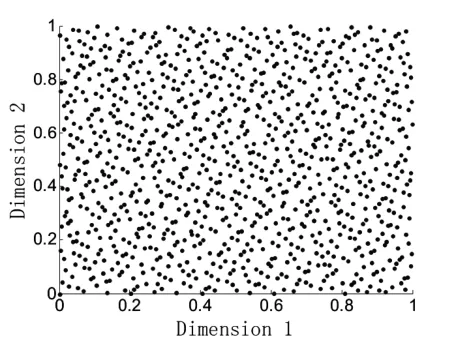
图1b 拟蒙特卡洛模拟生成的二维伪随机数列

van der Corput序列是最基本的拟随机序列。它选择大于等于2的一个素数b为基,将一系列数表示成这个基的位数的形式,然后将这些数位逆序排列再在前面加上小数点而得到的值,最后再转换成十进制的形式。

取一非负整数n在数基b(整数b≥2)下表示为：

式中：aj(n)∈B,B={0,1,···,b-1}；m为满足如下条件的最小整数：aj(n)=0,∀j＞m。

为了把n转换成小数点的形式,我们定义如下函数：

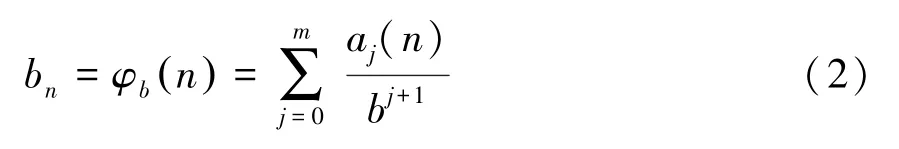
表1给出了样本数为8的2进制 van der Corput序列。由表1可以看出,对于任意的bm个连续点,每个点分别落在长度为 1/bm的区间[k/bm,(k+1)/bm)]中。m为非负整数且bm≤N, N为样本数,k=0,1,···,bm-1。例如对于表1中任意4个连续的点,每个点分别落在区间[k/4,(k+1)/4)]中,其中k=0,1,2,3。上述连续点的分布规律体现了van der Corput序列的均匀性。

表1 样本数为8的van der Corput序列

一些广义化的van der Corput序列被引入来解决多维问题,如Halton序列、Faure序列、数字网系等,其中效果最令人满意的是数字网系。本文算例采用2进制的数字网系方法进行计算,形成点列中第个点 (j=1,···,s；n=1, ···)的步骤如下：

1)把第N-1个整数用2进制数表示,即

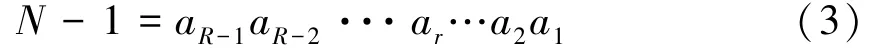
其中ar∈B,B={0,1,···,b-1},R为满足bm≤N的m的最大值。

2)对N-1=aR-1aR-2···ar…a2a1进行排序,得到排序后的序列[d1d2···dr···dR]T为

由数字网系方法得到的点服从[0,1]上的均匀分布,如果所研究的随机输入变量服从其它分布,则需要根据相应的累积分布函数的逆函数将这些点转换成其它分布 (如威布尔分布)。

2 风电场风机出力模型

本文假设风速服从威布尔分布,式 (6)所示为威布尔分布的概率密度函数[7],式 (7)所示为风电场出力分段函数表达式：

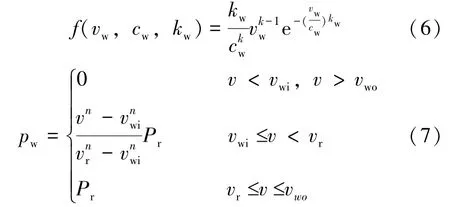
式中：vwi为切入风速；vwo为切出风速；vr为额定风速；Pr是风机额定出力；n为风速-功率系数,理想值为3。风机简化处理为PQ节点,即作为负的负荷接入PQ节点。

3 计算步骤

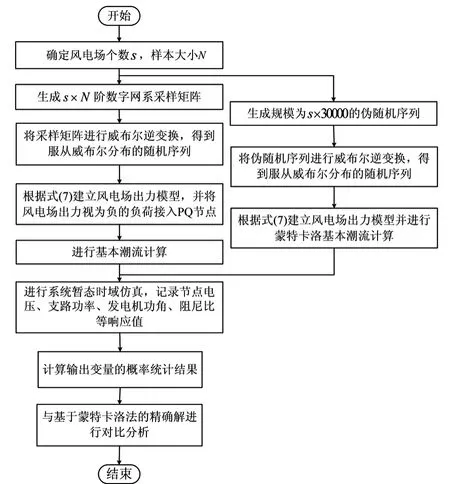
图2 计算流程图

1)确定风电场个数s及样本大小N。

2)根据第2节所述方法形成采样点矩阵。

3)采用威布尔分布函数的逆函数将服从均匀分布的样本变换到服从威布尔分布空间的采样样本。

4)建立风电场风机出力模型,并作为负的负荷接入PQ节点。

5)进行系统基本潮流计算。

6)进行系统暂态时域仿真,记录节点电压、支路功率、发电机功角、阻尼比等响应值。

7)计算相应输出变量的概率统计信息。

8)将统计结果与基于蒙特卡洛法的精确解进行对比分析。

4 算例

本文采用IEEE39节点测试系统,对计及风电的电力系统的暂态稳定进行不确定性分析,分析主要针对风电场接入后主要输电线路发生三相短路故障情况进行,通过Monte Carlo方法来对比验证数字网系方法的仿真结果。

IEEE39节点系统参数参见文献 [8]。本算例接入两个风电场,为简化计算,设切入风速为4 m/s,切出风速为25 m/s,平均风速为13 m/s,风机形状参数为1.7,尺度参数为9.8,装机容量均为100 MW。两风机分别接入节点3、4,系统负荷采用恒阻抗模型,支路10-11靠近节点11处发生三相短路故障,故障发生在1 s时刻,断路器在1.2 s将故障切除。

假设30 000次Monte Carlo方法计算得到的结果为准确值,并与采样规模500次的数字网系方法得到的结果相比较。选择发电机相对功角和节点电压作为暂态输出响应,通过对比两种方法所得发电机相对功角以及关键节点电压的期望来验证本文所提方法的准确性和快速性。

图3、图4为两种方法仿真得到的风电场接入节点和故障侧节点的电压幅值的期望值曲线,图5为两种方法得到节点34发电机相对功角期望值曲线。由图可以看出,两种方法所得结果趋势一致,数字网系方法计算所得功角、节点电压期望值与Monte Carlo方法计算结果近似,证明了数字网系方法的准确性。

结果分析：图3(a)为风电场接入节点3的电压,故障前节点3的电压为1.03 pu,故障时电压跌至0.85 pu,故障清除后恢复到1.02 pu,表明该风电场具有较好的低电压穿越能力,能够保证不脱网连续运行。图3(b)为风电场接入节点4的电压,故障前节点4的电压为1.01 pu,故障发生后跌至0.74 pu,故障清除后瞬间恢复到0.99 pu,表明该风电场也具有低电压穿越能力,在故障发生前后始终能保持并网运行。图4为故障侧节点11的电压,节点11在故障时电压跌至0.63 pu,跌落0.2 s后恢复至0.99 pu,经过4.2 s后电压稳定。

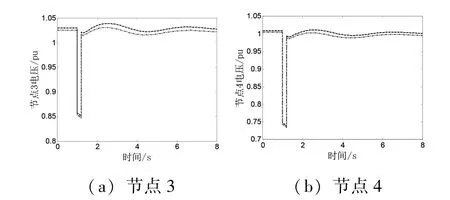
图3 风电场接入节点电压期望值

图4 故障侧节点电压期望值

图5 节点34发电机相对功角期望值

图5为节点34发电机的相对功角期望值的变化曲线,由图可以看出,发电机的相对功角在第一摆和第二摆的角度并没有不断增大,而是整个过程呈现振幅衰减,可见系统暂态功角稳定。

表2对比分析了本算例两种方法的仿真时间,由表可以看出,30 000次的Monte Carlo方法仿真时间远远高于数字网系方法的时间,体现了数字网系方法计算的快速性。

表2 两种方法仿真时间

5 结束语

为分析风电场接入电力系统的的暂态稳定概率统计特性,将数字网系方法应用于系统暂态时域仿真中。IEEE39节点仿真结果表明本文所提方法计算速度快、准确性高,与传统Monte Carlo方法相比,能快速计算含风电场系统暂态稳定概率统计特性,为暂态稳定分析提供重要的参考。

[1] 张红光,张粒子,陈树勇,等.大容量风电场接入电网的暂态稳定特性和调度对策研究 [J].中国电机工程学报, 2007,27(31)：45-51.

[2] 盛超,曾杰,郝正航,等.含双馈风电场电力系统暂态稳定性分析 [J].电力系统及其自动化学报,2012,24 (1)：133-137.

[3] 陈雁,文劲宇,程时杰.考虑输入变量相关性的概率潮流计算方法 [J].中国电机工程学报,2011,31(22)：80 -87.

[4] 范荣奇,陈金富,段献忠,等.风速相关性对概率潮流计算的影响分析 [J].电力系统自动化.2011,35(4)：18 -22.

[5] 杨欢,邹斌.含相关性随机变量的概率潮流三点估计法[J].电力系统自动化,2012,36(15)：51-56.

[6] 刘小团,赵晋泉,罗卫华,等.基于TPNT和半不变量法的考虑输入量相关性概率潮流算法 [J].电力系统保护与控制,2013,41(22)：13-18.

[7] 王敏,丁明.考虑分布式电源的静态电压稳定概率评估[J].中国电机工程学报,2010,30(25)：17-22.

[8] Milano F.Power System Analysis Toolbox documentation for PSATversion2.1.6[EB/OL].2011.http：// www.uclm.es/area/gsee/Web/Federico/past.htm.

Analysis on Transient Stability of Power System Integrated with Wind Farm Groups Based on Digital Nets Method

FAN Yuzhen,LIU Yanquan,SUN Dan
(Department of Automation,North China Electric Power University,Baoding,Hebei 071003,China)

To analyze the transient stability of power system integrated with wind farm groups,this paper applied Digital Nets method to compute system’s transient stability.Digital Nets method which has equidistributed sample values is applied to improve the sample values coverage of random variables input spaces.The accuracy and validity of proposed method are tested on IEEE 39 bus system which the wind farm power modeling on the platform and the simulation results show that Digital Nets method can rapidly estimate the probability distribution of the output random variables compared with the traditional approaches which need more number of calculation times,long simulation time and need of memory space.

digital nets；transient stability；wind farm groups；uncertainty

TM74

B

1006-7345(2015)01-0014-04

2014-11-25

范玉珍 (1988),女,硕士研究生,华北电力大学,研究方向为电力系统分析计算、运行控制；大规模间歇式电源并网分析；电力系统规划设计；风能、太阳能并网发电与电力系统交互影响 (e-mail)yuzhen_f＠163.com。

刘延泉 (1963),男,硕士生导师,副教授,华北电力大学,主要从事协调控制系统优化、DCS及其应用等方面工作 (email)composer_liu2000＠yahoo.com.cn。

孙丹 (1989),女,硕士研究生,华北电力大学,研究方向为电力系统分析计算、运行控制；大规模间歇式电源并网分析；电力系统规划设计；风能、太阳能并网发电与电力系统交互影响(e-mail)sundan_believe＠163.com。