“三维五步教学法”在高中数学概念课教学中的应用
2015-12-12吴俊英
吴俊英


中图分类号:G633.6 文献标识码:A 文章编号:1002-7661(2015)24-0018-02
为了能更好地实现学生的全面发展,培养学生自主学习、学会学习的能力,逐渐改变学生的学习方式,提高思维能力,激发学生学习的自觉性、主动性以及合作意识。最终达到学生主动参与和自主学习的目的,从而提高课堂学习效率。我所在的厦门实验中学提出了“三维五步教学法”,现将在幂函数这一新课教学所做的尝试整理如下:
一、课前准备
(1)教师提供教学资源。教师提供了一份双面A3导学案加10分钟的幂函数概念教学微课视频。
(2)学生用网络电脑学习教学资料,到指定的平台下载资源,然后尝试理解、思考所获得的信息,尝试归纳知识要点。
二、课堂教学
(一)问题引入
先来看几个具体问题:分析以下五个函数,它们有什么共同特征?
(1)边长为a的正方形面积S=a2,S是a的函数;
(2)面积为S的正方形边长a=S,a是S的函数;
(3)边长为a的立方体体积V=a3,V是a的函数;
(4)某人ts内骑车行进了1km,则他骑车的平均速度v=t-1km/s,这里是的函数;
(5)购买每本1元的练习本w本,则需支付p=w元,这里p是w的函数。
(二)新知讲解
1.幂函数的概念:一般地,我们把形如y=xa(a∈R)的函数称为幂函数,其中x是自变量,a是常数。
例1.已知y=(m2+2m-2)·x+2n-3是幂函数,求m、n的值。
练习1:判断下列函数有哪些是幂函数?
(1)y=;(2)y=3x2;(3)y=x3-x;(4)y=x-;(5)y=;(6)y=3.
练习2:已知幂函数y=xa的图像过点(2,),求出这个函数的解析式 .
【设计意图】问题引入是利用教材的材料,引导学生从具体实例中归纳,类比指数函数、对数函数的形式定义,得出幂函数的一般特征;例题及练习是为了学生明晰概念,学以致用。练习1为形式判断,练习2为巩固待定系数法,强化方程思想。
【导学案及课堂实施情况反馈】本部分导学案情况完成良好,实际教学时主要是实物投影学生导学案作业,老师个别提问再加以分析讲解。而更好的做法是,投影时可以由学生来讲解,充分调动学生积极性,也体现了学生主体地位。
2.常见幂函数的图像和性质
(1)幂函数的图像
问题:在同一平面直角坐标系内作出下列函数的图象:(1)y=x;(2)y=x;(3)y=x2;(4)y=x-1;(5)y=x3。从图象分析出幂函数所具有的性质。
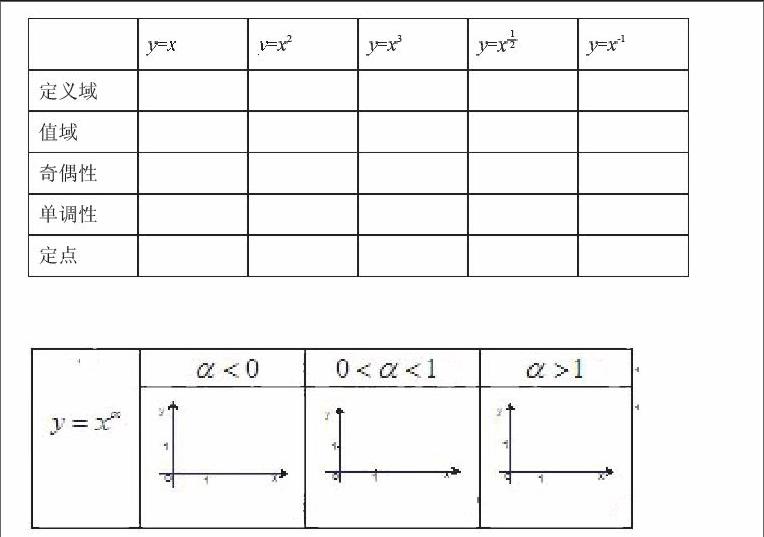
观察图象,总结填写下表:
①画出幂函数在第一象限的图象,其规律如下:
②根据 幂函数的奇偶性作出其它象限内的函数图象。
(2)幂函数的性质 (仅限于在第一象限内的图象)
反思:a.怎样求出幂函数的定义域和判断幂函数的奇偶 性?
b.怎样画出幂函数的图象?
【设计意图】培养学生的作图能力,以及借助图像分析函数性质的能力。
【导学案及课堂实施情况反馈】学生作图水平参差不齐,在定点、凹凸性上存在较大漏洞,尤其是y=x2与y=x3在直线x=1左右的上下位置关系。在教学时投影了图形绘制较好的几个作品,再由小组合作交流完善导学案上学生自己的图形,增加学生学习的信心。在由特殊推广到一般情况时,学生对0
例2.给定一组函数的解析式:①y=x;②y=x;③y=x-;④y=x-;⑤y=x;⑥y=x-;⑦y=x,如右图的一组函数图象,请把图象对应的解析式序号填在图象下面的括号内。
练习3:函数y=x的图象是( )
【设计意图】从探究幂指数是正分数的幂函数的图象和性质做好铺垫,再让学生通过类比,自主探究幂指数是负整数和负分数的幂函数的图象和性质,使学生的学习过程成为教师引导下的“再创造”过程。启发学生总结出幂函数随幂指数变化的分布规律。
【导学案及课堂实施情况反馈】学生对根式与分数指数幂的转化存在困难,对于一般幂函数的定义域和判断幂函数的奇偶性的判断存在困难,因此本例题耗时较久,最后还是由教师讲解,而不是学生自主探究,主要还是课堂时间限制,老师为了讲解后面的例题而没有给学生留足探究时间。
例3.比较下列各组数的大小。
(1)2.3 与2.4 ; (2)0.31 与0.35 ;
(3)()-与()-;(4)(-)-与(-)-。
练习4:比较0.850.5,0.90.5,0.9-0.5的大小。
【设计意图】幂函数性质的应用,巩固之前“比较大小”题型的常见解法:构造函数利用函数单调性,或借助中间量比较大小。
【导学案及课堂实施情况反馈】学生答题过程表述不到位。课堂因为临近下课只来得及简要分析,同样是投影学生完成较好的作品,以起到示范作用。
(三)课堂小结
由六个小组各自讨论交流小结,再派代表发言。
【设计意图】提纲契领,锻炼学生归纳、表达能力。
【导学案及课堂实施情况反馈】实际课堂来不及实施。
三、课后反思
1.利用导学案的“三维五步教学法”模式下的数学概念教学是一种知道谜底看谜面的过程,数学概念的生成过程中的神秘感有所降低,数学概念的发生发展过程就无法在课堂上展现。到底,概念课堂的问题串应如何逐层展开,逐级递进设计,值得深究。
2.在幂函数的教学中,教师应该围绕发展学生能力这个核心,选择好载体,适当拓宽也是未尝不可的。判断我们的教学是否恰当,唯一的标准就是通过学习是否促进学生能力的发展。本课的例题2就是为了进行拓展,但变式变多,可适当删减一下,效果更好。
3.幂函数是概念课,在分析函数性质的基础上,能绘制常见几个幂函数的图象,通过图象观察和归纳一般的性质,促进对概念的理解,体会研究方法。在教学过程中,应当侧重图象教学,应当详尽展示过程,体现研究性学习,关注课堂生成,删减例题及练习,留足时间给学生充分展示。
4.“学生在教师的带领下开展探究活动”这样的话教师也经常会说,但实际的情况是教师有所取代,本课中也是不自觉就出现“教师代替学生分析,代替学生探究”的现象。因此,教师应时刻记得:“教”的教程中,教师也不要“一言堂”,老师教的方式是:让会的学生讲,讲对的不重复,讲得不完整的补充,讲错的改正。对学生在预学“导学案”中暴露的错误,让会的教不会的,开展“兵”教“兵”“一帮一”的活动。教师只做评定和补充。
5.课堂评价关注对学生个人的评价,而忽略了对小组合作的评价,评价的方式也不够多样化。上课速度较快,留给学生独立思考、反馈的时间较短,对学生预习效果要求较高,对于后进生学习比较吃力。
(责任编辑 陈 利)
