基于ANSYS的压电陶瓷振子横向效应分析
2015-12-11于栋杜斌严有琪
于栋 杜斌 严有琪

摘 要:该文运用ANSYS对导波检测时所使用的矩形pzt-5H型压电片陶瓷振子进行了谐响应分析和瞬态分析,瞬态分析时加载汉宁窗调制的音频信号。首先通过谐响应分析确定了压电陶瓷振子横向效应的谐振频率,然后通过瞬态分析分析了压电陶瓷振子的瞬态响应能力。结果表明,汉宁窗调制的音频信号能够驱动压电陶瓷振子振动,但表现出迟滞现象。
关键字:压电陶瓷 ANSYS 瞬态分析 汉宁窗
中图分类号:TM359 文献标识码:A 文章编号:1672-3791(2015)08(a)-0035-03
Transverse Effect Analysis on Piezoelectric Ceramic Vibrator Based on ANSYS
Dong Yu1 Bin Du1,2 Youqi Yan1
( 1. Special Equipment Safety Supervision Inspection Institute of Jiangsu Province,Zhenjiang 212013,China;2. School of Mechanical Engineering,Jiangsu University,Zhenjiang,Jiang Province,212013,China)
Abstract:In this paper, harmonic and transient response of Rectangular PZT-5H Piezoelectric ceramic vibrator, which were used to excite guided wave, were researched based on ANSYS, hanning window modulated audio signal were loaded during transient analysis.First,the resonant frequency of the piezoelectric vibrator transverse effect were researched by harmonic response analysis. Then transient response ability of piezoelectric ceramic vibrator were analyzed by utilizing transient analysis. The results show that the hanning window modulated audio signal were able to drive the piezoelectric ceramic vibration, but show the hysteresis phenomenon.
Key Words:Piezoelectric ceramics; ANSYS; Transient analysis; Hanning window
超聲导波在长距离检测例如管道检测中有较明显的优势,在结构的一点激励超声导波,由于导波衰减小,传播的距离很远,因此一次检测的距离较大;同时由于超声导波在被检工件整个壁厚范围内存在,因此是对工件进行的整体检测。
在激励纵向模态导波时,利用了压电陶瓷振子的横向效应,即长度方向伸缩振动。试验前需要对压电振子进行振动分析,传统的解决方法是建立振子的自由振动方程,用解析方法解答。然而,这些方法数据处理起来比较繁琐,而且处理的结果不够直观[1]。借助ANSYS可以直观的对压电振子进行振动分析,ANSYS中ANSYS Multiphysics或者ANSYS mechanical软件包提供了压电分析,可以进行稳态、模态、预应力模态、谐波、预应力谐波和瞬态分析。
1 压电陶瓷常用振动模式
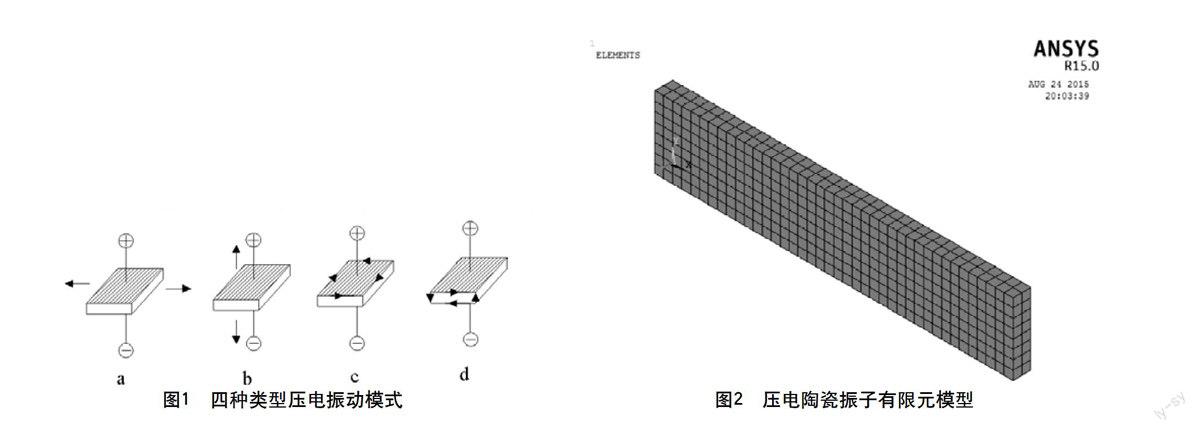
当施加不同方向的极化方向和电场方向时,压电振子会表现出不同的振动模式,如图1所示为四种类型的压电振动模式[2]:图1(a)、(b)为厚度方向极化,图1(c)、(d)为宽度方向极化;全部为厚度方向施加电场。压电陶瓷常用的振动模式分别为:
(a) 垂直于电轴方向伸缩(长度伸缩),简称为LE;
(b) 平行于电轴方向伸缩(厚度伸缩),简称为TE;
(c) 垂直于电轴的面内切变(面切变,又称轮廓切变),简称为FS;
(d) 平行于电轴的面内切变(厚度切变),简称为TS。
根据弹性波传播方向与电轴方向之间的关系,可将压电陶瓷振动方式分为两种:传播方向垂直于电轴方向,称为横向效应包括LE模式和FS模式;传播方向平行于电轴方向,称为纵向效应包括TE模式和TS模式。根据纵向导波激励和接收的理论,激励和接收纵向模态导波时所使用的是压电陶瓷振子长度方向伸缩模式,即图1(a)所示LE模式。
2 ANSYS模型建立
2.1 压电陶瓷的输入参数
压电分析采用第二类压电方程:
(1)
其中,T,S 表示应力和应变矢量;D,E 分别表示电位移矢量和电场矢量;e,cE,S 分别表示压电应力系数、压电弹性系数和压电介电系数。
压电陶瓷片选用pzt-5A型进行分析,其模型的输入参数分别为[3]:相对介电常数矩阵[]=,压电应变系数矩[d]=(10-12m/v),压电刚度矩阵[c]=(1010N/m2)。
分析时选用solid226单元,keyopt(1)=1 001。solid226为20节点6面体单元,采用高阶单元(中间节点形式二阶单元),与solid5相比,分析精度提高,改善了分析准确性。
2.2 压电陶瓷模型建立
在ANSYS前处理模块,采用自上而下的建模方式,直接生成长方形压电陶瓷振子模型。压电陶瓷振子的尺寸为20 mmX4 mmX1 mm。采用solid226单元进行并且运用扫略的方式进行网格划分,控制网格单元尺寸为0.5mm,最终生成的模型如图2所示,模型中包含640个单元,3 909个节点。
3 谐响应分析
3.1 谐响应分析简介
谐响应分析是用于确定线性结构在承受随时间按正弦(简谐)规律变化的载荷时的稳态响应的一种技术。分析的目的是计算出结构在几种频率下的响应并得到一些响应值(通常是位移)对频率的曲线。谐响应分析可采用三种方法:完全法(Full)、缩减法(Reduced)、模态叠加法(Mode?Superposition)。其中完全法使用简单,并且使用完全矩阵,不涉及质量矩阵的近似,求解准确,该文将使用完全法进行压电陶瓷的谐响应分析。
3.2 边界条件与加载
该文主要分析压电陶瓷在自由条件下的横向效应,因此不对模型施加位移约束。为了模拟实际中的电极面,分别耦合z轴上下表面电压,耦合电压后的表面在以后的分析过程中始终保持电势相同。谐响应分析时需要设置载荷的幅值和相位,因此加载条件为:z轴下表面接地,上表面加载电压幅值为20 V,相位为0,即正弦信号。
3.3 结果分析
提取1242节点(0,0.002,0.001)x轴方向的位移Ux随频率变化的曲线图,如图3所示,放大70 KHz至85 KHz的位移图,可以观察出1242节点在77 KHz时位移最大,即在77 KHz时压电陶瓷产生谐振。如图4所示,模型77KHz下的变形图,实体为变形前模型,虚线为变形后模型。可以得出在外加77 KHz正弦函数激励时,模型主要振动方式为长度方向伸缩振动,即LE模式。
通过谐响应分析可以分析模型在外加不同频率的正弦变化的载荷时的振动模式。该文通过分析20 ~200 KHz之间模型的谐响应的出了模型在77KHz下进行长度方向伸缩谐振。
4 瞬态分析
4.1 瞬態分析简介
瞬态分析又称时间历程分析,是用于确定承受任意的随时间变化的载荷的结构动力学响应的一种方法。对于压电瞬态分析,为使求解稳定应用TINTP命令设置积分参数ALPHA=0.25、DELTA=0.5和THETA=0.5[4]。
4.2 加载设置
导波激励时通常使用经过汉宁窗调制的音频信号。与正弦音频信号相比,经过汉宁窗调制的音频信号的能量高并且能保持较窄的频带,这有利于长距离检测和激励单一模态的导波[5]。该文中加载的信号为经过汉宁窗调制的10周期音频信号,加载信号如图5所示。加载条件为z轴下表面接地,上表面加载图5所示的信号。
4.3 结果分析
为研究模型在加载图5所示信号下的响应,提取了节点1242在x轴方向随时间变化的位移图,如图6所示。由图6可知,在加载调制的音频信号后,压电陶瓷按照调制音频信号的变化规律变化,说明调制的音频信号能够驱动压电陶瓷片发生振动。对比图5和图6可知,在加载10个周期的音频信号后,在对应的时间内压电陶瓷振子在x轴方向的振动并不是完整的10个周期,这是由于压电陶瓷的迟滞性所致的[6]。
5 结语
该文运用ANSYS软件对矩形压电陶瓷振子的横向效应进行了分析,分别进行了谐响应分析和瞬态分析。通过谐响应分析确定了压电陶瓷振子横向效应的谐振频率。瞬态分析时加载了频率和谐振频率一致并经过汉宁窗调制的音频信号,结果表明经汉宁窗调制的音频信号能够驱动压电陶瓷振子振动,但是表现出一定的迟滞性。该文没有研究压电陶瓷迟滞性对导波激励的影响,还有待进一步探究
参考文献
[1] 罗平.基于ANSYS 模态分析的压电陶瓷参数数据的转换及其输入[J].广东技术师范学院学报,2009(9):11-15.
[2] 韩宝坤,孙超,吕航.基于ANSYS 的纯压电振子瞬态特性分析[J].微特电机.2012,40(4):35-37.
[3] 魏胜.基于ANSYS 的压电换能器有效机电耦合系数的仿真分析[J].深圳职业技术学院学报,2012,11(3):7-12.
[4] 吕航,范明庆,孙超,等.基于ANSYS 的矩形压电振子瞬态特性分析[J].微特电机,2012,40(3):34-37.
[5] Jennifer E. Michaels, Sang Jun Lee, Anthony J. Croxford, et al. Chirp excitation of ultrasonic guided waves[J].Ultrasonics,2013,53(1):265-270.
[6] 王社良,曹文华,樊禹江.基于ANSYS的新型压电陶瓷管驱动器的性能分析与研究[J].材料导报B:研究篇,2012,26(12):154-157.
