浅析基于位移反分析法的隧道支护研究
2015-12-11叶欣
叶 欣
(泉州市住房和城乡建设局总工程师办公室 福建泉州 362000)
引 言
随着城市建设的不断扩大,修建城市道路往往以隧道的形式穿越山体,这样缩断了行程,改善了城市的交通环境。开凿隧道,首选碰到的问题就是对岩体的支护,然而我们已经很难测量应力分布,无法确定应力场和围岩的力学参数,更不用说断层,褶皱等构造应力,应力情况错综复杂,而设计要求越来越高,工程师们更是无法入手。以往的理论,利用弹性理论压力隧道模型,认为其上覆的荷载按上覆的岩土的自重应力近似,在直径的八倍的范围处忽略自重,如(图1)[1]。而影响隧道围岩二次应力状态因素很多,如岩体的初始应力状态,岩体的构造,洞室的形状尺寸,洞室的埋深和开挖施工技术等[2]。往常做法是在野外地质调查的基础上,在现场进行必要的岩体力学试验和地应力测试,再将测试结果用于理论计算。另外应力的释放是通过四周的物体进行传播,因此受到物体的质量和形变速度影响,就要求力传感器足够小且柔软而不至于影响物体之间的相互接触[3]。这就造成测量的仪器昂贵。近年来位移反分析法不断完善,已成为了解决复杂岩石工程问题的主要方法,并用于隧道的分析研究,利用位移反分析法来解决上述问题,它通过可靠性理论的岩土工程参数来确定反分析设计参数[4]。随着科学技术的进步,尤其是信息技术和计算机技术的发展,大量的数据采集,复杂的矩阵计算都可以通过计算机解决,通过数值分析的软件,构建物理模型,对分部工程进行定量分析,描述该过程,从而得出数量指标,为设计提供参数。计算机还可以仿真模拟某个过程,用动画形象的表现整个过程,对工程隐患进行预测。

图1 地下应力
1 位移反分析
反分析法是指求解反问题,即通过测量某些部位的响应,如位移、速度、加速度或应变等,来确定冲击点处的冲击力。
人们在研究位移反分析法中取得了重大的成就。从1915年哈斯特测定初始地应力开始,开创了通过现场量测信息反演算岩土工程。位移反分析的基本思想是由Karanagh在1971年提出的,基本方法是根据现场实测的位移,利用有限元方法来计算岩体的力学参数。日本学者Sakurai在1974年根据围岩的蠕变位移,使用解析方法计算了岩体的粘滞性系数。1983年,我国学者冯紫良、杨林德提出了一种方法,位移反分析的有限元分析方法,它将地应力分为均布构造应力和自重应力,用有限元方法求自重应力场产生的围岩位移差值,反算岩体的均布构造应力。孙钧1992年提出了局部最优解和全局最优化解的概念;徐日庆1994年在研究土的应力路径非线性行为时采用正反分析法确定了模型参数。令人可喜的是国内反分析研究已赶上了国际发展水平[5]。
2 有限元的反演分析
弹性问题优化反演分析法中,目标函数取为:
未知量为初始地应力分量和综合弹性模量,在待求量与量测数据信息间建立线性方程组:[K]{x}={y}式中:{x}为待求未知量列阵;{y}为与量测信息已关的已知量列阵;[K]为未知量的影响系数阵。
岩土体的力学性质及各种因素的综合作用,可表示如下[6]:

式中σ,τ—地应力分量;
μ,E—岩体的泊松比、弹性模量;
c,φ—岩体的内聚力、内摩擦角;
η,t—岩体的粘滞系数、时间。
反分析采用不同的本构关系(应力与应变之间的关系式),同时可得到不同的力学特性参数,如弹性参数(弹性模量 E、泊松比 μ 等)[7]。
有限元二维有限元力学分析模型,一般采用外加载模型、倒转应力模型和原岩应力模型相结合的方法进行分析,岩体原岩应力量测原理决定了所采用的力学模型为外加模型[8]。
3 工程算例
工程为城区内某一在建隧道。山势较高,岩体为花岗岩,地质条件复杂,隧道较长,工期紧、任务重、技术复杂。其为隧道监测布设如(图2)所示。
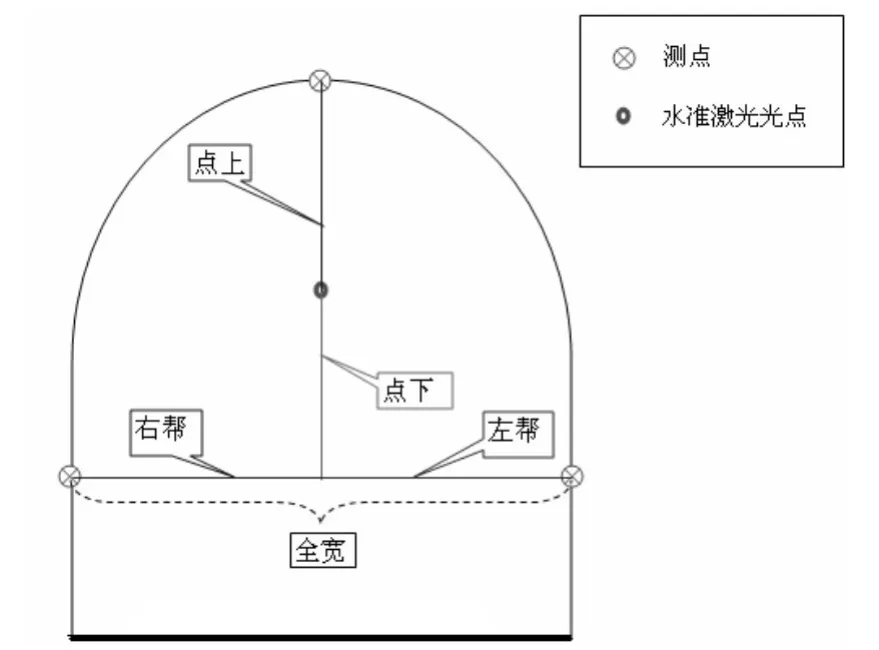
图2 监测布设图
数据:

2.1 2.15 2.1 1.85点下 2.3 2.3 2.05 2.25左帮 2.73 2.71 2.71 2.85右帮 2.5 2.51 2.68 2.57全宽 5.23 5.22 5.39 5.42点上 2.05 2.1 2.1 1.7点下 2.26 2.15 2 2.2左帮 2.73 2.71 2.71 2.82右帮 2.45 2.47 2.68 2.53全宽 5.18 5.18 5.39 5.35点上 2.05 2.05 2.1 1.65点下 2.25 2.1 2 2.15左帮 2.72 2.7 2.71 2.8右帮 2.45 2.47 2.68 2.48全宽点上5.17 5.17 5.39 5.28
计算理论依据:
此为隧道的平面应变问题,因此沿隧道长度方向定为z轴,它的应变为0,此方向上的剪应力为0,结构有限元理论中 σz=μ(σx+σy),因此只要求出 σx,σy,τxy。在考虑平面二维受力的情况下,
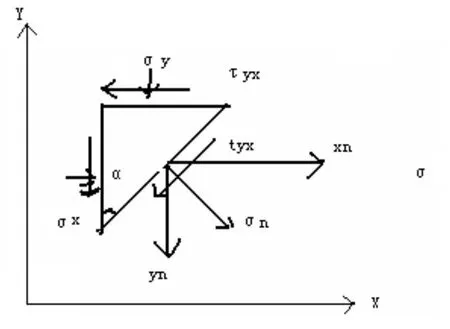
图3 平面应变
应用结构有限元方法,节点的受力只有横向和纵向 Xn,Yn,等效于 σx,σy,τxy,
做一点的坐标应力边界转化,
设:l为 cos(α),m 为 sin(α)

ds是很小=0
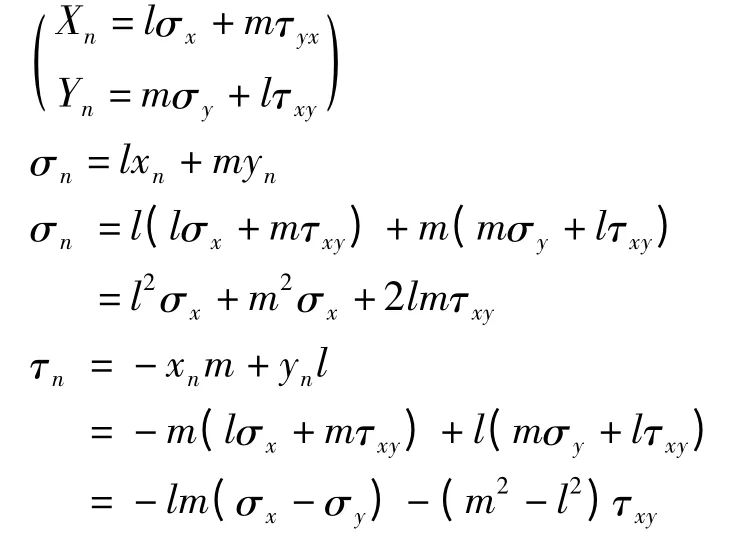
根据结构有限元的计算公式得出

其中[F]是各点的力矩阵,设n各节点,[F]为阶矩阵,[K]是节点刚度矩阵,为2n×2n矩阵,[δ]是位移矩阵为2n×1矩阵。
通过ansys进行模拟计算
选取上面位移最大的观测值进行分段,并且测量各个段的位移值。本文仅把支护结构进行简要划分,分成21个单元,21个节点,其中1、17节点重合。

图4 分段
每个单元有4×4单元刚度矩阵。
例如20单元的刚度矩阵为
1 0.4009987E+09 0.1236157E+10
-0.4009987E+09 -0.1236157E+10
2 0.1236157E+10 0.3810695E+10
-0.1236157E+10 -0.3810695E+10
3 -0.4009987E+09 -0.1236157E+10
0.4009987 E+09 0.1236157E+10
4 -0.1236157E+10 -0.3810695E+10
0.1236157 E+10 0.3810695E+10
而后测量各个节点的位移
X方向的位移
-0.1767 -0.2074 -0.1955 -0.1968
-0.2038 -0.1338 -1.174 -0.1503
-0.0748 -0.0571 -0.2808 -0.1042
-0.2147 -0.2362 -0.2201 -0.1829
-0.1767 -0.366 -0.3298 -0.1383
-0.2125
Y方向的位移
0.1745 0.158 0.0542 0.0312
0.0881 0.152 0.23 0.1673
0.099 0.0928 0.1423 0.0954
0.1506 0.1493 0.1672 0.1213
0.1745 -0.3598 -0.5206 -0.4383
0.0795
通过[F]=[K][δ]算出
NODE FX FY
1 -0.1318E+09 -0.4063E+09
2 -0.6762E+10 -0.1187E+10
3 0.1497E-03 -0.1928E+10
4 -0.1497E-03 0.1501E+10
5 0.000 0.1484E+10
6 0.9218E-04 0.1300E+09
7 0.1454E+10 -0.8880E+09
8 -0.1342E+11 0.2333E-04
9 -0.6164E+10 0.2260E-04
10 -0.3758E+09 0.000
11 -0.1569E+10 0.4939E-05
12 0.5202E+09 -0.7509E+09
13 0.000 -0.1185E+10
14 -0.3750E-05 -0.3567E+09
15 -0.7588E-04 -0.1050E+10
16 0.1486E-03 -0.1913E+10
17 -0.1318E+09 -0.4063E+09
18 -0.9653E+08 0.1296E+10
19 0.3825E+09 0.3080E+09
20 0.2709E+08 0.6057E+09
21 -0.7014E+09 -0.1994E+09
则σx的应力图
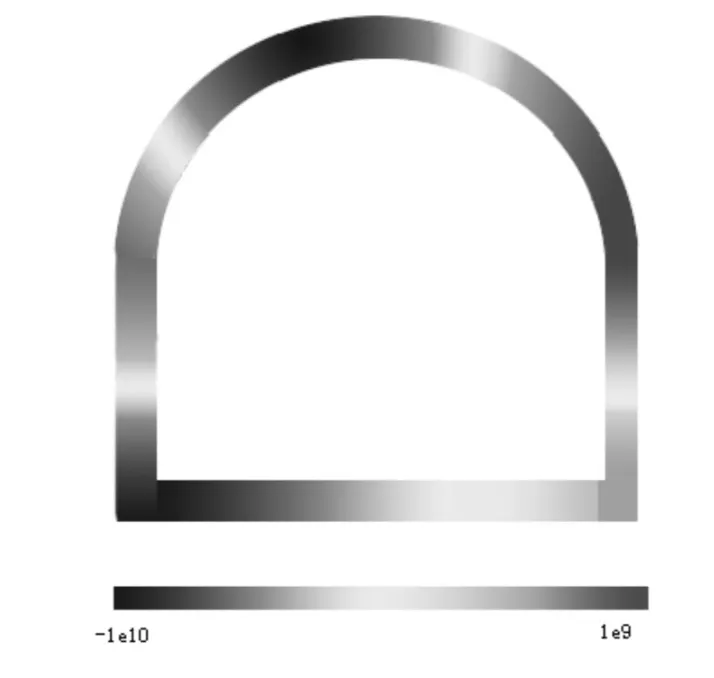
图5 σx应力图
则σy的应力图
从(18,19,20)可以看出右边受到压力,(17,21)点来看是受到拉力。可见结构出现了扭曲。
4 结论

图5 σy应力图
现在数学和计算机的发展迅速,我们从中受益良多。本文通过反分析法对隧道结构支护进行运算,分析了隧道的应力分布。粗劣的划分结构,只能起到定性分析的作用,而细致的划分就可以起到定性的作用,就可以对隧道支护提供依据。此外,位移反分析法还被应用于基坑工程、边坡、大坝等各个领域。近来岩土工程问题位移反分析方法的研究已取得了巨大进展,而且建立有较为系统的计算理论,而并用于实际工程问题分析。通过计算机进行位移反分析法分析其主要特点如下:1、直观性,计算机分析直观的反映了围岩的应力分布情况,反映了围岩的应变和位移;2、整体性,反映了整体的应力应变情况;3、准确性,对于粗劣的测量手段,较精确反映了应变的方向,应力的大小。可见计算机有限元结合位移反分析法直观准确的反映了工程状况,是一种实用而且有效的方法。
[1]钱鸣高,石平五.矿山压力与岩层控制[M].中国矿业大学出版社.2003,49-50.
[2]王长虹,杨有海.弹性位移反分析法在乌鞘岭隧道工程中的应用[J].兰州交通大学学报(自然科学版),2005,24(6).24-27.
[3]卢静涵,沈建虎,赵隆茂.反分析法在结构冲击动力响应实验中的应用[J].期爆炸与冲击,2004,24(2).140-144.
[4]李早,赵树德.基于可靠性理论的岩土工程反分析设计[J].西安建筑科技大学学报(自然科学版).2006,38(2),159-162.
[5]任高峰.基于位移反分析法的深凹边坡形状力学优化研究[D].湖北武汉,武汉理工大学.2005 1-15.
[6]郭艳华,郭志昆.岩土工程反分析的初步探讨[J],四川建筑科学研究,2006,32(3)105-108.
[7]蔡美峰,岩石力学与工程[M].北京科学出版社 .2002,284-301.
[8]武晓晖,宋宏伟.岩土工程反分析法的应用现状与发展[J]. 矿业工程 .2003,1(5),29-32.
